О влиянии относительного размера изображения на погрешность определения координат

Определение координат точечного источника света (ТИС) является одной из основных задач при определении положения объекта в пространстве. Для анализа положения светового источника широко используются фоточувствительные приемники матричной структуры, например, матрицы пространственно-зарядной связи (ПЗС).

Рассматрив аемая задача имеет важное прикладное значение. Если в качестве ТИС рассматривать звезды, то полученные результаты мог ут быть использованы для совершенствования оптико-электронных приборов звездной ориентации космических аппаратов [1]. Повышение точности определения положения звезд на каждом кадре позволит уменьшить общее время, требуемое для ориентации спутника в пространств е.

Проблема определения координат центра точечного источника света важна также и для фундаментальных исследований в астрономии. Работа [2] посвящена методам определения положения звезд, используемым при обработке информации, полученной с современных телескопов, в том числе и хаббловско-го. В работе описаны методы линейной и нелинейной фильтрации, применяемые для устранения шумов, оценки мощности сигнала, и даны конкретные рекомендации по их численной реализации. Оценку положения центра проекции предлагается осуществлять методом «центр тяжести». Другой подход, предложенный Микхелом (K. J. Mighell) в упомянутой работе, заключается в одновременной оценке всех параметров звездной проекции с помощью решения системы уравнения в частных производных и поиска оптимального решения нелинейным методом наименьших квадратов Левенберга-Маркара.

В работе [3] произведена оценка погрешности для метода центра тяжести для определения координат центра проекци и ТИС при наличии неравномерного фона и было произведено ее сравнение с неравенством Рао-Крамера. Кроме того, в данной статье построены зависимости погрешности опреде- ления координат от отношения сигнал/шум и размера скользящего окна.

В нашей стране данной проблематикой занимаются в СПбГУ ИТМО, что отражено в работах [4] и [5]. Авторами работы [4] предлагалось определять центр светового пятна с помощью сравнения реального сигнала с идеальным. В качестве модели идеального сигнала рассматривалась кривая Гаусса и квадрат Фурье-образа от апертуры. В работе [6] также предлагается определять центр изображения с помощью корреляционных методов и использовать в качестве эталонной гауссовскую функцию рассеяния. Для описания накопления заряда на матрице была принята пуассоновская модель. В качестве прикладного применения решаемой задачи указывается разработка методов топопривязки оптической системы по тестовым объектам.

Пуассоновская модель поведения индуцируемого на пикселях матрицы заряда использовалась в значительно более ранних работах. Так, в статье [7] автором была выведена функция правдоподобия для оценки координат центра проекции точечного источника света, энергетическая плотность которой распределена по закону Гаусса. В работе [8] приведена численная модификация метода максимального правдоподобия, предложенного в [7], позволяющая найти точку максимума ф ункции правдоподобия за меньшее количество итераций. К сожалению, автор статьи [7] ограничился в исследовании метода лишь оценкой Рао-Крамера, а результаты экспериментальных данных, приведенные в [8], трудно оценить, так как автор не нап исал, при каких характеристиках (размер пикселя, изображения, мощность сигнала и помех) было проведено моделирование.

Свет ТИС после прохождения через оптическую систему проецируется на плоскость анализа размытым пятном. Размеры и форма проекции зависят от оптической системы. Ошибка в определении координаты светового источника зависит от характеристик матрицы, параметров проецируемого изображения и от используемого алгоритма определения координат. На точность определения координат ока- зывают основное влияние следующие параметры проекции светового сигнала: мощность сигнала, функц ия распределения энергии сигнала, размер проекции изображения, время накопления сигнала, положение источника света относительно приемной структуры и интенсивность помех.

В работе [7] было показано, что при гауссовской форме сигнала наименьшая погрешность определения координат центра проекции ТИС достигается при значении радиуса рассеяния сигнала (РРС) порядка 0,6 размера элементарного фотоприемника (именуемого далее также пикселем или элементом дискретизации). При таких значениях РРС площадь проекции, на которую приходится большая часть мощности источника, составляет 1,5-2 площади элемента дискретизации. В работе [8] высказано другое предположение – наибольшая точность в определении координат достигается при размерах проекции, немного превышающих размеры пикселя.

Упомянутые предположения означают, что существует такой оптимальный радиус проекции, для которого дисперсия определения координат б удет минимальной, а любое уменьшение или ув еличени е размеров этого радиуса приводит к увеличению погрешности. Из этого следует, что усилия, направленные на дальнейшее совершенствование оптических систем, с целью уменьшения размеров проекции изображения, не п ривед ут к улучшению характеристик распознавания.

При получении оценки в работе [7] были сделаны сильные допущения, а именно:

• 1.    Использовалось свойство асимптотической эффективности оценки максимального правдоподобия (МП), что, однако, не верно для случая, когда радиус рассеяния мал и вся проекция размещается на одном или нескольких пикселях.

• 2.    При получении нижней границы дисперсии погрешности определения координаты предполагалось, что другая координата известна. Это предположение неверно, так как поиск минимума ф ункции правдоподобия осуществляется последовательным приближением по всем координатам.

Кроме того, зависимость погрешности определения координат от размера проекции была построена лишь для одного и весьма частного случая положения сигнала относительно приемной структуры . Указанные допущения не дают основания полагать, что реальные характеристики алгоритмов определения координат будут вести себя таким же образом, как и оценка, приведенная в [1].

Задача работы состоит в проверке гипотезы существования оптимального размера проекции . Для проверки этой гипотезы и нахождения оптимальных размеров РРС относительно размеров элемента дискретизации было проведено имитационное моделирование.

Методика и результаты моделирования

Модель основана на предположении, что фото-чувствительная матрица представляет собой совокупность прилегающих друг к другу пикселей без зазоров межд у ними. Геометрически плоскости матрицы соответствует область проекции изображения G (рис. 1). Область G разбита на прилагающие друг к другу непересекающиеся подобласти g ij прямоугольной формы, соответствующие пикселям матрицы.

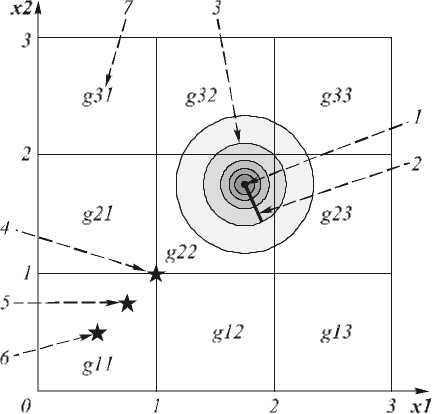
Рис. 1. Область проекции изображения G:

• 1    – центр проекции ТИС х0 , 2 – радиус рассеяния r,

3 – линии уровня мощности сигнала, 4, 5, 6 – положения центра проекции относительно приемной структуры, использовавшиеся при моделировании,

• 7    – подобласть g области G, соответствующая элементарному фотоприемнику

Энергия, накопленная каждым пикселем, измеряется количеством электронов, преобразуемых для цифровой обработки в кванты аналого-цифрового преобразователя (АЦП).

Модель построена исходя из предположения, что количество квантов АЦП с каждого элементарного фотоприемника ( i,j) есть случайная величина N ij . В [10] показано, что поведение этой величины может быть описано распределением Пуассона. То есть N ij ~ Po ( L ij ·t ), где L ij – интенсивность светового потока, падающего на пиксель ( i,j) , значение которой определяется выражением:

Li,j = IL (x) dx                                  (1)

gij

В выражении (1) L ( x ) = L1 ( x ) + l0 – двумерная пространственная ф ункц ия распределения интенсивности падающего на фотоприемник светового потока, x = ( x 1 , x 2 ) – координаты на приемной матрице, l0 – интенсивность помех ¹ на единицу площади, а L1 ( x ) – плотность энергии светового потока от полезного сигнала, равная

¹ Под помехами подразумеваются как собственные шумы матрицы, так и засветка от посторонних объектов.

L1 = J L1 ( x ) d x = const, G

• L 1 ( x ) = L1 • f ( x - x0 ) .                         (2)

В выражении (2) функция f ( x ) определяет пространственный характер распределения мощности энергии сигнала на проекции, x0 = ( x0 1 , x0 2 ) координаты проекции ТИС при прохождении лучей через идеальную оптическую систему. В модели предполагается, что мощность падающего на область G света от источника L1 не зависит от положения ТИС.

При прохождении света через оптическую систему в случ ае небольшого отклонения лучей от оптической оси пространственная плотность распределения энергии падающего сигнала с высокой степенью точности описывается нормальной кривой Гаусса. Поэтому в модели для исследования был принят след ующий вид ф ункции f ( x ):

exp (^{- (} x 1 + x 2 )/ 2 r ² )

f ( x ) = f ( x j , x 2 ) =---------— --------- ,       (3)

2n r где r – радиус рассеяния проекции.

Конечно, использование гауссоиды в качестве эталонной функц ии оправдано не всегда, поскольку в зависимости от свойств оптической системы плотность распределении эн ергии может в значительной степени отличаться от нормальной.

Однако для сложных оптических систем и случая немонохроматичного света плотность проекции ТИС будет иметь колоколообразную форму. Это обусловлено отчасти тем, что согласно центральной предельной теореме, сумма множества случайных слагаемых (к которым, с некоторой оговоркой, можно отнести отклонения луча от законов геометрической оптики на каждом этапе оптической системы) ведет себя как нормально распределенная случайная величина. Кроме того, если свет немоно-хроматичен, то дифракционные минимумы и максимумы лучей с различной длиной волны буд ут накладываться друг на друга, что, опять же, приведет к смазыванию классической дифракционной картины . Именно такой случай наблюдается в приборах звездной ориентации, где используется оптическая система, состоящая более чем из 10 линз, а звезды излучают свет в достаточно широком спектре.

Задача определения координат центра проекции ТИС заключается в след ующем - треб уется по совокупности данны х N оценить параметр х0 , считая параметры l0 и L1 известными.

При имитации накопления зарядов для каждого пикселя матрицы вычислялась, согласно (1), интенсивность падающего на него светового потока L ij . На этапе каждого вычислительного эксперимента для заданного времени накопления сигнала t генерировалась случайная реализация матрицы N . На основании каждой генерации матрицы N производилась оценка координаты центра проекции х0 .

После проведения серий экспериментов полученные значения оценок сравнивались с истинны м значением центра проекции х0, использованным при генерации матрицы N. По результатам этих сравнений вычислялись статистически е характеристики поведения ошибки определения координат.

При моделировании область G предполагалась состоящей из 225 подобластей g ij , что соответствует матрице размерности 15×15. Размер пикселя по горизонтали и вертикали считается одинаковым и принят за единицу измерений. Поскольку основная мощность сигнала сосредоточена в круге радиусом 3 r (рис. 1), то для определения координат центра проекции используется подобласть анализа размером 2 *kr +1. Радиус области анализа kr равен в используемых алгоритмах трем. За центр подобласти анализа (рис. 2) в обоих методах принимается пиксель ( i0, j0 ), имеющий максимальное значение заряда N i0, j0 .

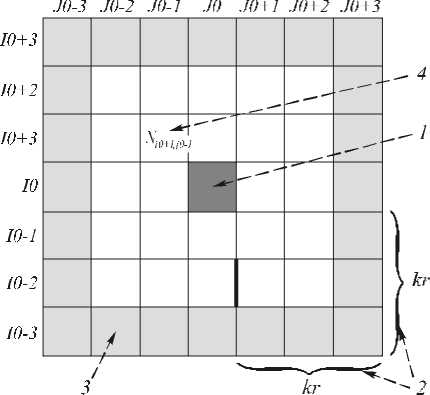
Рис. 2. Область анализа изображения.

• 1    – центр области анализа, 2 – радиус области анализа kr, 3 – граница области анализа,

4 – случайное значение заряда на пикселе

Для определения координат используются методы максимального правдоподобия (ММП) и «центр тяжести» (ЦТ). Оба алгоритма представляют собой два принципиально разных подхода к определению координат – алгоритм ММП предполагает априорное знание о форме и мощности сигнала и помех, а ЦТ не требует никакой дополнительной информации.

Используемая в работе оценка ММП основана на вычислении максимума ф ункции правдоподобия. Как показано в [7], для совокупности данных N плотности энергии (3) при оценке параметра х0 логарифм функ ции правдоподобия равен:

i0+kr j+kr

P(N| x0) = ^ ^ -t J L(x)dx + i=i0-kr j-kr

gij

+N i,j^ln t J ^L ( ^x ) d x ^-ln ( Ni J ! ) •

V gij 7

В правой части (4) не видна явная зависимость от х0 , но необходимо помнить, что согласно (2), функц ия L ( x ) зависит от оцениваемого параметра. За оценку х0 принимается то значение, при котором функц ия (4) достигает своего максимума (рис. 3).

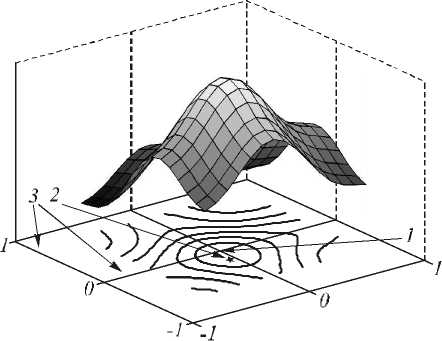
Рис. 3. Реализация функции правдоподобия.

Центр проекции находится в точке сопр икосновения пикселей: 1 – истинное положение центра проекции,

• 2    – оценка ММП положения центра проекции, 3 – граница области пикселя

При оценке координат методо м ЦТ исполь зо-валась оценка фона, принимаемая равной среднему значению зарядов пикселей, находя щихся на границе подоб ласти анализа (рис. 2). Величины заряд а N уменьшаются на в елич ину оценки фона. Для оценки координат используются знач ения N , превысившие заданный по рог и соприкасающиеся сторонами или углами . Если в случайной реализации N все значения оказываются меньше заданного порог а, то такая реализация не используется для оценки коорд инат. Оценка коорд ин ат методо м ЦТ осуществляется на основании выражений, приведенных в [2].

При моделировании были приняты следующие значения параметров L1 = 100 квантов АЦП / с, l0 = 20 квантов АЦП / пиксель·с . Время накопления t = 20 мс. Такие значения сигнала и шумов соответ-ств уют случаю проекции звезды блеском 5 – 6 m на фоне собственных шумов матрицы.

В работе были исследованы характеристики алгоритмов для рад иуса r, варьировавшегося от 0,2 до 0,8 размера элемента дискретизации с шагом 0,1. Были рассмотрены три различных случая положения центра проекц ии (рис. 1): в центре пикселя – точка 6, в точке соприкосновения пикселей – точка 4, и в точке, находящейся посередине отрезка межд у двумя предыдущими – точка 5. Первы е два положения проекции относительно приемной структуры соответствуют, как было показано в [9], случ аю максимального и минимального отношения сигнал/шум. Наиболее информативным, с точки зрения поведения характеристик алгоритмов в среднем, является случай положения ц ентра, соответствующий точке 5.

Согласно [2] оценка дисперсии погрешности определения координат центра проекции х0 методом МП составляет:

Г                                    221 -1

I L1²t_v rd f ( x - ^x0 )

Dx01 = l-^ J     —dx r .     (5)

• l^{0 i,j} L gij    d x^{0 1}        J

  Результаты моделирования представлены на рис. 4, 5, 6, где изображены графики зависимости среднеквадратичного отклонения (СКО) определения координат центра проекци и (в % от раз мера пикселя) от относительных размеров r . Графики построены для трех характеристик: ошибки ММП, ошибки метода ЦТ и оценки (5). Графики построены на основании статистических данных, полученных в результате генерации не менее чем 3000 экспериментов (по каждой точке), что гарантирует ошибку в определении СКО, не превышающую 1%.

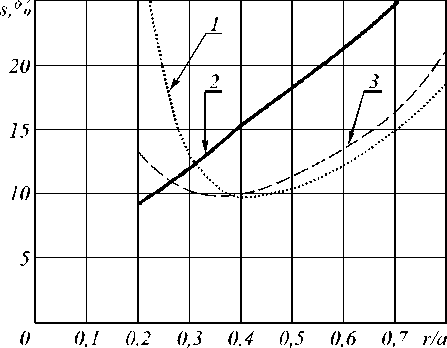
Рис. 4. Зависимость СКО определения координат от величины радиуса рассеяния. 1 – СКО координат, полученных ММП, 2 – СКО координат, полученных методом ЦТ, 3 – оценка СКО координат, основанная на неравенстве Рао-Крамера

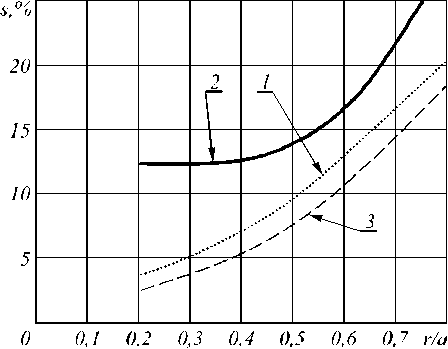
Рис. 5 Зависимость СКО определения координат от величины радиуса рассеяния:

1 – СКО координат полученных ММП,

2 – СКО координат полученных методом ЦТ,

3 – оценка СКО координат, основанная на неравенстве Рао-Крамера

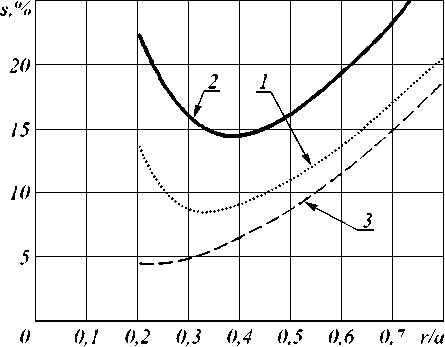
Рис. 6. Зависимость СКО определения координат от величины радиуса рассеяния:

• 1    – СКО координат полученных ММП, 2 – СКО координат полученных методом ЦТ, 3 – оценка СКО координат, основанная на неравенстве Рао-Крамера

Результаты проведенных экспериментов позволяют сделать следующие выводы. Как видно из графиков, на зависимость ошибки определения координат от РРС проекции заметное влияние оказывает как положение центра проекции, так и используемый для определения координат алгоритм. В общем случае, оценка МП, как и следовало ожидать, обладает меньшей погрешностью, нежели оценка методом ЦТ.

Исключение составляет вырожденный случ ай, когда центр проекции совпадает с центром элементарного фотоприемника (рис. 4). При малом радиусе проекции алгоритм ЦТ всегда б удет вычислять координаты проекции, совпадающие с координатами центра пикселя, в какую бы часть его области они не попали. Когда координата проекции совпадает с центром пикселя, то погрешность определения координат стремится к нулю (кривая 2 на рис. 4), при уменьшении РРС. Однако стоит отметить, что характеристики алгоритма «центр тяжести» в значительной степени зависят от выбора порога обнаружения. Так, аппроксимация графика зависимости СКО от РРС показывает, что при уменьшении радиуса СКО б удет стремиться не к 0, а к некой положительной константе (около 9% в рассматриваемом случае). Эта ошибка об условлена тем, что иногда заряды пикселей, индуцируемые шумовой составляющей, превосходят порог обнаружения.

В остальных случаях погрешность определения координат методом ЦТ превышает ММП в среднем почти вдвое.

В среднем, минимум дисперсии достигается при отношении РРС к размеру пикселя 0,3 – 0,4. Однако при приближении центра проекции к центру элементарного фотоприемника точка минимума для графика (кривая 2 на рис. 1) ошибки ЦТ постепенно смещается к нулю, и U-образная кривая вырождается в прямую. При расположении центра проекции вблизи точки соприкосновения пикселей (рис. 5) также не наблюдается экстремума ф унк ции, и по- грешность обоих методов монотонно возрастает при ув еличении РРС.

Оценка ошибки ММП, предложенная в [7], меньше ошибки ММП на 10-15% при r > 0,4 и может на этом полуинтервале использоваться для оценок погрешности. Для малых РРС величина нижней границы заметно отличается от погрешности ММП, а характер ее поведения не соответствует реальным характеристикам алгоритма. Столь заметная разница между теоретическими и реальными характеристиками алгоритма при малых РРС объясняется фактами, упомянутыми в начале данной статьи.

СКО метода ЦТ составляет в среднем 20±5%. Это значение соответствует прив еденной в [9] оценке, утверждающей, что СКО метода ЦТ приближенно равно размеру пикселя, деленному на отношение сигнал/шум.

Заключение

Согласно полученным результатам оптимальный размер радиуса рассеяния для определения координат центра проекции ТИС составляет 0,3 – 0,35 от размеров элементарного фотоприемника, что почти вдвое меньше оценки, данной в работе [1].

На основании полученных результатов моделирования можно сделать вывод, что уменьшение радиуса рассеяния проекции ТИС в полтора-два раза, по сравнению с используемым в современных оптико-электронных приборах зв ездной ориентации, позволит уменьшить погрешность определения координат центра проекци и звезд на 15-20%. Для работающих в реальном времени приборов звездной ориентации уменьшение погрешности определения координат позволит уменьшить время определения положения спутника в пространстве за счет сокращения затрат на селекцию помех типа «светящаяся частица» и получению более точных зн ачений о межзвездных углах.