О влиянии переменного магнитного поля на диэлектрические свойства полупроводника

О ВЛИЯНИИ ПЕРЕМЕННОГО МАГНИТНОГО ПОЛЯ НА ДИЭЛЕКТРИЧЕСКИЕ СВОЙСТВА ПОЛУПРОВОДНИКА

Проблемы перестройки параметров излучения и перспективы создания управляемых дифракционных решеток привлекают внимание к вопросу о свойствах полупроводниковой плазмы в переменных внешних полях [1*3]- В данной работе решается задача определения усредненной диэлектрической проницаемости е плазмы в быстроме-няющемся магнитном поле Н. При этом будем считать, что эффективная длительность свободного пробега Т не зависит от времени. Последнее справедливо, если связанное с Н внешнее электрическое поле Евнеш много меньше характерного "плазменного11. В противном случае частота внешнего поля должна быть достаточно велика, чтобы т не успевало его отслеживать, т.е. зависело лишь от амплитуды Евнеш (подробнее см. [)])• г ? -icot

Уравнение движения заряда в поле волны Е = Ео • е с несущей частотой со имеет традиционный вид:

m*«(^Y + vv) = е-(Е + [V * в]),                                           (1)

где * ш - эффективная масса; е - заряд электрона; v - средняя скорость; V - эффективная частота столкновений;

8 = u0-H(R,t) - внешнее магнитное поле.

Формально при интегрировании (1) следует учесть зависимость Т от координат R/ т.к. V = R. Однако масштаб изменения В будем считать макроскопическим, а масштаб колебаний R под действием Е - микроскопический ^тах " еЕ0/(т-ыа)), так что в дальнейшем зависимость Н от координат будем учитывать параметрически.

Пусть Н = (Но ♦ H^cos Qt)-hz где h - безразмерный вектор (|h| = h - 1). Введем плотность тока J = е-N-v, где N - концентрация носителей;

le|.u0

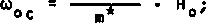
1е|-цо to. ~ ---т-- • Н - циклотронные частоты постоянной и переменной части поля

1 с1

соответственно.

Тогда для J получим

^ * V. J + (шос + <01С • cos nt) • [j х h] = ^ Eo • e‘wt.(2)

Положим, не нарушая общности, что Н (в отличие от [)]) имеет двухкомпонентную структуру h = (0, hyZ hz).

Выделяя из (2) периодическую часть решения 7 = о • ?о • е 1Wtz следует отметить, что тензор проводимости О зависит от времени посредством набора гармо-ikQt ,                    ,                             ,« ник ~е с убывающими по к коэффициентами. Усредняя О по периоду 2п/П, получим

-    г а =    - ia h /Ь ср     I - z

\ та h /h

- У

ia_ hz/h о0+(а+ - a0)h2/h2 (а0 - a+)hyhz/h2

- тс h /К - У

(а0 - a+)hyhz/ha а0+(о+ - a0)ha/h2

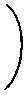
где о+ определяются функциями Бесселя Int

" о Ы1 г

=  ^t"^-^

т Ne’/m*    _ _ , Ne2

о = —:—:— » о = 1.

О to + TV +2m*

_____________________1______________________, + _____________________1

ш + ш. -h + пП + iv ~ to - со - nQ + tv ос

Корректность усреднения О по времени становится очевидной в случае Q « to, что обязывает произвести в (3) и С¹») предельный переход. Игнорирование этого обстоятельства приводит в [,] к сомнительному выводу о заметных изменениях резонансных соотношений, обусловленных переменной составляющей Н₁. Учет Q « ш дает особенно наглядные результаты при отсутствии постоянной составляющей H_Q. Тогда среднее по периоду 2п/П значение магнитного поля равно нулю, и плазма в среднем остается изотропной. Действительно, при to_QC = 0 из (к) имеем а_ = 0. Тогда из (3) ясно, что в s-поляризованной волне Е * (Е_х,0,0) компоненты J_{y z} не появятся (аналогично для p-поля ризации не появится J_x)-Конкретизируем полученные результаты в случае s-поля ризации: J = J_y⁼ J- ⁼ 0- Тогда для диэлектрической проницаемости е = 1 + —12— _из ^{7      4}                                                                          е -о

(3) и (А)

с учетом свойств Бесселевых функций при П « ш имеем: .                          Я2

е = е + де, ё = 1 - —,—-л. , , G) (G) + 1V) *

“л’^с’Ь2                 1,2 * q2>

2to« (to * iv)3              (о) + iv)2

где лэнгмюровская частота плазмы.

Рассмотрим один из конкретных способов возбуждения переменного магнитного поля в полупроводниковой плазме. Пусть полупроводниковая пластина пронизана системой токов J = J1 • cos fit, параллельных ее поверхности и коммутируемых по направлению (рис. 1). При этом создаваемое такой системой поле Н будет иметь вид:

J • cos nt

И = ——$—:----- • К(а,и), где а = L/l, и = у/1,

I

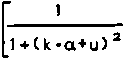
1+(к-а-и)

и      ”       (к-а-и)       (к'а+и)

----- * 2 5 ,   -------------; * -------------Г

1+и3   к = 1     [1+(к-а-и)     1+(к-а+и)

Здесь $к = 1 для сонаправленных токов; s^ = (-1) для токов чередующихся направлений. Выражение (7) предполагает бесконечное количество токов. Влияние со ответствующих краевых эффектов при необходимости нетрудно учесть, ограничив в

I еI'Uo J 1

• ( 7) пределы суммирования. Для перехода к (5) следует подставить со = ----— • -р

• 3 .52 -10 (4) • ^ •

  

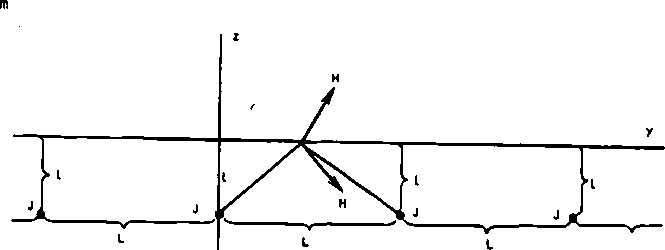
  Рис. 1. Схема расположения токов

  
  

„ m J (А)                                                                 2пт

возбуждающих магнитное поле

Реальный интерес в проблемах создания управляемых дифракционных решеток представляют периодические неоднородности в Де [2]. Далее будем рассматривать лишь продольную неоднородность (вдоль оси у), полагая, что для z < 0 излучение поглощается на длине много меньшей, чем I. Оставим в Де из (5)лишь первое сла гаемое (что справедливо при Wi(_ « [у + ivl и ограничимся в разложении перио дического ha(y) из (7) одной гармоникой, положив ha(y) - ( max min)i

,h2    ~ h2- I max min

* I-------2-------I

(f = h ~ h . ; E maxmin'

2ny _ ' . Тогда

= Ttl/L) :

для периодической части Де(у)

получим

Де (у)

П„ы3 f (Е)

Л 1 с

4у • (y+iv) 3

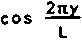
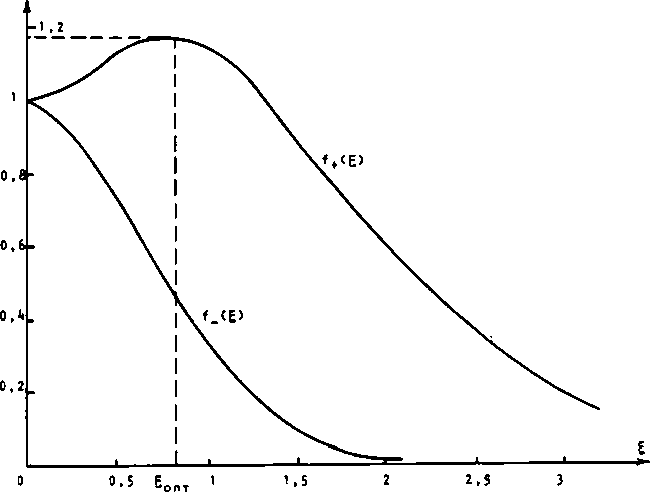
где для сонаправленных токов f+(Е) = Ea-

а для токов чередующихся направлений:

*-<Е1 - <тНё>’-                                                      "°>

Соответствующие зависимости изображены на рис. 2. При этом max(f^) = 1,17 достигается для (1/L)    = 0,256.

опт

Рис. 2. Зависимости (9), (10), характеризующие амплитуду переменной части Де в (8)