О влиянии подземных горных выработок на инженерно-геологические условия Прикамья

Наличие заброшенных рудников на территории Пермского края является одним из факторов, усугубляющих условия строительства. Активизация ряда экзогенных процессов (в частности, суффозии) осложняют инженерно-геологическую обстановку и требуют особого внимания.

История появления подземных горных выработок связана с началом освоения территории Прикамья с целью добычи меди. Первые медные руды промышленного значения здесь были открыты в 1635 г. у Григоровой горы на берегу р. Камы (р-н Боровска). В начале XVIII в. Петром I была начата активная выплавка меди на Урале.

Сырьевой базой медеплавильного производства Пермских заводов на всем протяжении их истории являлись медистые песчаники шешминского горизонта. Они тянутся в виде двух полос шириной до 100 км с севера на юг на расстояние более 1500 км (рис. 1).

Рудные тела не представляют единого выдержанного на большой площади горизонта. Они встречаются в виде разобщенных линз и гнезд неправильной, чаще вытянутой формы. Длина их колеблется от 60 до 200 м.

В отдельных случаях, снижаясь до 20 м и увеличиваясь до 2 км, обычная ширина рудных тел 10–20 м, редко достигает 150 м.

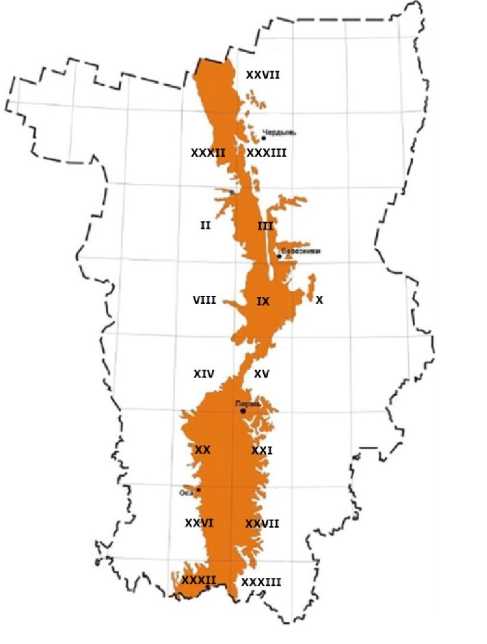
Рис. 1. Полоса выходов меденосной шешминской свиты в пределах Пермского края (римские цифры - номенклатура планшетов листа Р-40 и О-40 масштаба 1:200 000)

Мощность медистых линз колеблется от 0,1 м до 2 м, в исключительных случаях достигая 6 м. Глубина залегания от нескольких

метров у бортов речных долин до 80 м на водоразделах. Рудные тела располагаются на нескольких гипсометрических уровнях. Известно до шести рудных горизонтов между-камерных целиков в рамках ортотропной среды.

Сложная конфигурация расположения подземных выработок требует понимания их роли при оценке инженерно-геологических условий, а главное, в каждом случае принимать рациональные конструктивные решения. Это тем более важно, что количество установленных выработок на территории Перми составляет -507 (рис. 2). Практика строительства в подобных условиях показывает, что при определенных условиях (прежде всего, воздействии поверхностных стоков и грунтовых вод) присутствие подземных выработок является фактором, провоцирующим деформации зданий и сооружений.

Это подтверждается фактическим материалом. В особенности крупные аварии наблюдались в районе Мотовилихи, где интенсивность разработок была наибольшей в связи с возникновением медеплавильных заводов. Достаточно вспомнить обрушение подъезда жилого дома по ул. Крупской 37, провал трамвайных путей на ул. Крупской, аварийные ситуации с домами по ул. Лебедева, ул. Ким и ряде других.

В этой связи в подобных районах принята практика бурения скважин на глубины не менее 30–40 м, учитывая вероятность расположения подземных выработок на указанных глубинах.

Глубина залегания выработок во многом определяла и конструкцию фундамента. При наличии выработок на относительно небольших глубинах (до 10–20 м) применяются, главным образом, висячие сваи. Однако

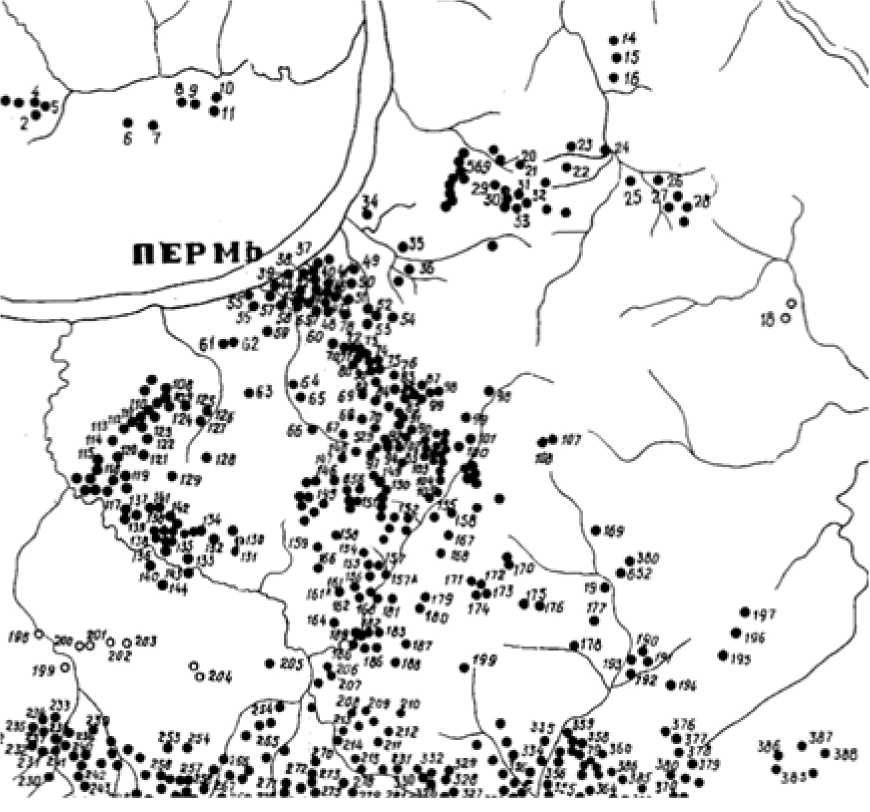
Рис. 2. Карта медных рудников XVIII – XIX вв. Пермских медеплавильных заводов

практика показывает, что при длительной эксплуатации сооружений несущая способность основания в дисперсных грунтах существенно понижается в силу уменьшения сил сцепления, что связано с активизацией процессов суффозии. Висячие сваи при этом уже не выполняют свою функцию.

Решение проблемы необходимо искать в возможности использования в качестве основания коренных пород независимо от наличия подземных горных выработок. Главной задачей при этом является определение несущей способности кровли выработки в зависимости от нагрузки сооружения, глубины заложения сваи-стойки и прочностных характеристик коренных пород в каждом конкретном случае.

Диапазон физико-механических свойств песчаников достаточно широк и определяется характером цементации. По этому признаку ранее была проведена типизация коренных пород красноцветной терригенной формации (Гайнанов, Трусова, 2019, 2020). Анализ свойств песчаников показывает, что даже самые слабые разности в состоянии нести необходимую нагрузку при использовании их в качестве основания

В данной статье на основе расчетной модели предложена возможность использования в качестве основания коренных пород с учетом глубины залегания выработок, нагрузки на их кровлю и прочностных характеристик.

Расчетная схема задачи

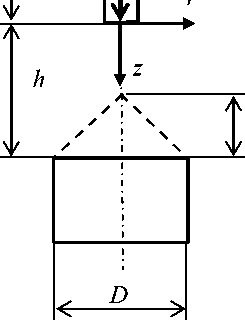
Рассмотрим одиночную сваю (рис. 3), опирающуюся на однородный грунт с заданными механическими свойствами. Расстояние от опоры (основания) сваи до поверхности грунта - Н , расстояние от основания сваи до кровли цилиндрической полости - h , диаметр цилиндрической полости - D , нагрузка на сваю - Р , средний удельный вес грунта - Y .

Напряженное состояние грунта в окрестности кровли полости складывается из горного давления, определяемого величиной Y (Н + h ), и полем напряжений, индуцированным действием сваи на опору.

Для оценки поля напряжений воспользуемся решением упругой задачи Буссинеска

(Тимошенко, Гудьер, 1975) о действии сосредоточенной силы на границе полупространства. Согласно решению, вертикальные (осевые), радиальные и окружные напряжения определяются выражениями:

° z = 3- z ³ f ^-5/2 ,     (1)

2ll

Р                 „          _¹

От = --{(1 - 2v)r 2(1 -zf 2) -

3zr ² f^-},

ое = - £ (1 - 2v){r-2 (-1 + zf-) + zf—2}, где r, z - цилиндрические координаты, отсчитываемые от основания сваи (рис. 3); f = r2 + z2; v - коэффициент Пуассона.

Земная поверхность

H

P

h к

Рис. 3 Расчетная схема

Отметим, что в выражении (1) знак «плюс», согласно принятым в геомеханике и механике грунтов правилам для напряжений, соответствует сжатию.

На рис. 4 показаны кривые распределения вертикального напряжения az по радиусу r для двух значений глубин (расстояния по вертикали от опоры сваи - точки приложения нагрузки): кривая 1 - 3 м, 2 - 4 м. Очевидно, что максимальное напряжение быстро затухает с глубиной, обратно пропорционально квадрату глубины.

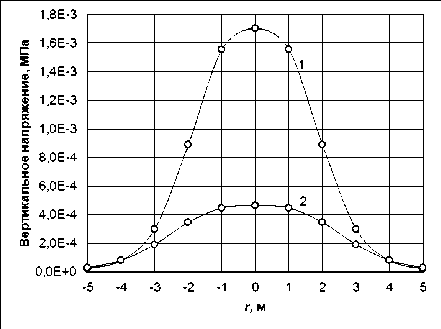
Рис. 4. Распределение вертикальных напряжений по радиусу для двух значений глубины

Будем в качестве средней оценки уровня напряжений от действия сваи на глубине z принимать максимальное значение интенсивности напряжений Т (Тимошенко, Гудьер, 1975), достигаемое при r = 0 (на оси сваи)

T = ^^^O t -oOe-      (2)

Кроме напряжений (1), вызываемых действием внешнего усилия на сваю, в грунте действуют еще и напряжения, определяемые собственным весом пород. На глубине расположения кровли полости Н+ h напряжения от горного давления равны ozr = Y(fl + h),

y = О д = Ау(Н + h), (3)

где А = ^; ^_ коэффициент бокового распора.

Напряжения от горного давления (3) должны суммироваться с напряжениями от нагрузки на сваю (1) при оценке потери устойчивости пород над полостью (выработкой).

Соотношения (1)–(3) справедливы для однородного полупространства. Если на глубине h от опоры сваи расположена некоторая полость, то вблизи нее напряженное состояние искажается, взаимодействуя со свобод- ными границами (прежде всего с кровлей) полости.

Оценка искаженного вида напряженного состояния является достаточно сложной задачей. Согласно геомеханическим представлениям (Методическое руководство по ведению горных работ на рудниках ОАО «Сильвинит», 2011), при действии горного давления вблизи кровли полости возникает коническая (в первом приближении) область – так называемый свод естественного равновесия – по которой и может произойти разрушение кровли полости. Возможность разрушения определяется механическими характеристиками, прежде всего параметрами сцепления с и углом внутреннего трения φ , входящим в предельное соотношение Кулона-Мора (Цитович, 1983).

Высота конической области hк, согласно оценкам (Методическое руководство по ведению горных работ на рудниках ОАО «Сильвинит», 2011), равна hк = 0,7 D. (4)

Нам необходимо оценить предельное расстояние между опорой сваи и кровлей полости, при котором не возникает разрушение породы и просадки сваи.

Для максимального упрощения инженерной оценки предельной глубины сваи примем, что поле суммарных напряжений (1) и (3) может вызвать разрушение кровли полости, если на уровне глубины вершины конической области над кровлей полости интенсивность напряжений (2) достигает значения предела прочности на срез, определяемого сцеплением грунта с и углом внутреннего трения φ.

Ниже используется предельное условие Друкера-Прагера (Друкер, Прагер, 1952), являющееся обобщением условия Кулона-Мора на пространственный случай:

T(z = zj < (с + ptg(p)/n (5)

р = (or + og + oz)/3, где p – гидростатическое давление; n – коэффициент запаса прочности.

Подставляя выражения (1)–(3) в неравенство (5), окончательно получим нелинейное неравенство для оценки допустимого значения z * , через которое с учетом (4) определяется искомая величина h * = z * + 0,7D

• -^-■Ь^У^"^-)* -

• - ^—^ (irM^   (6)

Из неравенства (6) следует, что предельное расстояние h * нелинейным образом зависит от всей совокупности основных параметров задачи.

Рассмотрим конкретный пример применения полученного выражения (6) для случая одиночной сваи и одиночной полости: D = 3 м; Н + h ср = 25 м; Р = 80 т = 0,8 МН; γ = 2,5 г/см³ = 0,025 МН/ м³; λ = 0,7; n = 5.

В расчетах принимали различную величину сцепления грунта с = (1,3–4) МПа и два значения угла внутреннего трения φ = 10° и φ = 20°.

На рис. 5 показана зависимость предельного расстояния h * от величины сцепления грунта. Сплошная линия соответствует значению φ = 20°, пунктирная – φ = 10°.

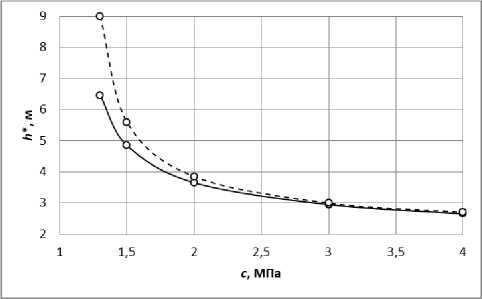
Рис. 5. Расчетная зависимость предельной величины h*

Таким образом, разработана инженерная методика оценки предельного расстояния между опорой сваи и кровлей полости, выполненная для простейшего случая одиночной сваи и одиночной цилиндрической полости, соосной свае.

Вариант расположения одиночной сваи над протяженной выработкой является более опасным, чем рассмотренный в статье.

При наличии нескольких свай (групп свай) и/или протяженных выработок получение подобных инженерных оценок является затруднительным. В этом случае необходимо применять методы математического моделирования в 2D или 3D постановке.

Однако результаты, полученные при расчете для одиночной сваи, позволяют принципиально изменить подход по выбору конструктивных решений для фундаментов в условиях присутствия в основании горных выработок. При наличии информации по прочным характеристикам коренных пород, ожидаемой нагрузки от сооружения и глубины расположения выработки можно рассчитать глубину заложения сваи-стойки. Эта конструкция позволяет исключить вероятность негативного воздействия возможных экзогенных процессов в вышележащих дисперсных грунтах. В частности, процессов суффозии грунтов мелких фракций.