О влиянии слабых электрических воздействий на релаксацию механических напряжений в алюминии

Одним из основных требований, предъявляемым к деталям ответственного назначения, является стабильность их размеров и формы в течение всего срока эксплуатации. Причина отклонений от задаваемых параметров – пластическая деформация, которая в конечном счете приводит к разрушению детали. Распространенным видом пластической деформации в технике является релаксация напряжений, которая, с одной стороны, может привести к ослаблению механических соединений, с другой стороны, релаксацию напряжений нужно стимулировать для снятия остаточных напряжений. Поэтому необходима разработка способов управления этим видом пластической деформации с помощью внешних энергетических воздействий, но для этого нужно знать характер и общую кинетику протекания пластической деформации в условиях данных воздействий.

Большие успехи достигнуты в изучении влияния внешних электрических воздействий, в частности импульсного токового [18] и воздействия электростатическими полями большой напряженности. Последнее хорошо изучено в твердых диэлектриках [6]. К настоящему времени установлено, что внешние электрические воздействия существенно меняют дислокационную субструктуру материала. Так, в [19] показано, что при воздействии электрических потенциалов степень самоорганизации дислокационной субструктуры в разрушенных при испытании на ползучесть образцах изменяется. Однако изменение дислокационной субструктуры в случае релаксации напряжений в условиях слабых электрических воздействий практически не изучалось.

Цель настоящей работы – провести анализ изменения дислокационной субструктуры в процессе релаксации механических напряжений алюминия при наложении электрического потенциала.

Исследования выполнены на цилиндрических образцах технически чистого алюминия А 85, диметром 22 мм и высотой 16 мм. Образцы были предварительно отожжены в течение двух часов при температуре 773 К для снятия внутренних напряжений. Для нагружения образцов (испытание на сжатие) использовалась деформационная машина с автоматической регистрацией усилий во времени. Процесс релаксации механических напряжений начинался после прекращения нагружения при σ 0 = 57 ± 0,5 МПа и скорости деформиро-

вания 0,002 с-1. Как и в [8], [9], на образец накладывался электрический потенциал с диапазоном изменения от -1,5 до +1,5 В.

Полученные в эксперименте релаксационные кривые аналогично [3], [19] использовались для определения основных характеристик релаксации механических напряжений. К этим характеристикам относятся активационный объем γ и коэффициент чувствительности скорости пластической деформации к изменению внешнего напряжения m = d ln( - σ & ) d ln σ . В качестве количественных характеристик влияния электрического потенциала ϕ использовались относительное изменение активационного объема ζ = ( γ ϕ - γ 0 ) / γ 0 и коэффициента чувствительности скорости пластической деформации к изменению внешнего напряжения ξ = ( m _ϕ - m 0 ) / m 0 , где γ _ϕ и m _ϕ – значения соответствующих величин для ненулевого потенциала, а γ 0 , m 0 – для нулевого.

Из стандартных кривых σ (t) [1] определялись зависимости глубины релаксации Δσ от времени (рис. 1). Видно, что при наложении потенциала релаксация напряжений ускоряется. При t ≈ 400 с процесс релаксации замедляется и глубина релаксации напряжений принимает следующие значения:

Δσ 1 м (400 с) ≈ 5,1 МПа для ϕ = 0 В;

Δσ 2 (400 с) ≈ 8 МПа для ϕ = -1 В;

Δσ 3 (400 с) ≈ 9,5 МПа для ϕ = 1 В.

Полный временной интервал измерений равен t = 0 с ÷ 1500 с, и для этого момента времени соответствующие значения равны

Δσ 1 (1500 с) ≈ 11 МПа;

Δσ 2 (1500 с) ≈ 12,5 МПа;

Δσ 3 (1500 с) ≈ 15 МПа.

В целом глубина релаксации не превышает 15 МПа. На всем временном интервале измерений для ϕ = 1 В δ = [ Δ σ 3 -Δ σ 1 ] ≈ 4 МПа, причем и этот эксперимент, и последующие (для активационных параметров) обнаруживают независимость результатов измерений от знака приложенного потенциала.

Результаты вычисления активационного объема и коэффициента чувствительности скорости пластической деформации к изменению внешнего напряжения при различных значениях потенциала представлены в таблице.

Изменения γ и m не зависят от знака электрического потенциала и отражают общую тенденцию их снижения с ростом потенциала ϕ .

Полученные результаты, по-видимому, могут быть интерпретированы с помощью представлений о поверхностной энергии и коэффициенте поверхностного натяжения алюминия [10]. Рост поверхностной энергии под воздействием потенциала может быть связан, на наш взгляд, не только с образованием двойного электрического слоя [4], но и с движением дислокаций в поверхностном слое образца в процессе релаксации напряжений. То, что важным для понимания физики явления должна быть картина эволюции движущихся дислокаций, следует из факта ускорения

Изменение параметров γ и m под воздействием электрического потенциала

φ, В	-1	-0,5	0	0,5	1
γ, 10-27 м3	1,35	1,29	1,7	1,41	1,27
m	10,7	13,0	14,4	11,3	10,6

Примечание . γ – активационный объем, m – коэффициент чувствительности скорости пластической деформации к изменению внешнего напряжения.

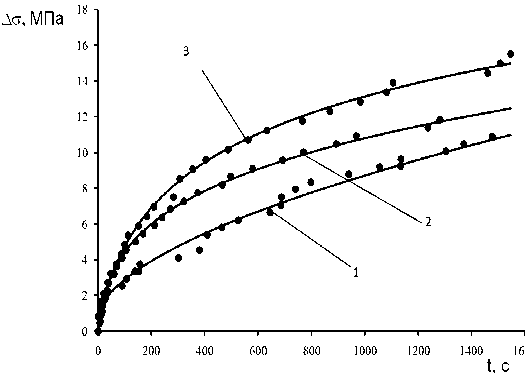
Рис. 1. Изменение глубины релаксации от времени испытания в обычных условиях (кривая 1), при потенциале поверхности -1 В (кривая 2) и +1 В (кривая 3)

релаксации напряжений. Ограничимся рассмотрением поведения дислокаций в условиях одноосной модели пластической деформации, предложенной в [5]. Используем традиционный подход к описанию пластической деформации [5], основанный на синтезе идей физической [2] и математической теории пластичности [7], [17]. Можно предположить, что активационный объем γ уменьшается с ростом потенциала потому, что подвижные дислокации закрепляются в процессе релаксации напряжений, а на закрепленные дислокации электрический потенциал не влияет через механизм роста поверхностной энергии. Воспользуемся синергетическим подходом к роли подвижных дислокаций, вихревому характеру пластической деформации (уровень зерна) и структурным уровням пластичности [12], [13].

Поскольку пластическая деформация алюминия осуществляется при относительно низких температурах, не превышающих 0,5 Tm (Tm – температура плавления), она реализуется за счет дислокационного скольжения, причем дислокации преодолевают препятствия термофлуктуационным образом. Из выражения для активационного объема γ = bld [15], [16], где b – вектор Бюргерса, l – длина дислокационной петли, d – поперечный размер локального стопора, полагая d ≈ b, получим выражение l ≈ γ /b2. Значение активационного объема для нулевого потенциала γ(0) = 1,7 ⋅ 10-27 м3, значение вектора Бюргерса для алюминия b = 2,86 Å [16], откуда l ≈ 21 нм. Если роль центров закрепления играют дислокации «леса», то мы можем оценить по порядку величины соответствующую плотность дислокаций ρ ≈ l-2 ≈ 2,3 ⋅ 1015 м-2. Столь высокие значения плотности дислокаций могут свидетельствовать о наличии развитой сетчатой дислокационной структуры [14]. Высокая плотность закрепленных дислокаций и незначительное число подвижных дислокаций приводят к тому, что при наложении потенциала из-за наличия более высокой поверхностной энергии подвижные дислокации при релаксации закрепляются медленнее, чем при нулевом потенциале. А поскольку активационный объем определяется числом закрепленных дислокаций, при ненулевом потенциале он меньше, чем при нулевом (в согласии с рис. 2). Коэффициент m ведет себя аналогичным образом, так как с ростом потенциала снижается работа по преодолению дислокацией препятствий [19].

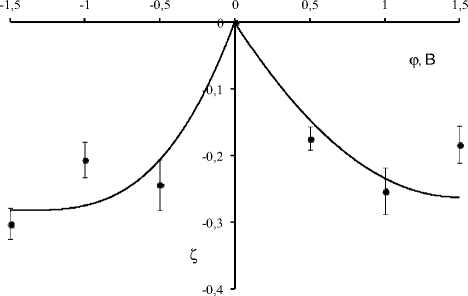
Рис. 2. Зависимость относительного изменения активационного объема от электрического потенциала

Воспользуемся физико-математической моделью одноосного растяжения (сжатия) [5] применительно к нашей задаче. Для жесткопластической среды модель включает следующие уравнения [5]:

d ρ s

=ρν -ρν

ggs ssg dt

ν sg = ν 0 exp

U - < 7/ / n ^ kT ^J ,

(1а)

(1б)

(1в)

(1г)

•            •

ε = ε 0 exp

U - Y7 / n ^ kT ^J ,

где ρs , ρg – плотности закрепленных и подвижных дислокаций, vgs – частота превращений подвижных дислокаций в закрепленные, νsg – частота превращений закрепленных дислокаций в подвижные (преодоление барьеров и т. п.), t – время, ν0 – предэкспоненциальный множитель, U – энергия активации процессов преодоления барьеров (средняя), σ – внешние (внутренние) напряжения, k – постоянная Больцмана, Т – термодинамическая температура, γ – активационный объем, n – фактор Тейлора для поликристалла (для хаотической разориентировки зерен n = 2,8 ÷ 3,1), b – усредненный по системам скольжения вектор Бюргерса, υ – средняя скорость подвижных дислокаций, ε – пластическая деформация.

Уравнение (1а) является уравнением «баланса» подвижных и закрепленных дислокаций, уравнение (1б) – это уравнение для кинетической константы реакции исчезновения закрепленных дислокций в форме С. Аррениуса, уравнение (1в) – известное в физике пластической деформации [16] уравнение Орована, уравнение (1г) представляет собой активационный закон типа С. Аррениуса для пластической деформации.

Подставляя в (1г) энергию активации U = βGb³ , где β – коэффициент, принимающий значения от 0,38 до 0,45 для разных металлов, активационный объем γ = b 2 / ρ S , ν 0 = ν D b ρ S ,частоту Дебая ν D = 10¹² c^-1 и предэкспоненциальный множитель ε & = ε & * b ρ s , ε & * ≅ ν D , получаем решение уравнений для одноосного сжатия. Оно имеет вид формулы для напряжения течения для случая ε & = const, Т = const.

σ=βnGb 1+ln ρs , (2) ( eGb3 e*b4 ps J где G – модуль сдвига (для алюминия 27 ГПа [13]).

В соответствии с общепринятыми представлениями, первое слагаемое в (2), получающееся после раскрытия скобок, является атермической компонентой напряжений, а второе – термической компонентой. Формулу (2) можно применить к оценкам изменения плотности дислокаций ρ S , добавив поправку на внешний потенциал и поверхностную энергию к начальным напряжениям релаксации. Из формулы (1г) следует, что рост внутренних напряжений, обусловленных внешним потенциалом, ведет к снижению скорости деформации ε, что в соответствии с формулой (2) приводит к увеличению начального напряжения течения материала. Рост напряжения течения, согласно рис. 1, выражается в увеличении глубины релаксации Δσ для потенциала ϕ = 1 В. Качественно зависимость σ ( ρ S ) ~ ρ s от плотности закрепленных дислокаций в начальный момент релаксации справедлива и для вклада поверхностной энергии в напряжения. Изменение поверхностной энергии под воздействием потенциала, в свою очередь, связано с подвижными дислокациями.

Таким образом, установлен эффект влияния электрических потенциалов на релаксацию механических напряжений технически чистого алюминия А 85. Выдвинуто предположение о том, что увеличение глубины релаксации обусловлено изменением поверхностной энергии и дислокационной структурой.

Работа выполнена при финансовой поддержке ФЦП «Научные и научно-педагогические кадры инновационной России на 2009–2013 гг.» (гос. контракт № П411).