О влиянии температурных деформаций упругих элементов на динамику движения космического аппарата

ется воздействию высоких и низких температур. Помимо колебаний после срабатывания УРД, большие упругие элементы под влиянием существенно неравномерного поля температур скачкообразно меняют свою форму, размеры и физические свойства. Это явление сродни своеобразному ударному воздействию, передаваемому на корпус КА. С одной стороны, существенное влияние температурного градиента на физические свойства требует отдельных исследований масштабов этого влияния на поле микроускорений, порождаемое за счет колебаний больших упругих элементов КА, с другой, - ударное воздействие приводит к появлению дополнительных микроускорений, величину которых необходимо оценить. Причем, такой эффект характерен для всех упругих элементов КА, не зависимо от их способностей колебаться.

Проекты современных космических лабораторий, таких как “ОКА-Т” предусматривают уровень микроускорений, согласно проектным данным, не должен превышать 10 мкм/с2 [11]. Поэтому задача исследования и оценки микроускорений, создаваемых за счет градиента температур упругими элементами КА, является актуальной.

В работе производится оценочный расчет микроускорений, возникающих при температурных деформациях стержневого упругого элемента. Это исследование, с одной стороны, позволит учесть влияние на поле микроускорений таких упругих конструктивных элементов, как антенна, с другой, - послужит основой для более сложной модели температурных деформаций рамы, которую представляют собой панели солнечных батарей и радиатора.

Рассмотрим уравнение теплопроводности [12]: k V T+B=gT ,            (1)

где κ - теплопроводность; В – тепловыделение в объеме; с – теплоемкость на единицу объема.

Граничные условия

TIO₁ = T , кд n T IO₂ = q .

Здесь заданы температура и внешний тепловой поток. Для оценочных расчетов достаточно полагать, что поток q пропорционален разности температур окружающей среды и тела. В этом случае справедливо условие третьего рода:

кдnT + k(T - 7]) = 0 ;

при бесконечно большом коэффициенте теплообмена k приходим к условию первого рода T = T , а при k ^ 0 -- к условию теплоизоляции д _nT = 0 .

Недостатком (1) является его неволновой характер и бесконечно большая скорость распространение тепла. Уравнение волнового (гиперболического) типа получится при усложненном выражении вектора потока тепла h :

0 h + h = - KV T .          (2)

Здесь 0 - постоянная времени установления теплового потока; h реагирует на изменение V T с запаздыванием. Тогда уравнение:

- divh + B = cT при соотношении (2) приводит к гиперболическому уравнению:

KV T + B + 0B = C (T + 0 T ) ;

Причем, скорость распространения тепла равна 7 к I c 0 .

Для получения приближенной оценки воспользуемся моделью однородного стержня длины l и теплоизоляцией боковой поверхности. Начальное температурное распределение выбрано в соответствие с условиями теплового удара, что учитывает реальные особенности прогрева больших упругих элементов КА. Поскольку при прогревании температура на концах стержня будет меняться, граничные условия имеют подвижный характер:

д T ₂ д ² T — = a —7, dt д x

где a = —, p - плотность, с - удельная теп- лоемкость, X — коэффициент теплопроводности.

В случае решаемой задачи граничные условия и начальное температурное распределение запишутся следующим образом:

T ( o , t ) = A i (t ), T ( I , t ) = ^( t ), 0 <  t <+ю ,

T ( x , 0) = ф ( x ), 0 <  x <  I , где ф (x ) - функция, соответствующая условиям теплового удара. Она выбиралась в соответствие с кубической гранецентрированной структурой решетки алюминия с параметром 4,050 . 10^-4 м [13].

Согласно методу Фурье, решение (3) примет следующий вид:

T (x, t) = u (x, t) + v (x, t), где u

⁽ x, t ) = Ц _х ⁽ t ) + у [ ^ 2 ⁽ t ) ^- А ⁽ t ) ] ,

ю

v(x, t)=Е Cne n =1

1 2

I а ² 1

. nn sin — x, l ^,

-I

C n = ?J ф ( ^ ) ^sin т .

/ 0 t

Сделаем две оценки времени прогрева для случая штатного режима работы больших упругих элементов, под которыми в данной ситуации будем подразумевать панели солнечных батарей (ПСБ), когда косинус угла между нормалью к ПСБ и направлением на Солнце должен быть не менее 0,9 [11]. Вторая оценка касается максимального времени прогрева больших упругих элементов, под которыми в данной ситуации будем подразумевать панель радиатора и любой другой элемент, для которого косинус угла между нормалью и направлением на Солнце должен быть близок к нулю.

Считая Солнце ламбертовским источником, рассчитаем величину падающего теплового потока, приходящегося на упругий элемент:

где

Ф

Ф =- П п 4 п ’

Φ - полный поток энергии от Солнца,

S

Q = —^ cos а - телесный угол, R - расстояние от Солнца до Земли.

Численное моделирование времени полного прогрева в пакете Mathcad дало результаты, представленные на рис. 1 и 2.

На рис. 1 кривая 1 представляет собой начальное распределение температур ф ( x ), о которой говорилось выше. Далее эпюра выравнивается с течением времени и превращается в горизонтальную прямую 7, что свидетельствует о равномерном прогреве ПСБ. Линии 1, 2, 3, 4, 5, 6 и 7 соответствуют моментам времени 0; 0,005 с; 0,01 с; 0,05 с; 0,1 с; 0,5 с и 1,6 с соответственно. Таким образом, можно утверждать, что оценка времени полного прогрева ПСБ будет следующей:

J t = 1,6 с . (4)

На рис. 2 аналогично рис. 1 кривая 1 представляет собой начальное распределение температур ф ( x ), а линии 1, 2, 3, 4, 5, 6, 7 и 8 соответствуют моментам времени 0; 2 ч 46 м 40 с (10⁴ с); 13 ч 53 м 20 с (5?10⁴ с); 27 ч 46 м 40 с (10⁵ с); 3 сут 9 ч 20 м 00 с (3?10⁵ с); 5 сут 18 ч 53 м 20 с (5?10⁵ с); 11 сут 13 ч 46 м 40 с (10⁶ с) и 35 сут 9 ч 18 м 52 с. Причем, последнее время является временем полного прогрева семиметрового радиатора через его торец.

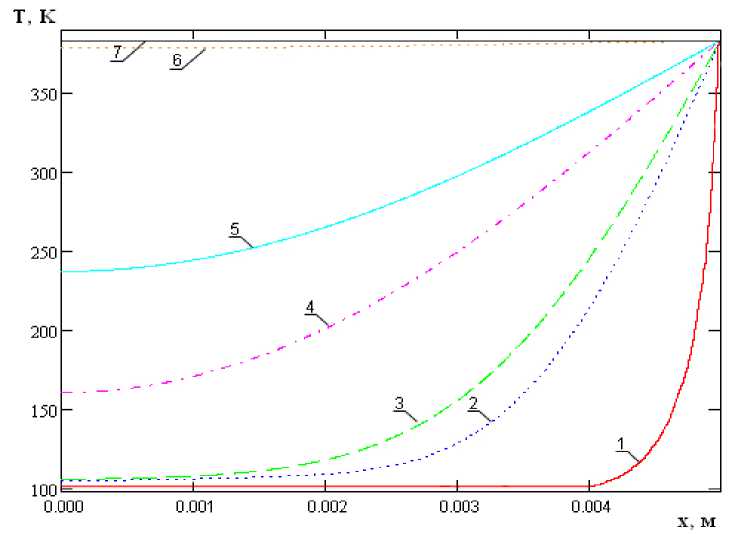
Рис. 1. Эпюра распределения температуры внутри ПСБ в случае их штатной работы

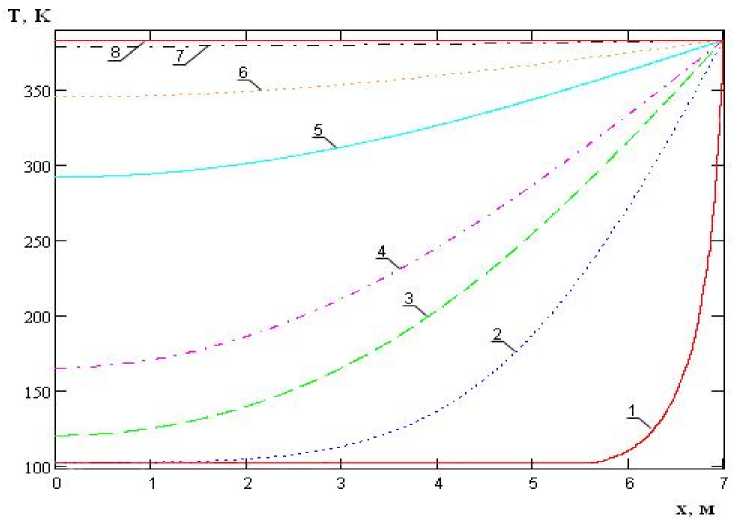
Рис. 2. Эпюра распределения температуры внутри панели радиатора

Прогрев настолько незначителен, что в большинстве практических задач им можно пренебречь. Данная оценка времени завышена из-за неучета излучения тепла упругим элементом с одной стороны, с другой, – за столь продолжительный отрезок времени КА успеет неоднократно побывать в тени и выйти из нее. Другое дело, что эта оценка получена в расчете пренебрежимо малого отличия угла между нормалью к панели и направлением на Солнце от 90о, т.е. прогрев осуществлялся только за счет тепла, проходящего через торцевое сечение элемента. Вопрос о влиянии на время полного прогрева нарушений этих идеальных условий, например за счет колебаний упругого элемента, является темой отдельного исследования и в данной работе не рассматривался.

Рассмотрим далее какого порядка возмущения могут быть вызваны при температурных деформациях ПСБ для космической лаборатории типа “Ника-Т” (проектные параметры приведены в [11]), используя оценку (4). Приращение импульса ПСБ за счет ее деформации оказывается приблизительно равным 2,2 кг м/с. При ус- ловии, что весь импульс без потерь будет передан корпусу КА можно оценить модуль создаваемых микроускорений:

w= Δp ≈ 2 ⋅10-4 м/с2 m0 ⋅ Δt

.

Оценка (5), несомненно, завышена, поскольку приращение импульса будет рассеиваться, а не полностью передаваться на корпус. Колебания ПСБ приведут к тому, что часть импульса будет затрачено на деформацию и т.д. Однако, с другой стороны, следует заметить, что требования по микроускорениям в проекте “Ника-Т” составляли не более 2 ⋅ 10 ^-5 м / с ² , что на порядок ниже оценки (5).

Таким образом, проведенные исследования позволяют сделать вывод об актуальности проблемы влияния температурных деформаций на динамику движения КА, если речь идет о специализированных КА технологического назначения, на которых предполагается проводить длительные по времени гравитационно-чувствительные технологические процессы. Без проведения подобных оценок невозможно утвеждать о выполнении условий микрогравитационного штиля во время проведения процессов, если КА периодически оказывается в тени и выходит из нее.

С другой стороны, необходимо использование более сложной математической модели теплопроводности, а также передачи импульса на корпус КА в сочетании с рассмотрением реальных форм больших упругих элементов для существенного уточнения оценки (5) и формирования рекомендаций по минимизации неблагоприятного влияния выявленного эффекта на поле микроускорений внутренней среды КА.

Данная работа представлена на Самарский областной конкурс “Молодой ученый” – 2010.