О влиянии точности арифметических расчетов на результаты молекулярно-динамического эксперимента

Метод молекулярной динамики (МД) является одним из наиболее распространенных вычислительных методов, применяемых для моделирования атомных и молекулярных систем. Суть метода МД состоит в численном решении уравнений движения с использованием ЭВМ [8], [9], [10]:

dr m— = p, dt

dpt = ^ F <  ' )' dt i * i

В совокупности с начальными положениями и скоростями частиц эти уравнения представляют собой задачу Коши, для решения которой наиболее часто используется алгоритм Верле [4]:

' " + 1 = ' " + v n -A t + 0,5 - a , . ( a t ) ²,

• П + 1 n I A C. ( П + 1 I n \ A

• v , = v , + 0,5 - ( a , + a , ) - A t.

Значение ускорения i-й частицы получается из второго закона Ньютона a , = F , ( t ) / m , где m -масса частицы, а F (t) – суммарная сила, действующая на i-ю частицу со стороны остальных. Сила взаимодействия между частицами вычисляется из потенциала межчастичного взаимодействия по формуле f_y = - gradU ( т_у ) .

Результатами проведения МД-эксперимента являются координаты и скорости частиц моде © Крупянский Д. С., Фофанов А. Д., 2015

лируемого кластера на каждом временном шаге, а также значения потенциальной и кинетической энергии. Особый интерес для исследования структуры материала представляет равновесная конфигурация атомов, получаемая после завершения эксперимента.

При моделировании системы, состоящей из N частиц, для решения каждого уравнения необходимо рассчитать N (N-1) /2 парных взаимодействий, то есть временные затраты на проведение МД-эксперимента растут пропорционально квадрату количества частиц в системе и для достаточно больших систем могут оказаться неприемлемо высокими.

Одним из наиболее доступных способов сокращения времени моделирования является применение графических процессоров (ГП) для параллельного расчета парных взаимодействий [1], [2], [6]. Использование ГП позволяет получать значительный прирост производительности [3] даже на недорогих моделях графических ускорителей. При этом необходимо помнить об архитектурных особенностях этих вычислительных устройств, таких как падение производительности вычислений при использовании двойной точности.

При проведении расчетов на центральном процессоре (ЦП) ощутимой разницы временных затрат при использовании одинарной (single precision) и двойной (double precision) точности не обнаруживается. Поэтому вопрос об использовании одинарной точности в МД-расчетах оставался неактуальным. Однако расчеты с двойной точностью на ГП проводятся в несколько раз медленнее, чем с одинарной. Авторами [5], [6], [12], [14] приводятся данные, свидетельствующие о 2–8-кратном падении производительности при выполнении double-операций на современных графических ускорителях.

В настоящей статье приведены результаты исследования о возможности использования арифметики с одинарной точностью для расчетов методом молекулярной динамики.

МЕТОДИКА ИССЛЕДОВАНИЯ

Для оценки степени влияния точности вычислений на результаты молекулярно-динамического расчета был проведен ряд экспериментов с различными условиями и стартовыми конфигурациями. Объектами исследований являлись наноразмерные кластеры, состоящие из: оксида кремния в аморфном и кристаллическом состоянии, оксида магния, оксида кобальта, а также легированные кобальтом ксерогели жидкого стекла. При использовании одинарной точности в некоторых экспериментах наблюдались изменения структуры моделируемых объектов, отсутствующие в аналогичных экспериментах, проведенных с двойной точностью. Наилучшим образом такие изменения видны в экспериментах, моделирующих фазовый переход со сменой полиморфной модификации или с изменением степени упорядоченности (кристаллизация). При моделировании неупорядоченных структур влияние точности вычислений на поведение структуры атомных кластеров не выявлено из-за сложностей численного описания таких структур. Наблюдаемое в экспериментах появление структурных различий связано с ошибками округления [13], [15], являющимися общей проблемой расчетов с плавающей запятой, не связанной с конкретным типом вычислительных устройств [11].

Влияние точности расчетов на результаты моделирования продемонстрировано на примере наиболее показательного эксперимента, в ходе которого происходит кристаллизация модельного кластера. Результаты экспериментов, полученные с разной точностью, сравнивались с помощью методики, описанной в статье [7] ( http://mmp.vestnik . susu.ac.ru/pdf/v7n2st4.pdf). Также в настоящей статье приводятся соответствующие кривые потенциальной энергии, отражающие изменения в структуре моделируемого объекта.

ОПИСАНИЕ ЭКСПЕРИМЕНТА

Стартовая конфигурация представляла собой кластер, имеющий форму куба со стороной 35Å и состоящий из 1000 случайно распределенных по объему атомов кислорода и магния в равном стехиометрическом соотношении. Единственное

ограничение, накладываемое на взаимное расположение частиц, заключается в том, что расстояние между двумя атомами не должно быть меньше 1,5Å. В расчетах использовался потенциал в форме Борна – Майера – Хиггинза:

^qi^q j^e 0 ²

Uij= r ij

(

+ A_ij exp

-

Г rij

-

V

p j

C ij r ⁶ ij

Исследуемый кластер помещался в центр модельного объема в виде куба со стороной 150Å, что было в несколько раз больше размеров исходного атомного кластера. Таким образом, поверхность кластера могла принимать энергетически наиболее выгодную форму. Во всех модельных экспериментах радиус обрезания потенциалов был равен 70Å, что позволило учесть взаимодействие каждого атома со всеми остальными атомами моделируемой системы. Один временной шаг соответствовал 10–15с модельного времени, всего было рассчитано 100 000 шагов. В ходе эксперимента происходило зарождение центров кристаллизации с дальнейшим ростом новой фазы по всему объему кластера.

Моделирование проводилось с использованием параллельной реализации метода молекулярной динамики для графического процессора NVIDIA [6] ( http://elibrary.ru/item.asp?id=20318865 ) с одинарной и двойной точностью на следующей конфигурации:

Процессор:     Intel Core i7–3770L 3500 МГц

ОЗУ:          8096 Гб DDR3–2133

Видеокарта:   2ГБ GeForce GTX 660, com pute capability 3.0

Компиляторы: g++ 4.6.3, nvcc 5.0

Библиотеки: cuda runtime, libquadmath, igraph c library 0.7.1

Полученные результаты были проверены с помощью реализации МД для процессора с архитектурой x86 с четверной точностью (библиотека gcc libquadmath) при прочих равных условиях.

РЕЗУЛЬТАТЫ

В ходе МД-эксперимента, проведенного с двойной точностью, образуется упорядоченный кластер, имеющий правильную решетку типа NaCl (две ГЦК-подрешетки из катионов и анионов, сдвинутых друг относительно друга на половину телесной диагонали элементарной ячейки) (рис. 1а). При проведении расчетов с одинарной точностью полученный в результате эксперимента кластер представляет собой агрегат из мелких кристаллитов, сросшихся друг с другом под разными углами (рис. 1б). В данном случае более низкая точность расчета влечет за собой потерю вклада удаленных частиц при расчете сил взаимодействия, что негативно сказывается на общей упорядоченности структуры модельного кластера.

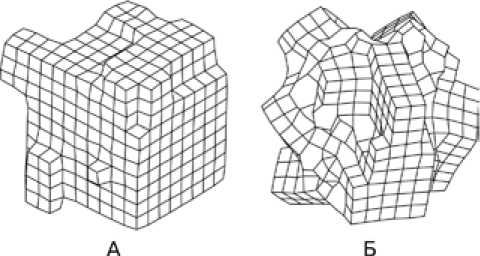
Рис. 1. Схематичное изображение структуры модельного кластера, полученного при расчетах с двойной (а) и одинарной (б) точностью

На рис. 2 представлен график изменения потенциальной энергии модельного кластера в ходе экспериментов с одинарной и двойной точностью. Первые 3000 шагов модельного времени кривые полностью совпадают. В момент времени t = 3000 на графике заметно незначительное расхождение кривых, после которого они снова практически совпадают.

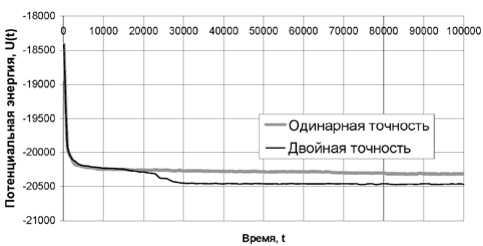
Рис. 2. Графики изменения потенциальной энергии при расчетах с разной точностью

Значительное расхождение кривых начинается после 20 000 шагов МД-эксперимента. Величина потенциальной энергии при моделировании с одинарной точностью продолжает равномерно убывать вплоть до окончания эксперимента, а более резкое снижение значений этого параметра при расчете с двойной точностью свидетельс- твует о существенных изменениях в структуре моделируемого объекта – кристаллизации.

К моменту времени t = 20000 структуры кластеров, полученных с различной точностью, практически неразличимы – оба кластера содержат некоторое количество упорядоченных областей (зародыши кристаллизации). Далее, при использовании двойной точности вычислений один из зародышей становится центром кристаллизации всего кластера. Атомы, окружающие эту область, начинают упорядочиваться, происходит фазовый переход. Так как в расчете сил учитываются взаимодействия каждой частицы со всеми остальными, суммарный вклад удаленных частиц является значимой величиной. Поэтому зародыши, не ставшие центром кристаллизации, под действием силы со стороны уже упорядоченных атомов естественным образом встраиваются в растущую структуру. При использовании одинарной точности вклад одной частицы, расположенной на достаточном расстоянии, может оказаться настолько малым, что будет потерян при округлении. Таким образом, частицы, расположенные на противоположных концах кластера, практически не взаимодействуют друг с другом. В этом случае с момента времени t = 20000 каждый зародыш начинает формировать собственный центр кристаллизации. Близкие центры, взаимодействующие друг с другом, срастаются в один кристаллит, а более дальние срастаются «неправильно», то есть разориентированы друг относительно друга.

Графики на рис. 2 отражают качественные различия в течение процесса моделирования, обусловленные исключительно различной точностью выполнения расчетов. Для более детального анализа этих различий было проведено исследование структурных изменений моделируемого кластера в соответствии с методикой, изложенной в [7]. На каждом шаге МД-эксперимента был построен граф g, описывающий структуру модельного кластера. Вершинам графа g соответствуют найденные в кластере магний-кислородные октаэдры, ребро соединяет две вершины, если соответствующие им многогранники имеют

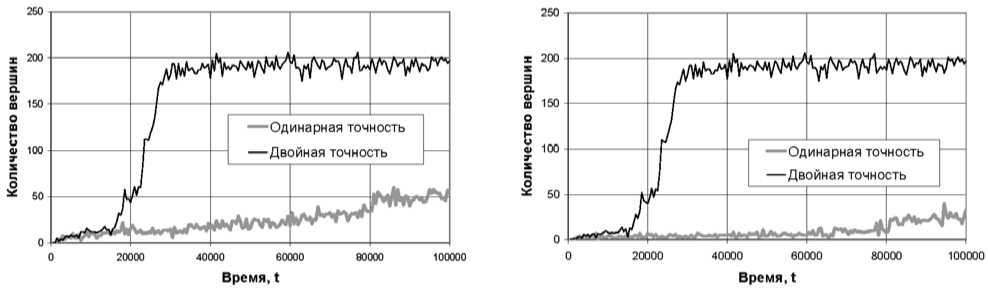
Рис. 3. Графики изменения порядка графа g (слева) и его гигантской компоненты (справа)

общее ребро. Затем с помощью библиотеки igraph был рассчитан порядок гигантской компоненты связности этого графа – инвариант, чувствительный к процессам изменения структуры кластера, происходящим при кристаллизации.

Результаты расчетов инвариантов графа g для одинарной и двойной точности приведены на рис. 3. При расчете с двойной точностью кривые порядка графа g и порядка его гигантской компоненты практически совпадают. Это говорит о том, что в большинстве случаев каждая новая вершина графа g присоединяется к гигантской компоненте. На кривых хорошо виден резкий подъем, соответствующий процессу фазового перехода. Рост кристалла в этом случае происходит из одного центра кристаллизации. При расчете с одинарной точностью порядок графа g растет без значительных скачков, при этом порядок гигантской компоненты этого графа осциллирует около некоторого постоянного значения вплоть до момента времени t = 60000. Таким образом, гигантская компонента в этом случае не формируется. За 80 000 шагов модельного времени образуется около десятка связных компонент, имеющих порядок от 1 до 10 вершин, которые за последние 20 000 шагов эксперимента срастаются в две. Рост кристалла происходит из нескольких центров кристаллизации. Образовавшиеся кристаллиты срастаются под различными углами.

По графикам потенциальной энергии, представленным на рис. 2, можно было бы сделать вывод об адекватности данных, полученных с одинарной точностью за первые 15 000–20 000 шагов модельного времени. Однако графики на рис. 3 свидетельствуют о накоплении заметной ошибки уже за первые 10 000–15 000 шагов.

ВЫВОДЫ

Проведено множество молекулярно-динамических экспериментов с одинарной и двойной точностью арифметических расчетов для нано-размерных кластеров на основе оксида кремния, оксида магния и оксида кобальта. Результаты большинства проведенных вычислительных экспериментов качественно соответствуют результатам эксперимента, описанного в настоящей работе. Собранные данные свидетельствуют о критическом влиянии точности выполнения расчетов на конечную структуру моделируемых атомных кластеров.

На примере кристаллизации кластера на основе оксида магния показано, что использование одинарной точности в молекулярно-динамических расчетах приводит к потере вклада удаленных частиц при расчете сил межатомного взаимодействия, что выражается в снижении степени упорядоченности структуры моделируемого объекта. При моделировании неупорядоченных кластеров выявить различия в ходе экспериментов, проводимых с различной точностью, не удалось в силу сложности численного сравнения структуры этих кластеров.

Результаты всех вычислительных экспериментов, проведенных с двойной точностью, соответствуют результатам аналогичных экспериментов, проведенных с четверной точностью с использованием библиотеки gcc libquadmath. Следовательно, двойную точность для данной задачи и схемы интегрирования можно считать достаточной. Использование одинарной точности расчета может качественно изменить ход вычислительного эксперимента и не может быть оправдано приростом производительности, получаемой на таких вычислительных устройствах, как графические процессоры.

* Работа выполнена при поддержке Программы стратегического развития ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012–2016 гг.

IMPACT OF ARITHMETIC PRECISION ON RESEARCH RESULTS

OF MOLECULAR-DYNAMIC SIMULATION