В практике научного приборостроения могут найти весьма полезное применение такие физические явления, как самофокусировка оптических (электромагнитных) пучков и самовоздействие акустических пучков в нелинейной акустике (содержание этих терминов раскрывается ниже). В настоящем обзоре речь пойдет о самовоздейст-вии акустических пучков в нелинейной акустике.

В 1962 г. в работе [1], по-видимому, впервые было предсказано явление самофокусировки (электромагнитной) волны, вызванное возмущением свойств среды в области локализации волны по сравнению со свойствами невозмущенной среды. В работах [2, 3] было дано теоретическое обоснование возможности самофокусировки волновых пучков в соответствующих нелинейных оптических и плазменных средах. В работе [4] это явление наблюдалось экспериментально. В основе оптического явления самофокусировки пучков лежит возможность взаимной компенсации дифракционной расходимости и нелинейной рефракции. Это же характерно и для самофокусировки акустических волновых пучков. Самофокусировка таким образом вследствие антагонистичного взаимодействия нелинейной рефракции и дифракционной расходимости проявляется в том, что пучок под ее воздействием обладает малой пространственной расходимостью, что позволяет сохранять высокую фокусировку энергии, близкую к изначальной.

Пионерская работа [5], в которой приближенным уравнением нелинейной акустики ограниченных пучков (позднее названным уравнением Хох- лова—Заболоцкой (УХЗ)) описывается математическая модель распространения ограниченных пучков в нелинейных средах без потерь, послужила мощным толчком к интенсивному изучению этой проблематики. В настоящее время насчитываются десятки работ, посвященных изучению методов решения и нахождения асимптотик принципиально нелинейного уравнения, каковым является УХЗ.

Наряду с УХЗ, справедливым для идеальных, нетеплопроводных сред, вскоре в работе [6] было получено уравнение, названное позже уравнением Хохлова—Заболоцкой—Кузнецова (УХЗК), пригодное для вязких теплопроводящих сред.

ВОЛНОВЫЕ ПУЧКИ

Согласно [7, с. 321] суперпозиция плоских волн с близкими по направлениям волновыми векторами может дать локализованное в поперечном направлении поле — волновой пучок с почти плоским волновым фронтом. Причем поперечные размеры пучка d значительно превышают длину волны λ , но малы по сравнению с длиной пучка. Величина d ограничена снизу пространственным соотношением неопределенности А к ■ d >  п , где А к — поперечный разброс волновых векторов, характеризуемый углом а = А к/к , ( к = 2 п / X ). При а ^ 1 (малоугольное приближение) kd » 1. Такие пучки можно считать нерасходящимися d ²

на расстояниях R < — .

λ

УРАВНЕНИЕ ХОХЛОВА—ЗАБОЛОЦКОЙ

В русскоязычной литературе уравнение Хохлова—Заболоцкой (см., например, [5, 8, 9]) приведено первоначально в работе [5], хотя в аэродинамике околозвуковых потоков это уравнение было получено значительно раньше в [10]. Изложение вывода уравнения приведем, основываясь на работах [5, 8, 11]. Уравнение получено при следующих предположениях.

1. В качестве исходной модели движения жидкости принимается система уравнений Эйлера, описывающих распространение возмущений конечной амплитуды в идеальной жидкости без затухания (см., например, [8, с. 10]):

• 2.    Рассматриваются ограниченные пучки, распространяющиеся в слабонелинейных средах.

• 3.    Поскольку пучок полагается квазиплоской волной, распространяющейся вдоль оси Ox , то по аналогии со случаем плоских волн конечной амплитуды (см., например, [8, гл. 2]) решение ищется в виде следующего анзаца [5], [8, с. 225]:

Vx , P ' P = * t

V

—

—, ЦХ, ТУу, ^pz I c 0                  J

отражающее тот факт, что изменения всех величин поперек пучка происходят быстрее, чем вдоль

пучка. Параметр

принятия анзаца

µ определен ниже; при условии ¥(•••) справедливы оценки [9,

( дv          I P — + (vV) v =—Vp, (дt        J (1) др + V( Pv ) = 0, (2) p = p (P). (3) с.

^{д р   д} v x

---~-- дx' дx'

~

~

µ 2 ;

д р д р д v _x д v _x д p ' д p ' ------------

д у '    д z '

д у '    д z '    д у '    д z '

µ 3/2

.

Система (1)–(3) является полной и состоит из законов сохранения импульса (1) и массы (2), а также уравнения состояния (3). Уравнение состояния для газа предполагается адиабатическим [8, с. 10]:

Поперечные обусловленные порядок малости

компоненты скорости, расходимостью пучка, имеют

µ 3/2

[8, с. 226], [9, с. 17]

v y

~

γ

— = — I ,              (4)

P о V Po J cp где y = —, cp, cV — удельные теплоемкости cV при постоянном давлении и объеме соответственно; p0 и ρ0 — равновесные давление и плотность газа. Уравнение состояния для жидкостей, носящее название уравнения Тэта, — также в форме (4)

~

v _z

~

~

µ 3/2

.

4. Уравнение Хохлова—Заболоцкой выводится с точностью до O ( Ц ² ) .

Фигурирующий выше безразмерный параметр µ определяется следующим образом [5, 8]:

p

* ^p

( Ar

P I

I P o J ’

где эмпирические параметры Г u p * для различных жидкостей табулированы, например, в [12, с. 166, 167] (величину p ^* называют внутренним

давлением, параметр Г характеризует отклонение жидкости от закона Гука [12, с. 162] и формально определяется так: Г = 1 +--0 [8, с. 10], c — др c2

скорость звука). Таким образом, уравнения состояния для газов и жидкости имеют одинаковый

вид, различаясь только двумя входящими в них параметрами.

v x ρ ' p '

µ , c ₀ ρ ₀ p ₀

где c ₀ — скорость распространения слабого сигнала (скорость звука в приближении линейной акустики); v — вектор скорости жидкости; ρ ₀ , ρ ' соответственно равновесное и возмущенное значения плотности жидкости (газа); p ₀ — равновесное давление для газа и p ₀ = p * для жидкости. Величина p ' для жидкости определяется так [8, с. 225]:

p ' = c о² р '+ ( Г — 1 ) c о² р '²/2 Р о .

После принятия обозначений

x

• т = t --; x = цx ;

c ₀

• у ' = Цуу ;      z ' = V pz

и несложных преобразований исходной системы (1)–(3) в работах [5], [8, с. 227], [9, с. 19] для величины ρ ' получено уравнение Хохлова— Заболоцкой

(18)), а в случае уравнения для v _x это будет коэффициент ρ ⁰ .

c ₀

а д ² р² 2 д т¹

д ² р д x д т

+ c ⁰ А₂ р = 0, 2²

УРАВНЕНИЕ

ХОХЛОВА—ЗАБОЛОЦКОЙ—КУЗНЕЦОВА

Y +1 s где а = -----=----;

2 ρ ₀ c ₀ ρ ₀ c ₀

параметр среды [8, с.

Y +1               -   - s =--- — нелинейный

2 22

27]; А 2 = — + — . В (6)

и далее штрихи у независимых пространственных переменных опускаются. Учитывая значение α , (6) перепишется в виде

В работе [6] уравнения (6) были уточнены для случая вязкой, теплопроводной жидкости. В нотации работы [13] уравнение для параксиального волнового пучка конечной амплитуды в вязкой, теплопроводящей среде имеет вид а д2р    д2р   c0     , b   д3р

--Р— + — А₂ р =--3—Р .

2 д т ²    д x д т   2          2 р ₀ c 0 д т ³

Y + 1     -Рр + C l а, р = о

4 р ₀ c ₀ д т ²    д x д т   2

(6а)

Здесь

К 4 Г 1 b = S + п + + к —

—

Если пучок обладает аксиальной симметрией, то (6) перепишется так (см., например, [5, (10)]):

а PL —^ р. + C o   + 1 *2 р = о, (₆б)

2 д т ²    д x д т   2 (д r ² r д r )

( ^c v    ^c p )

;

η и ς — сдвиго-

вая и объемная вязкости; κ — коэффициент теп-

лопроводности. Как видно, уравнение (7) получается из уравнений (6) добавкой неоднородного

где r = yy + z .

Наконец приведем уравнение (6б) в виде, представленном в [8, с. 227]:

члена, учитывающего вязкие и теплопроводящие свойства среды.

Отметим, что для нелинейных уравнений УХЗ (6) и УХЗК (7) характерна квадратичная нелинейность, а, например, при описании поведения оптических (электромагнитных) пучков возникает кубическая нелинейность (см., например, [2]).

—I ар-- д т (     д т

^{д р} У С о д x ) 2

( д ²  1 д V „

—2 +-- р ' = 0

₍ д r ²    r д r )

(6в)

ОБОБЩЕННЫЙ ВИД УХЗ

Как отмечено в [5], [13, гл. 9], [9, гл. 2, § 1], уравнение (6) учитывает одновременно и нелинейные искажения, и поперечные изменения возмущения, обусловленные дифракционной расходимостью. Поэтому можно утверждать, что уравнение Хохлова—Заболоцкой описывает во втором приближении распространение ограниченных пучков в нелинейных средах без потерь, т. е. является приближенным уравнением нелинейной акустики ограниченных пучков.

Отметим, что таким же по структуре уравнениям удовлетворяет возмущение давления p ' или колебательная скорость v _x . Это следует из справедливости линейной зависимости функций ρ ', p ', и v _x , верной с точностью до членов порядка ц : p' = c ₀ ² р и v x = c ⁰- р [9, с. 18, 19]. Отличие ρ ₀

заключается лишь в наличии корректирующего множителя у коэффициента α . В случае уравнения для p ' это будет коэффициент ₂ (см. далее c ₀ ²

В работах [14, 15] дана обобщенная форма записи УХЗ:

д (д p '     s    ,д p ' -z ,Р c₀

3— p   — L (p J 1 = — А 2 p дт ( дx c3р0 дт ) 2

Здесь p ' — акустическое давление (такое же уравнение записывается и для возмущения плотности р и для колебательной скорости); L (^) — линейный (в общем случае интегро-дифференциальный) оператор. Хронологически первым применил форму (8) В.П. Кузнецов [6]

L ( p ') =

b д ² p' 2 р о c о ³ д т²

Другие варианты использования оператора

L ( ^ ) приведены в работах [14, 15].

БЕЗРАЗМЕРНАЯ ФОРМА ЗАПИСИ УХЗ

В работах [15–17] УХЗ для пучков авторами этой формы записано в безразмерном виде d dV _ V dV 59 до 59

N (d 2 V 1 5 V )

+ .

4 (d ^ ² £ 5 ^)

Здесь V = p/ p₀ (или V = p'/p 0 ), где p ( p ' ) — возмущение плотности (акустического давления) среды относительно равновесного значения ρ ₀ ( p ₀ ); ρ ₀ ^' ( p ₀ ^' ) — исходная амплитуда поля ρ ' ( p ') или его пиковое значение, если исходный сигнал является импульсным; 9 = ют = = ю ( t - x / c 0 ) — безразмерное ("запаздывающее") время в движущейся системе координат, нормированное на обратную частоту (в этом случае ю = 2п f , f — частота) или длительность импульсного сигнала (в этом случае, очевидно, ю = 1/ A t , A t — длительность импульса); ^ = = r / a — нормированная поперечная координата, где a — радиус пучка; о = x / x SH — нормированная продольная координата, а x _SH — расстояние образования разрыва или нелинейная длина (см. [8, с. 34], [15, 16])

c ₀ ρ ₀ c ₀ ³ ρ ₀

^x SH =      । =       ।

εωρ ₀ εωp ₀

Число N (критерий Хохлова), являющееся единственным критерием подобия в уравнении (9) (характеризующее отношение нелинейной xSH и дифракционной xDIF

длин N = -x SH- ), равно [15- x DIF

N = ² c 4 P 0

22 '

εω ² a ² p ₀

Отсюда имеем для xDIF k2

x DIF = 2 a ,

^{2 c 0} ρ ⁰ .            (10)

22 '

εω ² a ² ρ ₀

ω k = —.

c ₀

Отметим, что существуют и другие модификации УХЗ, отраженные в обзоре [18] (см., например, выражения [18, (12)–(15)] и в [19–21]).

Замечание. Следует отметить некоторый разнобой авторов безразмерного УХЗ в записи уравнения (9) [15–17]. Так, в исходной работе [17] коэффициент при N в выражении (9) равен единице (там частично используются другие независимые переменные). В обзоре [15] этот коэффициент равен ½, а в работе [16] он, как и в выражении (9) у нас, равен ¼. При этом N определено во всех случаях выражением (10). В работе [21], опреде- ляющей алгоритм учета самовоздействия акустических пучков, этот коэффициент также равен ¼, однако в этой работе (по всей вероятности, вследствие описки) число N определяется выражением N _ 2c0 p0 _ 2c0 p0 , отличным от (10), при εω2a2p0 εω2a2ρ0

том что рассматривается то же УХЗ. Нами в Приложении были проведены самостоятельные выкладки по приведению уравнений (6)–(6в) для возмущения плотности ρ ' к безразмерному виду (9), в результате чего подтверждено, что коэффициент при N в (9) равен ¼.

О РЕШЕНИЯХ УХЗ

Отметим, что уже в момент публикации работы [5] было ясно, что общее решение уравнений (6)– (6в) в аналитическом виде представляет собой крайне сложную задачу. Насколько можно судить, до настоящего времени не найдено общего точного решения УХЗ. Поэтому заметные усилия ученых были направлены на получение точных частных решений, асимптотических и численных решений этой проблемы (см. монографию [19]). Были также исследованы некоторые свойства этого уравнения. Обо всем этом подробно изложено в обширном обзоре [15], посвященном 40-летию опубликования УХЗ в работе [5].

О САМОВОЗДЕЙСТВИИ (САМОЛОКАЛИЗАЦИИ) АКУСТИЧЕСКИХ ПУЧКОВ

Вначале отметим, что, в отличие от явления самофокусировки оптических (электромагнитных) пучков, в нелинейной акустике принято говорить о самовоздействии акустических пучков [20] по причине "занятости" термина "самофокусировка", обозначающего в акустике другие процессы. В акустике применяется также термин "самолока-лизация" [21]. Под этими терминами понимается волноводное (или самолокализованное по поперечным координатам) распространение волновых пучков различной природы.

В акустике это явление может быть вызвано различными причинами (см. обзор [15]), такими как тепловое самовоздействие акустических пучков, формирование потоков жидкости в поле мощной ультразвуковой волны, а также вследствие возможности взаимной компенсации дифракционной расходимости и нелинейной рефракции при неинерционном (нетепловом) проявлении нелинейности.

По-видимому, в работе [21] впервые теоретически показана возможность пространственного волноводного распространения акустических пуч- ков именно в условиях взаимной компенсации дифракционной расходимости и нелинейной рефракции, найдены точные решения, описывающие характерные профили волны в пучке, указана возможная схема практической реализации этого явления. Полученное решение являет собой пример асимптотически универсальных волн в неодномерном случае в том смысле, что, сформировавшись на каком-то расстоянии от источника, далее при распространении пучка волна не меняет своей характерной формы (стационарное решение). Ранее в одномерном случае такая асимптотическая универсальность была отмечена для пилообразной плоской волны [18]. Однако, в отличие от разрывной пилообразной волны, решение, найденное в [21], является гладким. Ниже приводятся основные результаты, полученные в работе [21].

За основу берется УХЗ в безразмерном виде (9). В стационарном по продольной координате σ д V „ случае, т. е. при — = 0, УХЗ (9) сводится к нели-до нейному стационарному по σ уравнению

YA У ) + 74 Y ( У ) = 0.

^N                         (13)

Y t( у ) + Y ( у ) Y 0 ( у ) = 0.

Найденное решение (12) уравнения (11а) представляет собой периодически повторяющиеся по θ симметричные куски параболы с изменяющимися вдоль координаты y крутизной ее ветвей и смещением параболы по вертикали относительно оси θ (см. [21, рис. 2]). Полученное решение является непрерывным и превращается в нуль в поперечном направлении за пределами пучка, включая его внешнюю боковую границу. Это же в [21] отмечается и для решений уравнения (11) в случае аксиально-симметричного пучка.

Наконец в [21] вычислены значения критерия Хохлова для уравнений (11) N ₃ и (11а) N ₂ (нижний индекс здесь отражает исходную пространственную размерность уравнений), которые равны соответственно

N (д 2 V 1 д V ) д а V ++ V

4 (д ^ ² ^ д ^ ) д О д О

N 3 » 0.35, N ₂ » 1.22.

или, будучи редуцированным для плоского случая ( x , У ) ,

N д 2 V д „ 8V + V—

4 д у ²   д о д о

(11а)

КРАЕВЫЕ И НАЧАЛЬНЫЕ УСЛОВИЯ ПРИ РЕШЕНИИ УХЗ

Для уравнений (6) типа ХЗ и (7) типа ХЗК обычно ставится такое краевое условие [15]:

р|₅ = F ( S ) Ф[ t + _V ( S ) ] .          (16)

Здесь p — давление на поверхности S , излучающей волну, на которой задаются начальная амплитуда F и фаза ψ колебаний, происходящих во времени по закону Ф( t). Как правило, исходный фронт полагается плоским или слабо искривленным, сферическим, для создания сфокусированного пучка. При этом краевое условие ставится на границе при x = 0 для кругового в поперечном сечении пучка и имеет соответственно вид p\x=0 = F ( r )Ф[ t ] ,

(17а)

(17б)

P l x = 0 = ^{F (} r ^)Ф

t +-- 2 c 0 R k

Здесь R _k — радиус кривизны исходного волнового фронта. В работах [9, 16, 17] и др. эти условия конкретизируются. Так, в работах [16, 17], в которых впервые было приведено УХЗ в безразмерном виде, краевое условие на плоскости x = 0 ставится так:

'    22            '    22

Р ' х = 0 = Р о e "     sin ®т = Р о e "     sin 0 =

= р₀e     sin tot

(17в)

Тогда исходная краевая задача (18), (19) преобразуется к краевой задаче (9), (20).

В [9] подробно рассмотрено также обобщение гауссова пучка при задании функции F ( r ) в виде

(напомним, что т = t --и при х = 0 справедливо c ₀

^Т х = 0 = t )•

В работе [9], посвященной получению численных решений УХЗ, приведенные краевые условия конкретизируются, а их разнообразие увеличивается. Далее при постановке начально-краевых условий будем оперировать с уравнением (6в), запи- ρ ' санным для поля p , учитывая, что p = —:

c ₀

F ( r ) = exp ( - r ” ) ,                  (21)

где n — безразмерный параметр. При больших значениях n (21) описывает платообразные распределения с довольно резким переходом в область тени.

В случае распространения сфокусированного пучка в нелинейной среде при рассмотрении уравнения (18) ставится следующее граничное условие [9, с. 52]

6 а  ,5 p   6 p )   c₀ 6 ²   1 6) ,

2 p— — I + — —2 +--I p ' = 0. (18)

6 т V c 2    6 т   6 х )   2 ^5 r ²   r 6 r )

^p '⁽ t , ^х , ^r )l х = 0

2 r = - F ( r ) sin to t +------

V    ² R k c 0

.

Заметим, что уравнение (18) отличается от (6в) 1

наличием у параметра α множителя ₂ . Уравне- c ₀

ние (18) в безразмерном виде также, как и уравнение (6в), преобразуется к уравнению (9) (см. Приложение), где величина V равна в случае уравне ния (18) (обозначения описаны выше) V = p'/ p0.

Начнем рассмотрение со следующего краевого условия [9, с. 30], эквивалентного (17а):

p '( t , ^r )l _х = ₀ =^- F ( ^r ) sin tot ,               ⁽¹⁹⁾

Здесь R _k — радиус кривизны волнового фронта;

F ( r ) = A exp

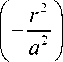
. Второе слагаемое под знаком

синуса в (22) учитывает в квазиоптическом приближении сферичность фазового фронта.

В случае рассмотрения безразмерного УХЗ (9) краевое условие (22) преобразуется к виду [9, с. 54]

V L = 0 =^- exp ^{(- 4 2})^sin

r

V

9 + ⁴ .

2в )

где F ( r ) — функция, зависящая от r , определяет амплитудное распределение на границе х = 0 (обычно в качестве F ( r ) принимается функция

F ( r ) = A exp

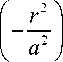
, и (19) в этом случае описыва-

ет гауссов пучок; A = const; а — эффективный радиус пучка). Тогда в (9) за величину V принимается значение V = p '/ A , где A — максималь

Здесь β — безразмерный параметр, характеризует геометрическую сходимость по отношению к дифракционной расходимости, равный, согласно [9, с. 54], отношению радиуса кривизны к дифрак-R ционной длине в = —г. ka2

Таким образом, в случае распространения сфокусированного пучка в нелинейной среде краевая задача имеет вид (18), (22) для размерного УХЗ и (9), (23) для безразмерного УХЗ.

ное значение функции F (r) (как правило, это осевое значение). И следовательно, в этом случае при трансформации от уравнения (18) к уравнению (9) во всех величинах p0 должно быть заменено на A , в том числе и в параметре N , который 2c4ρ в данном случае равен N = —    . Краевое усло-

εω2 a 2 A вие (19) с учетом (17в) преобразуется к виду

V L = 0 = - F ( « ) sin ⁰ ■    F ( 4 ) = F ( r ) •

^ = r / а .

О МОДЕЛЬНОЙ РЕАЛИЗАЦИИ ВОЛНОВОДНОГО РАСПРОСТРАНЕНИЯ (САМОЛОКАЛИЗАЦИИ) АКУСТИЧЕСКИХ ПУЧКОВ

Автору данного обзора неизвестны результаты проведения модельных расчетов по синтезу звукового поля для волноводного распространения (са-мовоздействия) звуковых пучков. Однако (далее цитата из [21]) "численные результаты, приведенные в [9, 18] (согласно нашей нумерации; прим. авт.), показывают, что когда для изначально сфокусированного звукового пучка эффекты нелиней-

ности и дифракции равнозначны (т. е. N ~ 1) и когда длина образования разрыва x _SH превышает фокальную длину (радиус кривизны исходного фронта), то тогда в фокальной зоне пучка формируется дугообразный волновой профиль … это значит, что при более тщательном подборе требуемых параметров область фокуса сама создает необходимые условия для дальнейшего волноводного распространения звукового пучка в условиях компенсации эффектов самовоздействия (дифракционной расходимости и нелинейной неинерционной рефракции)".

Из приведенных результатов очевидна "технология" модельного эксперимента. Приведем один из ее возможных вариантов применительно к аксиально-симметричным пучкам:

• 1)    рассматривается полупространство x >  0;

• 2)    в начало координат помещается фокусирующий аксиально-симметричный излучатель звукового сигнала конечной амплитуды;

• 3)    уравнение ХЗ в безразмерной форме (9) решается при варьировании критерия Хохлова N ₃ в окрестностях предсказанного в [21] значения (16), а также при вариациях радиуса кривизны излучателя;

• 4)    задача может считаться решенной, если при некоторых указанных параметрах (радиусе кривизны зеркала и критерии Хохлова N ₃ ) начиная с некоторого удаления от зеркала пучок приобретает стационарное волноводное состояние в продольном направлении.

ПРИЛОЖЕНИЕ

Приведение УХЗ (6в) и (18) к безразмерному виду

Ниже приведены цепочки преобразований уравнений (6в) и (18) к безразмерному виду.

Уравнение (6в):

д Г   д р   д р )   с₀ д ²   1 д )

• 1)    —I ар— ---— 1 + — —2 +--I р = 0, д т к     д т    д x )  2 кд r ²   r д r )

  
  

  (

  _'

  
  

  Т" ^аР о V д т

  
  

  ''

  ^д Р о V ^д P o ^V ---

  
  
  
  
  
  

  к

  
  

  д т      д x

  )

  
  

  д Г ( ' V тА V I ^а ( Р о ) V _z д т к \ /     д т

  
  

  —

  
  

  + c o

  
  

  Гд 2    1 д)

  —2" +---I Р _о V = 0, 2 к д r ²    r д r )

  
  

  ' д V ) с₀ ' Р о^ I ⁺ Т Р о д x ) 2

  
  
  
  

  к

  
  

  -^2-+ 1 A] v = о, д r   r д r )

  
  

  θ

  т = —, ω

  
  

  6) d т = -d y , ω

  
  
  
  

  д     д

  ---= 6 9 , д т     д О

  
  

  д Г / ' V т/д V    ' д V ) с₀ '

  8) ^-1 ^а® ( Р о ) V — ^— Р о— I + — Р о д О к    \   ’   дО       д x ) 2

  
  

  дР кд r²

  
  

  +¹ — I V = 0, r д r )

  
  

  9) ^x = x sh X ,

  
  

  10) F = д x

  
  

  1 д

  x sh д X ’

  
  

  с

  
  

  д^Г

  11) ®— а® д е

  
  

  ( Р о )

  
  

  к

  
  

  ।² V * д е

  
  

  —

  
  

  р 0 д V ' x sh д X ^

  
  

  + c ⁰

  
  

  Р 0

  
  

  к

  
  

  4+ ¹ -1 V _ 0, д r    r д r J

  
  

  12) r = aR ,

  
  
  
  

  _д_ £ д д r  а д R ’

  
  
  
  

  д ω д е

  
  

  Г ^а^⁽Р 0 )

  к

  
  
  
  

  v *

  д е

  
  

  _—

  
  

  р 0 д V ' ^ sh д X _v

  
  

  '

  
  

  д ²    1 д

  
  
  
  

  а

  
  

  с

  
  

  '

  
  

  д е

  
  

  к

  
  

  / ,\²_лд V ®р д V а® _о V ---⁰ —

  ρ ₀

  
  

  x sh д X ^

  
  
  
  
  
  

  ^д 2 V* αω ² ρV

  д е ⁰

  
  

  _'

  
  

  д V

  
  

  —

  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  

  к

  
  

  д е

  
  

  + c ⁰ Р    ■

  
  

  кд R

  
  
  
  

  r a r

  
  

  V = 0,

  
  

  '

  
  

  c ₀ ρ ₀

  
  

  д ²    1 д

  
  

  +—— — ।

  
  

  2 a

  
  
  
  

  кд R

  
  
  
  

  R д R

  
  

  V _ о,

  
  

  ε а =---- ,

  ρ ₀ c ₀

  
  
  
  

  ^д        2  ' _Тл^д V

  εω ² ρV д е       ⁰

  
  

  _'

  
  

  д V

  
  

  _—

  
  

  к

  
  

  д е

  
  

  c ₀ ρ ₀

  x sh =        ' ,

  εωρ ₀

  
  

  С

  
  

  д ₂ V.u, — s® pV— де ⁰ де

  
  

  к

  
  

  _'

  
  

  Г д ²    1 д

  
  

  ® ^ V 1 + c 0 - -^ + x _sh д X J  2 а ² "

  
  
  
  

  кд R

  
  
  
  

  R д R

  
  

  V = 0,

  
  

  Р 0 ^c 0 ® ^{д V} |+ ^p 0 c 2

  
  

  x sh   ^{д X}

  
  
  
  

  1 a ²

  
  
  
  

  к

  
  

  д ²

  дR^{2 +}

  
  

  1 д

  
  

  R д R

  
  

  V = 0,

  
  

  _'

  
  

  д V S®p₀р₀c₀® д V

  
  

  д е

  
  

  _—

  
  

  к

  
  

  С 0 Р 0    д X ^

  
  

  +

  
  

  ρ ₀ c ₀ 1

  
  

  2 a ²

  
  

  г

  
  

  к

  
  

  д ²

  дR^{2 +}

  
  

  1 д

  
  

  R д R

  
  

  V _ 0,

  
  

  д Г ₂ -_лд V ₂ ‘ д V -- S® pV--Eto р-- д е к       д е       д х

  
  

  _'

  
  

  ‘ д V

  
  

  д X

  
  

  +

  
  

  ρ 0 c 0 1

  
  

  2 a ²

  
  

  г

  
  

  д ²

  
  

  1 д

  
  

  +

  кд R ² R д R

  
  

  V = 0,

  
  

  д Г а V д V 1 — V ---+

  д е к д е д х J

  
  

  N _ ^{2 С} 2 ^р 0 ,

  22 ' εω ² a ² ρ ₀

  
  

  У V *

  
  

  д V

  
  

  _—

  
  

  д е к д е   д х

  
  

  Уравнение (18):

  
  

  _п д г    ,д р' д р

  1) I ар

  д т к д т    д x

  
  

  c ₀ ² ρ ₀

  
  

  Г д ²     1

  
  

  2 s® ² а ² р ₀ к^{д R}

  
  

  д

  
  

  R д R

  
  

  V _ 0,

  
  

  N Г д ²   1 д

  +— —+--- V _ 0.

  4 кд R ² R д R J

  
  

  + c ⁰

  
  

  Г д ²    1 д

  —2 +---I Р _ 0, 2 к д r ²    r д r J

  
  

• 2)    Р = ^

c ₀

д а ,5 p д p ) c₀ д ²   1 d )

• 3) . p          1 +    —2 + \ p = 0

д т ( c 0 д т д x J 2 (д r ² r д r J

• 4)    P ' = P o V ,

  
  
  
  

  д а _v — — p 0^V д т c,

  
  

  α

  
  

  '

  ^д p 0 ^{V   5} P 0 ^V

  ---- — ----

  
  
  
  

  V

  
  
  
  

  д т

  
  

  д x

  J

  
  

  + c ⁰ 2

  
  
  
  

  V

  
  

  д 2 1 д ] _n —2 +— \ p ₀V = 0, д r ² r д r J

  
  

  д ( а V V    д V )

  2 p ₀ V--p ₀— I

  д т V c 2      д т       д x J

  
  

  c

  
  

  г

  
  

  д

  
  
  
  

  1 д

  
  

  V c ₀

  
  

  + -°- p₀ ^ + - — V = 0, 2 0     2

  
  

  V

  
  

  д r

  
  

  r д r

  
  
  
  

θ т = —, ω

d т = — d е , ω

д     д

— = to —, д т     д е

д( а   о_{т л}д V д V )   c (д ²   1 д)

• 10)    to--top₀V--p₀— + — p₀ —₇ +-- V = 0,

  V c ₀

  
  

д е V c 0 д е    ⁰ д x J   2  ⁰ (д r ²    r д r J

• 11)    x = x sh X ,

• 12)    — = ——, д x x _sh д X

  д а    2_{T л}д V

  13) ω      ω p ² V

  д е c 0    ⁰ д е

  
  

  —

  
  

  V c ₀

  
  

  p 0 ^{д V} L £ 0 _n

  ^{+ p} n

  x _sh д X J  2 ⁰⁰

  
  

  г

  
  

  V

  
  

  -^д-_г+- — I V = 0, д r   r д r J

  
  

• 14)    r = aR ,

• 15)    F = ¹   ,

д r a дR д (а    2тлдV

16) ^to^ “^to p VIP д е c ₀        д е

—

( д ²    1 д

V c 0

p 0 ^{д V} 1 + c 0 p 0   -    .

x _sh д X J   2 a²

(д R

R д R

V = 0,

^- f^to2 p2V   — top0 5V де c2     0 де

f д ²    1 д

—

V

+ c 0 £0 _ + x sh д X J  2 a ²

(д R

R д R

V = 0,

д а _{2 v} dV ω ² p V 20

( д ²    1 д

—

V c ₀

to ^ 1+ c 0 ± _^+ x _sh д X J  2 a a

(д R

R д R

V = 0,

αε

=    3, c2   ρ0c03

20) —^f Eto ² pV — - ^c³^ — 1 + ^cc ⁰- 4 f^T +   ^ V = 0

X, = sh

c ₀ ³ ρ ₀ εωp ₀

d (  2 _v VV

εω ² p V

₂ d V 1

- Sto p_n— +

⁰ d X J

ρ ₀ c ₀⁴ 2 a ²

fd ²

dR2 ⁺

(d R

I d 1

V = 0,

24) —^f V ^V-^^ )+ ^P 0 ^C 0      + -—¹ V = 0

d e ( d e d X J 2sto ² a ² p ₀ (d R ² R d R J

N = ^{2 c 4 p} 0

εω ² a ² p ₀

26) — d e

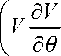
d V I N ( d²

--- +--T dX )  4 (dR2

V = 0.

О точности задания параметров при решении УХЗ

Указанный вопрос требует специального исследования. При оценке значимости точности параметров задачи следует исходить из того, что основное уравнение УХЗ получено с точностью O ( p ² ) , поэтому нет нужды задавать параметры задачи с точностью больше той, которая приведет к превышению базовой точности (см., например, рассуждения на эту тему в работе [6]). Вначале поэтому опишем технику оценки μ .

Оценка величины μ

Согласно изложенному выше, суперпозиция плоских волн с близкими по направлениям волновыми векторами может дать локализованное в поперечном направлении поле — волновой пучок с почти плоским волновым фронтом. Поэтому правомерно использование отношений возмущений полей давления p 'и плотности ρ ' к их равновесным значениям p ₀ , ρ ₀ , а также колебательной скорости u и равновесной скорости звука c 0 , характерных для поля плоской звуковой волны [11, с. 20]; это отношение в нелинейной акустике обозначают через μ :

u- = P l= 4- .           (П1)

c ₀ ρ ₀ c ₀ ² ρ ₀

Приведем также выражения для объемной плотности энергии и интенсивности (силы) звука в гармонической плоской звуковой волне [22, с. 14]. Объемная плотность энергии E в плоской волне равна

E = p4 = Po u2.(П2)

ρ 0 c 0 ²

Интенсивность (сила) звука J в такой волне равна [22, с. 14]

J = p u = c0E = p0c0u =----.(П3)

ρ ₀ c ₀

С помощью выражений (П1)–(П3) можно связать величины μ , E и J . Например, из (П3) имеем

E = Po u2 = Po c 2 p2,(П4)

J = poc0u = poc0 p .

В случае гармонического сигнала в выражениях (П4) и (П5) вместо величины u ² должна появиться эффективная величина u ₀² /2, где u 0 — амплитуда поля u . Тогда выражения (П4), (П5) преобразуются к виду

E = p ₀ u °L = ^{P 0 C} L p 2,              (П4а)

u 0    ρ 0 c 0  2

J = ^р о c о 2 = 2 ^ц .

(П5а)

Здесь E и J — соответствующие осредненные за период значения величин E и J .

Таким образом, зная параметры поля в квази-плоском пучке, мож н о по объемной плотности звуковой энергии E ( E ) или силе звука J ( J ) оценить параметр μ .

Отметим, что реальные возмущения малы по сравнению с равновесными значениями. В качестве ориентира сошлемся на пример из [9, с. 17]: при излучаемой интенсивности звука J = 0.3 Вт/см² возмущение плотности или колебательная скорость в воде таковы, что ^р ~ 10 - 5 , М ~ 10 - 5 .

ρ ₀

c ₀

Каноническое уравнение ХЗ первоначально было опубликовано в виде (6) для избыточной (возмущенной) плотности ρ ' . На практике вместо уравнения (6) может оказаться удобнее рассматривать УХЗ в терминах избыточного давления p ' (18). Наконец оба приведенных выше размерных УХЗ могут быть представлены в единой безразмерной форме (9) с критерием Хохлова, определяемым выражением (10) в терминах амплиту-

'

'

ды p ₀ избыточного давления либо амплитуды ρ ₀ избыточной плотности.

В уравнениях (6) и (18) присутствуют два постоянных параметра: α и c ₀ . Как отмечалось выше, уравнения (6) и (8) содержат члены, не превышающие порядок O ( ц ² ) . Поэтому при оценке точности, с которой должны задаваться параметры α и c ₀ , целесообразно пренебрегать избыточной точностью их оценки. Пусть, например, параметр α исходно известен с точностью α ₀ . Если его оценить с точностью O ( 5 ) по отношению к а₀

а = а₀ + 5а 1 ,

Второй возможный подход оценки необходимой точности параметров, фигурирующих в УХЗ, является не столь очевидным и отталкивается от представления УХЗ в безразмерном виде (9), (10). Кроме того, ниже при описании этого подхода учитывается тот факт, что самовоздействие звуковых пучков, описываемых УХЗ, возможно в малой окрестности некоторого значения критерия N (см. выше).

Рассмотрим УХЗ в безразмерном виде (9), (10). Как видно из (9), его решение определяется только значением параметра N (10). Реально величины из этих уравнений ρ 0 , ω , a , p 0 ^' и ρ 0 ^' можно считать известными. Нелинейный параметр среды

Y + 1

е = и невозмущенная скорость звука c0 мо гут зависеть от учета ряда факторов, таких как температура, коэффициент всестороннего сжатия, вязкость, соленость и т. д. Зависимость от термодинамического параметра T (температуры) здесь не рассматривается, т. к. это приведет к необходимости решения связанной системы уравнений, в которой помимо УХЗ должно будет фигурировать уравнение сохранения энергии либо уравнение теплопроводности, т. к. от поля T зависят и давление, и плотность жидкости.

Предлагается следующий механизм оценки границ точности параметров ε и c ₀ при решении уравнения ХЗ в безразмерном виде (9), (10). Пусть в результате его решения получена некая кривая S = S ( N ) зависимости эффекта самовоздействия от критерия подобия N . Согласно [21], эта кривая имеет единственный экстремум при N = N ₀, когда эффект самовоздействия максимален S ₀ = = S ( N ₀ ) = max. При всех остальных известных величинах в (10) при N = N ₀ будет определено

и отношение

Г c 4 )

0 для поля избыточного давле-

I е ) о

где величины α ₀ , α ₁ — величины одного порядка, то в уравнениях (6) и (18) появятся дополнительные члены. Те из них, которые превысят порядок O ( ц ² ) , должны быть отброшены так же, как были отброшены соответствующие члены при изначальном выводе этих уравнений. В этом состоит первый очевидный подход при оценке необходимой точности задания параметров уравнений (6) и (18). Для его реализации необходимо только оценивать параметр µ с помощью техники, описанной выше.

ния или

0 для поля избыточной плотности.

I е ) о

Если выделить окрестность точки N ₀ такую, что для точек N 1 <  N ₀ и N ₂ >  N ₀ кривая впервые достигла какого-либо еще приемлемого значения (например S 1 = S ₂ = 0.7 • S ( N ₀ ) , где S 1 = S ( N 1 ) , S ₂ = S ( N ₂ ) ), то очевидно, что нет смысла улуч-

шать точность отношений

( с„ ⁴ ^

0 или

I е к

Г е„ ² ^

-°- I , при ^-

I ^е ) о

ближая их к реальным, если результирующее

значение N вышло за границы интервала N ^ [ N i , N 2 ] .

Таким образом, в рамках этого раздела Приложения предложены два подхода для обоснования априорной точности расчетов некоторых параметров при решении задач, связанных с УХЗ.