О восстановлении аналитической функции в спиральной звезде Миттаг-Леффлера по значениям на множестве единственности
Автор: Яковлев Е.И.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 1 т.17, 2016 года.
Бесплатный доступ
В случае одного комплексного переменного традиционным множеством единственности в классе аналитических функций является множество, содержащее предельную точку. Наиболее известным множеством единственности в многомерном случае является «вещественная» окрестность точки. Для определенного класса областей множество единственности в многомерном случае может быть уменьшено. Например, в работах С. В. Знаменского указывается счетное подмножество на остове полидиска, по значению на котором голоморфная функция восстанавливается во всем полидиске. Иногда функция может быть продолжена и в большую область. Так, в работах Ж. Адамара, Г. Миттаг-Леффлера, Ле Руа, Линделефа были предложены методы суммирования, дающие хорошие результаты для аналитического продолжения степенного ряда в случае звездных областей комплексной плоскости. В дальнейшем, для одномерного случая в работах Н. У. Аракеляна был предложен метод восстановления аналитического элемента с помощью универсальных матричных методов суммирования в классе спиральных областей. Настоящая работа посвящена восстановлению аналитической функции, заданной на счетном множестве единственности остова полидиска, в максимальную спиральную область, называемую (m,α)-звездой Миттаг-Леффлера данной функции. Восстановление производится с использованием многомерных матричных методов суммирования кратного степенного ряда, которые строятся с помощью одномерных матричных методов суммирования степенного ряда. При этом апробация построенных многомерных матричных методов суммирования кратного степенного ряда проводится с помощью одномерной геометрической прогрессии.
Кратный степенной ряд, множество единственности, звезда миттаг-леффлера, главная звезда, аналитическое продолжение, суммирование кратного степенного ряда, матричные методы суммирования, спиральные области, области эффективной суммируемости
Короткий адрес: https://sciup.org/148177527
IDR: 148177527 | УДК: 517.55
Текст научной статьи О восстановлении аналитической функции в спиральной звезде Миттаг-Леффлера по значениям на множестве единственности
Введение. Примерно сотню лет назад ученые начали использовать теорию функций комплексных переменных для описания неравномерных полей, для моделирования сложных потоков, для описания вращающихся полей и стали получать модели комплексных переменных, которые значительно проще описывают сложные объекты и явления, нежели модели действительных переменных. Задачи гидродинамики и газовой динамики, авиастроение, самолетостроение и ракетостроение используют комплексные переменные как основной математический инструмент моделирования. Например, теория подъемной силы крыла самолета опирается на построение аналитической функции, которая носит имя «дедушки» русской авиации Жуковского. Теорема единственности определяет одно из классических свойств аналитических функций. Если из обращения аналитической функции на множестве следует ее тождественное равенство нулю, то обычно такое множество называют множеством единственности.
В случае n -мерного комплексного пространства С * множеством единственности является «вещественная» окрестность точки. В зависимости от вида области размерность множества единственности может быть уменьшена. Обычно это наблюдается для тех областей в С , у которых граница Шилова области является собственной частью границы самой области. Особенно наглядно это получается в случае полицилиндра. Классическая формула Коши восстанавливает значение функции, голоморфной в полидиске, по ее значениям на остове полидиска. В работах [1; 2] С. В. Знаменского указывается счетное подмножество на остове полидиска, по значению на котором голоморфная функция восстанавливается во всем полидиске.
В некоторых случаях функция может быть продолжена в большую область. Вопросам аналитического продолжения степенного ряда, в частности путем переразложения ряда, в случае одного переменного посвящена монография [3], содержащая соответствующую библиографию. В дальнейшем, более эффективные методы суммирования степенного ряда (аналитического продолжения с помощью матричных методов) были предложены Миттаг-Леффлером, Лин-делефом, Ле Руа и другими математиками (см., например, [3-5]). Для n = 1 в случае звездных областей достаточно подробная библиография имеется в [6-8], для случая спиральных областей - в [9]. В дальнейшем, Аракеляну [9] удалось показать, что аналитическое продолжение однократного степенного ряда с помощью матричных методов суммирования возможно только в спиральные области.
В случае многих переменных в работах [10-13] предлагаются различные методы суммирования кратного степенного ряда для звездных областей. В [14] предложен метод, позволяющий суммировать крат ный степенной ряд в случае параболически звездных областей (см. ниже определение 1, при а = (0, .„, 0)). В работе [15] предлагаются методы суммирования кратного степенного ряда, позволяющие суммировать этот ряд в классе областей в С, естественным образом обобщающих как спиральные, так и звездные.
Используя формулу из [1; 2], восстанавливающую аналитическую функцию в единичном полидиске по счетному множеству единственности на остове полидиска, в настоящей работе по значениям функции на дискретном множестве единственности, расположенном на остове полидиска, функция восстанавливается в произвольной спиральной звезде Миттаг-Леффлера по схеме, предложенной в [15].
Основные обозначения и формулировки. Обозначим z = (zi, .., zn) - точки n-мерного комплексного пространства С,
R n : = { x е R n ; x > 0, ..., x n > 0 } ,
Г r = | z е Cn : | Z j | = r j } ; k = ( k 1 , ..., k n ) - мультииндексы, II k || = k 1 + ... + kn , k ! = k 1 !... k n ! , Zk = Z 1 k 1 . .... ^,
U r = U n ( Г 1 , ..., r n ) = { z е C n :| z j < r j } , U = U n (1, ...,1), {m , J — : m . n е N .
n J
Пусть
II МИ n-кратный степенной ряд, который сходится в некотором полидиске Ur в С. Функции, голоморфные в Ur и непрерывные вплоть до замыкания Ur , обозначим A (Ur). Для таких функций классическая формула Коши позволяет восстанавливать их значения внутри полидиска по значениям функции на остове.
В [1; 2] решается задача восстановления функции из A(U) по значениям этой функции на дискретном множестве единственности, расположенном на остове единичного полидиска U. Пусть положительные числа Ь1, ...,bn выбраны так, что величины ln b 1, .
..., Inbn вместе с числом л линейно независимы над кольцом целых чисел, тогда набор точек р = {bi-)” = {b/v, ...,b"}”
v=-ro v= является множест-
вом единственности для функции, голоморфной в единичном полидиске U и непрерывной вплоть до его остова. Формула, восстанавливающая функцию f по набору Р, анонсирована С. В. Знаменским в [1], ее подробное доказательство изложено в [2]. Приведем полную формулировку теоремы из [2].
Теорема А ([2], с. 47, теорема 1). Пусть f е A(U ).
Тогда при z е U
f(zi, ■■■,zn) = j. 1 m f (bik) (2)
mm" 2m kE„ (1 - Zib^k^„(i - znb^k)), где последовательность 5(k) определяется выбором p.
При 5 ( k ) = - ik формула верна для всех z е U ■
Замечание 1 ■ Формула (2) восстанавливает функцию f ( z ) в замыкании единичного полидиска по дискретному множеству р, последовательность 5 ( k ) определяется выбором p. Для внутренних точек полидиска можно взять 5 ( k ) = - ik ■ Поэтому в дальнейшем будем считать 5 ( k ) = - ik ■
Замечание 2 . Формулу (2) с помощью замены несложно выписать для произвольного полидиска U r = U" ( r i , ..., r n ) с радиусами ( r i , -„, r n ):
f ( - 1 , --- , Z n ) =
11m ' m f 1 rb 1_____________ m — 2 m k~„ (1 - Z i r b i 5 ( k ))-(1 - z n r n - 1 b n 1 k ) )
Задача аналитического продолжения функции, заданной кратным степенным рядом, в спиральную область с помощью одномерных матричных методов решена в [15], Для формулировки основного результата настоящей работы приведем определение класса областей из [15]-
Определение 1 ■ Пусть x е R” , а е Rn ■ Множество G в С” назовем (х, а)-спиральным относительно начала координат, если вместе с каждой точкой 0 0 -,0\ z = (Zi, ■■■,zn) в множестве G содержится (х, а)-отрезок
L x , а ) : = { z е Cn : z, = z 0 1 ’ i а 1 ), -„ z 0 1 i ’
■ ■■, z n = z 0 t x n (1 + i а n ) , t е [0,1]} c G ■
Если функция fz ) голоморфна в некоторой окрестности начала координат в С ” , то максимальную ( х , а)-спиральную область G f , а , в которую голоморфно можно продолжить функцию f назовем ( х , а)-спиральной звездой Миттаг-Леффлера функции f или просто ( х , а)-звездой. Максимальная звездная область G , в которую голоморфно продолжается ряд (1), называется звездой Миттаг-Леффлера (или главной звездой) ряда (1) или функции fz )■
Понятие ( х , а)-спиральной звезды Миттаг-Леффлера шире понятия звезды Миттаг-Леффлера. Соответствующие примеры имеются в [13-15]. Для n = 1 класс ( х , а)-спиральных областей переходит в спиральные области (см. [3], с 40 и [9], с 38)■
Цель настоящей работы, опираясь на представление функции в единичном полидиске из [2], формулу (2) и результаты из [15], - доказать формулу, позволяющую восстановить функцию f в ее ( x 1, ■■■, xn ; а , ■■■, а ) -звезде Миттаг-Леффлера по значениям этой функции на дискретном множестве единственности, расположенном на остове единичного полидиска U ■ Основным результатом работы является следующая теорема.
Теорема 1. Пусть f е A(U), x е Q" ■ Тогда для z е Gfx,а) справедлива формула f (z1, ■■■, zn ) = m (3)
= 11m 11m— £ f ( b - k T x ; a , p ) ( z i b , -, b ), ' '
P^P0 m^^ 2mk =-m где метод суммирования T(x;а) построен по одномерному методу Та из класса 5 по формуле (6).
Следствие 1. Формула для произвольного полидиска с радиусами r = ( r1, ■■■, rn ) имеет вид
f(z1, ■■■, zn ) = mГ
= 11m 11m--- У f ( rb,k )Taol -1 bk
(x ;a,P)i
P^P0 m^» 2m k=-m^
■ ■ ■
z n ik n
n
■
Замечание 3 . Если бы можно было переставить местами пределы (а это заведомо можно сделать внутри полидиска) и перейти к пределу по р, то мы получили бы формулу (2) для полидиска из теоремы Л^
Приведем необходимые для доказательства теоремы 1 формулировки и понятия из [15]^
Пусть P = {p} - множество на вещественной оси, имеющее предельную точку р0 такую, что p 0 г P , и пусть
T T ( z ) = S c k ( P ) z k = E c k i- kn ( P ) z\- zk n " (4)
|| k || > 0 || k || > 0
степенной ряд, коэффициенты которого зависят от произвольного P е P , сходящийся в С ” ■
Определение 2 ■ Будем говорить, что матрица T = { c k ( P ) } = { c k^kn ( P ) } или матричный метод Т суммирует ряд (1) в области О ( f е H ( Q )), если:
-
1) композиция Адамара рядов (1) и (4)
при фиксированном p е P абсолютно сходится в некоторой полной, логарифмически выпуклой, области, содержащей Q ;
-
2) локально равномерно в Q (равномерно на любом компакте из Q) выполняется равенство
f ( z ) = 11m T , * f ( z ), V z еQ .
P^P 0
Замечание 4 . Можно рассматривать класс матричных методов Т , которые при p е P не задают целую функцию, но выполняется условие 1. Это существенно расширит класс рассматриваемых методов, но вызовет определенные трудности при проверке условия 1- Если ряд (1) сходится в непустой окрестности 0 и матричный метод Т при p е P задает целую функцию, тогда условие 1 не требует проверки, оно выполняется автоматически■ Что и предполагается в настоящей работе.
Для одномерного случая теорема Окада [6; 9] позволяет апробировать каждый из матричных методов лишь на геометрической прогрессии Если матричный метод суммирует геометрическую прогрессию в ее а-спиральной звезде Миттаг-Леффлера, то этот метод суммирует любую функцию в ее а-спиральной звезде Миттаг-Леффлера. Для многомерного случая вариант теоремы Окада для случая звездных областей предложен в [13].
Опишем класс одномерных методов суммирования, необходимых для построения многомерных методов, используемых в теореме 1.
Определение 3 . Обозначим через 5 класс одномерных методов суммирования (полунепрерывных матричных методов) Т а = ^ Т ( р ), ре P } со свойствами:
ГО
-
1. Функция Ф т ( X ) = I Т^ ( р ) Х k является целой k = 0
-
2. Матричный метод Т а суммирует геометрическую прогрессию g ( X ) = (1 - X ) 1 всюду в ее а-спиральной звезде Миттаг-Леффлера G “ x^i . То есть локально равномерно выполняется равенство
для произвольного ре P , Хе C .
(1 -X ) - 1 = lim Д *(1 -X ) - 1, VX е G ;
т^т о (1 Х )
Произвольному матричному методу из класса 5 и V x е Q „ можно поставить в соответствие многомерный матричный метод по правилу
Т ( x ; a ) : = { T <“ k , „ > ( р ), ре P } , (6)
где m = ( m 1 , ..., m „ ) - первая целочисленная точка с положительными координатами, лежащая на луче, выходящем из нуля и проходящем через точку х . Для дальнейшего изложения нам необходима теорема об аналитическом продолжении с помощью матричных методов. Приведем ее полную формулировку из [15] в удобном для дальнейшего использования виде.
Теорема B. Пусть функция f задана кратным степенным рядом (1), сходящимся в окрестности нуля в С”, x е Q„, Gfx,а) - ее (x1, ...,xn; а, ...,а) -спиральная звезда Миттаг-Леффлера и многомерный метод Т(x;а) построен по одномерному методу Та из класса 5 по формуле (6). Тогда всюду в G(x,а) метод Т(x;а) локально равномерно суммирует функцию f. То есть справедлива формула f (z) = lim FX;„)(z), Vz е G.,а), (7)
р^ро где F(x ;а)( z) = I Т<“ , m > (р) ak1... knZ1 -z„k" , Те P -||k||>0
композиция Адамара ряда (1) и ряда
^ ; а ) ( z ) = I Т а , m > ( р ) z z^ n , ре P .
II k || > 0
С помощью теоремы удобно конструировать многомерные матричные методы по одномерным. К сожалению, суммировать такие методы могут кратные степенные ряды в спиральных звездах только с когерентной мнимой частью, т. е. при а 1 = ... = а „ = а .
Основные доказательства. Теорема В позволяет восстанавливать функцию по ее значениям на достаточно «тонких» и даже дискретных множествах во всей спиральной звезде Миттаг-Леффлера. Для доказательства теоремы 1 нам потребуется лемма.
Лемма . Пусть x е Q > , f е A (U r ), G ( x , а ) - ее
( x 1 , ..., x n ; а , ..., а )-спиральная звезда Миттаг-Леффлера и многомерный метод Тx ; а ) построен по одномер
ному методу Т а из класса 5 по формуле (6). Тогда всюду в G (x , а ) справедлива формула
f ( z 1 , ..., z „ ) =
lim------ р^Ро (2лi)„
J f (О Т ( x ; а , р ) Г r
z | d 2?J 2 ’
z е G f x , а ).
G ( x , а )
( x 1 , ..., x n ; а 1 , ..., а „ )- звезде f. Здесь а 1 = ... = а n = а .
Замечание 4 . Лемма показывает, что функцию можно восстановить в спиральной звезде по значениям на остове полидиска. Если бы можно было переставить местами предел и интеграл, то мы получили бы интегральное представление Коши для полидиска.
Доказательство леммы . Для внутренности полидиска Ur формула доказывается простым разложением в ряды подынтегральных функций с последующим их перемножением и почленным интегрированием. Для точек, принадлежащих ( x 1 , ..., x „ ; а , ..., а )-звезде f, следует воспользоваться теоремой В из статьи [15] о суммировании матричными методами в спирально-когерентной области.
Рассмотрим интеграл в правой части формулы (8) и разложим подынтегральное выражение в степенные ряды:
-1— J f ( ^ ) Т ( x ; а , р ) f £ |~ = „ , р
(2лi) Гr k2j 2
(2 Л i ) Ur I| k || > 0
k 1
G . I C kx... k n (р) UI || k || > 0 12 1 J
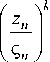
dc 2
В подынтегральном выражении первый ряд сходится абсолютно, а второй представляет целую функцию, поэтому их почленное произведение представляет степенной ряд, сходящийся равномерно и абсолютно по переменным 2 на остове полидиска при
произвольном z е C „ . Следовательно, ряд, полученный произведением указанных рядов, можно почленно проинтегрировать по остову полидиска. Воспользуемся известной формулой
(2 K i ) „ J2 „k '"' 2 ""d 2 Г r
1,( k 1 , ..., k „ ) = ( - 1,..., - 1),
0, ( k 1 , ..., k „ ) ^ ( - 1, ..., - 1). ( )
Интегрируя, получим правую часть формулы (7):
Т * f ( z ) = V е, ( р ) a,zk = V c, , ( р ) a, k z k1 ... zk „ .
р k k k | ... k „ k | ... k „ 1 n
|| k || > 0 || k || > 0
В силу формулы (7) теоремы В
f ( z ) = lim T p * f ( z ), V z e G fx , a ).
P^Po
Лемма доказана.
Доказательство теоремы 1 . Следуя лемме, представим функцию fz ) по формуле (8), здесь полидиск Г r компактно лежит внутри единичного полидиска. Поэтому подынтегральную функцию можно заменить по формуле (2) из теоремы А:
f (, ..., z ) = lim —1—
1 p'p (2 ^ i ) n
1 ^
x [ lim — У 2 X -
1 r
f ( b i )
(1 -c b iv )...(1 -c X )
z | d c cj c
-T, ( x ; « , p )
Так как сумма при каждом v конечна, подынтегральное выражение непрерывно зависит от v, интеграл сходится равномерно и абсолютно, а также переменные интегрирования не зависят от предельного перехода при произвольном z из некоторого компакта, то можно знак предела и суммы вынести за знак интеграла:
1 m 1
f ( z 1 , ..., z n ) = lim lim— E f ( b )~44 x p^p o m ^™ 2 m v =- m (2 л i )
r_________1_________T (z) d?
Гг (1 -C 1 b i )...(1 -C b ) ( x ; “ , p ) (cj c .
В подынтегральном выражении первый сомножитель можно разложить по степеням ?, и полученный степенной ряд будет сходиться абсолютно и равномерно на остове полидиска Гr. Второй сомножитель представляет целую функцию по переменным ? на остове этого полидиска при произвольном z e C ” . Почленное произведение этих двух рядов представляет степенной ряд, сходящийся равномерно и абсолютно по переменным ? на остове полидиска при произвольном z e C ” . Однако следует заметить, что подынтегральное выражение будет равномерно ограничено лишь при z e Gfx,a). Следовательно, ряд, полученный произведением указанных рядов, можно почленно проинтегрировать по остову полидиска. Воспользуемся формулой (9). После интегрирования для z e Ur правая часть, очевидно, будет стремиться к f (z) . В силу теоремы В, для всех z e G(x,a) правая часть будет равномерно ограничена при произвольных р и X. Опираясь на теорему Монтеля (принцип компактности аналитических функций), получим f (z1, ..., zn ) =
^
= lim lim — E f ( b v ) T ( x ; a , p ) ( z 1 b iv , ..., b );
p^p o ^” 2 X v ~^
z e G (’a\
Теорема 1 доказана.
Заключение. С помощью формулы (3) из теоремы 1 можно восстанавливать голоморфную функцию внут ри спиральной звезды Миттаг-Леффлера, зная ее значения на счетном множестве единственности, расположенном на остове единичного полидиска. Следствие 1 позволяет перейти к полидиску с произвольными радиусами.
Список литературы О восстановлении аналитической функции в спиральной звезде Миттаг-Леффлера по значениям на множестве единственности
- Знаменский С. В. Связь аналитических функций многих переменных с рядами Дирихле одного переменного. Приложение к представлению нелинейных аналитических операторов//Докл. АН СССР. 1975. Т. 223, № 3. С. 544-547.
- Знаменский С. В. Связь аналитических функций многих переменных, аналитических функционалов и операторов с рядами Дирихле одного переменного и некоторые ее приложения//О голоморфных функциях многих комплексных переменных/ИФ СО АН СССР. Красноярск, 1976. С. 46-59.
- Biberbach L. Analytische Fortsetzung. Berlin: Springer-Verlag, 1955, 240 p.
- Mittag-Leffler G. Sur la representation d’une branche uniforme d’une fonction monogene//Acta Math. 1905. No. 29. P. 101-182.
- Le Roy E. Sur les series divergentes et les functions d’efines par un d’evelopement de Taylor//Ann. Fac. Sci. Univ. Toulouse, 1990. No. 2. P. 317-430.
- Hardy G. H. Divergent series. Oxford: Clarendon Press, 1949, 503 p.
- Кук Р. Бесконечные матрицы и пространства последовательностей. М.: Физматгиз, 1960. 474 с.
- Рамис Ж.-П. Расходящиеся ряды и асимптотические теории. М.; Ижевск: Ин-т. комп. исслед., 2002. 80 с.
- Аракелян Н. У. Об эффективном аналитическом продолжении степенных рядов//Матем. сб. 1984. Т. 124, № 5. С. 24-44.
- Мураев Э. Б. Эйлеровское и борелевское суммирования рядов, их обобщения и приложения: дис. … д-ра физ.-мат. наук. Новосибирск, 1992. 364 с.
- Downarovich M. Analytic continuation of series of homogeneous polynomicals of n complex variables//Prace Mat. 1975. № 17. Р. 23.
- Arakelian N. H. Efficient harmonic continuation of the Laplace series//J. Contemp. Mathemat. Anal. 2012. Vol. 47, no. 3. P. 105-123.
- Яковлев Е. И. Аналог теоремы Окада//Вестник КрасГУ. 2006. № 9. C. 111-113.
- Яковлев Е. И. Об аналитическом продолжении кратного степенного ряда с помощью m-однородных полиномов матричным методом в обобщенную звезду Миттаг-Леффлера//Вестник СибГАУ. 2013. № 4(50). C. 87-92.
- Яковлев Е. И. Об аналитическом продолжении кратного степенного ряда с помощью одномерных матричных методов суммирования//Вестник СибГАУ. 2014. № 3(55). С.172-177.
- Znamenskiy S. V. Dokl. AN SSSR, 1975, Vol. 223, No. 3, P. 544-547 (In Russ.).
- Znamenskiy S. V. . O golomorffnykh funktsiyakh mnogikh kompleksnykh peremennykh. . 1976, Krasnoyarsk, IF SO AN SSSR Publ., P. 46-59.
- Biberbach L. Analytische Fortsetzung, Springer-Verlag, Berlin, 1955, 240 p.
- Mittag-Leffler G. Sur la representation d’une branche uniforme d’une fonction monogene, Acta Math, 1905, No. 29, P. 101-182.
- Le Roy E. Sur les series divergentes et les functions d’efines par un d’evelopement de Taylor, Ann. Fac. Sci. Univ. Toulouse. 1990, No. 2, P. 317-430.
- Hardy G. H. Divergent series. Oxford, Oxford, Clarendon Press, 1949, 503 p.
- Cooke R. G. Infinite matrices and sequence spaces. London, Macmillan, 1960, 473 p.
- Ramis J.-P. Raskhodyashchiyesya ryady i asimptoticheskiye teorii . Moscow, Izhevsk, Inst. comp. issl. Publ., 2002, 80 p.
- Arakelyan N. U. . Matem. sb., 1984, Vol. 124, No. 5, P. 24-44 (In Russ.).
- Muraev E. B. Eylerovskoe i borelevskoe summirovaniya ryadov, ikh obobshcheniya i prilozheniya: Dis. dokt. fiz-mat. nauk. . Novosibirsk, 1992, 364 p.
- Downarovich M. Analytic continuation of series of homogeneous polynomicals of n complex variables. Prace Mat., 1975, Z. 17, P. 23.
- Arakelian N. H. Efficient harmonic continuation of the Laplace series. J. Contemp. Mathemat. Anal, 2012, Vol. 47, No. 3, P. 105-123.
- Yakovlev Е. I. . Vestnik KrasGU. 2006, No. 9, P. 111-113 (In Russ.).
- Yakovlev Е. I. . Vestnik SibGAU, 2013, No. 4(50), P. 87-92 (In Russ.).
- Yakovlev Е. I. . Vestnik SibGAU, 2014, No. 3(55), P. 172-177 (In Russ.).


