О возможной динамике в модели ранжирования web-страниц PageRank и модернизированной модели расчета матрицы корреспонденций
Автор: Гасников Александр Владимирович, Гасникова Евгения Владимировна, Федько Ольга Сергеевна
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Математика, информатика, управление, экономика
Статья в выпуске: 2 (14) т.4, 2012 года.
Бесплатный доступ
Приводится основной аппарат, необходимый для исследования динамики макроси- стем (систем, описывающих динамику взаимодействия большого числа агентов) при больших значениях времени. В основе динамики лежит эргодическая марковская цепь с огромным числом состояний. При больших значениях времени распределение мак- росистемы по макросостояниям будет близко к стационарному. С ростом размерности макросистемы (количества состояний марковской цепи) стационарное распределение будет концентрироваться в окрестности наиболее вероятного макросостояния, которое и принимается за равновесное для данной макросистемы. В качестве примеров при- менения описанного формализма приводится вывод известного способа ранжирования web-страниц PageRank и вывод модернизированной статической энтропийной модели расчета матрицы корреспонденций исходя из «разумной» (индивидуально выгодной) динамики обменов местами жительства. В конце статьи приводится общая схема ис- следования равновесий макросистем, отличительной особенностью которой является возможность учитывать рост размерности пространства макросостояний системы вме- сте с ростом числа агентов.
Эргодическая теорема, функция ляпунова, энтропия, ранжирование web-страниц pagerank, гравитационная модель расчета матрицы корреспонден- ций, концентрация инвариантной (стационарной) меры, канонический скейлинг, усло- вие динамического равновесия, принцип детального равновесия
Короткий адрес: https://sciup.org/142185816
IDR: 142185816
Текст научной статьи О возможной динамике в модели ранжирования web-страниц PageRank и модернизированной модели расчета матрицы корреспонденций
После работ Е. Т. Джейнса (конца. 50-х годов XX века.) [1], А. Дж. Вильсона (конца. 60-х годов XX века.) [2], И. Пригожина с коллегами, Г. Хакена (70-е годы XX века.) [3, 4] в литературе достаточно прочно укрепилась концепция о плодотворности перенесения термодинамического формализма (см., например, [5-14] и цитированную там литературу) на различные макросистемы (в частности, встречающиеся в экономике, биологии, социальной сфере [2-4; 15-24]). В России систематические исследования в этом направлении были предприняты Л. Н. Розоноэром в начале 70-х гг. XX века. [25] (см. также [26-34] и цитированную там литературу). Упомянутая концепция часто используется для нахождения равновесия макросистемы. А именно, по аналогии с феноменологической термодинамикой, вводится вероятностное распределение на множестве состояний, в которых может пребывать макросистема. Такое распределение может, например, совпадать с инвариантной мерой эргодической динамической системы, порождающей рассматриваемую макросистему [11], или с финальным (равным стационарному) распределением эргодического (например, марковского) случайного процесса, порождающего рассматриваемую макросистему [35-40]. Если размерность макросистемы увеличивается, то, как правило, распределение сосредотачивается в окрестности наиболее вероятного макросостояния1. Таким образом, с ростом времени наблюдения за. макросистемой и размерности макросистемы следует ожидать нахождения макросистемы с большой вероятностью в малой окрестности наиболее вероятного макросостояния вне зависимости от того, в каком состоянии макросистема находилась сначала (иначе говоря, большую часть времени (иногда и просто на больших временах) макросистема будет пребывать в малой окрестности наиболее вероятного макросостояния). Естественно поэтому под равновесием макросистемы понимать наиболее вероятное макросостояние. Задача нахождения наиболее вероятного макросостояния часто сводится (асимптотически по размерности системы) к задаче максимизации энтропийно подобного функционала при ограничениях (в термодинамике таким образом можно получить статистики Больцмана, Ферми-Дирака, Бозе-Эйнштейна [1, 5]). Подробнее о приложениях этой концепции см., например, [1, 2, 30, 33; 41-45].2
В данной статье мы уделяем особое внимание тому случаю, когда эволюция макросистемы описывается законами стохастической химической кинетики (равноправие агентов) [47], причем число химических реакций и размерность пространства макросостояний системы могут расти с ростом числа агентов в системе. Но при этом, вообще говоря, не предполагается возможность осуществления термодинамического предельного перехода, т.е. не предполагается, что рост прямо пропорциональный [47, 48]. Часто мы будем считать, что число агентов должно расти быстрее, чем размерность пространства макросостояний.
Статья построена следующим образом. В разделе 2, по-видимому, впервые известная модель ранжирования web-страниц, положенная в основу работы поисковой системы Google в начале XXI века, обосновывается исходя из концепции равновесия макросистемы. В разделе 3 в ответ на запрос прикладников: предложить более адекватную модель расчета матрицы корреспонденций крупного мегаполиса (г. Москва), предлагается и обосновывается (с точки зрения концепции равновесия макросистемы) модернизация известной энтропийной модели, лучше описывающая реальные данные. В разделе 4 приведена общая схема, в которую ложатся модели, описанные в разделах 2 и 3.
-
1. Возможная динамика, приводящая в асимптотике (по времени) к новой интерпретации известного способа ранжирования web-страниц PageRank
Хорошо известно, что поисковая система Google была создана в качестве учебного проекта студентов Стэнфордского университета Ларри Пейджа и Сергея Брина [49]. В 1996 году они работали над поисковой системой BackRub, а в 1998 году на её основе создали новую поисковую систему Google [50]. В статье [49] был предложен определенный способ ранжирования web-страниц. Этот способ, так же как и довольно большой класс задач ранжирования возникающих, например, при вычислении индексов цитирования ученых или журналов, сводится к нахождению левого собственного вектора р1" некоторой стохастической матрицы Р; р1" = р^ Р. Обоснование этому дает теория цепей А. А. Маркова (1906). Точнее, эргодическая теорема для конечных однородных неразложимых и непериодических марковских цепей:
3! р1" : р1" = р1 Р, и если р1" (п + 1) = р1" (п) Р, п Е N, то
V р1 (1) ^ lim р1 (п) = р1 (здесь все векторы, являются распределениями веро- П >^
ятностей).
Цель настоящего раздела предложить другое обоснование ранжирующему вектору р ^ = р1 Р\ базирующееся на концепции равновесия макросистемы [47].
Имеется ориентированный граф G = (V, Е ) сети Интернет (вершины — web-страницы, ребра — ссылки: запись (г, j) Е Е означает, что на г-й странице имеется ссылка на j-ю страницу), N — число пользователей сети (это число не меняется со временем, N ^ |V| ^ 1),3 Р = (1 — а) Е + аР, где Е — единичная матрица, р^ = |{к : (г, к) Е Е }|-1, г = j, иначе = 0, а Е (0,1) (часто полагают а = 0.85). Пусть пг (t) — число посетителей web-страницы г в момент времени t. За один такт времени каждый посетитель с вероятностью ар,з переходит по ссылке на web-страницу д4 Считаем стохастическую матрицу Р неразложимой и апериодической. Ниже приведен основной результат, позволяющий по-другому интерпретировать вектор р (PageRank): р1 = рГР, согласно которому и происходит ранжирование web-страниц.
Теорема 1. V q = 0, ..., |V| 3 Xq > 0, Tq = O (Робу (| V|)) : V t > Tq
"(
Пк (t) - 1 Nрk
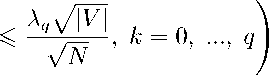
> 0.99 ;
V к = 0, ..., |V|, t > T q ^ P
3 X> 0, Т = O( Poly (|V|)) :
(
■ к ( t ) Np k
6 ХУЙ > 0.99 V N
где p1 = p1 P (решение единственно в классе распределений вероятностей ввиду неразло-эюимости). При этом здесь для удобства считаем pi > р2 > ... > рщ|.
Эффективный итерационный алгоритм поиска вектора p (PageRank), основанный на методе стохастического субградиентного зеркального спуска, описан в работе [51] (см. также [52]).
Рассмотрим теперь, следуя работе [53], другую (Network flow) модель, предложенную Дж. А. Томлиным в 2003 г., также описывающую распределение WWW-трафика. Далее с помощью формализма теории макросистем мы эволюционно проинтерпретируем статический способ ранжирования web-страниц, предложенный в [53], вводя разумную динамику и получая в равновесии желаемую статическую модель Томлина.
Обозначим через n^j (t) число пользователей WWW, которые в момент времени t находятся на web-странице д при этом каждый из них (независимо ни от чего) склонен перейти только на web-страницу j и делает это в промежутке времени [t, t + At) (при условии, что к моменту времени t > t он еще не перешел) с вероятностью XAt + o (At). При этом в момент перехода t пользователь с равной вероятностью выбирает, к какому классу njk (t), к Е V: (j,k) Е Е ему примкнуть.
{П * 3 }(t, J)es
что в некотором (уточ-
Далее описывается процедура построения такого
{П*'
ненном ниже) смысле, { n^j (t) } (^ j)eE
---→ t ^^
Определим множество A = { ntj }(t j)EE следующим образом:
-
1) 52 (г з) е ЕПгз = N = const — закон сохранения активности пользователей;
-
2) V г E V ^ ^^ (к i)GE riki = ^^ (i , ) G e nik — закон сохранения числа посетителей Тй страницы.
Заметим, что уравнения I, II линейно зависимы и, если забыть про ограничение целочисленности п^, то A — выпуклое (аффинное) множество с непустой внутренностью.
Заметим также, что |V| + 1 уравнения I, II, вообще говоря, не однозначно определяют I E | неизвестных { nij }(i j)GE’ поскольку |E| больше |V|, причем, как правило, в несколько раз (типично в пять, шесть раз). Для того чтобы определить < n* ■ > , введем
I (i,j)GE еще определение. Будем понимать под исходами всевозможные инъективные отображения 9 : {1,...,N} ^ E, такие что {nij = |{т : 9 (т) = (г, j)}|}(i j)GE E A. Предположим, что все исходы равновероятны. Тогда вероятность трафика {nij}(i j)GE E A Q R^1 есть
-1
,
P ({nij}(i, j)eE) = Z 1 ^N! I П nij! \ (i,j)GE где Z 1 - определяется из условия нормировки. Отсюда, с учетом формулы Стирлинга ln n! ~ nln (n/e) (обоснование см. ниже), имеем
In р {^ГЫ} }(i, })ge) ^ Е nij ln (nij /e) . (i, j)GE
Таким образом, поиск наиболее вероятного трафика сводится к задаче максимизации энтропии
Н ^{nij}(i, })ge) = — Е nij ln nij
(i,j)GE на неотрицательном ортанте R^1 при аффинных ограничениях A.
Положим
V (г, j) EE ^ pij =nij/N.(1)
Считая
N »|E| > |V|> 1,(2)
«забудем» далее про рациональность Pij.
В результате приходим к задаче энтропийно-линейного программирования (*):
Н №\i,3)Ge) = - Е PH ln Pi3 ^ max.
(i, j) G E { Pii } (.i,j )e B G A A
-
A: E Pij =1, E Pki - E Pik = 0,г E V.
(i, j) G E k. (k, i) G E k. (i, k) G E
Из формул (1), (2) и того факта, что решение задачи (*) достигается во внутренней
IEI точке множества A Q R^ основной вклад в сумму Стирлинга было «вполне
Поясним теперь, чем
[2], следует, что V (г, j) E E ^ nij ^ 1 для слагаемых, дающих ln Р ^{nij}(i j)GE^, т-е- применение асимптотической формулы законным».
примечательно наиболее вероятное распределение |P*'^. .^
трафика. Оказывается, в предположении равновероятности всех исходов, возникать будут в основном те распределения { Pij }(i j)GE E .A Q R^1, которые «близки» к {p*'} (обоснование см. в разделе 4).
Вернемся к задаче (*). Её решение можно явно выписать (см. раздел 4):
V (г, j) E E ^ Pij = exp (-Aq) exp (-Ai) / exp (-Aj), где Ад - множитель Лагранжа (двойственная переменная) к ограничению ^(щ j)eE Pij = 1 а Ai — множитель Лагранжа к ограничению ^k: (k ^epki — ^k. (i k)eE Pik = 0- Приведенную связь можно интерпретировать как наличие у web-страниц «потенциалов значимости» — рангов тгг, определенных с точностью до одного и того же положительного множителя:
Г = exp (—Аг) — «Температура» (HOTness) г-й страницы.
Чем больше «температура» web-страницы с номером г и чем меньше «температура» web-страницу с номером j ((г, j") Е Е), тем интенсивнее поток Pij (тем больше пользователей переходит в единицу времени с web-страницы г на web-страницу j).
Важно обратить внимание на общее правило: полученное попутно (при поиске равновесия макросистемы, путем решения задачи энтропийно-линейного программирования) решение двойственной задачи будет представлять самостоятельную ценность. Это обстоятельство хорошо известно в математической экономике (интерпретация Л. В. Канторовича множителей Лагранжа (двойственных переменных) к ресурсным ограничениям как цен ресурсов [54]) и в статистической физике (например, при выводе статистик Л. Больцмана, Ферми-Дирака, Бозе-Эйнштейна [5, 8, 9]). При этом возникающие в статистической физике множители Лагранжа также получают впоследствии интерпретацию и размерность, например, величина, обратная к температуре [5]. Используя эту аналогию, Дж. А. Томлин предложил ранжировать web-страницы (в поисковой системе) по их «температуре». Более посещаемые web-страницы «нагреты» сильнее, как следствие, имеют больший ранг.
Сформулируем теперь более аккуратно основной результат. Для этого предварительно введем такую перестановку ij (•), что P * j(1) > P*j(2) > ••• > P*j(|E|) ’ а затем введем обозначение пк (t) = nij(k) (t), к = 1, •••, |Е|.
Теорема 2. V q = 0, „•, |Е| 3 Aq > 0, Tq = O (Poly (|П|)) : V t > Tq
/ Ik (t)
Np*,x \ rtJW
6 A q ^ Ж , к = 1, _ q^ > 0^99; Vn
3 A> 0, T = O (Poly (|K|)) :
∀
к = 0, •••, |Е| , t > T ^ P
ik (t) - 1
P* j ( k )
6 ДВ > 0,99 Vn
Рассмотрим теперь общую задачу энтропийно-линейного программирования:
т
— ^Xk ln (xk /е) k =1
^ max ;А:Л ( x ) = q — Tx = 0 / ,F (5) = 5 — Gx > (L Д ел n R+
В работе [55] для отыскания единственного решения (3) было предложено семейство двойственных барьерно-мультипликативных итерационных алгоритмов, которое содержит алгоритмы Брэгмана-Шелейховского, MART, GISM, Ю. С. Попкова и др. [30, 45]:
Xk = exP (— Е Р =1 t pk Ар — Е =1 9qkPq^ , к = 1 •••, т;
* А ” +1 = A k — дд* (qp — Е т=1 t pk XV, P = 1,•••,l; N:
. ^k+1 = pk — аРкдч (dq— Em=i gqkxk), q = 1 •••Еш, где шаги д > 0, a > 0 достаточно маленькие, а дважды гладкие функции [д* (• )}Р=1, {gq (• )}™=1 монотонно возрастают и равны нулю в нуле. Например, часто выбирают дР (y) = — ln (1 — y/qp) ep = 1,•••,l;gk (y) = y/dq,q = E-,^
Однако, как правило, разумно (с точки зрения эффективности счета) обнулять на каждом шаге большую часть случайно выбранных компонент этих векторов, причем вероятностный отбор осуществляется исходя из текущего состояния итерационного процесса (отметим, что согласно алгоритму Кнута-Яо [56] задача разыгрывания случайной величины, принимающей п различных значений, требует в среднем log2 (i — 1) +2 подбрасываний симметричной монетки, значит, может быть довольно быстро решена), при этом после обнуления большинства компонент и соответствующего вытягивания по оставшимся (чтобы сохранить приблизительно длину) получившейся вектор должен быть довольно близким к градиенту [57]. То есть разумно осуществлять в двойственном пространстве своеобразный стохастический субградиентный спуск (для более глубокого погружения в эту тематику можно рекомендовать работы А. С. Немировского [58] и Ю. Е. Нестерова [59]).
Глобальная сходимость итерационного процесса (4) была установлена в [55] при следующих предположениях:
-
1) 3 z > 0т : q — Т z = 0/, d — Gz > 0w;
-
2) Строки матриц Т = \\ tpk ||pm=i и G = I gqk ll^imi линейно независимы в совокупности.
При этом было замечено, что предположение 2 не всегда выполняется в прикладных задачах (см., например, модель ранжирования web-страниц Дж. А. Томлина). Оказывается, что от предположения 2 можно отказаться. А именно, если справедливо только предположение 1, то найдутся такие достаточно маленькие шаги (в зависимости от начального приближения), что итерационный процесс (4) будет сходиться (глобально, поскольку начальное приближение может быть любым допустимым ограничением задачи) к единственному решению задачи (3). Доказательство в целом аналогично случаю регулярных ограничений. Однако в случае зависимых ограничений решение двойственной задачи, вообще говоря, будет не единственно (более того, множество решений будет представлять собой линейно-выпуклое множество). Поэтому исследовать итерационный процесс следует в должным образом факторизованном пространстве.
Итерационные алгоритмы (4) особенно эффективны:
-
• для сильно разреженных матриц Т и G;
-
• при I + w ^ т.
-
2. Возможная динамика, приводящая в асимптотике (по времени) к новой версии статической модели А. Дж. Вильсона расчёта матрицы корреспонденций
При этом время работы (число арифметических операций типа умножения двух чисел с плавающей точкой) детерминированного алгоритма (4) оценивается соответственно как O (т + I + w) и O (т • (Z + w)). Стохастические варианты, о которых мы говорили выше, работают заметно быстрее.
В некотором городе имеется п районов, Lt > 0 — число жителей Аго района, Wj > 0 — число работающих в j-м районе (число рабочих мест), xtj (t) > 0 — число жителей, живущих в i-м районе и работающих в j-м в момент времени t > 0. Со временем пронумерованные жители (количество которых не меняется5 и равно N = -3 i Lt = ”21= 1 Wj) меняют места жительства (квартиры). Считается, что отмеченные изменения могут происходить только за счёт обмена квартирами, т.е.
xtj (t) > 0, ^”= 1 xtj (t) = Lt, ^”= 1 xtj (t) = Wj, i,j = 1, ..., n, 1 « n2 « N. (A)
Пусть в момент времени t > 0 r-й житель живет в к-м районе и работает в т-м, а s-й житель живет в р-м районе и работает в q-м. Тогда Хк т. p q (t) At + о (At) есть вероятность того, что жители с номерами г и s (1 6 г < s 6 N) поменяются квартирами в промежутке времени (t,t + At). Естественно считать, что вероятность в единицу времени обмена местами жительства зависит только от мест проживания и работы обменивающихся.
Например, можно считать, что расстояние от района г до района j есть lij > 0, а
Xk,m; p,q (t) = X^ p,q = XN -1 exp ( R (lkm) + R (lpq ) - (R (lpm) + R (lkq )) ),
V ^- -/ v - - У суммарные затраты суммарные затраты до обмена после обмена где X > 0 характеризует интенсивность обменов, функция R (l) = (al^ — ш ln l) /2, a > 0, 3 > 0, ш > 0 отражает затраты в пути (первое слагаемое) и одновременно возможность найти подходящую работу на расстоянии порядка l от места жительства: чем больше l, тем больше территория для поиска ~ 2тг1А1, тем больше вероятность успеха (найти подходящую работу), тем меньше должны быть затраты R (l) (второе слагаемое). Анализ данных по г. Москва (на базе опыта А. В. Кулакова (МАДИ)), проведенный осенью 2011 г. в Лаборатории прикладного моделирования транспортных систем ИПМ им. М. В. Келдыша РАН (зав. лаб. В. П. Осипов), показывает, что ш ~ 2 — 4 (надо заметить, что эта оценка предварительная и нуждается в перепроверке). В классической статической энтропийной модели (второй половины 60-х годов XX века) А. Дж. Вильсона ш = 0 [2, 32, 47]. Однако по Москве наблюдается заметно лучшее соответствие реальных данных рассматриваемой модели, если допускать ш > 0 и оптимально его подбирать. При весьма общих предположениях считают, что 3 ~ 1- По повод у выбора a см., например, [32]. Отметим также, что ряд специалистов по расчету матрицы корреспонденций (например, В. И. Швецов (ИСА РАН)), с которыми мы консультировались, склонны считать, что вместо слагаемого al^ в формуле для R (l) правильнее писать:
f
al^,
0
V > ш,
al^ = v In l,
[ V ln l, l > l,
Можно показать (см. раздел 4), что
V {xij}n= i ,=1 € (A) ^ lim Р (x^ (t) = xij, i,j = 1, ...,n) = , t—^c n, n
= Z -1 П exp
((
ш In li j
— a • (l ij /} Hj^ • ( Xij !) 1 ^ p {{Xij} n= n , j=J ,
где статсумма Z находится из условия нормировки получившейся «пуассоновской» вероятностной меры. Отметим, что распределение p ({x^}"= П j=1) удовлетворяет условию детального равновесия (частный случай более общего условия инвариантности):
(xkm + 1) (xpq + 1) p ({x11, ..., xkm + 1, ..., xpq +1,..., xpm 1, ..., xkq 1, ..., xnn}) Xk,m; p,q — xpmxkq p
({xy ft ft=1)
X p,m ; k,q.
Распределение p ({x^}П=П j=1) на множестве (А) сконцентрировано при N ^ 1 (см. раз-n, n дел 4) в окрестности наиболее вероятного значения < x* 1 , которое находится, как ij i=1,j=1
решение задачи энтропийно-линейного программирования (по поводу ограничения целочисленности { xij }n=n j=1 см- Р, 47] и предыдущий раздел):
n, n n, n xij ln(xij/е) +
(a • (lij У
— ш ln li j xij ^ min .
7 {^j )Г= r,,-=xe(A)
Решение задачи (5) можно представить как xij = exp
(—1 — Xi
— Х У + ш ln lij - a ^ (lij ) ^ ) ,
где множители Лагранжа (двойственные переменные) {X ('}[(_! и
■}” _
из равенств системы (А). На практике мы имеем информацию о {Li, Wi}n_1
Решив задачу (А), мы найдем
определяются и {lij V ^р
{хкт ({L^W^ ;
{ lij К^х)}
п, п к=1,т=1
Такой способ расчета матрицы корреспонденций с ш = 0 в литературе часто называют (энтропийной) гравитационной моделью;
хц = AiBjLtWj (lijГ exp (—а • (lij^ , где {Ai}n_1 и {Bj}п_1 определяются из соотношений, аналогичных [2, 30, 32]:
-1 п \
E Bj Wj (lij)ш exp --а • (lij ^ I j_1
( п
E г_1
АгТг
х -1
(lij)ш exp ( -а • (lij /) )
Приведем теперь оценку концентрации стационарного распределения р
окрестности наиболее вероятного значения такую перестановку ij (•). что x*j(1) > x*j(2)
{ х
п, п i_1,j_1
(щап^ф
В
. Для этого предварительно введем
> ... > х *,(п 2 ), а затем введем обозначение
nk (t) = Xij(k) (t) ,к = 1,..., n2.
Теорема 3. V q = 0, ..., n2 В Xq > 0, Tq = O (Poly (N )) : V t > Tq
/ Пк (t) \ X *j ( k )
-
Xq n
6 vN, к =1, ‘"’q)
> 0.99;
В X > 0, T = O (Poly (N )) :
V к = 0,
.., n2, t >T - P
(
Пк (t) Xij(k)
-
Xn
6 V N
^ > 0.99.
Стоит обратить внимание, что выше был описан лишь один из возможных способов (энтропийный) получения модели расчета матрицы корреспонденций. Существуют и другие подходы. Например, модель С. А. Стауффера [61], также называемая моделью промежуточных возможностей, и модель конкурирующих центров [62, 63]. Хотелось бы также обратить внимание на предложенную в статье [64] объединенную «гравитационно-конкурирующую» модель энтропийного типа. Примечательно, что обоснование таких популярных на практике моделей может быть получено подобно только что изложенной схеме, где в стохастическую динамику вводится больше специфики, в частности, вводится учет новых факторов, определяющих формирование корреспонденций [32].
В последнее время в крупных мегаполисах крайне остро встают вопросы о том, какие меры надо предпринимать, чтобы разгрузить автотранспортную сеть города. Например, важно уметь отвечать на следующие вопросы: где и какую дорогу следует построить при заданных бюджетных ограничениях? Каким образом (в каком размере) взимать плату за проезд с трасс в центре города? На каких трассах стоит в первую очередь увеличивать число полос? Где стоит в первую очередь переделывать развязки - делать новые? Ниже (на базе модели расчета матрицы корреспонденций) мы приведем (мотивируя и аргументируя) некоторый математический аппарат (оставаясь в рамках того же формализма, в котором мы изложили предыдущие примеры), который может пригодиться в изучении описанных выше вопросов [32, 47, 65, 66].
Ориентированный граф Г = (К, Е) — транспортная сеть города (К — узлы сети (вершины). Е CV х К - дуги сети (рёбра графа)). Пусть W = {w = (i,j) : i, j E К} — множество пар источник—сток; р — {«1, «2, ..., vm} — путь из «1 в vm, если (v^,Vk+1) € Е, к — 1,..., т — 1, т ^ 1 (как будет видно в дальнейшем (см. пример В. И. Швецова), иногда для задания пути может быть недостаточно указания только набора вершин, в общем случае нужно также указывать, какое именно ребро, соединяющее заданные вершины, выбирается); Pw — множество путей, отвечающих корреспонденции w € W; P — Uwew P™ ~ совокупность
всех путей в сети Г; жр — величина затраты на проезд по пути р, G (ж)
у е — ^р е р 6 ер ж р, Г Де 6 ер —
1,
0,
потока по пути р. ж — {жр : р € P }• Gp (ж) — удельные — { G p (ж) : р € P }: уе — величина потока по луге е:
е Д "' ®— ' ■
те (уе) ~ удельные затраты на проезд по дуге е (как правило, возрастающие, выпуклые, гладкие функции), естественно считать, что Gp (ж) — ^2ееЕ те (уе) 5ер (G (ж) — ©г т (у)). Заметим, что в приложениях часто требуется учитывать и затраты на прохождения вер-
шин графа (в свою очередь эти затраты могут зависеть от величин всех потоков, по путям, проходящим через рассматриваемую вершину) [32]. Пусть также известна матрица корреспонденций dw, w € W (см. предыдущий пример). Тогда вектор ж, характеризующий распределение потоков, должен лежать в допустимом множестве:
X — ж > 0 :
жр — dw , w € W > . р е Р ш
Это множество может иметь и другой вид, если дополнительно учитывать, например, конечность пропускных способностей рёбер (ограничения сверху на уе).
Рассмотрим игру, в которой каждому элементу w € W соответствует свой, достаточно большой ( dw ^ 1). набор одно тинных «игроков» («сидящих на корреспонденции w»). Множеством чистых стратегий каждого такого игрока является Pw, а выигрыш (потери со знаком минус) определяется формулой — Gp (ж) (игрок «выбирает» путь следования р € Pw, при этом он пренебрегает тем, что от его выбора также «немного» зависят |PW| компонент вектора ж и, следовательно, сам выигрыш — Gp (ж)). Можно показать, что отыскание равновесия Нэша(-Вардропа) ж* € X (макроописание равновесия) равносильно решению задачи нелинейной комплементарности (принцип Дж. Г. Вардропа (1952)), что равносильно решению вариационного неравенства:
V w € W,
р € Pw ^ ж р • G ^ p (Т*) — min Gq (ж*))
— 0 О V т € X ^(с (ж*) , (т — ж*)^ > 0.
Несложно показать, что если G (т) — строго монотонное преобразование, т.е.
V ж, Т € X (ж — z) ^ (б (т) — (5 (Т), Т — Т^ > 0, то равновесие Нэша-Вардропа единственно. Также несложно показать, что задача отыскания равновесия Нэша-Вардропа сводится к решению следующей задачи выпуклого программирования:
Ф(ж) — £ /
ЕЕ 0°
КреР ХР^ер те (z) dz ^ min.
х е х
Отсюда видно, что если
V е € Е ^ Те ( • ) > 0, TO V (у) — ^еЕ Jo" те (z) dz
-
— строго выпуклый функционал, и равновесие у * — единственно. Отметим, что это еще не означает единственность равновесия ж*. Действительно, при весьма естественных условиях вектор-функция удельных затрат пользователей на проезд (5 (ж) может не быть строго монотонной:
-
3 ж,у € Х (ж — у): G (ж) — G (у) ^ ^ (ж) — G (у), ж — у) — 0.
Связано это может быть, например, с тем, что G (ж) = 0Т т (у) у = 0ж, где вектор У = {Уе}еЕЕ описывает загрузку ребер (дуг) графа транспортной сети, т (у) = {те (Уе)}ееЕ — вектор-функция затрат на проезд по ребрам графа транспортной сети, 0 — матрица инцидентности ребер и путей, и разные векторы распределения потоков ж могут соответствовать одному и тому же вектору у = 0ж.
Пример (пенсне Швецова). На рис. 1 показано равновесное распределение потоков для любого значения параметра ж G [0, 0.5] и любой строго монотонной функции затрат, одинаковой для всех дуг графа.
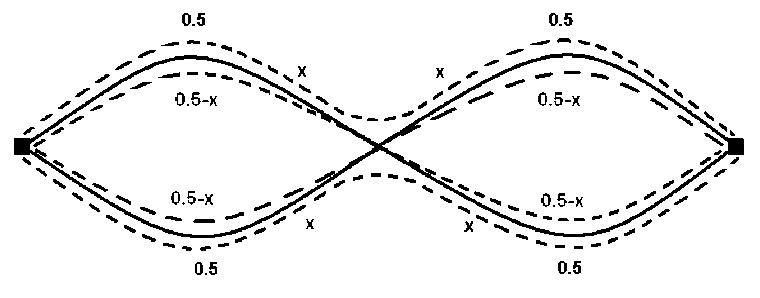
Рис. 1
Численные методы поиска равновесного распределения потоков описаны, например, в работах [32, 47]. Отметим среди этих способов один из первых: итерационный алгоритм Франка-Вульфа. Примечательно, что этот численный алгоритм, впрочем, как и ряд других, может быть содержательно проинтерпретирован (как динамика нащупывания равновесия Нэша в соответствующей повторяющейся игре) подобно приведенному ниже тексту. Далее мы приводим способ взаимодействия участников дорожного движения (игроков), приводящий к стохастическому равновесному распределению потоков [67], «вырождающемуся» в равновесное распределение Нэша-Вардропа.
Предположим, что свой путь на (п + 1)-м шаге6 игрок, сидящий на корреспонденции w, выбирает согласно смешанной стратегии (в независимости от всех остальных): с вероятностью
Probp (п + 1) = у exp(— Gp (ж (п))/Т ) / Z™, w G W, (6)
выбрать путь р G Pw (0 < у 6 1. у — маленькое), а с вероятностью 1 — у действовать согласно стратегии, использованной на предыдущем п-м шаге. Здесь жр (п) — количество игроков, сидящих на корреспонденции w и выбравших на п-м шаге стратегию р G Pw,
Z^ = £ exp(—Gp (ж (п))/Т), р- Р.
Т > 0 — «температура» (горячность) игроков. Это хорошо известное logit-распределение [47]. Оно может быть проинтерпретировано, как выбор каждым игроком наилучшей стратегии вчерашнего дня, если игрок «переносит» затраты вчерашнего дня Gp (ж (п)) на день сегодняшний, но допуская при этом случайные флуктуации Gp (ж (п)) + £р, г де Рр — независимые случайные величины, имеющие одинаковое двойное экспоненциальное распределение (Гумбеля). Тогда arg min {Gp (ж (п)) + £р} как раз имеет указанное выше logit-реРш распределение.
Теорема 4. Пусть М е G Е ^ те (•) > 0 и жр > 0 ^ жр ^ 1. Тогда стохастическая марковская динамика (6) «сходится» на больших временах к некоторому стационарному распределению вероятностей, которое называют «стохастическим равновесием в транспортной сети». В предположении, что Т > 0 и 7 > 0 — долмсным образом малы, это стационарное распределение сконцентрировано в малой окрестности такого равновесия Нэша -Вардропа:
х* = arg min У' У (хр ln (хр/ IPW |) - Хр) , ж Е У : ©ж=у *
-
У w E Wp E Pw
где X _ единственное решение задачи
Уе
V (У) = У / Те (z) dz ^ e E E 0
min . у=©ж, x E X
Эта теорема отвечает на некоторые вопросы, поставленные в работах [68, 69].
Отметим, что предложенную динамику (6) можно трактовать как стохастическую динамику наилучших ответов в эволюционной (популяционной) игре [70-72], при этом полученное равновесие может также быть проинтерпретировано как «quanta! response equilibria» [73]. Близкой к предложенному итерационному процессу (6) является концепция генетических алгоритмов [74] и эффективный приближенный вероятностный (с гиббсовским («logit») распределением вероятностей) алгоритм Григориадиса-Хачияна [75].
Довольно близкое к теореме 4 утверждение имеется в недавней работе [76]. Отметим также работы [77, 78], в которых предлагается схожая с (6) содержательная стохастическая динамика на базе стохастического субградиентного зеркального спуска, которая почти наверное приводит к равновесию Нэша-Вардропа.
Описанный выше формализм позволяет пойти и дальше. В частности, рассмотреть модели равновесного распределения для нескольких классов пользователей (в том числе модели расщепления потоков по типу передвижений), модели равновесного распределения потоков с переменным спросом на потоки, динамические модели равновесного распределения [32, 69]. На счет последнего, пока имеющийся здесь задел совсем не велик, и работа в этом направлении является, на наш взгляд, сейчас наибольшим вызовом в этой области.
Отметим также, что описанная выше модель равновесного распределения потоков (BMW-модель [47]) хотя и является очень популярной (достаточно сказать, что эта базовая модель, зашитая практически во все наиболее популярные сейчас пакеты моделирования транспортных потоков: ЕММЕ/3, MITSIM, PTV(VISSUM), TRANSNET, AIMSUN и др.), тем не менее у неё есть и свои довольно существенные недостатки, о которых, например, написано в статье [79]. В этой же статье была предложена оригинальная модель равновесного распределения потоков (менее требовательная к качеству располагаемых данных), получившая впоследствии название модели Нестерова-де Пальмы или модели стационарной динамики. В [47] описан способ вычисления стохастических равновесий в этой модели. Здесь мы бы хотели лишь отметить, что, так же как выше для BMW-модели, можно было провести соответствующие рассуждения и для модели Нестерова-де Пальмы.
В заключение этих двух разделов хотелось бы также упомянуть то обстоятельство, что в довольно большой класс математических моделей в биологии может быть введена динамика подобно описанным выше примерам [15]. При этом интересно отметить, что введенная динамика получает содержательную интерпретацию: «естественный отбор». С помощью функционалов Ляпунова такой динамики формулируются условия «эволюционной оптимальности». В этой связи можно рекомендовать работы В. Н. Разжевайкина, см., например, [80] и цитированную там литературу.
3. Общая схема исследования равновесий макросистем
Ниже приводится (во многом под влиянием работ [18, 19, 47, 48, 81-83]) общая схема (в непрерывном времени), в которую «ложатся» примеры разделов 2 и 3.
Предположим, что некоторая макросистема может находиться в различных состояниях, характеризуемых вектором n с неотрицательными целочисленными компонентами. Будем считать, что в системе происходят случайные превращения (химические реакции). Пусть n ^ n — а+Д, (а, Д) е J — все возможные типы реакций. Введем, следуя М. А. Леонтовичу (1935) [19], интенсивность реакции (случай дискретного времени рассматривается аналогичным образом):
А( щД ) ( п ) = а ( й,Д ) (п '"' — а + Д) = М 1 ^ск д ( п ) П " ' •... •(n . — а. + 1 ,
г : а > 0
где К ? > 0 — константы реакции (в химической кинетике — постоянные, а в социодинамике (В. Вайдлих [20]) — необязательно); при этом часто считают . n. (t) = М, т.е. A^cg) (n) — вероятность осуществления в единицу времени перехода n ^ n — а + Д в единицу времени равновероятно выбираются («приближение среднего поля») любые два жителя города и в зависимости от того, в каких состояниях они находились, «случайно» переводятся в новые состояния. На макроуровне все это соответствует принципам химической кинетики (закон действующих масс Гульдберга-Вааге, 1864 [18]). Таким образом, динамика макросистемы задается линейной полугруппой (однородный дискретный марковский случайный процесс), инфинитезимальный оператор которой определяется интенсивностями реакций А(^д) (n).
Следующая теорема отображает (немного обобщая) известные результаты а) В. В. Веденяпина [18], б) С. А. Пирогова, В. А. Малышева, А. Н. Рыбко [19, 81] и в) обобщает результаты В. Вайдлиха и др. [20] на случай, когда рассматривается более общая схема, чем модель миграции населения.
Теорема 5. а) (Д, n (t)) = (Д, n (0)) О Д±Ып ] а — Д>, . .(inv).
(a,P)eJ
б) Пусть выполняется условие динамического равновесия, которое, следуя В. В. Веденяпину, будем далее называть условием Штюкельберга-Батищевой-Пирогова:
3 е > 0 :
Гогда «пуассоновская» мера v (П) = И. А У е
к с п е? = Е« кс1кI п е ^к с(П) = кау (шбп)
pYY3s3 ^g . ( c,g ) eJ aYY3s3 \ ^ \ j g) \ ;
Xi[пУ (точнее говоря, мера, индуцирован-
пая пуассоновской мерой на множестве (вообще говоря, конечном!), задаваемом условиями (inv)), где А . = е.М, а У* — произвольное решение (ШБП), будет инвариантной относительно предложенной стохастической марковской динамики. Эта мера экспоненциально быстро концентрируется, с ростом М, в окрестности наиболее вероятного состояния (также удовлетворяющего условию (ШБП)), которое и принимается за положение равновесия макросистемы. Задача поиска наиболее вероятного макросостояния асимптотически эквивалентна задаче максимизации энтропийного функционала (воспользовались n! = V 2ттп (п/е)п (1 + о (1)) — формулой Стирлинга);
Е ( п ) - УД n. • (ln(n . /A . ) г
— 1)
на множестве, задаваемом условием (inv). Отметим, также условием унитарности [19], обобщает хорошо условие детального равновесия [20, 38]:
что условие (ШБП), называемое известное в физике и экономике
3 е > 0 :
V ( а, Д ) е
J ^ кШ е ? = кШ У.
3 3
в) Пусть
V (Й,Д) е J ^ £ а . = г
Е Д . ;
г
а.,Д е {0,1} , K ?
-*
Kg, с ,
Кд (П) = Кд exp I ^ Hi ( п , + 1) - ^ "' ( п , ) I ■ H ( п , ) 6 °’ \i: p t =1 i: а,=1 /
Тогда мера v (П) = exp (^ U , ( п , )) • Hi ( п , !)-1, где lA. ( п , ) = 2 ^П= 1 h , (v) будет инвариантной относительно предложенной стохастической марковской динамики. Эта мера экспоненциально бистро концентрируется, с ростом М = ^Z, п, (t), в окрестности наиболее вероятного состояния, которое и принимается за положение равновесия макросистемы. Задача поиска наиболее вероятного макросостояния асимптотически эквивалентна задаче максимизации энтропийного типа функционала
Е (П) ~'22 {-пг ln (п,) + Ui (п,) } i на множестве, задаваемом условием (inv).
Замечание б) и в). В пунктах б) и в) предполагалось, что марковский процесс неразложим (неприводим) в классе (inv): из любого состояния можно со временем прийти в любое другое (по-прежнему оставаясь на множестве (inv)). Отсюда следует единственность инвариантной меры. Это условие не выполняется, например, для хорошо известной модели «хищник-жертва» (кролики-трава) [3, 15, 17, 22], в которой имеется поглощающее состояние: без хищников.
Замечание б). Будем считать, что ограничения (законы сохранения) (inv) задаются СЛАУ Ап = d, где А = \\Аы|| - матрица максимального ранга. Обозначим через A множество неотрицательных целочисленных векторов П, удовлетворяющих Ап = d. Тогда равновесие п* = {п*}”1 находится как решение задачи Е (П) ^ max (поскольку функционал пЕА строго вогнутый и считаем п* ^ 1, то целочисленностью переменных можно пренебречь, то есть произвести релаксацию задачи). Используя принцип Лагранжа, можно показать, что решение этой задачи представляется в виде
п * = п , (у*) = Ai exp
(^А^) ■
где двойственные переменные (множители Лагранжа) у* определяются из системы Ап (у) = d. Исследуем концентрацию меры р ( { п , } ” 1) в окрестности наиболее вероятного значения { п * }” 1- Для этого прежде всего за .метим, что из определения { п * }” 1 следует
V 1 I” д^\Д д ln р ({ п * } ” 1) (
V {ni}i=1 € (A) ^ / v дп • ( п * - п , ) 6 °’
i
Поэтому
V { п , }”1 € (A) 3 9 € [°, 1]:
т lnр({п*}т=1) 6 lnр (н*}”^)+ £ i=1
д2 ln р { {п^ + п* • (1 - 9)}”=^ дп?
2 (Ду-Д*)
довольно общих предположениях, как O (poly (М)). Отсюда получаются соответствующие оценки в теоремах 1 и 3. Причем, как показали результаты численных экспериментов, возникающие там полиномы имеют невысокую степень (O (poly (М)) = O (М)). Открытой задачей является оценка mixing time в общей схеме М. А. Леонтовича. Перспективным в этой связи представляется использование некоторых конструкций работ [87, 88].
Отметим, что ряд моделей разделов 2 и 3 демонстрируют ситуацию, когда число со стояний (т = dim п) и число реакций (| J|) растут вместе с ростом числа агентов М . Это обстоятельство, равно как и зависимость К^ (п), не позволяют напрямую использовать аппарат, разработанный в [18, 19, 47, 81-83], связанный с анализом системы обыкновенных дифференциальных уравнений, возникающей при каноническом скейлинге (М 4 то так, что 3 limM>го п (0) /М = с > 0) стохастической марковской динамики. Отметим также, что в приведенных выше рассуждениях нам даже не потребовалось существование при термодинамическом предельном переходе М 4 то, |J| 4 то «ненулевого» («близкого к равномерному») финального распределения [89, 90]. Как следствие концентрация получилась не такая плотная, как в моделях, в которых это условие выполняется (см., например, модель Вильфредо Парето «Кинетика социального неравенства» [23,47, 91]).
Контрпример б) (С. А. Пирогов). Условие (ШБП) является только достаточным условием инвариантности «пуассоновской» меры. Действительно, рассмотрим систему уравнений химических реакций (константы реакций К одинаковы и постоянны):
А + В* 4 А* + В-В + С * 4 В* + С С + А* 4 С * + А, причем пд (t) + пд* (t) = пв (t) + пв* (t) = пс (t) + пс* (t) = N .
Заметим, что есть и еще один независимый закон сохранения:
пд (t) + пв (t) + пс (t) = const.
Можно проверить, что «пуассоновская» мера (« —» — знак пропорциональности)
v (п) - С. • ■ • • С. - (1^е-1/пд!) • ... • (1И^* е-1/пс*!)
будет инвариантной, хотя условие (ШБП), очевидным образом, не выполняется.
В связи с этим контрпримером заметим, что понятие равновесия макросистемы «не завязано» на условие (ШБП). Так, в контрпримере С. А. Пирогова равновесие будет существовать:
пд (то) та пд * (то) та пв (то) та пв * (то) та пс (то) та пс * (то) та N /2.
Утверждения теорем 2 и 4 не ложатся в рамки теоремы 5. Чтобы лучше понять, каким образом эти теоремы могут быть получены, приведем другой подход.
Если в первом подходе мы сначала делали предельный переход по времени (стремится к бесконечности), а потом по числу агентов (стремится к бесконечности), то во втором подходе предлагается осуществить предельные переходы в обратном порядке.
Предположим теперь, что множество J не зависит от М, и в начальный момент времени для любого г существует предел с (0) = lim п^ (0) /М, К “ (п) := К “ (п/М ). Тогда м >го ^ ^
(Малышев-Пирогов-Рыбко [81]) в произвольный момент времени t > 0 и для любого г существует предел по вероятности (заметим, что п^ (t) — случайные величины, тем не менее Сг (t) - уже не случайные величины) с (t) п=' lim щ (t) /М. Описанный выше приём назым ^го вается каноническим скейлингом. В результате такого скейлинга приходим к «динамике квазисредних» (терминология В. Вайдлиха [20]):
^ = Ефд^ (Зг - «г) К (С) П, ДУ (ДК)
Эти же уравнения можно получить и по-другому. А именно, как приближенную динамику средних сг (t) = Е [щ (t) /М]. Приближенную в том смысле, что при выводе (ДК)
используется приближение: F (Ci (t)) ~ Е [F (г (t) /М )] для «достаточно хороших» функций F (например, полиномов). Это верно в случае пикообразного распределения i (t).7
Можно показать [18, 82], что если выполняются условия (ШБП), то траектория (ДК) сходится к неподвижной точке (какой именно, зависит, вообще говоря, от «точки старта»; но можно сказать и точнее: к той единственной неподвижной точке из семейства неподвижных точек, которая принадлежит аффинному многообразию (inv), инвариантному относительно (ДК)).8 Для этого вводится (минус) энтропия: Н = ^Д Ci • (ln (ci/^i) — 1) и показывается, что она является функцией Ляпунова для системы (ДК). Обратим внимание, что инвариантная мера (при каноническом скейлинге) «породила» функцию Ляпунова (см. п. б) теоремы 5). Эта не случайно. Подобные закономерности наблюдаются для рассматриваемых моделей и без условия (ШБП), и даже без предположения о том, что инвариантная мера концентрируется около единственного положения равновесия, то есть аттрактором может быть множество куда как более сложной структуры.
Естественно (в виду примера С.А. Пирогова) теперь задаться над вопросом: а что будет, если условия (ШБП) не выполняются, однако система (ДК) имеет на внутренности пересечения неотрицательного ортанта и инвариантного аффинного многообразия (inv) единственную неподвижную точку? Оказывается, имеет место
Теорема 6. Если эта точка экспоненциально глобально устойчива, то 1) все законы сохранения (ДК) определяются (inv)' 2) около положения равновесия инвариантная мера будет экспоненциально бистро концентрироваться (с ростом М); 3) скорость сходимости к равновесию (mixing time [84]) оценивается как O (poly (М)); 4) элементы корреляционной матрицы случайного вектора г (t) равномерно ограничены по времени; 5) предельные переходы lim и lim перестановочны: lim lim * = lim lim *.
M >ro t ^ro M >ro t ^ro t ^ro M >ro
В основе доказательства теоремы б (а также ряда утверждений работ [81, 89, 90]) лежит следующий результат [92]: если последовательность марковских полугрупп слабо сходится к предельной полугруппе, то любая предельная точка из множества инвариантных мер для допредельных полугрупп является инвариантной мерой для предельной полугруппы.
Обратим внимание, что модель «хищник-жертва» в изложении и. 7.3 книги [22] является хорошим примером того, что может быть, если не выполняется условие устойчивости равновесия. В этой модели аттрактором (ДК) является цикл, которому соответствует инвариантная мера вида «кратера вулкана». Однако, как уже было ранее отмечено, lim и M -\ lim не перестановочны. Также хорошим примером к теореме 6 является модель Дж. А. t^ro
Томлина из раздела 2 с фиксированным числом web-страниц |К|. Даже в этом случае теорема б неприменима к модели Дж. А. Томлина, в которой в результате скейлинга появляются новые линейные законы сохранения. Соответствующая система (ДК) имеет инвариантным целое аффинное многообразие, чтобы определить, что будет происходить на этом многообразии, нужен более аккуратный анализ соответствующей инвариантной меры. Весьма похожая ситуация наблюдается и в BMW-модели равновесного распределения потоков из раздела 3, в случае, когда равновесие Нэша-Вардропа (по потокам на путях) не единственно. При этом здесь все происходящее еще отягощается необходимостью выбора достаточно малого параметра этой динамики Т > 0.
Результаты [17, 19, 20] и ряда других работ наталкивают на гипотезу: аттрактор динамической системы (ДК), который, как мы отмечали выше, может быть сколь угодно сложным множеством (например, в приложениях типичны случаи предельных циклов, нескольких положений равновесия и даже хаотических аттракторов), является таким множеством, в малой окрестности которого на больших временах с большой вероятностью будет пребы- вать рассматриваемая макросистема.
Причем тут возможны разные варианты поведения. Например, в случае двух притягивающих равновесий [20] динамика системы «притянется» к каждому из них с вероятностями, зависящими от точки старта, и далее система может пребывать в малой окрестности равновесия длительное время, до большой флуктуации (вероятность такой флуктуации может быть ничтожна мала на фиксированно конечном временном отрезке), которая сможет перебросить её в другое положение равновесия [93]. Другой тип поведения: постоянно циркулировать (перемешиваться) по аттрактору. Такая картина наблюдается, например, с «кратером вулкана» в модели «хищник-жертва». Возможен, конечно, и симбиоз отмеченных типов поведения.
Для доказательства ряда утверждений этой статьи полезным инструментом является аппарат производящих функций из статьи [94].
Работа выполнена при поддержке грантов РФФИ 10-01-00321-а, 10-07-00620-а, 11-01-00494-а, Лаборатории структурных методов анализа данных в предсказательном моделировании, ФУПМ МФТИ, грант правительства РФ дог. 11.G34.31.0073.
Список литературы О возможной динамике в модели ранжирования web-страниц PageRank и модернизированной модели расчета матрицы корреспонденций
- Jaynes E. T. Probability theory. The logic of science. -Cambridge: Cambridge University Press, 2003; Papers on probability, statistics and statistical physics. Dordrecht: Kluwer Academic Publisher, 1989.
- Вильсон А. Дж. Энтропийные методы моделирования сложных систем. -М.: Наука, 1978.
- Николис Г., Пригожин И. Самоорганизация в неравновесных системах. -М.: Мир, 1979.
- Хакен Г. Информация и самоорганизация. Макроскопический подход к сложным системам. -М.: УРСС, 2005.
- Шредингер Э. Статистическая термодинамика. -М.: ИЛ, 1948.
- Крылов Н. С.Работы по обоснованию статистической физики. -М.-Л.: Издательство АН СССР, 1950.
- Хинчин А. Я. Математические основания статистической механики. -М.-Ижевск: НИЦ «РХД», ИКИ, 2003.
- Кац М. Вероятность и смежные вопросы в физике. -М.: Мир, 1965.
- Хуанг К. Статистическая механика. -М.: Мир, 1966.
- Рюэль Д. Статистическая механика. Строгие результаты. -М.: Мир, 1971.
- Корнфельд И. П., Синай Я. Г., Фомин С. В. Эргодическая теория. -М.: Наука, 1980.
- Evans L. C. Entropy and partial differential equations. Department of mathematics, UC Berkeley, 2003. http://math.berkeley.edu/˜evans/
- Минлос Р. А. Введение в математическую статистическую физику. -М.: МЦНМО, 2002.
- Козлов В. В. Ансамбли Гиббса и неравновесная статистическая механика. -М.-Ижевск: НИЦ «РХД», ИКИ, 2008.
- Марри Дж. Нелинейные дифференциальные уравнения в биологии. -М.: Мир, 1983.
- Свирежев Ю. М. Нелинейные волны, диссипативные структуры и катастрофы в экологии. -М.: Наука, 1987.
- Гардинер К. В. Стохастические методы в естественных науках. -М.: Мир, 1986.
- Веденяпин В. В. Кинетическая уравнения Больцмана и Власова. -М.: Физматлит, 2001.
- Малышев В. А., Пирогов С. А. Обратимость и необратимость в стохастической химической кинетике//УМН. -2008. -Т. 63, № 1. -С. 3-36.
- Вайдлих В. Социодинамика: системный подход к математическому моделированию в социальных науках. -М.: УРСС, 2010.
- Castellano C., Fortunato S., Loreto V. Statistical physics of social behavior//Review of modern physics. -2009. -V. 81. -P. 591-646. arXiv:0710.3256v2
- Занг В. Б. Синергетическая экономика: время и перемены в нелинейной экономической теории. -М.: Мир, 1999. 23. Drˇ𝑎gulescu A., Yakovenko V. M. Statistical mechanics of money//The European Physical Journal. B. -2000. -V. 17. -P. 723-729. arXiv:cond-mat/0001432v4
- Baldi P., Frasconi P., Smyth P. Modeling the Internet and the Web: Probabilistic methods and algorithms. -Published by John Wiley & Sons, 2003.
- Розоноэр Л. И. Обмен и распределение ресурсов (обобщенный термодинамический подход) I, II, III//Автоматика и телемеханика. -1973, -№ 5, № 6, № 8.
- Горбань А. Н. Обход равновесия. -Новосибирск: Наука, 1984.
- Опойцев В. И. Нелинейная системостатика. -М.: Наука, 1986.
- Малишевский А. В. Качественные модели в теории сложных систем. -М.: Наука, 1998.
- Сергеев В. М. Пределы рациональности. -М.: Фазис, 1999.
- Попков Ю. С. Теория макросистем: равновесные модели. -М.: УРСС, 1999.
- Цирлин А. М. Методы оптимизации в необратимой термодинамике и микроэкономике. -М.: Физматлит, 2003.
- Швецов В. И. Математическое моделирование транспортных потоков//Автоматика и телемеханика. -2003. -№ 11. -С. 3-46.
- Маслов В. П. Квантовая экономика. -М.: Наука, 2006.
- Олемской А. И. Синергетика сложных систем: Феноменология и статистическая теория. -М.: КРАСАНД, 2009.
- Веретенников А. Ю. Параметрическое и непараметрическое оценивание для цепей Маркова. -М.: Изд-во ЦПИ при механико-математическом факультете МГУ, 2000.
- Боровков А. А. Эргодичность и устойчивость случайных процессов. -М.: УРСС, 1999.
- Булинский А. В., Ширяев А. Н. Теория случайных процессов. -М.: Физматлит; Лаборатория базовых знаний, 2003.
- Кельберт М. Я., Сухов Ю. М. Вероятность и статистика в примерах и задачах. -Т. 2. -М.: МЦНМО, 2010.
- Вишневский В. М. Теоретические основы проектирования компьютерных сетей. -М.: Техносфера, 2003.
- Ивницкий В. А. Теория сетей массового обслуживания. -М.: Физматлит, 2004.
- The maximum entropy formalism, ed. by R. D. Levin, M. Tribus//Conf. Mass. Inst. Tech., Cambridge, 1978. MIT Press, 1979.
- International workshops on Bayesian inference and maximum entropy methods in science and engineering. AIP Conf. Proceedings (holds every year from 1980).
- Kapur J. N. Maximum -entropy models in science and engineering. -John Wiley & Sons, Inc., 1989.
- Golan A., Judge G., Miller D. Maximum entropy econometrics: Robust estimation with limited data. Chichester, Wiley, 1996.
- Fang S.-C., Rajasekera J. R., Tsao H.-S. J. Entropy optimization and mathematical programming. -Kluwer's International Series, 1997.
- Маслов В. П., Черный А. С. О минимизации и максимизации энтропии в различных дисциплинах//ТВП. -2003. -Т. 48, № 3. -С. 466-486.
- Гасников А. В., Кленов С. Л., Нурминский Е. А., Холодов Я. А., Шамрай Н. Б. Введение в математическое моделирование транспортных потоков/под ред. А.В. Гасникова с приложениями М.Л. Бланка, Е.В. Гасниковой, А.А. Замятина и В.А. Малышева, А.В. Колесникова, Ю.Е. Нестерова и С.В. Шпирко, А.М. Райгородского. -М.: МЦНМО, 2012. http://zoneos.com/traffic/
- Гасников А. В., Гасникова Е. В. О возможной динамике в модели расчета матрицы корреспонденций (А. Дж. Вильсона)//Труды МФТИ (специальный выпуск, посвященный математическому моделированию транспортных потоков, под ред. акад. В.В. Козлова). -2010. -Т. 2, № 4(8). -С. 45-54.
- Brin S., Page L. The anatomy of a large-scale hypertextual web search engine//Comput. Network ISDN Syst. -1998. -V. 30(1-7). -P. 107-117.
- Langville A. N., Meyer C. D. Google's PageRank and Beyond: The Science of Search Engine Rankings. -Princeton University Press, 2006.
- Назин А. В., Поляк Б. Т. Рандомизированный алгоритм нахождения собственного вектора стохастической матрицы с применением к задаче PageRank//Автоматика и телемеханика. -2011. № 2, -C. 131-141.
- Nesterov Y. E. Subgradient methods for huge-scale optimization problems//CORE Discussion Paper 2012/2, 2012. http://www.uclouvain.be/32349.html
- Tomlin J. A. A new paradigm for ranking pages on the World Wide Web//Proceedings of the WWW2003, CityplaceBudapest, countryregionHungary, pages ACM 1-58113-680-3/03/0005, May 20-24, 2003. http://www2003.org/cdrom/papers/refereed/p042/paper42_html/p42-tomlin.htm; http://www.stanford.edu/group/SOL/software/pdco.html
- Шананин А. А. Математические модели в экономике//Годовой курс лекций для студентов ФУПМ МФТИ, ВМиК МГУ и РУДН http://dame.mipt.ru/video/matmodeli/
- Гасникова Е. В. Двойственные мультипликативные алгоритмы для задач энтропийно-линейного программирования//ЖВМ и МФ. -2009. -Т. 49, № 3. -С. 453-464.
- Кнут Д., Яо Э. Сложность моделирования неравномерных распределений//Кибернетический сборник. Новая серия. Вып. 19. -М.: Мир, 1983. -С. 97-158.
- Ермольев Ю. М. Методы стохастического программирования. -М.: Наука, 1976.
- http://www2.isye.gatech.edu/˜nemirovs/
- http://www.core.ucl.ac.be/˜nesterov/
- Гасникова Е. В. Исследование задач энтропийного программирования: диссертация на соискание звания магистра по специальности 05.13.18. ФУПМ МФТИ, ИСА РАН, 16 июня 2009.
- Stouffer S. A. Intervening opportunities: a theory relating mobility and distance//Amer. Sociolog. Rev. -1940. -V. 5. -P. 845-867.
- Fotheringham A. S. A new set of special-interaction models: the theory of competing destinations//Envir. & Plan. A. -1983. -V. 15. -P. 15-36.
- Fotheringham A. S. Modelling hierarchical destination choice//Envir. & Plan. A. -1986. -V. 18. -P. 401-418.
- Gon.calves M. B., Ulyssea-Neto I. Equilibrium values and dynamics of attractiveness terms in production-constrained spatial-interaction models//Envir. & Plan. -A. 1993. -V. 25. -P. 817-826.
- Стенбринк П. А. Оптимизация транспортных сетей. -М.: Транспорт, 1981.
- Patriksson M. The traffic assignment problem. Models and methods. -Utrecht, Netherlands: VSP, 1994.
- Sheffi Y. Urban transportation networks: Equilibrium analysis with mathematical programming methods. -N.J.: Prentice-Hall Inc., Englewood Cliffs, 1985.
- Bar-Gera H. Origin-based algorithms for transportation network modeling//Report. Univ. of Illinois at Chicago, 1999.
- Швецов В. И. Проблемы моделирования передвижений в транспортных сетях//Труды МФТИ (специальный выпуск, посвященный математическому моделированию транспортных потоков, под ред. акад. В.В. Козлова). -2010. -Т. 2. № 4(8). -С. 169-179.
- Foster D., Young P. Stochastic evolutionary game dynamics//Theoretical population biology. -1990. -V. 38, N 2.
- Cressman R. Evolutionary game theory and extensive form games. -Cambridge, Mass.: MIT Press, 2003.
- Hofbauer J., Sigmund K. Evolutionary game dynamics//Bulletin of the AMS. -2003. -V. 40, N 4. -P. 479-519.
- McKelvey R. D., Palfrey T. R. Quantal response equilibria for extensive form games//Experimental economics. -1998. -V. 1. -P. 9-41.
- Fogel D. B. Evolutionary Computation: Towards a New Philosophy of Machine Intelligence. -New York: IEEE Press, 2000.
- Хачиян Л.Г. Избранные труды/сост. С. П. Тарасов. -М.: МЦНМО, 2009. -С. 38-48.
- Como G., Salva K., Acemoglu D., Dahleh M.A., Frazzoli E. Stability analysis of transportation networks with multiscale driver decisions//e-print arXiv:1101.2220v1, 2011.
- Gasnikova E. V., Nagapetyan T. A. About new dynamical interpretations of entropic model of correspondence matrix calculation and Nash-Wardrop's equilibrium in Beckmann's traffic flow distribution model//Ninth International Conference on Traffic and Granular Flow, 28 September -1 October 2011. -Moscow: Springer, 2012. arXiv:1112.1628v3
- Juditsky A., Lan G., Nemirovski A., Shapiro A. Stochastic approximation approach to stochastic programming//SIAM Journal on Optimization. -2009. -V. 19, N 4. -P. 1574-1609.
- Nesterov Y., de Palma A. Static equilibrium in congested transportation networks//Networks Spatial Econ. -2003. -N 3(3). -P. 371-395.
- Разжевайкин В. Н. Эволюционная оптимальность и построение функционалов отбора в моделях структурированных биосистем//Труды VI Всероссийской научной конференции «Математическое моделирование развивающейся экономики и экологии» (ЭКОМОД-2011), Киров, 27 июня -3 июля 2011. -Киров: Изд-во ВятГУ, 2011. -С. 309-316.
- Malyshev V. A., Pirogov S. A., Rubco A. N. Random walks and chemical networks//Mosc. Math. J. -2004. -V. 4, N 2. -P. 441-453.
- Батищева Я. Г., Веденяпин В. В. II закон термодинамики для химической кинетики//Мат. мод. -2005. -Т. 17, № 8. -С. 106-110.
- Веденяпин В. В., Орлов Ю. Н. О законах сохранения для полиномиальных гамильтонианов и для дискретных моделей уравнения Больцмана//ТМФ. -1999. -Т. 121, № 2. -С. 307-315.
- Montenegro R., Tetali P. Mathematical aspects of mixing times in Markov chains. 2006. http://people.math.gatech.edu/˜tetali/PUBLIS/survey.pdf
- Diaconis P. The Markov chain Monte Carlo revolution//Bulletin (New Series) of the AMS. -2009. -V. 49, N 2. -P. 179-205.
- Joulin A., Ollivier Y. Curvature, concentration and error estimates for Markov chain Monte Carlo//Ann. Prob. -2010. -V. 38, N 6. -P. 2418-2442. http://www.yann-ollivier.org/rech/publs/surveycurvmarkov.pdf
- Sinclair A., Jerrum M. Approximate counting, uniform generation and rapidly mixing Markov chains//Information and Computation. -1989. -V. 82, N 1. -P. 93-133.
- Dyer M., Frieze A., Kannan R. A random polynomial-time algorithm for approximating of the volume of convex bodies//Journal of ACM. -1991. -V. 38, N 1. -P. 1-17.
- Rybko A., Shlosman S. Poisson hypothesis for information networks I, II//e-prints http://arxiv.org/abs/math/0406110v1; http://arxiv.org/abs/math-ph/0410053v1, 2004.
- Рыбко А. Н. Пуассоновская гипотеза для больших симметричных коммуникационных сетей//Глобус. Общематематический семинар/под ред. М. А. Цфасмана и В. В. Прасолова. № 4. -М.: МЦНМО, 2009. -С. 105-126.
- Богданов К. Ю. Прогулки с физикой. Библиотечка «Квант» В. 98. -М.: Бюро Квантум, 2006. Глава 18.
- Лигетт Т. Марковские процессы с локальным взаимодействием. -М.: Мир, 1989.
- Вентцель А. Д., Фрейдлин М. И. Флуктуации в динамических системах под действием малых случайных возмущений. -М.: Наука, 1979.
- Калинкин А. В. Марковские ветвящиеся процессы с взаимодействием//УМН. -2002. -Т. 57:2(344). -С. 23-84.


