О возможности формального объединения дескриптивных и прескриптивных высказываний в структуре научной теории

Упомянутая в названии статьи проблема была поставлена в ходе исследований структуры теоретического знания, предпринятых автором в 2009–2012 гг. [16]. Сама возможность проблематизации подобного объединения может вызвать сомнение, поскольку, несмотря на почтенную, почти трехсотлетнюю историю попыток вывести ценностные высказывания из истинностных, все они рано или поздно заслуженно критиковались и, в конце концов, предлагаемые различные схемы логического вывода всегда оказывались ошибочными. Один из самых известных примеров подобного рода критики представил еще Д. Юм*, в связи с чем одноименный принцип запрета (принцип Юма) впоследствии был отождествлен со зловещим и бескомпромиссным образом гильотины, обрубающей всякие надежды на положительное решение обозначенной проблемы в будущем.

Тем не менее, ценностные высказывания нередки в научных теориях, даже в тех из них, которые принято относить к так называемым точным наукам, не говоря уже о теориях описательного естествознания и социально-гуманитарных наук. Зачастую подобные высказывания не несут эвристического содержания, но иной раз их присутствие оказывается принципиальным для истинности теории и в любом случае дескриптивные и прескриптивные** высказывания образуют органическое единство, важное для правильного понимания контекста, который составляют образующие теорию утверждения. Тем не менее, за десятилетия исследований в области логической структуры теоретического знания так и не было выработано адекватных средств экспликации его нормативного содержания. При этом речь идет даже не о ценностях «в духе Лотце», подлежащих, если следовать классикам позитивизма, безусловной элиминации из структуры теории, а о вполне формализуемых оценках вроде «хорошо», «плохо», «лучше», «хуже» и прочих, для которых давно разработаны формальные исчисления высказываний [8; 10]. Отчасти это является следствием существования упоминаемого выше принципа, поскольку оценки не могут быть выведены из утверждений, содержанием которых является «истина» либо «ложь». Поэтому, несмотря на всю важность оценок для самой теории, ни их статус, ни их генезис в ее структуре не являются до конца проясненными. Помня об этом, мы, тем не менее, считаем возможным довольно органично «вписать» оценки (а, следовательно, ценности и нормы) в структуру теоретического знания. Основная идея развиваемого нами в настоящей работе подхода состоит в рассмотрении дескриптивных и прескриптивных утверждений как дополнительных по отношению друг к другу.

Использование понятия «дополнительности», пришедшего в философский лексикон из квантовой физики, требует для своего осмысления в первую очередь расширения ряда важнейших логических понятий, в частности (и в первую очередь), понятия противоречия. Исследования в области логической структуры квантовой механики, проведенные за последнюю четверть века [5; 14], убедительно показали, что, несмотря на скептическое отношение к данной проблеме ряда видных ее основоположников [3, с. 531], адекватное логическое описание феномена дополнительности нуждается в расширении множества значений высказываний посредством введения третьего логического значения – неопределенности.

В пользу отказа от двузначности можно выдвинуть два аргумента. Во-первых, как показывал в своих работах еще Г. Рейхенбах, а позднее, например, известный логик В.С. Меськов, адекватная логическая экспликация феномена дополнительности требует введения третьего истинностного значения – «неопределенно». Без этого шага невозможно непротиворечиво истолковать результаты квантовомеханических экспериментов [2, с. 75; 15]. Во-вторых, логика оценок (и в особенности, логика «абсолютных оценок») изначально строилась таким образом, чтобы множество значений оценочных высказываний наряду с «хорошо» и «плохо» включало также и оценку «безразлично» [10, с. 52]. Оговоримся сразу: наш собственный подход к экспликации логической структуры теоретического знания в ряде аспектов существенно отличается как от логических систем Лукасевича и Рейхенбаха, так и от логики оценок, описанной Ивиным, хотя и сохраняет преемственные черты по отношению к каждой из них.

Прежде всего, отличия касаются интерпретации третьего возможного значения истинности высказывания – «неопределенно». Как известно, и у Я. Лукасевича, и у Г. Рейхенбаха множество значений истинности произвольного высказывания является полностью упорядоченным. Это означает, что семантически значение «неопределенно» не является чем-то качественно иного рода, нежели «истинно» или «ложно» [4; 14, с. 39]. Согласно Рейхенбаху, отношение порядка, задаваемое на множестве значений высказываний, можно записать следующим образом: Л ≤ Н ≤ И [14, с. 37]. У Я. Лукасеви-ча значениям Л, Н, И соответствуют числа 0, ¹ , 1. Значение «неопределенно» (Н) вводится следующим образом:                            ²

• 1 .⌐ Н = Н;

• 2 . К стандартной таблице истинности импликации [1, с. 36]

p q p→q И И И И Л Л Л И И Л Л И добавляются пять новых строк [4]:

И	Н	Н
Н	Л	Н
Л	Н	И
Н	Н	И
Н	И	И

Как справедливо замечает В.С. Меськов, в результате полного упорядочения множества допустимых истинностных значений «неопределенно» предстает как равноположное со значениями «истинно» и «ложно»: все элементы множества истинностей данной системы являются сравнимыми один с другим. Однако такая интерпретация неопределенности совершенно не отвечает смыслу, вкладываемому в нее квантовой механикой, поскольку третье возможное значение истинности высказывания в этой ситуации делает значение самого высказывания вполне определенным.

Здесь следует заметить, что квантовомеханическая неопределенность отнюдь не соответствует ситуации, когда заданы два некоторых значения, а собственно неопределенность состоит в необходимости случайного выбора одного из них. В квантовой механике принимается, что состояние не существует до измерения. Поэтому когда говорят, что значение той или иной физической величины неопределенно, то подразумевается совсем не то, что она имеет в точности некоторое значение, случайно выбираемое из нескольких потенциально данных альтернатив. В этом случае неопределенность заключалась бы только в незнании, какая же именно из данных альтернатив нашла свое воплощение в реальности, но состояние до измерения вполне бы существовало. Несуществованию состояния до измерения (неопределенности) соответствует отсутствие (полное незнание) значений тех величин, которые образуют данное состояние. Мы считаем целесообразным в наших дальнейших рассуждениях сохранить этот важный нюанс для того, чтобы впоследствии положить его в основу развиваемой нами логической модели. На основании сказанного можно заключить, что значение высказывания «неопределенно» не может быть равнозначно с «истинно» и «ложно», а все множество значений в целом не может являться полностью упорядоченным. Мы полагаем, что неопределенное значение означает принципиальное отсутствие возможности констатировать истинность или ложность высказывания. В этом отношении наша система в чем-то соответствует системе ЛН, построенной В.С. Меськовым [14, с. 40–48].

Следует обратить внимание на то, что в логике абсолютных оценок безразличное значение ценностного высказывания также неравноположно с оценками «хорошо» и «плохо». Согласно мнению одного из создателей логики абсолютных оценок Э. Гуссерля, значение «безразлично» указывает на то, что высказывание не является оценочным [10, с. 56]. Таким образом, множество значений ценностных высказываний также не является полностью упорядоченным и, следовательно, оценочная логика фундаментально отличается от классической логики, содержащей, в частности, среди прочих и закон «исключенного третьего». Тем не менее, А.А. Ивин в своем изложении принципов логики абсолютных оценок подчеркивает, что она основана на классической пропозициональной логике [10, с. 52]. Этому, казалось бы, отвечает введение Э. Гуссерлем законов Va _л NVa («Всякий предмет или имеет ценность, или не обладает ею») и ~ (Va _л NVa) («Неверно, что предмет одновременно и является ценностью, и не является ею»)*. И все же мы склонны утверждать, что логика абсолютных оценок в силу отличия структуры множества значений высказываний не является классической двузначной логикой. На это указывает, прежде всего, то обстоятельство, что построение аксиологических аналогов законов исключенного третьего и противоречия требует одновременного использования двух типов отрицания: отрицания суждения, обозначаемого символом «~», и отрицания «общего имени» (отрицания «быть ценностью»), обозначаемого символом « N ». Невыполнение этого условия немедленно разрушает иллюзию двузначности добавлением третьей альтернативы: элиминация « N -отрицания» с заменой его «~-отрицанием» к значениям высказываний «хорошо» или «плохо» добавляет альтернативу «безразлично», а элиминация «~-отрицания» с заменой его « N -отрицанием» к именам «положительная ценность» и «отрицательная ценность» добавит также альтернативу «не быть ценностью». Нетрудно проверить, что такие элиминации отрицаний обессмысливают приведенные законы. Поэтому можно заключить, что каждый из рассмотренных типов отрицания отрицает на самом деле не одну, а две альтернативы, что для классической логики чересчур много.

Трактовка неопределенного и безразличного значений как неравноположных с соответствующими истинностными и ценностными значениями может осуществляться разными способами. Выше мы упоминали, что у В.С. Меськова имеется экспликация логической структуры квантовой механики, в которой неопределенное значение отождествляется с оценкой знания об истинности высказывания (система «ЛН» в терминологии автора). Неопределенность как мера незнания истинности высказывания о состоянии некоторой системы, как нетрудно заметить, плохо согласуется с утверждением о несуществовании данного состояния до измерения. Однако у этого же автора имеется и другой подход, использующий восходящее к Г. Лейбницу разделение истин на «истины логики» и «истины факта»

(система «ЛС») [14, с. 48–58]. В этой системе неопределенное значение означает «фактически неопределенно» и служит для описания в терминах логики специфического отношения между одновременно ненаблюдаемыми величинами. Согласно определению, данному В.С. Меськовым, предложение, обозначаемое как фактически неопределенное, соответствует некоторому фиксированному, но неизвестному положению дел в мире, и при установлении этого обращаются к содержанию предложения или к смыслу входящих в него дескриптивных терминов [10, с. 49]. При всех, на первый взгляд, значительных отличиях от системы «ЛН» следует, однако, признать, что утверждение о фиксированности фактически неизвестного положения вещей подразумевает его существование a priori . В данном пункте логическая система «ЛС» по сути представляет то же самое, что и система «ЛН»: в них обеих неявно подразумевается противоречащее принципам квантовой механики существование состояния до измерения, поскольку в них прямо или косвенно ставится вопрос о степени истинности некоторого априорного суждения об этом состоянии.

Теперь, учитывая сделанные замечания, мы можем выдвинуть собственную интерпретацию «неопределенности» и «безразличности», которая отражает факт неполной упорядоченности множеств {«истинно», «ложно», «неопределенно»} и {«хорошо», «плохо», «безразлично»}*. Главная ее идея: неопределенные и безразличные высказывания имеют природу, качественно отличную от, соответственно, истинных и ложных, хороших и плохих. Мы предлагаем считать неопределенное высказывание оценочным, могущим принимать значения «хорошо» или «плохо», а безразличное высказывание – описательным, принимающим значения «истинно» или «ложно». По нашему мнению, только таким образом можно удовлетворить требованию фактической невозможности получить достоверное знание о денотате a priori . В этом случае может идти речь лишь об оценке нашего знания (или незнания), которая может быть, соответственно, хорошей или плохой. Данная интерпретация неопределенности симметрична относительно двойственности: оценка перестает быть оценкой a posteriori , когда вероятностное знание становится достоверным, а неопределенное высказывание — истинным, либо ложным. Достоверное знание ценностно-нейтрально, поэтому описательное суждение должно быть охарактеризовано как оценочно-безразличное. Безусловно, такая, сильно упрощенная модель когнитивной деятельности, не может претендовать на полноту отражения процессов познания, но уже в таком прими-тивизированном виде она отражает их существенные черты и, что немаловажно, позволяет получить ряд нетривиальных следствий.

Важнейшим из таких следствий, на наш взгляд, является то обстоятельство, что такой подход к построению высказывания позволяет если не обойти совсем, то, по крайней мере, существенно ослабить принцип Юма, утверждающий невозможность перехода от описательных суждений к оценочным при помощи чисто логических средств [9, с. 267; 12]. То, что такой переход возможен, следует из равноправия и двойственности описательного и оценочного содержания выказывания. Более того, невозможно указать ни одного примера высказывания, содержащего формулировку закона природы либо общественного закона, в которой бы подобная двойственность нарушалась. Всякий раз, описывая сущее, мы тем самым формируем некий нормативный контекст, в рамках которого происходит дальнейшее постижение действительности. Указанный контекст образуют не только общепринятые в науке методологические нормы, но и вновь открываемые законы, точнее требование согласования с ними впоследствии получаемого знания. Проще говоря, каждый закон, помимо «описания сущего», наравне с ним включает также «требования должного»: оценки и нормы, с которыми сопоставляется получаемое впоследствии знание.

Мы утверждаем, что оценка получаемого нового знания предшествует его логическому анализу. Отталкиваясь от некоторой теории и получая результат, находящийся в прямом противоречии с ее при нципами, можно быть уверенным в ошибочном результате, даже если самой ошибки не заметно на первый взгляд. Например, если в процессе построения физической теории будет получен результат, находящийся в противоречии с законом сохранения энергии, то ученые обязательно начнут искать ошибку в постулатах или рассуждениях вне зависимости от того, кажутся они убедительными или нет. Именно поэтому мы и говорим о норме и о нормативном характере теоретического закона, поскольку в описанном примере и многочисленных ему подобных связь между обнаружением противоречия и поиском ошибки носит характер долженствования. При этом совершенно неважно, существовало ли противоречие на самом деле или было кажущимся – главное то, что осознание противоречия вызывает определенный сценарий поведения, а также то, что мотивы для инициирования данного сценария могут быть не осознаваемы явно.

Сочетание в одном объекте сущностных и оценочно-нормативных компонентов характерно не только для теоретических законов. Гораздо более важно, что такая же двойственная структура характерна и для теоретических объектов. Поскольку они всегда строятся путем идеализации реально существующих прототипов (такие, например, как материальная точка) или конструируются на их основе (как квантовомеханическая «волна-частица»), то наряду с описательной, их структура также необходимо включает и оценочно-нормативную часть, устанавливающую критерии соответствия заранее определенным условиям. Иными словами, как и в теоретическом законе, в абстрактном теоретическом объекте наличествует сложная связь между его формально-логической и ценностно-нормативной организацией. Необходимость последней можно проиллюстрировать тем фактом, что любой абстрактный объект, будучи образован в ходе формальных процедур, самим своим существованием предписывает исследователям определенный сценарий последующих действий, основным мотивом которых является не что иное, как продиктованное свойствами абстрактного объекта долженствование. Например, появление на авансцене физики в начале ХХ века «корпускулярно-волновых кентавров» мотивировало ученых практически с нуля создать не только новую теорию, но целый новый физический язык, в котором наряду с появлением принципиально новых средств, старые языковые средства приобрели совершенно новый смысл. Сохраняя ряд общих с прочими теориями естествознания черт, квантовая механика принципиально отличается от своих предшественниц. В этом случае принято говорить, что теория имеет «внутреннюю логику» развития, которая предписывает ученым куда и как двигаться. Но эта «внутренняя логика» не может иметь логическую природу – принцип Юма резко разграничивает области этического и логического. Поэтому, следует либо отказаться от данного принципа применительно к описанию динамики теоретического знания и считать, что логическое способно детерминировать этическое пусть даже и в таком узком аспекте, как построение частной теории, либо признать существование в структуре теоретических объектов ценностного начала, обладающего не меньшей важностью и значимостью, нежели формально-логическое. Но в любом случае «принцип Юма» должен быть смягчен, поскольку существование и развитие системы теоретического знания – наглядная иллюстрация взаимодополнительности и взаимообусловленности сущностного и нормативного начал – истины и ценностей, которые лишь во взаимодействии обеспечивают эвристический потенциал теории. При этом ее ценностно-нормативная структура играет роль «обратной связи» от исследуемого объекта к самому исследователю, олицетворяя ту самую «внутреннюю логику» развития теории, о которой мы писали выше. Будучи взятыми по отдельности, ни формальная структура, ни ценности не способны объяснить особенностей генезиса теоретического знания. Редукция теории к цепочке утверждений, связанных между собой отношением выводимости, как показывает в целом неудачный опыт неопозитивистской программы, не позволяет адекватно объяснить необходимость смены теорий. Взятая обособленно ценностная сфера теории лишает последнюю строгости и, в конечном итоге, практической значимости, лишь подчеркивая обоснованность мнения о необходимости элиминации ценностей. Поэтому необходимо признать значимость именно взаимодействия номологических и аксиологических структур теоретического знания, в конечном итоге замыкающихся на активном сознании исследователя – главном компоненте структуры теоретического знания.

Теперь, основываясь на сделанных замечаниях, мы можем приступить к изложению основных логических принципов нашей концепции «истинностно-ценностной дополнительности». Для начала необходимо определить адекватную интерпретацию для символических переменных p и q, отождествляемых с высказываниями . Прежде чем начинать поиски в данном направлении, придется учесть, что невозможно прямое соотнесение описательных и ценностных суждений, как различающихся множествами определений и значений. Поэтому, чтобы устранить данное препятствие, придется вводить различные содержательные интерпретации для переменных, выходящие за рамки собственно логики. Пример одной из таких интерпретаций мы изложим ниже.

Условимся считать p и q – суждениями, способными принимать значения на множестве: «истинно» (И), «ложно» (Л), «неопределенно» (Н) (описательные суждения) и на множестве: «хорошо» (Х), «плохо» (П), «безразлично» (Б) (абсолютные оценочные суждения) [10, с. 52]. Установим соответствие следующего вида:

• 1.    Н ↔ ( Х, П ) (Н эквивалентно Х или П);

• 2.    Б ↔ ( И, Л ) (Б эквивалентно И или Л).

То есть, когда описательные суждение определяется на множестве оценок, это соответствует неопределенности. Аналогично, задание оценочного суждения на множестве истинностных значений соответствует безразличной оценке. Таким образом, мы добились устранения главного препятствия – p и q задаются и принимают значения теперь на одном и том же множестве.

Следующий шаг – обобщение операции дополнительности ∆ на оценочные суждения. Зададим двойственную к ∆ операцию оценочной дополнительности ∇ при помощи следующей таблицы:

p	q	p ∇ q
Х	Х	П
Х	Б	Х
Х	П	П
Б	Х	Х
Б	Б	Х
Б	П	Х
П	Х	П
П	Б	Х
П	П	П

Мы видим, что данная операция строится полностью аналогично операции Δ. Двойственность их заключается в том, что когда p ∆ q принимает значения (И, Л), p ∇ q принимает значения (Х, П) соответственно.

Одновременное сосуществование указанных операций схематично отражает основные особенности структуры мышления субъекта, которое сочетает как содержательную, связанную с экспликацией вида причинно-следственных закономерностей, сторону, так и сторону деятельную, устанавливающую конкретный алгоритм этой самой экспликации. Существует изначально принципиальная неопределенность в природе высказываний p и q, которые могут быть как описательными, так и оценочными. Реальные суждения, используемые при построениях теорий, очень редко целиком принадлежат к какому-либо одному из указанных классов. Полная формализация очевидным образом исключает нормы и оценки из структуры теории (теоретических законов) и вместе с ними условия, при которых устанавливалась истинность или ложность гипотез. Другая же крайняя ситуация, обратная предыдущей, превращает теорию в «практическое руководство» познавательной деятельностью, в рецепт, который описывает последовательность шагов, но ничего не способен объяснить, поскольку не содержит эксплицированных закономерностей, выражаемых в терминах истины и лжи. В любом из этих случаев информативность теории невосполнимо уменьшается.

В качестве примера оценок можно привести часто встречающиеся в научной литературе речевые обороты наподобие «очевидно, что…», «легко показать, что…», а также «трудно», «элементарно» и т.п. Так же, как уже отмечалось нами в сноске выше, качественно схожую роль в изложении теорий играют и нормы «необходимо», «достаточно», «должно», «надлежит» и подобные им. В приведенной ниже цитате классика естествознания видно, как переплетаются друг с другом ее дескриптивное и прескриптивное содержание (выделенные нами различным образом): «… пр итя г ат ел ь н ая с ил а всего тела происходит и слагается из притягательных сил его частиц, и когда увеличивается количество вещества, то в той же пропорции надлежит увеличивать или уменьшать и его притягательную способность . … действие Земли должно рассматривать как состоящее из действий отдельных частиц ее , следовательно и в с е з е м н ы е т ел а в з аи м -но притягиваются с абсолютными силами, пропорциональными массе пр итя ги в аю щ е го т ел а» [13, с. 7]. Опираясь на этот и подобные ему примеры, можно уверенно утверждать, что оценочное и нормативное содержание не просто усиливает впечатление от текста, но передает читателю уникальную, несводимую к дескриптивной информацию, имеющую эвристическое значение в рамках рассматриваемой теории.

Теперь осталось рассмотреть формально-логическую сторону вопроса. Согласно принятому в логике подходу, необходимо установить корректность, непротиворечивость и полноту соответствующего трехзначного исчисления высказываний, содержащего находящиеся в отношении дополнительности истинностные и оценочные значения. Предваряя дальнейший анализ, заметим, что в силу полной симметрии данного исчисления относительно описательной и оценочной составляющих, его допустимо рассматривать как трехзначное с учетом сделанных нами выше замечаний. Поэтому в нем не будет справедлив закон исключенного третьего p v — p , а также закон противоречия — ( p л — p ) .

Опираясь на сказанное, определим трехзначное исчисление высказываний (обозначим его ИВ3(6)) следующим образом:

Определение 1. Исчисление высказываний ИВ₃₍₆₎ имеет алфавит, включающий в себя:

Символы пропозициональных переменных p, q, r, … ;

Кванторы:

(всеобщность);

(существование);

Унарный оператор  (логическое отрицание);

Бинарные операторы:

→ (импликация);

(конъюнкция);

(дизъюнкция);

(дополнительность);

Вспомогательные символы — открывающая и закрывающая круглые скобки () .

Определение 2. Правилом вывода в ИВ₃₍₆₎ является правило modus ponens.

Анализ свойств ИВ3(6) начнем с проверки выполнимости аксиом стандартного, двузначного исчисления высказываний (ИВ). Эти аксиомы обычно записываются в следующем виде [6, с. 47]:

p ^ (q ^ p)                      А1

(p ^ (q ^ r)) ^ ((p ^ q) ^ ( p ^ r))                      А2

А3

A4

A₅ A 6 A₇ A₈ A₉

(p ^ q ) ^ ((p ^ -q ) ^ -p )                    А0

Аксиома А10 часто записывается в следующем виде [7, с. 24]:

(—p > — q ) ^ ((—p ^ q ) ^ p )                      "

Путем непосредственной проверки нетрудно убедиться, что из приведенных аксиом в ИВ3(6) выполняются все, кроме А10 и        . Последняя аксиома не всегда приводит к тавтологии, в ряде случа ев давая неопределенное значение. Примером такого случая может служить следующая цепочка импликаций и равенств:                                               . Это легко понять, если учесть, что аксиома А10 является следствием закона исключенного третьего: при условии его выполнения ее можно вывести из остальных аксиом [6, с. 54]. Оформим данное утверждение в виде теоремы.

Теорема 1. Аксиома А₁₀ выводима из аксиом А₁ — А₉ и закона исключенного третьего.

Доказательство. Запишем для удобства аксиому А₈ в виде

.

Положим:                          . Имеем:

(q -^ -.p) -^ ((-.q -^ -.p) -^ ((qV-iq) -^ -.p))

Применяя правило контрапозиции                       к обеим частям выражения, приво дим его к виду:

.

Теперь трижды применяя лемму «о дедукции»*, получаем:

.

Переставим местами гипотезы, выстроив их в следующем порядке:                             , а затем дважды применим лемму «о дедукции» в обратную сторону. Окончательно получим:

(qV-iq) h (p ^ q) —> ((p -^ -.q) -^ -np)

Теорема 1 доказана.

Замечание 1. В ИВ₃₍₆₎ справедливы все теоремы ИВ , при формулировке и доказательстве которых не используется закон «исключенного третьего» (в частности, лемма о дедукции).

К числу аксиом ИВ3(6) добавим еще несколько специфичных:

^p^q)^(r^s)^ (p^q^QrVs) (pVq)Ar

A 11

A12

A 13

Продолжим построение исчисления высказываний. Таблицы истинности для пропозициональных связок будут иметь вид (таблицы истинности для импликации, дополнительности и оценочной дополнительности были приведены выше):

А) Отрицание:

p	p
И Л Н Б) Дизъюнкция:	Л И Н
p	q
И	ИИ
И	НИ
И	ЛИ
Н	ИИ
Н	НН
Н	ЛН
Л	ИИ
Л	НН
Л В) Конъюнкция:	ЛЛ
p	q
И	ИИ
И	НН
И	ЛЛ
Н	ИН
Н	НН
Н	ЛЛ
Л	ИЛ
Л	НЛ
Л	ЛЛ

Теперь рассмотрим вопрос о корректности, полноте и непротиворечивости ИВ3(6).

Теорема 2 (корректность ИВ₃₍₆₎). Всякая теорема ИВ₃₍₆₎ — тавтология.

Доказательство. Путем непосредственной проверки несложно убедиться, что аксиомы А₁ — А₉ выполнимы в ИВ₃₍₆₎, т.е. являются тавтологиями. Корректность правила modus ponens , использующегося при выводе теорем ИВ₃₍₆₎, следует из свойств импликации: если импликация p→q и ее посылка p всегда истинны, то по определению импликации следствие q также всегда истинно. Таким образом, все формулы, входящие в выводы (все теоремы) являются тавтологиями.

Теорема 3 (полнота ИВ₃₍₆₎). Всякая тавтология — теорема ИВ₃₍₆₎.

Доказательство. Предположим обратное, т.е. что не всякая тавтология выводима из аксиом ИВ₃₍₆₎ по правилу modus ponens . Символически это запишется следующим образом:

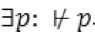
Это означает, что не существует последовательности формул, из которых каждая является либо аксиомой ИВ3(6), либо выводом из множества аксиом, последней в которой стоит формула p. Следовательно, в последовательности                    хотя бы одна промежуточная формула должна быть или ложной, или неопределенной.

Обозначим символом Г множество аксиом ИВ₃₍₆₎:        , и рассмотрим правило modus ponens :

Ay A^Vj

.

Из свойств импликации следует, что неопределенность или ложность формулы pi влечет за собой неопределенность или ложность всей импликации Ai → pi. Рассмотрим вывод формулы p из последней формулы в последовательности:                . Импликация является ложной или неопределенной лишь в трех случаях:

Посылка истинна, следствие ложно;

Посылка истинна, следствие неопределенно;

Посылка неопределенна, следствие ложно.

Рассмотрим все три случая. Первый случай не может быть выполнен, поскольку p – тавтология. Второй случай не выполняется по той же причине. Третий случай не выполняется, поскольку посылка – аксиома ИВ₃₍₆₎, а следствие – тавтология. Таким образом, импликация всегда истинна и, следовательно, произвольная тавтология выводима из последней формулы в цепочке:       .

Теперь последовательно применяя лемму «о дедукции» можно показать то же самое для n – 1-го члена последовательности (              ) и всех предыдущих. Окончательно будем иметь:

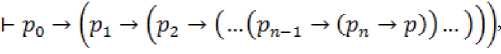
что означает, что произвольная тавтология выводима в ИВ3(6).

Таким образом, мы пришли к противоречию с первоначальным предположением:        , т.е.

не существует тавтологии, невыводимой в исчислении высказываний ИВ3(6). Теорема 3 доказана.

Прежде чем рассматривать вопрос о непротиворечивости ИВ3, введем следующее определение:

Определение 3. Некоторое множество формул Г называется совместным , если существует набор значений переменных, при которых все формулы из Г истинны.

В соответствии с данным определением, множество аксиом ИВ3(6) – совместно. Теперь можно приступить к доказательству теоремы о непротиворечивости исчисления высказываний ИВ3(6).

Теорема 4 (непротиворечивость ИВ₃₍₆₎). Исчисление высказываний ИВ₃₍₆₎ непротиворечиво.

Доказательство. Докажем теорему «от противного». Как известно, непротиворечивость исчисления высказываний означает, что из его аксиом нельзя вывести одновременно некоторую формулу и ее отрицание. Пусть множество аксиом ИВ₃₍₆₎ противоречиво. Так как оно совместно, то существуют значения переменных, при которых все формулы, выводимые из него истинны, в том числе p и p . По теореме 2 из множества аксиом ИВ₃₍₆₎ выводимы только тавтологии (т.е. только p ), поэтому допущение теоремы 4 о противоречивости множества аксиом противоречит теореме 2. Следовательно, сделанное выше допущение неверно, что и доказывает теорему 4.

Интересно, что невыполнимость закона «исключенного третьего» по сути ничего не меняет в доказательстве, поскольку приводящие к неопределенностям аксиомы исчисления высказываний исключены нами из числа аксиом ИВ₃₍₆₎, а импликация сохраняет истинность пропозициональных переменных. Логическое же отрицание истины дает ложь, как и в обычном исчислении высказываний. Поэтому, пользуясь правилом modus ponens , из аксиом неопределенное выражение получить нельзя.

Таким образом, мы имеем все основания для того, чтобы констатировать возможность существования «ядра» теоретического знания, построенного по принципу комплементарного соотношения между его основными составляющими. Нами показано, что такой подход отражает основные особенности мышления, соединяющего операции логического вывода и оценки в неразрывное целое.