О возможности формирования двумерных теневых радиоизображений нарушителей в охранных системах ближней радиолокации
Автор: Чернышев Максим Николаевич, Чернышев Николай Иванович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Электромагнитная совместимость и безопасность оборудования
Статья в выпуске: 1 т.10, 2012 года.
Бесплатный доступ
В статье рассмотрена методика формирования теневого радиоизображения путем восстановления функции пропускания нарушителя по его дифракционной картине для последующего определения части геометрических размеров и классификации нарушителя.
Охранные системы ближней радиолокации, интеграл френеля-кирхгофа, обратное преобразование, функция пропускания, теневой контур нарушителя, размер нарушителя
Короткий адрес: https://sciup.org/140191537
IDR: 140191537 | УДК: 621.396.96
Текст научной статьи О возможности формирования двумерных теневых радиоизображений нарушителей в охранных системах ближней радиолокации
Увеличение длины периметра охраняемой зоны при использовании радиолокационной технической системы охраны (РЛТСО) приводит к возрастанию затрат, связанных с идентификацией вида нарушителя. Использование аппаратуры, определяющей некоторые параметры нарушителя, например часть его геометрических размеров, позволит обеспечить распознание типа нарушителя и как следствие – снизить количество ложных тревог из-за объектов, не представляющих угрозы для охраняемой зоны. В работе рассмотрено возможное решение этой проблемы путем восстановления вида функции пропускания Р„р (х, у) трехмерного непрозрачного для электромагнитного (ЭМ) поля нарушителя по его дифракционной картине.
Восстановление вида одномерной функции пропускания нарушителя
На рис. 1 приведена схема пересечения охраняемой зоны РЛТСО [1] нарушителем, моделируемым в виде эллиптического цилиндра. Нарушитель перемещается в охраняемой зоне параллельно оси x, при этом координаты его центра и размеры по осям x, y и z равны соответственно Х0’ Уо’ RH и 2a; b и c. Векторы fиS проведены из точек P0 и P расположения передатчика (ПРД) и приемника (ПРМ) РЛТСО в произвольную точку поверхности Q нарушителя, через которую проходит и вектор нормали п. Для определения геометрических размеров нарушителя используем зависимость комплексной амплитуды ЭМ-поля U(P) в точке P от координаты X q . При определении U(P)
воспользуемся дифракционной формулой Френеля-Кирхгофа [2]:
Ai Гг/МХ’У)еХР[1к(Г +s)l и (Р) =--— ---------------X
22 у rs , (1)
х [cos( п, г) - со s(n, s)^dS где Г, S – модули векторов г и s ; к = 2л/X, X – длина волны ЭМ-поля; S – поверхность, по которой осуществляется интегрирование; dS – элемент площади этой поверхности.
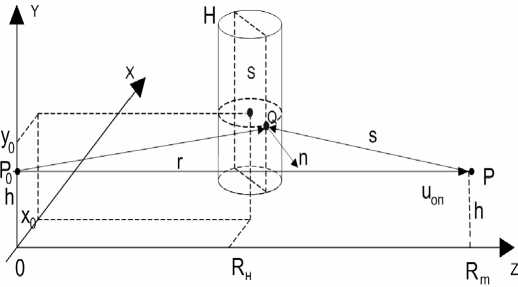
Рис. 1. Модель пересечения нарушителем охраняемой зоны
Разложение в выражении (1) r и s в ряд в окрестности ХО’ Уо с последующим отбрасыванием членов начиная с квадратичного приводит к дифракции Фраунгофера, а начиная с кубического – к дифракции Френеля [2]. Для этих типов дифракции восстановление функции пропускания возможно при использовании обратных преобразований Фурье и Френеля соответственно. Наряду с этим обратные преобразования Фурье и Френеля являются упрощениями некоторого более общего преобразования, так же как дифракционные интегралы Фраунгофера и Френеля являются частными случаями выражения (1). Для определения его одномерного вида используем случай дифракции ЭМ-волн на щели в плоском экране с шириной 2а по оси x от протяженного источника. Для него выражение (1) преобразуется к виду
Ai "rA„(x)exp[ik(r(x0) + s(x0))] U(P)---—------------------- x
22 r(x0Hx0)
x^-Rh ^dx, Ф^} s(x0)
O(x0) = w0V2 j/(x)exp[iw2(x0 -<^)2]^;
/(^) = w0V2 Jo(x0)exp[-iwo(^-x0)2]c/x0 ,
где r(x0) = УиТ^УТ^У;
S(xo) = 7(x + x0)2 +(Ди -^я)2 .
По аналогии с обратными преобразованиями Фурье и Френеля выражение, восстанавливающее вид изменения зависимости одномерной функции пропускания нарушителя, можно получить заменой в (2) P„p^ на U(P) и показателя степени в экспоненте на комплексно сопряженный, то есть
где /(^) – функция переменной ^’ а Ф(х0)– ее френелевский образ.
Обозначая в выражении (5) для U(P,x0)
k[— 2R
2(Rm-RH)
] = Wo2 И x = -^, в соот-
ветствии с первым из пары преобразований Френеля можно утверждать, что U(P,xfi) является
френелевским образом функции Pnp C^) при выполнении условий (4). Поэтому, в соответствии со вторым из пары преобразований Френеля можно
утверждать, что
P 2 22 г(х0Ж) (3)
r(x0) s(x0)
Действительно, представляя в (3) r(x0) и х(х0) в виде разложения в ряд по степеням
-----’получим: r(x0) « RH +
R»
(х + х0)2 2RH
s(x0)«Rm-RH +
(х + хо)2 2(Rm-RH)
Последние переходы возможны только при
выполнении условий
[£±25l]2 « ! [ x + x0 ] « ! 2Rh z(Rm-RH)
Подставляя полученные упрощенные выражения для r(x0) и s(x0) в показатель экспоненты выражения (2) и считая их равными, соответственно, Rh и Rm RH в знаменателе подынтегральной функции, придем к следующему упрощенному виду зависимости комплексной амплитуды электромагнитного поля U(P,x0) от координаты x0 нарушителя:
U(P,x0)~k[— ZK x expiikl--H 2RH
1 R JK(X)X
2\Rm ~ kh) (5)
Жт-кн)
■)(x + х0)2]Дх.
Полученное выражение можно считать одномерным преобразованием Френеля функции Л/х)’ так как пара преобразований Френеля представляется в следующем виде[3]:
A, (X) - k[-L + 1 ] Ju(P, x,) X
1 1 2
x exp[-ik(-- 1-- )(x + x 0) "\dx 0 .
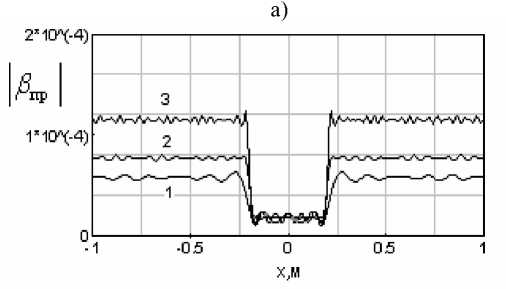
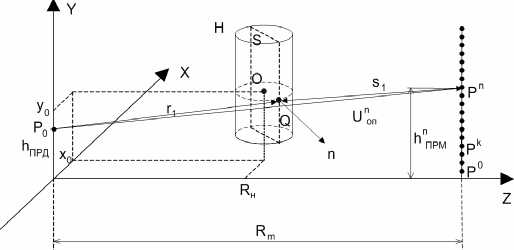
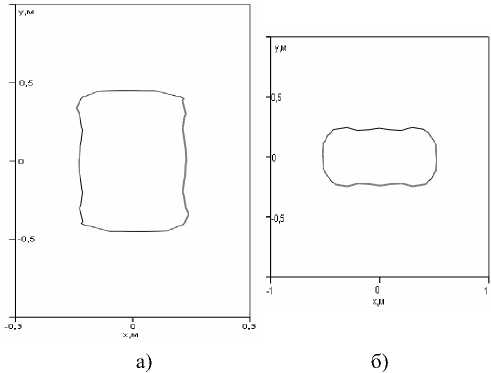
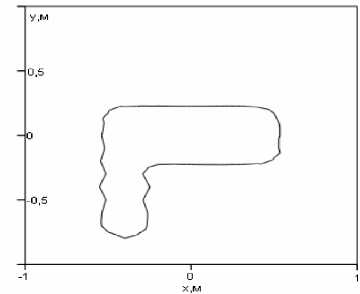
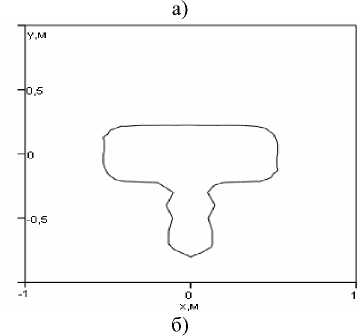
У V2RH 2 Выражения (5) и (6), ставящие в соответствие функции P np (^") ее френелевский образ U(P) и обратно, являются частным случаем (2) и (3) при условиях (4), поэтому можно сделать вывод, что эта пара преобразований аналогична паре преобразований Френеля, но являются более общей. Действительно, применение обоих преобразований (3) и (6) для восстановления Pnp (^) при выполнении условий (4) по значениям комплексной амплитуды электромагнитного поля U(P,x0), рассчитанного в соответствии с выражением (1), дает одинаковые результаты. При приближении нарушителя к антеннам ПРД или ПРМ на расстояния Rh илиRm-RH,нарушающие условия (4), прекращается восстановление Pnp (X) с помощью обратного преобразования Френеля (6), при восстановлении в тех же условиях с помощью преобразования (3). Это приводит к уменьшению размеров «мертвых» зон около антенн ПРД и ПРМ, в которых невозможно восстановление функции пропускания нарушителя, что является полезным эффектом данного преобразования ценой некоторого его усложнения. При дальнейшем уменьшении или Rm-RHи нарушении общего условия применимости дифракционной формулы Френеля-Кирхгофа прекращается и восстановление Pnp (^) с помощью преобразования (3) . При восстановлении вида функции пропускания путем расчета на ЭВМ вычисление интеграла заменялось вычислением суммы, а функция U(P,x0) непрерывного аргумента Xg – функцией дискретного аргумента Xgm • j 2M №~—£u(xoj 2л m=0 expl-ik^x + x^+T?; )] ------ ----x д/(х + ХОт)" +RH x ехрНк(д/(X + xOm)2 + (Rm -RHf)^ V(x + x0m)2+(T?„-^)2 xM^^OmM^Rjl V^^^mT^C^m Rh) где xOm= ^m-M>xti, Ax0 – шаг дискретизации координаты x0, IM – число отсчетов комплексной амплитуды. На рис. 2а приведены результаты расчета значений |U(P)| по выражению (1) при размерах двух полуосей эллипса (см. рис. 1) a =0,2 м ; c=0,3 м и половиной высоты цилиндра b=0,8 m, а на рис. 2б – результаты восстановления вида функции Pnp (X) в соответствии с выражением (3) приRm=150m; Я = 0,016м, A = IS для высоты размещения антенн ПРД и ПРМ h = Уо и равной 1 м. b и координаты У о его центра не приводят к заметному изменению определяемого размера 2а нарушителя, хотя при этом наблюдаются существенные изменения |U(P)|- Аналогичные результаты получены и при восстановлении вида функции пропускания по координате x щелей и прямоугольных отверстий в плоском экране. Условием восстановления функции пропускания двумерных и трехмерных объектов является использование определенной части дифракционной картины нарушителя, например отсчетов U(P) по сечению их двумерных дифракционных картин плоскостью, параллельной плоскости xoz и проходящей через линию РОР , при условии пересечения нарушителем этой линии. Приведенные результаты определения размера нарушителя в направлении его перемещения показывают работоспособность предложенного в работе подхода и позволяют использовать его и для определения одного из размеров двумерной и трехмерной модели нарушителя. Восстановление вида двумерной функции пропускания объекта При определении зависимости функции пропускания и геометрических размеров нарушителя по координате ¥ используем вертикальную линейку точечных приемных антенн для регистрации значений ЭМ-поля в точках Р с координатами 0, ^ПРМ и Rm по осям X, Y и Z соответственно как функции его координаты х0 неподвижными приемными элементами, находящимися в точках рп (см. рис. 3) [4]. Рис. 2. Результаты расчета значений |й(Р)| (рис. 2а) при RH = 75 м для кривой 1, R„= 125 м для кривой 2 и R„ = 140 м для кривой 3 и восстановления функции пропускания Д (х)(рис. 26) по U(P) , соответственно для кривых 1-3 рис. 2а В соответствии с рис. 2б размер нарушителя по направлению Х равен 2а = 0,4м. Отметим, что значительные изменения высоты цилиндра Рис. 3. Формирование сигналов в точках нахождения антенн ПРМ вертикальной линейки ПРМ РЛТСО Очевидно, что для двумерного случая векторы г, и S, будут определяться выражениями: р =(x + x0)i +(у-ЬПРД)) + RHk, s, = (х + x0)i + (у - hnPM ) j + (Sm - RH )k, (8) при этом вектор S1 индивидуален для каждого приемника и с учетом его высоты ^ПРМ должен быть переопределен как s" = (x + x0)i + (y-h;P,,)) + UL -RH)k. (9) Полученные в результате вычислений по формуле (1) значения комплексной амплитуды электромагнитного поля U(Pn) в точке нахождения каждого ПРМ будут являться функцией непрерывного аргумента X Q и дискретной переменной n- U(P") = U(x0,n). В предельном случае размещения на вертикальной линейке континуума ПРМ комплексная амплитуда преобразуется в функцию двух непрерывных аргументов Xq и ^прм U(P) - U(x 0, hnpM) . Поэтому преобразование, обеспечивающее восстановление двумерной функций пропускания, в общем случае должно основываться на двойном интеграле от двумерной комплексной амплитуды U(x (), hnPM ) и интегрирование должно производиться по переменным x0и hnpM . Возьмем за основу подынтегральной функции искомого двойного интеграла аналогичную функцию выражения (3) и отметим следующее. При перемещении нарушителя параллельно оси X изменяется координата его центра Xq (без изменений значений УоиRu), при этом входящие в (3) модули векторов f и s для случая двумерной дифракции изменяются в соответствии с выражениями (8), в которых вектор f, зависит только от переменной X„ ’ а вектор S, зависит от обеих - X0 И^ПРМ’ что также должно соблюдаться и в искомом обратном преобразовании. Производя замену векторов г и s, а также их модулей на h и s, и однократное интегрировании по xo на двукратное по xoиhnpM, получим искомое преобразование в виде: 2Л exP [—* к(Лх + x 0) + (у — ИПРд ) + RH )] X---- —---X ^) (x + x 0) + (у — ИПРД ) + RH exp[-ik^x + Xg)2 +(у-ИПРМУ +(Rm-RH^ )] X------ -------X \(^^о)~^(У~^Ъ1Рм)~^^п~^^^ (x+Xq) + (у —^Прд) ^^Н __________Rn -Rm____________Idx dh /---------1---------------;--------------- JUA о инпрм. (x + x0) + (y — hnPM) +(Rm-RH) Проверка возможности восстановления вида двумерной функции пропускания с помощью преобразования (10) затруднительна ввиду сложности задания двумерной комплексной амплитуды U(xo’^№jm) в аналитическом виде. Для проведения численных расчетов необходимо перейти к дискретным аргументам X От И^ПРМ ' Возвращаясь к реализуемому практически размещению антенн ПРМ в точках P" с координатами 0, ^ПРМИ Rm по осям X, Y и Z соответственно с заменой операций интегрирования на операции суммирования, получим: 1 IM 2N , А/Х,У)~ — EEU(XOm,hnPM)x exp[—ik(^/(x + x Om) + (у — ИПРд) + RH )] x-- =--x д)(х + хОт) +(y — Ипрд^ +RH x^PHk(j(x + x^7T(y^d7T(R7^ V(x + X0m)2 ^J-h^PM)2 +(^m у (x + x Om) + (у Ипрд) + RH ----------------------------------- ] Ax g Ah npM. V(x + xom) ЛУ ^прм^)+^m ^н) (H) В выражении (11) 2N обозначает число ПРМ на вертикальной линейке, ^hnPM – расстояние между n и (n + 1)-ым ПРМ. Для случая эквидистантного размещения ПРМ Ah nPM Ah npM и ^ прм ^ прм ft Ah pPM, h npM – координата по оси Y нижнего ПРМ, xom =(m-M)Z\x0, Ax0 – шаг дискретизации x0, 2M – максимальное значение индекса суммирования m, h*(XOm’hnPM) – отсчет двумерной комплексной амплитуды поля с выхода n-го ПРМ при значении координаты Xq центра нарушителя равной X()m . На рис. 4 приведены линии уровня (Л/Х,У) = const) результатов восстановления двумерной функции пропускания объектов, моделируемого различным образом ориентированными эллиптическими цилиндрами, при проходе нарушителя «в рост» (рис. 4а) и в положении «согнувшись» (рис. 4б), при учете только горизонтальной части тела нарушителя. Ширина нарушителя, отсчитанная по рис. 4а, составляет 0,4 м; высота – 0,8...0,9 м. Полученные размеры хорошо совпадают с параметрами размера модели нарушителя. Результаты определения размеров нарушителя в соответствии с рис. 4б также хорошо совпадают с аналогичными размерами модели. Рис. 4. Линии уровня результатов восстановления двумерной функции пропускания объекта /7 (х, у) а) - при проходе нарушителя «в рост»; б) - в положении «согнувшись», при учете только горизонтальной части тела нарушителя При использовании модели человека – нарушителя при пересечении им зоны охраны в положении «согнувшись» в виде комбинации двух эллиптических цилиндров, моделирующих горизонтальную и вертикальную части нарушителя, получены результаты, приведенные на рис. 5. В соответствии с ними контуры радиоизображений объекта совпадают с контурами используемых моделей нарушителя при пересечении зоны обнаружения в положении «согнувшись». Отсчет длины горизонтальной части нарушителя (по координате x) дает значение 1…1,1 м; высота горизонтальной части нарушителя (по координате y) равна 0,4...0,5 м. Размер по координате x вертикальной части нарушителя составляет 0,2...0,3 м; по координате y – 0,6 м. Эти результаты близки к размерам используемой модели нарушителя. В заключение отметим, что при определении геометрических размеров нарушителя по обеим осям X и Y используется значение RH расстояния нарушителя от антенны ПРД, а при определении размера нарушителя по оси X – значение координаты X q нарушителя. Определение их значений может быть произведено аналогично используемым в просветных радиолокационных станциях методам. Предложенные алгоритмы получения теневых радиоизображений объектов позволяют сформировать контур нарушителя, по которому можно определить тип нарушителя и часть его геометрических размеров. Рис. 5. Результаты восстановления вида двумерной функции пропускания объекта р (х, у) при моделировании пересечения зоны обнаружения нарушителем в положении «согнувшись» при учете горизонтальной и вертикальной частей тела нарушителя а) - линия уровня двумерной функции пропускания при Г-образной модели нарушителя; б) - при Т-образной модели нарушителя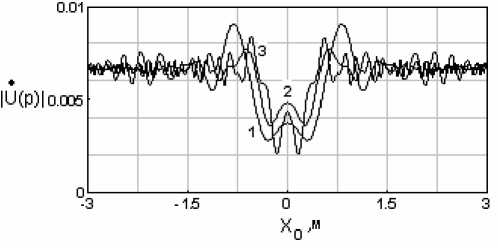
Список литературы О возможности формирования двумерных теневых радиоизображений нарушителей в охранных системах ближней радиолокации
- Оленин Ю.А. Двухпозиционные радиолокационные системы обнаружения ближнего действия: основы электродинамики формирования информационных признаков сигнала//Проблемы объектовой охраны. Сб. науч. трудов. Пенза: ИИЦ ПГУ Вып. 2, 2001. -C. 176.
- Борн М., Вольф Э. Основы оптики. М.: Наука, 1973. -720 с.
- Сороко Л.М. Основы голографии и когерентной оптики. М.: Наука, 1971. -616 с.
- Сальников И.И., Чернышев М.Н., Чернышев Н.И. Восстановление вида двумерной функции пропускания объекта в двухпозиционных РЛТСО//Современные методы и средства обработки пространственно-временных сигналов. Сб. материалов VII ВНТК. Пенза: ПДЗ, 2009. -С. 20-24.


