О возможности локализации волн Рс1 вблизи ионосферы с учетом наличия тяжелых ионов в магнитосфере

Работа посвящена исследованиям структуры УНЧ-волн в магнитосфере с примесью тяжелых ионов. Частота волн предполагается сопоставимой с гирочастотой ионов в магнитосфере. В случае наземных наблюдений это короткопериодические геомагнитные пульсации диапазона Рс1, включая так называемые «жемчужины».

В течение долгого времени основной была модель, согласно которой жемчужины представляют собой волновые пакеты, бегущие вдоль силовой линии и попеременно отражающиеся от разных полушарий [Гульельми, 1979; Demekhov, 2007]. Преимущественной областью источников этих волн обычно считается плазмопауза [Дмитриенко, Мазур, 1983; Dmitrienko, Mazur, 1985, 1992; Дмитриенко и др., 1986]. Однако недавние спутниковые наблюдения противоречат этой картине. Прежде всего, согласно модели бегущего волнового пакета с периодом повторения жемчужин связывают скачок пакета «вперед-назад», т. е. волновой пакет прошел путь вдоль всей силовой линии, отразился от ионосферы и вернулся. В этом случае зарегистрированный наземными установками период повторения жемчужин должен быть в два раза больше, чем регистрируемый спутниками в космосе. Однако этого не происходит: период повторения, наблюдаемый на земной поверхности, совпадает с наблюдаемым в космосе [Mursula, 2007].

Важным аспектом является наличие в магнитосфере Земли тяжелых ионов. В частности, ионов кислорода может быть так же много, как и протонов [Yang et al., 2010]. Поэтому учет такой примеси при описании среды распространения УНЧ-волн необходим. Добавление тяжелых ионов приводит к тому, что на силовой линии появляются области, прозрачные и непрозрачные для распространения волн. В этом случае волновой пакет может перемещаться только в областях прозрачности. Таких областей вдоль силовой линии несколько: резонатор, расположенный в экваториальной части силовой линии и ограниченный классическими точками поворота, а также две области, расположенные вблизи ионосфер разных полушарий, ограниченные верхней границей ионосферы с одной стороны и точками сингулярности с другой [Klimushkin et al., 2010; Мариловцева и др., 2010; Гульельми, 1967; 2007; Guglielmi et al., 2000; 2001; Guglielmi, Kangas, 2007]. Резонатор возникает в случае использования для описания структуры волн как квазипродольного приближения [Гульельми, 1967, 2007; Guglielmi et al., 2000, 2001; Guglielmi, Kangas, 2007], так и квазипоперечного [Klimushkin et al., 2010; Мариловцева и др., 2010]. Собственные частоты резонатора квантованы. В работах [Klimushkin et al., 2010; Мариловцева и др., 2010] предполагается, что экваториальный резонатор служит резервуаром энергии и определяет частоту возбуждаемой волны. Некоторая доля энергии волн проникает в области непрозрачности, отделенные от резонатора точками поворота. Было найдено, что за пределами резонатора для области непрозрачности существует одно спадающее решение, которое в результате описывает установление колебаний в приионосферной области проводимости.

Главной задачей данного исследования является выяснение вопроса, могут ли там возникать собственные колебания, т. е. имеется ли спадающее решение вблизи точки сингулярности, а также какая доля энергии теряется при прохождении волны через точку сингулярности.

Мы исходили из того, что вблизи ионосферы применимо приближение ВКБ, но при подходе к точке сингулярности ВКБ-решения становятся неверными. Поэтому область вблизи точки сингулярности необходимо рассматривать как область применения решений уравнения Бесселя. В области непрозрачности в окрестности точки сингулярности справедливы решения модифицированного уравнения Бесселя, вдали от точки сингулярности снова становятся допустимыми решения, полученные при помощи ВКБ-приближения.

Выкладки проведены для квазипоперечного распространения, однако полученные результаты справедливы и в случае квазипродольного распространения, поскольку резонатор и приионосферные области проводимости возникают в обоих случаях и имеют одинаковые свойства.

Система координат

Используем аксиально-симметричную модель магнитосферы. Вводим ортогональную систему координат {х1, х2, х3}, привязанную к магнитному полю. Здесь координатная поверхность х1=const совпадает с магнитной оболочкой, х2 отмечает силовую линию на магнитной поверхности, а координата х3 отмечает точку на силовой линии. Элемент длины в такой системе задается выражением dl2 = g 1( dx 1)2 + g 2( dx 2)2 + g 3( dx 3)2.              (1)

Здесь gi = gii (x 1, x3) - диагональные компоненты метрического тензора (недиагональные равны нулю в силу ортогональности системы). Детерминант метрического тензора записывается как g = g 1 g2 g3. Верхние и нижние индексы означают контравариантные и ковариантные компоненты вектора соответственно. Они связаны между собой выражением aj = aj I gj. «Физические» компоненты вектора (т. е. измеряемые в обычном евклидовом базисе) определяются как

aj

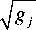
мирование по повторяющимся индексам здесь не подразумевается.

Продольная структура УНЧ - колебаний в приионосферной области при учете неидеально проводящей ионосферы

В работах [Klimushkin et al., 2010; Мариловце-ва и др., 2010] при исследовании приионосферных областей предполагалось, что ионосфера является идеально проводящей поверхностью для волны, в результате чего волна полностью отражается от границы ионосферы. Однако, так как геомагнитные пульсации наблюдаются на Земле, часть энергии волны все-таки проникает сквозь ионосферу. Именно поэтому случай, рассматриваемый в данной работе, важен для правильного описания структуры волны.

В последнее время появились свидетельства довольно сильной поперечной локализации волн Рс1 [Engebretson et al., 2002, 2008; Mursula, 2007; Yahnin et al., 2007], что соответствует большому значению поперечной компоненты волнового вектора, таким образом, рассмотрение волны в квазипоперечном приближении справедливо. В случае тороидально поляризованной волны, когда k i >>k 2, продольная структура УНЧ-колебаний в приионосферной области задается уравнением г                      ^

дз g дз + < £± —

I V g      g 1     c J

Ф = 0.

д

Здесь д3 = —3, е± - компонента тензора диэлек-дx трической проницаемости. Если частота волны существенно ниже, чем гирочастота электронов Ωce, а также присутствуют два типа ионов: протоны и тяжелые ионы, то тензор диэлектрической проницаемости записывается в виде е11 =

—ОО ,

22 pp             ph

2    ,-.2 + Г>2,^2 ’

“cp - ®  “ch - ® pe    ^‘cp ^‘pp      “ch ^‘ph

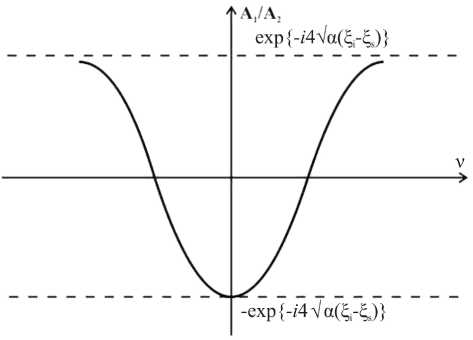
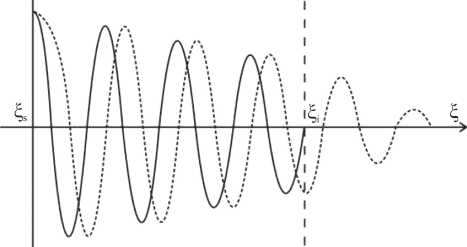
®QCC го “2d - го2 Ю “2. - Ю2 ’ ce              cpc где Ωp и Ωc – электронные (индекс e), ионные (h) и протонные (р) плазменная и циклотронная частоты соответственно, ω – частота волны. В случае полои-дально поляризованной волны (k1<

Заменим в уравнении (2) продольную координату x³на ξ следующим образом:

d ^ = jj^dx3, g2

в результате чего уравнение (2) примет вид

+V ©Ф = 0, ^д^

где V © = g²e_± —, ^g1     ^c2

здесь с – скорость света.

Решим это уравнение для области, заключенной между ионосферой и точкой сингулярности, используя ВКБ-приближение. В этом случае ВКБ-решение запишется как

^Ф= (V(<4^{eXP (}i^ “ ^d ^^{) + +}(V₍^yi4^exp(^-iJ 0#(!)^d^);

A1 и A2 – постоянные коэффициенты.

Перейдем к граничным условиям. В случае неидеально проводящей ионосферы граничные условия записываются в виде [Leonovich, Mazur, 1993]

фк

V± дФ । "TOax³   .

Здесь ξ_i – координата границы ионосферы, c² cos(x±)

v± =---=—— (знаки плюс и минус относятся к

4пХ р ионосферам разных полушарий), х – угол между силовой линией и вертикалью к ионосфере в точке их пересечения, а ^ р - интегральная педерсенов- ская проводимость ионосферы. Так как мы рассматриваем одну область проводимости с одной ионосферой и одной точкой сингулярности, а вторая область симметрична первой, мы вправе рассмотреть решение при граничных условиях только с одним знаком. В таком случае соотношение между коэффициентами

A1 = -A2 e "‘⁴^a^{(l -ls)}х

⁴®^(li ^{- l},)--g (i^{v - 4v} ^4^l-^)

M^{l -l}) ⁺—(iv^-4vVa⁴^i -^l) g₂

ξs – координата точки сингулярности. Зависимость соотношения коэффициентов от параметра ν представлена на рис. 1.

Решение (4) справедливо вдали от точки сингулярности. Вблизи точки сингулярности потенциал имеет вид

Рис. 1. Зависимость соотношения коэффициентов от параметра ν.

V (l) =

a

l-T

где a – положительная константа. В этом случае решение (4) будет иметь вид

Ф =

A (l-l,)1/⁴nДйа .

a ^1/4 e⁺

Atl-lF a1/4

e - ^- 2 7^a(I-ls)

Решение (6), полученное при помощи ВКБ-прибли-жения, несправедливо при нахождении в окрестности точки сингулярности. В этой области необходимо рассматривать уравнение (3) как неполное уравнение Бесселя. В таком случае его решение запишется как

Рис. 2. Зависимость волновой функции от продольной координаты в приионосферной области прозрачности при разных граничных условиях: сплошная линия – идеально проводящая ионосфера, штриховая – неидеально проводящая ионосфера.

Ф = (l-ls )1/2 X

х [ a Ji (2 Ta(l-l'j)+a 2 y (2 T^dFj)

где J1 и Y1 – функции Бесселя, a1 и a2 – коэффициенты. Вдали от точки сингулярности мы вправе вос-

пользоваться асимптотическим разложением для функций Бесселя. Таким образом, выражение (9)

перепишется в виде

Зависимости полученного решения от продольной координаты при различных граничных условиях показаны на рис. 2.

Выполнив аналитическое продолжение функции через особенность, получим структуру волны вблизи точки сингулярности:

^ф= a2 V^l-l_${11 (7a(^l-l_s))^X

Ф =

2 7лa1,4

( ai V

n г—

- e²a 2 IX

X

. 3n ,-----------

X e - ^-_T ei²

(5-5 )^1/4(      in ^

⁺ЧПО^" V ^a1^{+ e 2 a 2},

1 - e‘²e^-4 V^a(li^-ls> 0

1 + e ⁴e^-4^^a(l--55 * 0

,3л i—

+ e²

X

. 3n ----------- у ^z 4 ^-127^a(l-ls) /\ e    e •

-2/n [ K1 (27 a (l-ls))]}.

После сшивки этого выражения с решением (8), с учетом соотношения между коэффициентами (6), получим соотношение между коэффициентами a1 и a2:

a1 = - a₂

1  e‘2e "-⁴ V^a(li^-ls) 0

1 + e ⁴e"i⁴^^a(11 ^s) 0

где θ – выражение, стоящее в квадратных скобках из соотношения (6).

Здесь I1 и K1 – модифицированные функции Бесселя, a2 – амплитуда источника.

Чтобы найти поле в точке сингулярности, применим асимптотическое разложение для функций Бесселя при малых значениях аргумента. Таким образом, структура волны в точке сингулярности

Ф =

a ajl-l,) + ^^Tl-l lna(l-l.) . (12) nV a

Видно , что в точке сингулярности амплитуда волны конечна, хотя и имеет скачок. Коэффициенты a1 и a2 – те же, что и в (9).

Продольная структура волны в области непрозрачности

Исследование экваториального резонатора [Klimushkin et al., 2010; Мариловцева и др., 2010], в котором усиливаются УНЧ-волны, привело к выявлению следующих эффектов. Некоторая доля энергии волн проникает в области непрозрачности, отделенные от резонатора точками поворота. Спектр колебаний в резонаторе дискретен, частоты возбуждаемых волн определяются собственными частотами резонатора. Было найдено, что за пределами резонатора для области непрозрачности существует одно спадающее решение, которое в результате приводит к установлению колебаний в приионосферной области проводимости. Выкладки, приведенные в данном разделе, отвечают на вопрос о том, возможно ли существование такого спадающего решения вблизи точки сингулярности.

В области непрозрачности продольная структура волны описывается выражением

Φ= ξ-ξs×

получим соотношение между коэффициентами при данных граничных условиях:

a₁= a₂

где

×

a₁′I₁(2 a(ξ-ξ_s))

-2a2′K1(2 a(ξ-ξs)) π

Здесь a₁′ и a₂′ – постоянные коэффициенты. Из этого уравнения видно, что имеются два линейно независимых решения. Интересно проверить, возможно ли существование лишь одной моды, которая могла бы привести к генерации собственных колебаний в приионосферной области проводимости, и при каких граничных условиях такое спадающее решение может существовать. Поскольку с ионосферой граничит только область, описываемая ВКБ-приближением, необходимо совершить последовательно аналитическое продолжение функции в область обычных функций Бесселя и сшить его с решением ВКБ, таким образом выразив решение через коэффициенты A1 и A2. После чего, применив необходимые граничные условия, совершим обратные действия и получим соотношения коэффициентов a₁′ и a₂′ .

В качестве граничных условий рассмотрим два случая: ионосфера, обладающая большой проводимостью и малой проводимостью. В случае большой проводимости ионосферы

Φ ξi = 0, соотношение между коэффициентами

a₁= a₂

3π

I—

e²

3π

_1-e₂e-i4 a(ξ -ξ_s)

3π

₁₊e₂e-i4 a(ξ -ξ_s)

Из данного выражения видно, что в случае равенства нулю одного из коэффициентов второй тоже становится равным нулю. Таким образом, существование при заданных граничных условиях одного линейно независимого решения невозможно.

Проделав аналогичные операции в случае малой проводимости ионосферы:

dΦ dξ ξi = 0

3π

I— e²

3π

I —

1-e²

e-i4 a(ξ -ξ_s)ψ

3π

I — 1+e²

_e-i4 a(ξ-ξs)_ψ

ψ₌1-4i a(ξ -ξ_s)^1/4_. 1+4i a(ξ_i-ξ_s)^1/4

В этом случае также

видно, что существование одного решения невозможно. Поэтому можно заключить, что для области непрозрачности существуют и спадающее, и растущее решения, которые взаимно гасят друг друга, поэтому возбуждение собственных колебаний вблизи ионосферы невозможно.

Потери энергии при прохождении через точку сингулярности

Как уже было показано, при прохождении волны через точку сингулярности амплитуда волны возрастает до большого, но конечного значения и со стороны приионоферной области устанавливаются устойчивые колебания. Интересно посмотреть, что же происходит с энергией при прохождении волны из приионосферной области в область непрозрачности. Для исследования потери энергии в точке резонанса рассмотрим средний поток вектора Пойнтинга [Ландау, Лифшиц, 2005]:

— с — -^*

S = — Re E, B 8п L

Рассмотрим волну, распространяющуюся в продольном направлении (слева направо, из приионо-сферной области в область непрозрачности). Тогда (16) преобразуется в

S3 = ^c Re(E1,B2^∗).                             (17)

8π

Применив ВКБ-приближение к компоненте электрического поля

E₁= -ik₁Φ,

вычислив компоненту магнитного поля из уравнений Максвелла

B₂^∗= -k₁^c ∂₃Φ^∗, ω

получим выражение для вычисления потока вектора Пойнтинга

S 3 = — Re ^jУс 2 c (Ф, д₃Ф)[. 8п    I ¹m^v

Справа вблизи точки особенности волновая функция [Klimushkin et al., 2010; Мариловцева и др., 2010] имеет вид

Φ = a₀πe^-π/4 sin S₀×

X ^(5-5,)lna(5-5)-

П                 nV a

где a0 – амплитуда источника, S0 – фаза. Подставив данное выражение в (18), получим

S з = 0.

Слева от точки особенности выражение для волновой функции получается с помощью процедуры прохождения через особенность. Здесь функция имеет вид

Ф = a₀ Vne^л/4 sin 5₀X

X — (К ){ln a U4s ) + i^n}1= П                     nJ a

Поток вектора Пойнтинга будет определяться выражением

Sз = ——k2a2 sin²S_n g²^X

8лю ¹⁰    07g

^X [(^^-^s )^{{1 + 2}a^lna U^-5s)^{} -}1].

Из выражения (21) видно, что поток вектора Пойн-тинга слева от точки сингулярности не равен нулю и направлен вдоль увеличения координаты. Это означает, что волна, распространяясь в приионосферной области проводимости, при переходе через точку сингулярности полностью затухает; происходит полное поглощение энергии волны. Таким образом, в точке сингулярности происходит процесс, сходный с альфвеновским резонансом.

Заключение

Было найдено, что невозможно возбуждение собственных колебаний в приионосферных областях. В области непрозрачности невозможно существование одного спадающего решения, которое описывает структуру волны, что могла бы оказывать влияние на колебания в резонаторе. Таким образом, получаем следующую картину: в экваториальной части силовой линии имеется резонатор, ограниченный точками поворота, которые отделяют резонатор от областей непрозрачности. В этих областях волна затухает, однако, если энергия волны достаточно велика, часть волны может туннелировать сквозь области непрозрачности и проникать в приионосферные области проводимости. Проходя через точку сингулярности, волна претерпевает что-то вроде альфвеновского резонанса, и в область проводимости попадает волна с уже большей амплитудой. В ионосфере волна постепенно затухает. Частота колебаний волны определяется собственными частотами резонатора. Так как собственные частоты резонатора квантованы и довольно близки друг к другу, формируются биения, структура которых очень близка структуре жемчужин.

Работа выполнялась при поддержке программы № 4 Президиума РАН, программы № 15 Отделения физических наук РАН и программы № 9 Отдела наук о Земле РАН. Автор выражает признательность Д.Ю. Климушкину за постановку задачи и ценные замечания, а также П.Н. Магеру за многочисленные обсуждения.