О возможности применения изоэнтропийного уравнения состояния жидкости к стеклообразным веществам

Путем модификации изоэнтропийного уравнения состояния жидкости применительно к стеклообразным веществам получено соотношение, которое находится в согласии с экспериментальными данными для свинцовосиликатных стекол. Плотность энергии акустического поля линейно зависит от внутреннего давления этих систем.

About possibility of application of the isentropic equation states of a fluid to vitreous substances1

By modification of an isentropic equation of state of a fluid with reference to vitreous substances the relation which is in the consent with experimental dates. The density of energy of the audio field linearly depends on intrinsic pressure of these systems

Жидкое состояние является промежуточным между твердым и газообразным состояниями. Если для газов и кристаллов имеются упрощенные модели, соответствующие предельным случаям - идеальному газу и идеальному кристаллу, то для жидкостей не существует такой простой модели, на основе которой можно было строить теорию. То же самое можно сказать относительно стеклообразных твердых тел. Ввиду беспорядочного расположения атомов и отсутствия дальнего порядка в структуре жидкостей и стекол прямые дифракционные методы применительно к ним оказались малоэффективными. Лишь для кристаллов разработаны эффективные структурные методы и достаточно строгие теории [1, 2].

Поэтому в настоящее время по-прежнему остаются актуальными приближенные модельные подходы к природе жидкостей и стекол. Среди них, несомненно, заслуживает внимания концепция Белинского [3, 4], согласно которой основное состояние жидкости представляет собой бозе-конденсат квазичастиц акустической природы, изоэнтропийное уравнение состояния которого имеет вид pv^F^P,^, (I)

где Pi - внутреннее молекулярное давление, обусловленное силами межатомного (межмолекулярного) притяжения, Р - внешнее давление, р - плотность, г₅- адиабатическая скорость звука, Г_й0 - постоянная, которая вдали от области фазовых переходов практически не зависит от давления и температуры. В этом смысле Г_а„ относится к параметрам класса постоянных Грюнайзена и называется нелинейным акустическим параметрам. Он характеризует взаимодействие акустического поля жидкости с веществом.

Для изотермического случая уравнение (1) записывается в виде pv^HP. + P), (2) где vr - изотермическая скорость звука, ^ = yvf у - отношение теплоемкостей (Q/Q,), Г = Гад/у - некоторая постоянная.

В настоящем сообщении приводятся предварительные результаты применения уравнения (2) к стеклообразным твердым телам.

Структура стекла в отличие от кристаллического твердого тела представляет собой фактически замороженную неупорядоченную структуру соответствующей жидкости. Поэтому в первом приближении стекла структурно неотличимы от жидких

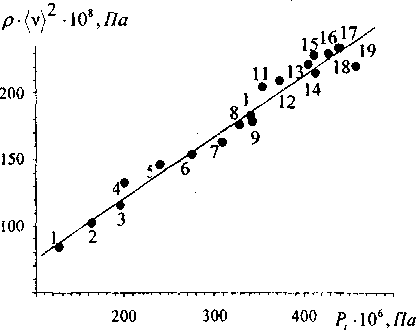
Рис. 1. Корреляция между плотностью энергии акустического поля p(_vy и максимальным внутренним давлением Р, свинцово-силикатных стекол \Р ~ 1 am, t = 2(Р С). Содержание РЬО, мол.%: /-2.78; 2-5.5; 2-8.28; 4-10.51; 5-13; 6-15.4; 7-17.95; 8-19.65; 9-20.5; /0-21.4; /2-22.8; /2-24.2; /5-25.06; /4-27.3; /5-29.8; /6-31; /7-32.5; 18-ЗАЛ; /9-37.25.

расплавов. Различие стекла от расплава заключается в наличии некоторого “заморо-женного” конфигурационного беспорядка [1, 2]. Кроме того, если в жидкостях возможно прохождение только продольной звуковой волны, то в стеклах (как и в любых твердых телах) распространяются как продольные, так и поперечные акустические волны.

Поэтому в уравнении (2) в случае стекла следует брать среднюю квадратичную скорость (у), которая не зависит от на правления распространения звуковых волн [5]

где v, и v, - скорости продольных и поперечных волн, соответственно. В качестве внутреннего давления в первом приближении можно использовать максимальное внутреннее давление, определяемое из данных о модуле упругости £ и коэффициенте Пуассона (коэффициенте поперечной деформации) [1,6]

пределах от 20 до 70 мол.% [7]. Введение РЬО в кварцевое стекло SiO₂ приводит к разрушению пространственного сеточного каркаса ковалентных связей и образованию полярных группировок. Происходит разрыв мостиковых связей -Si-0-Si- и их число уменьшается [8].

Использованные нами экспериментальные данные о величинах р, v, , v, , Е, ц относятся к комнатной температуре 20°С и атмосферному давлению Р ~ 10⁵ Па (1 ат.) [7]. В твердых телах и жидкостях внутреннее давление, обусловленное силами сцепления между частицами, оказывается порядка Pj~ 10⁹ - 10¹⁰ Па (10⁴ - 10⁵*оти). Поэтому в рассматриваемых условиях по сравнению с внутренним давлением можно пренебречь внешним атмосферным давлением Р ~ 1 ат, сжимающим систему извне: Р, »Р. В рамках нашего приближения уравнение Белинского (2) применительно к стеклообразному состоянию принимает следующий вид:

Р^ = ГР, . (5)

Поскольку величина Г по Белинскому [3, 4] является константой, зависимость p{v}² от р должна быть линейной. Как видно из рисунка, указанная зависимость в координатах p^v) -Д для свинцовосили-катных стекол выражается прямой линией, что подтверждает наше предположение.

Прямая на данном рисунке описывается эмпирическим соотношением р^* = 0.456/; + 29.4.

Таким образом, полученные предварительные результаты подтверждают возможность применения изоэнтропийного уравнения состояния жидкости к стеклообразным твердым телам. В дальнейшем необходимо провести более детальное исследование в этом направлении, в частности, представляет интерес обоснование данного подхода в рамках модели возбужденного состояния жидкостей и стекол [9].