О возможности применения модели фазового поля для описания структуры фронта кристаллизации расплава

Классический подход к моделированию фазового перехода первого рода включает отслеживание границы раздела фаз, которая отделяет растущую фазу от исходной (материнской). Это требует решения весьма непростой задачи со свободной границей раздела фаз, положение и форма которой является частью решения (задача Стефана).

Классическая модель Стефана не учитывает влияние таких физических факторов, как поверхностное натяжение расплава и концентрационное переохлаждение. Учет этих явлений приводит к изменению температуры на поверхности раздела, которая теперь становится неизотермической. При этом различать две фазы лишь по температуре невозможно, а, значит, невозможно применять энтальпийный подход, исключающий явное отслеживание фронта.

В ряде работ предлагается иной подход [1-7], основанный на введении на мезоуровне поля параметра, характеризующего отклонение системы от равновесия. Фазовый переход рассматривается как изменение этого поля, называемого параметром порядка или параметром фазового перехода. Изменение параметра порядка в каждой точке сопровождается выделением тепла, которое, в свою очередь, влияет на скорость этого изменения. Такой подход реализуется в рамках так называемой модели фазового поля (МФП), согласно которой вводится новая переменная - фазовое поле ϕ , принимающее постоянные значения в каждой из фаз: ϕ =0 в твердой и ϕ =1 в жидкой фазах. Переход от жидкой фазы к твердой происходит в узкой переходной области, где ϕ плавно меняется от 1 до 0. Поэтому МФП дает подходящую основу для численного решения сложной задачи кристаллизации без явного отслеживания движения границы раздела фаз; при этом граница, по аналогии с энтальпийным подходом, определяется апостериорно как изолиния ϕ =0,5 фазового поля .

Введенная переменная определяется из рассмотрения задачи микроуровня с применением статистической термодинамики [1], допускает существование жидких участков, переохлажденных или перенасыщенных, и учет влияния кривизны фронта.

МФП базируется на последовательном термодинамическом рассмотрении задачи мезоуровня, в предположении, что термодинамические функции в каждой точке зависят не только от значения параметра порядка в этой точке, но и от компонент градиента этого параметра. Такое уточнение необходимо при рассмотрении межфазных границ, где градиенты параметра велики [2] .

Идеи МФП впервые описываются для затвердевания чистых металлов в работах А.Р. Уманцева, А.Л. Ройтбурга [2], G. Caginalp [4] и для близкой по сути антифазной граничной миграции - в работах S.M. Allen, J.W. Cahn [5]. O. Penrose, P. Fife [1] сформулировали условия, по которым уравнения для фазового и температурного полей выводятся из термодинамически обоснованного для фазового перехода I-го рода функционала энтропии.

В данной работе исследуются возможности МФП для описания структуры твердой фазы вблизи границы раздела затвердевающего чистого металла на примере одномерной тестовой задачи, сформулированной в рамках последовательного термодинамического рассмотрения [6].

Теоретические основы метода

Рассмотрим закрытую систему объема V (мезоуровень), в котором чистый металл претерпевает фазовый переход I-го рода ( L-S). Параметр порядка ф ( г , t ), называемый фазовым полем, определяет фазу материала в точке r ; ф =0 в твердой фазе, ф =1 - в жидкой. Узкая область (с шириной, стремящейся к нулю), в которой 0< ф <1, соответствует межфазной поверхности раздела. Для простоты предположим однородность плотности среды по всей системе, отсутствие конвекции в жидкости; полагаем, что система находится в механическом равновесии.

Внутренняя энергия Е любого подобъема Qc V представляется соотношением

E- J ed Q ,                                   (1)

Q где е - удельная (на единицу объема) плотность внутренней энергии.

Согласно I закону термодинамики изменение Е со временем подчиняется соотношению:

E + J q ■ n d ( dQ ) = 0,                             (2)

dQ где dQ - поверхность Q с внешней нормалью n, q - поток внутренней энергии. Используя (1) и теорему Остроградского-Гаусса, соотношение (2) преобразуем (с учетом произвольности выбора объема Q и гладкости поля q) к виду e + у. q = 0.                                   (3)

Далее предположим,  что энтропия произвольного подобъема Qc V представляется функционалом

S - J [ 5 - 2 е ² ( Уф ) 2 ] d Q ,                                 (4)

Q где 5(e,ф) - плотность энтропии (расширение классической термодинамики, где 5 = 5(e,р), но плотность здесь полагается постоянной); e=const (для случая изотропии поверхностного натяжения). Такой вид функционала предлагается по аналогии с теорией Ландау-Гинзбурга для фазового перехода II-го рода [7]. Второе слагаемое в (4) отражает зависимость термодинамического потенциала не только от значений термодинамических переменных, но и от их градиентов (в частности, Уф ).

Дифференцируя (4) по времени и подставляя выражение (3) для e & , получим

S-J

Q

U e )

e +

д 5 ]      _{2 2}

— I + е ² У ² ф ф d Q ^дф<

ф

-J dQ

q + е ² фУ ² ф

e

■ n d ( dQ ) .

II закон термодинамики утверждает, что в любом Qc V производство энтропии положительно. Это производство может быть вычислено выделением из S потока энтропии через границу 5Q . Тогда производство энтропии имеет вид

Q

5 5 5ф

.V2 Ф]фг dQa 0,

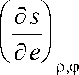
для потенциала 5 = 5 ( e , р,ф )).

где Т - абсолютная температура ( — =

Таким образом можно гарантировать локально положительность производства энтропии, выбирая

I 5 5 |                                     .5 5 5 | q = MVl — I = MTVl—1,      тф = |—l+e2 V2ф,                  (7)

<5 e J         V T J           к5ф7

ф                                        e где MT и т - положительны. Тогда управляющие уравнения примут вид:

• •    для плотности внутренней энергии

e = -v-

Mт Vl - I

^T V t J

• •    для фазового поля

1 / A

1 d e I тф = -- — I + c2 V2ф .

^T W S

Для определения производной в (9) используется плотность свободной энергии

I ^d e I                                                              I ^{d e}

Гельмгольца: df = - 5dT + l I d ф . Тогда, учитывая, что de = Tds + l—— d ф , при

<дф> S                                          S постоянном s получим

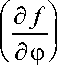
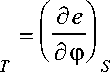
и

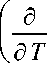
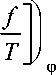
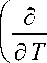
Последнее можно проинтегрировать при ф =const

5 T f (T, ф) = T - J

^V   Tm

e fc, ф)

dg + G (ф)

?             J

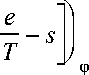
e

T 2 .

где G(ф) - произвольная функция интегрирования; TM - температура плавления. Предположим, что начальная плотность энергии имеет вид e = es(T) + p(ф)L(T) = eL(T) + [p(ф)-1]L(T) = eL(TM) + c(T-TM) + [p(ф)-1]L(T), (12) где eS(T) и eL(T) - классические плотности внутренней энергии твердой и жидкой фаз соответственно; L(T) = eS(T)-eL(T) - их разность. Здесь р(0)=0, р(1)=1; L0(T)=L(TM) - скрытая теплота плавления.

С учетом (12) плотность свободной энергии в (11) примет вид

I T f ( T , ф ) = T - J

V Tm

-L^d ;- [ p ( ф ) - 1 ] Q ( T ) + G ( ф ) ,

T L ( ? ) где Q ( T ) = J ^d g .

Tm ^

Заметим, что Q(T M ) = 0. Из (10), (13) получим

5 f I    5 5 e I        dp dG ( ф )

| =l— | =- T-^Q ( T ) + T—— 5фУ   <дф7       d ф          d ф

= - TQ ( T ) p ' ( ф ) + TG ' ( ф ).

Таким образом, управляющие уравнения (8), (9) примут вид

{ с + [ p ( _Ф ) - 1 ] L '( T ) } ^{d T} + l ( т ) p '( _ф ) |ф = к у ² т ,                       (15)

тф = Q ( T ) p ' ( ф ) - G '( ф ) + е ² V ² ф ,                                     (16)

где к= M_T / T ² = const коэффициент теплопроводности.

Выберем функцию р(ф) в виде ф J g (О d- p (ф) = 1-------= ф3(10 - 15ф + 6ф 2),    где    g (ф) = ф 2(1 -ф)2.          (17)

J g ⁽ - ) d -

Эта функция удовлетворяет условиям нормировки: p (0)=0, p (1)=1, а также условиям минимума потенциала свободной энергии независимо от Q ( T ), так как p ' ( ф ) = p "( ф ) = 0 при ф =0 и ф =1.

Потенциал / должен иметь локальные минимумы по ф при ф =0 и ф =1 для любых значений температур Т ; кроме того f непрерывен по Т в точке плавления. Эти ограничения на / и выбранный вид функции р ( ф ) (17) требуют, чтобы G ( ф ) также имел минимумы при ф =0 и ф =1; поэтому G ( ф ) выбирается симметричным относительно ф=1/2 , «W - образным» потенциалом в форме 1

G ( ф ) = —g ( ф ),     а > 0 , a=const .                        (18)

• 4 a

Выбор функции в виде полинома четвертой степени обусловлен простотой аппроксимации функции, имеющей два минимума.

В [6] показана связь параметров а и е с материальными параметрами:

я Г             Т^т-Т d ф)² ^⁸ Тм                  ,,_т

• ⁸ = V a е          °=1^{е т} м I = ...—,                       ⁽¹⁹⁾

• ^J V dx у 12 а

  -ю

где 8 - толщина фронта (является подгоночным параметром модели); ст - поверхностная энергия на единицу площади (для одномерной задачи), которая является отклонением свободной энергии от f ( T M , ф ).

Получим уравнения в безразмерном виде. Для этого введем масштаб длины: w - размер расчетной области, (w2 /к) = (w2 /к) с температуры по области, где к/с = к = const Тогда

• -    характерное время распространения

• -    температуропроводность в жидкости.

  x

  -—'

  x = —;

  w

  
  

  ~

  
  

  t

  
  

  t = ( w ²/к ) ^;

  
  

  _ T - Тм

  ^U   T m - T >,

  
  

  где Т з - некоторая температура на внешних границах, задаваемая в условиях Дирихле. В безразмерных величинах управляющие уравнения примут вид

  
  

  <

  
  

  ~

  L ‘ ( u ) 1 5 u

  ^~ ⁺ 5 1

  
  

  S

  
  

  ~z X

  L ⁽ U )       5ф ~₂

  -у- p ' ( ф )т~ = ^{V u} , о         d t

  
  
  
  

  ~² дф

  
  

  ~

  
  
  
  

  ~ m d t

  
  

  = e ^{2 у 2} ф+ ец S^{Q ( u} ) p ^{, (} ф ) ^- ^ g ‘ ( ф ),

  
  

где    ~( u ) = LL 0 , Q ~⁽ u ) = J  ---------------- —y d s ,

0 { 1 + [( T m - T >),' T „ ] s }

2ww [ L ₀ ] ^{2 а}= 12 c о Tm ’ Для простоты выберем

c ⁽ T M - T ) т , L 0

теплоемкость на

~ 5 е= — ,

w

m =-----...

^тк T M

.

единицу объема твердой фазы, равной ~

постоянной величине теплоемкости жидкости; L ( T)=L ₀ , тогда L ( и ) = 1. Также предположим, что T M - T ₀| <<  T M (это соответствует малому переохлаждению расплава), тогда согласно (21) Q(и ) = и .

Таким образом, уравнения (20) примут вид

£ ' ( и ) = 0 , p ‘ ( ф ) = 30 ф ²(1 - 2 ф + ф ²) = 30 g ( ф ),

д и 30 g ( ф ) дф д ~

д t

= V2и,

е ² дф ₉                          1

—   = е ² V ² ф + 30 g ( ф ) е a Su -- g '( ф ) .

m д t                          4

Отметим достоинства приведенной модели (23). Во-первых, модель согласуется с принципами термодинамики необратимых процессов, так как она получена из функционала энтропии, который является подходящим термодинамическим потенциалом в неизотермическом случае. Во-вторых, она построена так, что соотношения ф =0 и ф =1 соответствуют объемным твердой и жидкой фазам, независимо от температуры; это значит, что общее количество скрытой теплоты выделяется только в области границы раздела.

Рассмотрим эту модель более подробно.

Пространственно однородная задача

Рассмотрим постановку, не учитывающую изменение переменных по пространственным координатам (по аналогии с тем, как это делается для химических реакций в предположении эффективного перемешивания среды). Хотя данное предположение почти не физично для смеси твердой и жидкой фаз в кристаллизующемся расплаве, решение такой задачи позволит проанализировать нелинейность системы.

Итак, постановка пространственно однородной задачи имеет вид du 30g(ф) dф          е2 dф

+           = 0 ,              = 30 g ( ф ) ~ a Su -- g '( ф );

at S at          m dt4

ф(0) = ф0, и(0) = иa; g(ф) = ф2(1 -ф)2 .

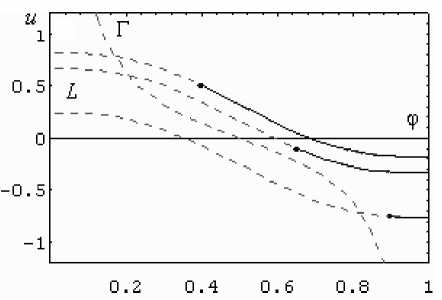
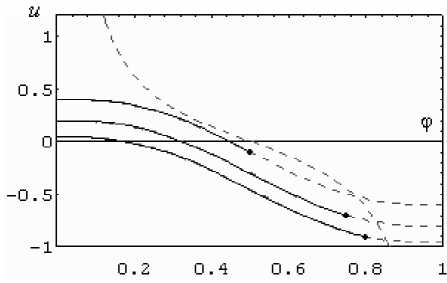
Решение системы получено методом Рунге-Кутта. На рис.1 приведены зависимости ф ( t ), полученные при различных начальных условиях. На рис.2 изображены соответствующие фазовые диаграммы.

На рис.2 изображены пунктирные кривые:

L - интегральные кривые при различных начальных условиях (24 1 ):

и ( ф ) = S [ J ( ф ) - J ( ф 0 ) ] + и 0 , где J ( ф ) = 10 ф ³ - 15 ф ⁴ + 6 ф ⁵;

Г - кривая, соответствующая стационарному решению (24 2 ):

^дф = 0 _{;   (} ) = g '( ф )      =     1 ф ^{(1 -}ф ^{)(1 -} 2 ф )

д t    ’    ф    120 ea Sg ( ф ) 60 е a S ф ²(1 -ф )²

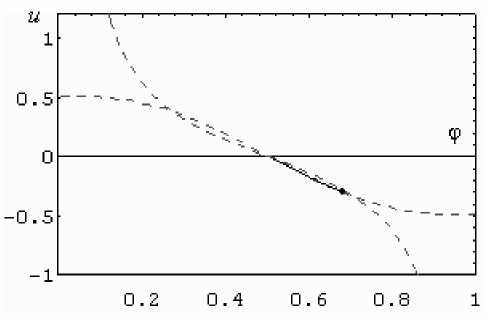
Решения системы изображены сплошными линиями, частично совпадающими с кривыми L , начальные условия отмечены точкой на соответствующей кривой.

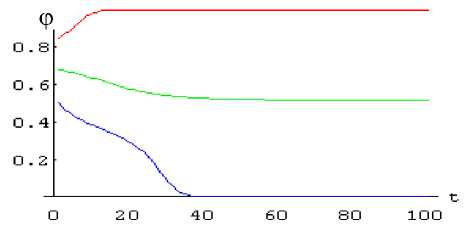
ϕ

0     20    40    60    80    100

Рис.1. Зависимости ф ( t ) для различных начальных условий

б

а

в

Рис. 2. Фазовые диаграммы системы (24) для различных начальных условий

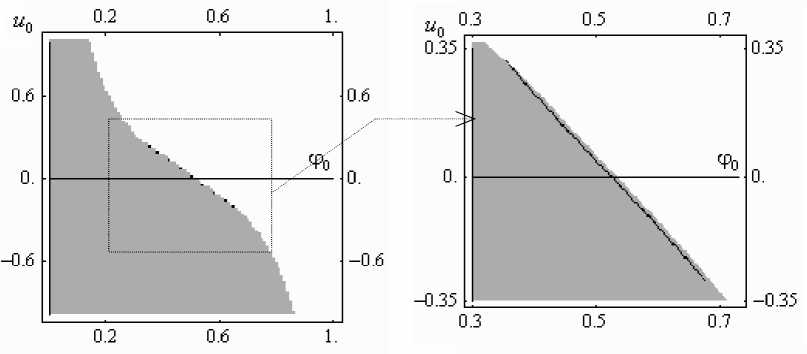
а                                             б

Рис.3. Области притяжения стационарных решений для различных начальных условий: а - ф ₀ е [0,0; 1,0], и ₀ е [ - 1,0;1,0]; б - ф ₀ е [0,3; 0,7], и ₀ е [ - 0,35; 0,35] ;

■ - ф = 0.0; □ - ф = 1.0; _н - ф = 0,5

Анализ устойчивости линеаризованной задачи

Вернемся к постановке задачи (24), которая для одномерного случая имеет вид:

ди 30g(ф) дф д2и ^~ +                      — —'■'                  , дt      S д t   5^2

g ² дф ₂ д ² Ф                     1

--=^—2 —у + 30 g ( ф ) ^— a Su - — g '( ф ) , m д t      д^ ²                     4 ^{6 v 2}

где £ - расстояние от фронта. Дополним ее начальными и граничными условиями:

и (0, ^ ) = и о® , ф (0, ^ ) = ф о ( ^ );

ф ^ 0, 2 ^ -го ; ф ^ 1, 2 ^ +го ; и ^ и , 2 ^ -го ; и ^ и , 2 ^ +го .

Исследуем устойчивость системы к малым возмущениям для того, чтобы установить спектр волновых чисел неустойчивых мод возмущений. Для этого линеаризуем уравнения (25), заменив функцию 30g(ф) ее средним значением на интервале [0,1]:

(30g(ф)) = ц—0 j g(ф)dф = 1. Кроме того, разложим в ряд вблизи точки ф0 функцию g’ (ф), сохранив только линейный член: g,(ф) = g'(ф0) + g"(ф0)(ф - ф0) + o(ф - ф0) •

Рассмотрим устойчивость линеаризованной системы по отношению к малым возмущения стационарных решений: ф ( t , £ ) = ф ( t , £ ) -ф ₀( ^ ) , u(t , £ ) = и ( t , £ ) - и ₀( ^ ) . Функции начальных условий удовлетворяют линеаризованной системе уравнений (25):

д ² и_п

—Г = 0, д^ ²

—

₂ д² ф              1

+ еа Su - 4 g ^,( ф 0 ) = 0;

вычитая (27) из (25), получим уравнения и начальные условия для пульсаций:

д U дф —* — * д t д t

д и

g ² дф

. —

,          —

д^2    m д t

= g ²

д ² ф         _Л 1

—у + —a Su--g"(ф0)ф , д^           4

и (0) = 0, ф (0) = 0, граничные условия: ф ^ 0, и ^ 0 , 2 ^ -го ;

$

$

Пусть ф ( t , £ ) = Ф e ^ш^^+ц t , u ( t , £ ) = U e ^ш^^+ц t , тогда, подставляя эти выражения в (28), получим систему линейных алгебраических уравнений относительно Ф и U :

Ц

( ц + го ²) U + S Ф = 0,

<

Г —2 — — аSU + —ц+—2 го

—

у m

2    g "(ф 0 ) '

4 У

Ф = 0.

Условия существования нетривиального решения последней приводят к квадратному уравнению относительно ц:

— 2

^е 2 | ~ 2 2 ^{1 +} m _— g ^{( ф} 0 ) |     | ~ 2 4

ц +1 g го + g а -    " I ц + I g го m V m           4 У у

-

го

g "⁽ф 0 ) )

4 J

=0

или а ц ² + b ц + c = 0,

решая которое получим зависимость декремента затухания возмущений ц от волнового числа го . Неустойчивыми будут возмущения с теми волновыми числами, при которых действительная часть корней уравнения (29) больше нуля: Re ( ц )>0.

Базируясь на обычных методах решения задач с параметрами для квадратичного трехчлена, исследуем возможное расположение корней квадратного уравнения (29).

Пусть D = b²- 4 ас >0, тогда корни уравнения ц и ц ₂ действительны и Re ( ц )= ц .

1. ц 1<0< ц 2 , если c < 0 , то есть			2 g "(ф о ) . to<  4~2 ;
	' D >  0;		' D >  0;
2. Ц 1 , ц 2<0, если 5		b — <  0; ^ ( 2 a	e	2 2 . 1 ~ 2 2 . ~ g to + e to + е a — m	" (ф о ) n        2 g " ( ф 0 ) 4   > 0; « ю >       ;
	c	> 0;	4	e 2 to 2 — g " ( ф о ) >  0;
		' D >  0;		' D >  0;
3. ц , ц 2 >0 , если	5	b —— > 0; « 5 2 a		i ~ 2   2 . 1 ~ 2 2 . ~ e to + e to + e a — m	g"( ф 0 ) n ,   <  0; ^ to e0 . 4
		c >  0;		[ 4 e 2 to 2 — g "( ф 0 ) >  0;

Дискриминант D уравнения (29) является биквадратным полиномом относительно to с положительным коэффициентом при to ⁴ .

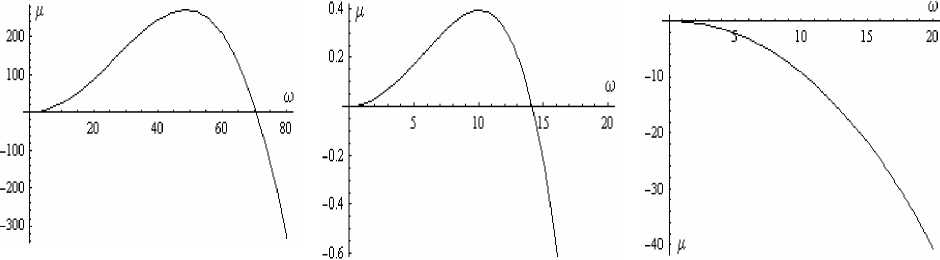
После того, как установлены общие зависимости знаков корней уравнения (29), рассмотрим частный случай на примере чистого железа, где параметры a , S , m , е определены согласно (22). Необходимые для их вычисления физические константы приведены в таблице. Для таких констант дискриминант уравнения (29) всегда положителен и уравнение имеет только действительные корни цщ = ц ( to ² ; ф о ). На рис.4 приведены зависимости p = p ( to ) при различных значениях ф ₀ .

Таблица

Физические параметры чистого железа

L 0 , Дж кг	C L , -Дж-кг o К	a , Дж м	T m , 0 К	к , м	w	т
272 103	922	20,4	1808	3,7 10-6	1	1

а                             б                             в

Рис. 4. Зависимости декремента затухания ц от волнового числа возмущения to:

(а) - ф о = 0,0; ф о = 1,0; (б) - ф о = 0,2; ф о = 0,8; (в) - ф о = 0,5

Итак, система устойчива к возмущениям с очень маленьким (порядка 10^-5 - 10^-4) и достаточно большим (порядка 15 - 75) волновым числом. При ф ₀ = 0,5 система устойчива к любым возмущениям.

Таким образом, с помощью линейного анализа устойчивости установлены спектры волновых чисел неустойчивых возмущений. Однако линейный анализ не отвечает на вопрос, какие из этих возмущений будут развиваться с наибольшей скоростью. Возмущения, растущие с наибольшей скоростью будут определять характерный размер структуры на фронте кристаллизации; для того чтобы их определить, рассмотрим тестовую одномерную задачу (24). В качестве начальных условий возьмем функцию фо(^)= 2

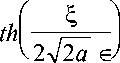
+1

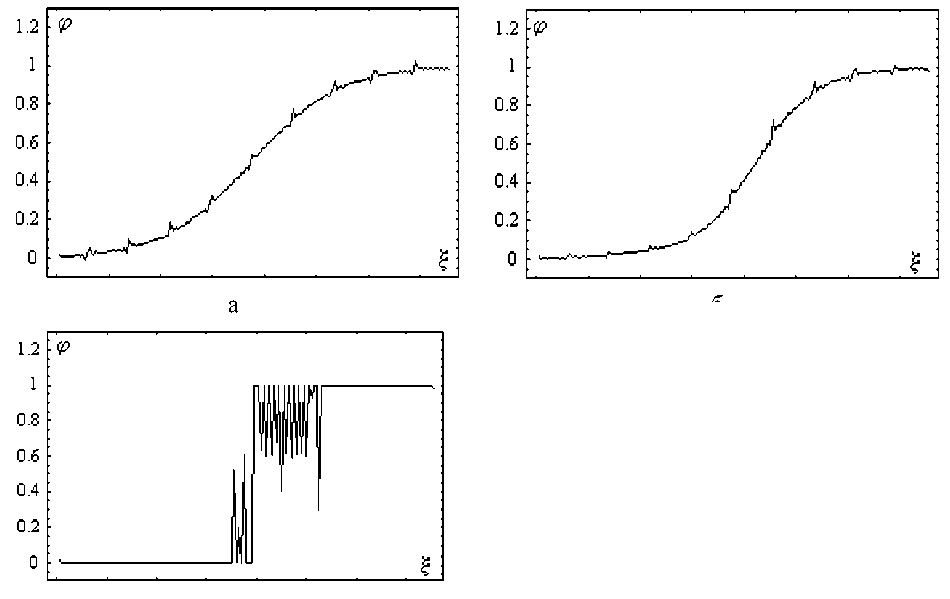
которая является аналитическим решением (24 2 ) при равновесных условиях и с условиями на границах ф ^ 0 , ^ ^ -да ; ф ^ 1, ^ ^ +да , с наложенными на нее неустойчивыми возмущениями в виде суммы синусов и косинусов. Результаты расчетов приведены на рис.5.

в

Рис. 5. Эволюция неустойчивых возмущений:

(а) - начальное распределение;

(б - г) - развитие возмущения определенной частоты с течением времени

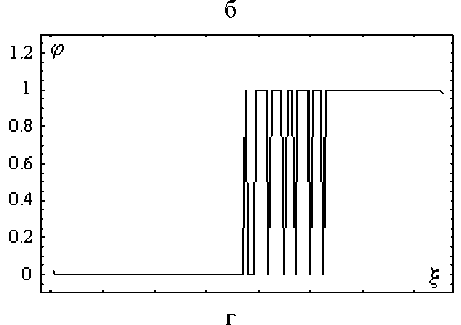
Из рис. 5 видно, что на начальном этапе происходит некоторое сглаживание возмущений, однако затем вблизи фронта кристаллизации, то есть в области, где параметр фазового поля меняется от 0 до 1, начинают расти возмущения определенной частоты. Это можно рассматривать как появление в жидкой фазе твердых частиц, то есть зоны смеси твердой и жидкой фаз. Расположение и характерный размер частиц твердой фазы определяются по изолинии ф =0,5. Заметим, что твердые частицы достаточно устойчивы (при расчетах картина на рис.5,г не меняется с течением времени).

Выводы

В работе рассматривались уравнения модели фазового поля, которые анализировались (как нелинейная система) с точки зрения их возможности описывать процесс структурообразования на границе раздела фаз при кристаллизации расплава.

При рассмотрении пространственно однородной задачи установлено, что система в зависимости от начальных условий имеет три стационарных решения; определены множества начальных условий, при которых получаются эти решения.

Из анализа устойчивости одномерной линеаризованной задачи получен спектр волновых чисел неустойчивых возмущений, эволюция которых исследовалась численно.

Установлено, что в процессе эволюции возмущений вблизи границы раздела в жидкой фазы появляются частицы твердой фазы, которые не исчезают с течением времени. Характерный размер и положение твердых частиц определяются по изолинии фазового поля.

Работа выполнена при поддержке гранта Министерства образования в области металлургии