О возможности применения пассивного метода снижения сопротивления лёгких самолётов

Пассивный метод снижения лобового сопротивления цилиндрических тел за счёт установки дополнительных тел вблизи цилиндрической поверхности применим в разных областях техники, например в авиации, в строительстве зданий, мостов, газо- и нефтеперегонных труб или мачт ветрогенераторов. Результаты численного моделирования и эксперимента [1-4] показали эффективность метода снижения лобового сопротивления цилиндрических тел за счёт установки плоской разделительной пластины сзади и дефлекторов

«Московский физико-технический институт (национальный исследовательский университет)», 2024

спереди вблизи их поверхностей. Подтверждён ранее обнаруженный эффект снижения лобового сопротивления цилиндра [3] с применением жёстко связанных между собой дефлекторов перед цилиндром и задней разделительной пластины [1, 2, 4], имеющих возможность поворачиваться вокруг оси цилиндра. Разделительная пластина обеспечивает ориентацию системы дефлекторов по направлению набегающего потока и снижение пульсаций в аэродинамическом следе за цилиндром. Установлено, что сопротивление системы «конечный цилиндр-пластины» уменьшается на 23. .. 28% в зависимости от меридионального угла установки передних дефлекторов, в то время как для бесконечного цилиндра это снижение составляет 60%. В работе рассматривается возможность применения этого метода на практике для снижения сопротивления лёгких самолётов, имеющих цилиндрические обтекаемые элементы. Алгоритм рационального выбора параметров дефлекторов и пластины для минимизации лобового сопротивления представлен в виде схемы на рис. 1.

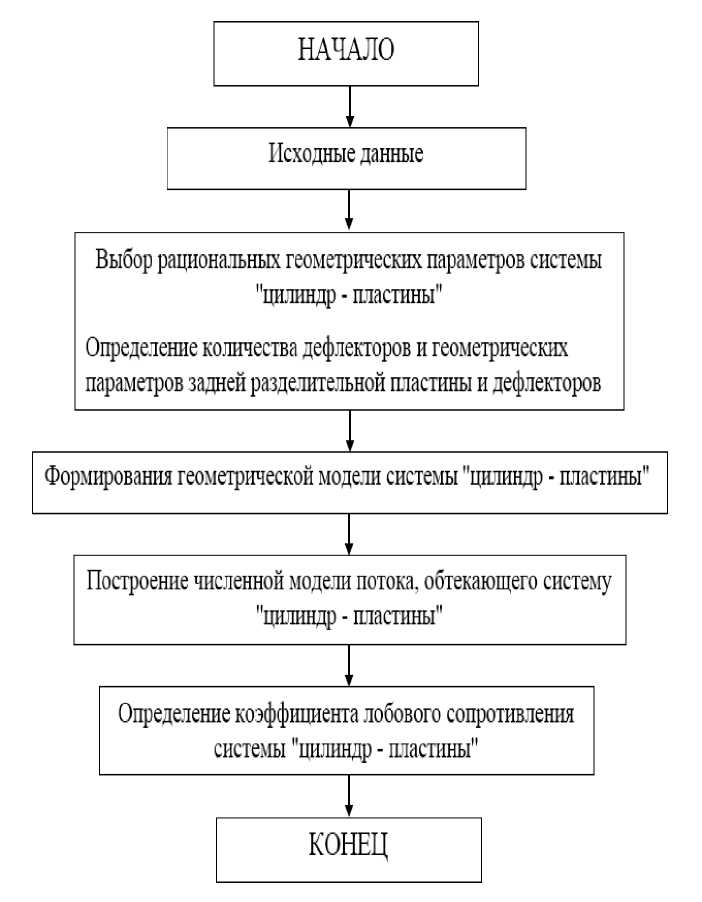
Рис. 1. Схема алгоритма метода снижения лобового сопротивления цилиндра при наличии пластин вблизи его поверхности

Описанный выше алгоритм метода снижения лобового сопротивления апробирован на примере широко распространённого лёгкого самолёта Cessna-172. Для самолётов, относящихся к лёгкому классу, аэродинамическое качество играет очень важную роль. Так как мощность их двигателя мала, то для увеличения дальности полёта самолёта либо нужно увеличить подъёмную силу, либо снизить лобовое сопротивление. Снижения лобового сопротивления можно достичь уменьшением индуктивного сопротивления, что достигается за счёт удлинения крыла. Но удлинение крыла приводит к понижению прочности конструкции, поэтому для таких самолётов часто используют подкосы крыла. Для снижения лобового сопротивления подкосов или цилиндрических стоек шасси, или любых элементов с цилиндрическим поперечным сечением на самолёте может быть использована установка системы пластин в виде дефлекторов вблизи этих элементов спереди и задней разделительной пластины сзади.

Для самолёта с неубирающимся шасси можно снизить лобовое сопротивление путём добавления дефлекторов вблизи цилиндрических стоек шасси. Конечно, полное убирание шасси - это единственный способ практически устранить сопротивление от таких элементов. Однако дополнительный вес и высокая стоимость механизма уборки шасси обычно не подходят для лёгких самолётов.

В данной работе рассматривается эффективность применения метода снижения сопротивления самолёта Cessna-172 (рис. 2), который принадлежит к самой популярной серии легких самолётов в мире. Внешний вид самолёта Cessna-172 показан на рис. 2, а в табл. 1 представлены некоторые его геометрические характеристики и указана крейсерская скорость полёта [5].

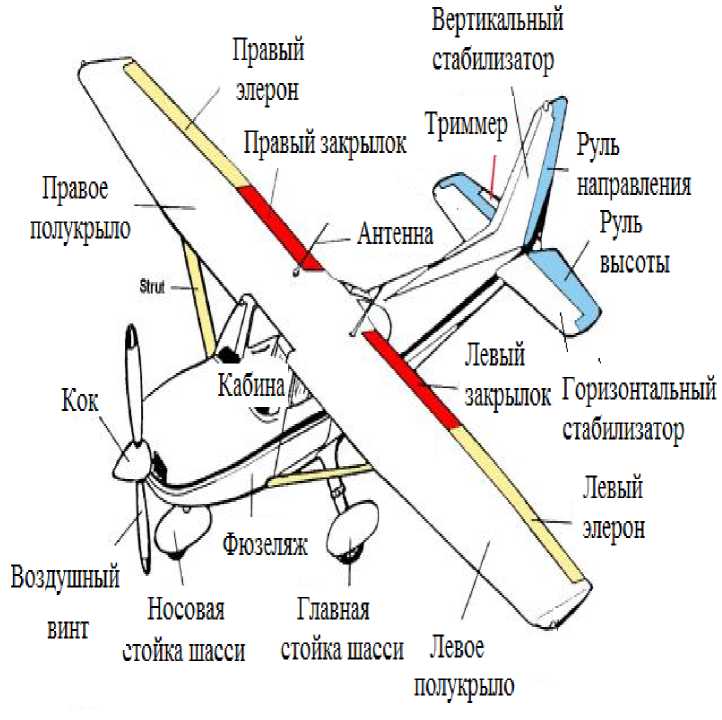
Рис. 2. Самолёт Cessna-172

В статье решается модельная задача, суть которой состоит в том, что цилиндры, которые использованы в подкосах крыла и элементах шасси заменены цилиндрами с круглым поперечным сечением. Это сделано специально, чтобы наглядно показать эффект снижения лобового сопротивления самолёта за счёт использования дефлекторов и пластины сзади цилиндров (рис. 3). Модель самолёта построена в программе Inventor и затем импортирована в программу Ansys Fluent [6].

Таблица 1

Геометрические размеры и крейсерская скорость самолёта Cessna-172 [5]

Длина самолёта	8,2 м
Размах крыла	И м
Высота	2,72 м
Площадь крыла	16,2 м2
Крейсерская скорость V	200 км/ч (54 м/с)
Толщина крыла, ГО, ВО	0,05 м
САХ крыла	1,5 м
Диаметр фюзеляжа	0,9 м
Диаметр стойки шасси	0,05 м
Диаметр колёс шасси	0,3 м
Диаметр подкосов крыла	0,05 м
Длина подкосов крыла	3 м
Длина стоек шасси	0,3 м

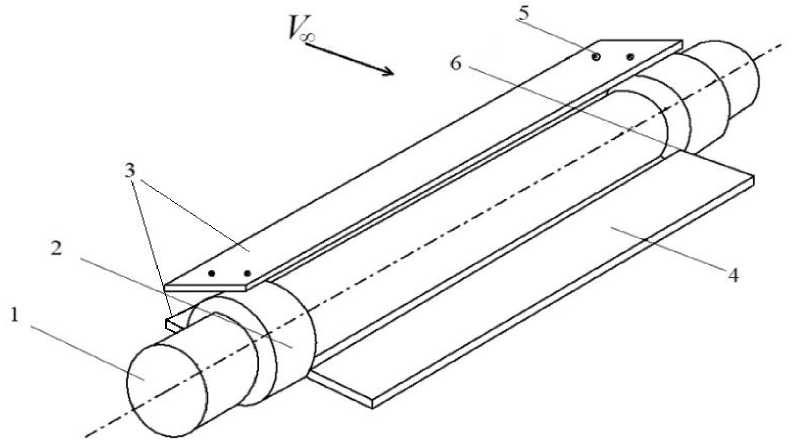
Рис. 3. Схема цилиндрического тела с системой пластин: 1 - цилиндрическое тело, 2 - муфты, 3 - передние дефлекторы, 4 - задняя пластина, 5 - крепёж дефлектора к муфте, 6 - пазы для закрепления задней пластины

1.    Постановка задачи

Рассматривается трёхмерное течение около самолёта Cessna-172. Решаются осреднён-ные по Рейнольдсу уравнения Навье Стокса (RANS) для описания турбулентных течений с применением разных моделей турбулентности [7, 8]. В данной работе применялась часто используемая модель k- w SST, которая хорошо описана в работе Ментера [7]. Система уравнений RANS [8] решалась при следующих граничных условиях и настройках: - условие прилипания на всех поверхностях цилиндра и пластин ul_wall = vl_wall = wl_wall = 0; - условия невозмущённого потока на бесконечности: u ^ U ^ ,v ^ V^,w ^ 0,р ^ р^ при Ж² + У² + Z2 ^ от.

В пакете Ansys Fluent для данной задачи использовались следующие настройки:

• •    расчётная область имела вид полуэллипсоида с размерами большой и малой полуосей, равными 30 м и 15 м, что более чем в 2,7 раза больше размаха крыла и в 16,6 раза больше диаметра фюзеляжа. Такие размеры расчётной области являются доста-

• точными для данной задачи моделирования самолёта Cessna-172, что подтверждает согласование расчётных и экспериментальных данных для самолёта Cessna-172;;

• •    типы граничных условий выбирались следующие: на входе - velocity inlet, на выходе - pressure outlet',

• •    использовались следующие некоторые настройки для расчётной сетки с использованием программного пакета ANSYS (рис. 4).

• •    выбрана расширенная функция для размера сетки «Proximity and Curvature», это функция предназначена специально для моделирования в Ansys. С помощью этой функции строилась расчётная сетка более мелкой на линии или поверхности меньшего размера и более грубой на больших поверхностях или далеко от поверхностей объекта с коэффициентом роста 1,2. При CFD-моделировании уделяется большое внимание к области вблизи поверхности объекта, поэтому расчётная сетка в этой области должна иметь необходимую гладкость.

• •    наименьший размер расчётной сетки вблизи обтекающей поверхности самолёта равен 1 мм;

• •    наибольший размер расчётной сетки равен 10 мм;

• •    устанавливается 5 структурированных слоёв вблизи поверхности самолёта.

• •    В результате получается расчётная сетка с 5x105 узла ми и 2, 2x106 элементами.

Рис. 4. Сетка и расчётная область задачи

После построения расчётной сетки выполнена проверка её качества по оценочным показателям. Важным показателем качества расчётной сетки является индекс Aspect Ratio (соотношения сторон). Чем меньше этот показатель, тем лучше расчётная сетка, что обеспечивает лучшую сходимость задачи. У созданной расчётной сетки максимальный индекс качества сетки Aspect Ratio =18,9. Максимально допустимое значение этого показателя в задачах моделирования составляет 100. Можно утверждать, что расчётная сетка вполне удовлетворяет требованиям по индексу Aspect Ratio. Кроме того, индекс Skewness (асимметрии) должен быть меньше 1, и чем меньше, тем лучше. Для разработанной расчётной сетки максимальный индекс асимметрии равен 0,94. Таким образом, расчётная сетка полностью соответствует требованиям моделирования.

Выбраны следующие параметры для решателя: ✓ компоненты скорости потока на входе равны u = V х cos a;  v = V х sin a;

• ✓    на. выходе избыточное давление равно р = 0 атм:

• ✓    на. поверхности тела. - 'wall - принято условие прилипания (по slip wall): V w_aii = 0 м с:

• ✓    тип анализа: Steady State (статический);

• ✓    свойства домена (расчётной области):

• •    тип домена: Fluid Domain,

• •    материалы для домена: Air at 25 °C;

• •    свойства материала: Continuous Fluid;

• •    характерное давление: атмосферное;

• •    сдвиг домена: Stationary;

2.    Результаты моделирования2.1.    Аэродинамические коэффициенты сил для самолёта Cessna-172

Коэффициент аэродинамических сил R вычислялся по формуле

С я =

R

2 pv^s ’

где R - аэродинамическая сила, Н; р- плотноств воздуха, кг/м³; К_ю - скороств набегающего потока, м/с; S - характерная площадв, в нашем случае это площадв крыла, S = 16, 2 м². В формуле (2), если R - сила сопротивления (Д), то Ся - коэффициент сопротивления {С_ха), а если R - подъёмная сила (УД; ^то Cr - коэффициент подъёмной силы (С_уа).

Число Рейнольдса крыла, вычисленное по хорде крыла, равно pVb =1,21 [g] • 54 [/] • 15 м у      1, 8Ы0-5[кг/(м-с)]

5-106 .

Число Рейнольдса для подкоса, рассчитанное по диаметру подкоса, равно

R&D =

pVD = 1₁21^Ц-54_Щ._0,05м у         1 , 81 - 10 ^{- 5}[кг/(м-с)]

Расчёт проведен для двух значений угла атаки: а = 0°Сиа = 5 °C. Результат моделирования показан на рис. 5 и в табл. 2.

Таблица 2

Коэффициенты аэродинамических сил для двух углов атаки

Угол атаки, а, град	Коэффициент сопротивления, Сха	Коэффициент подъёмной силы, Суа
0	0.0391	0.238
5	0,0661	0,654

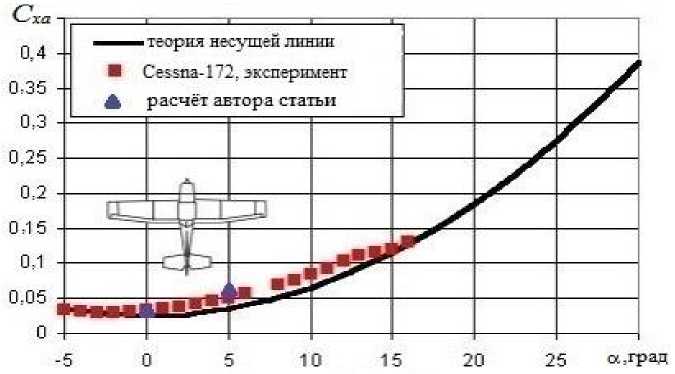
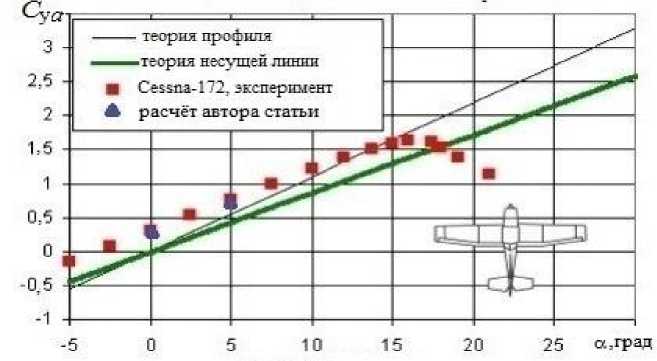
Экспериментальные характеристики самолёта Cessna-172, опубликованные в работе [5], представлены на рис. 6. В данной статье проведено сравнение полученных результатов с экспериментом не только для коэффициента лобового сопротивления, что является главной целью исследования, но и для коэффициента подъёмной силы для доказательства достоверности и точности расчёта. Несмотря на отличие в модельной задаче геометрии поперечных сечений от геометрии существующих поперечных сечений подкосов и стоек шасси самолёта Cessna-172, полученные аэродинамические коэффициенты С_ха, С_уа в данном расчёте хорошо согласуются с экспериментом [5].

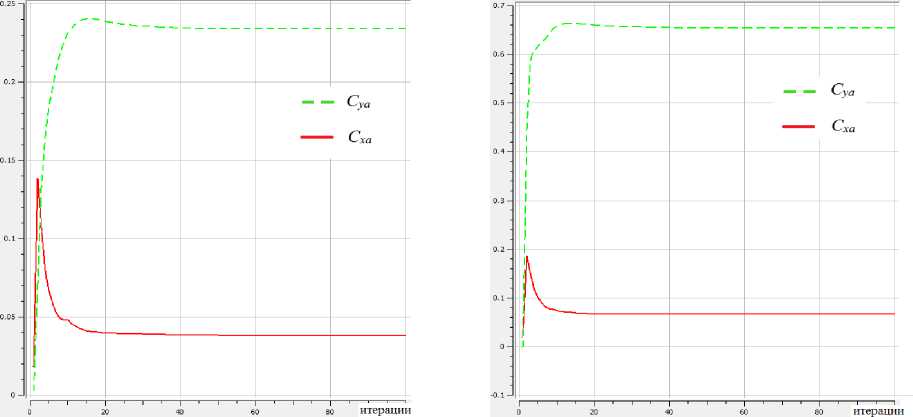
=0º                     б =5°

Рис. 5. Коэффициенты аэродинамических сил по итерациям

а)

б)

Рис. 6. Сравнение расчётных и экспериментальных данных [5] для коэффициентов лобового сопротивления а) и подъёмной силы б)

2.2.    Коэффициенты аэродинамических сил для самолёта Cessna-172 с применением дефлекторов и задней пластины

Решена модельная задача на примере применения метода снижения лобового сопротивления для самолёта Cessna-172. Модельная задача заключалась в замене всех подкосов и стоек шасси самолёта Cessna-172 на цилиндрические элементы. На подкосах и стойках шасси самолёта закреплялись пластины длиной L = 4 ■ D = 0,2 м (рис. 7) и дефлекторы с хордой 6_деф = 0,5 • D = 0,025 м, углами расположения в = ±40°, 5 = ±20°. Выбор параметров дефлекторов и задней разделительной пластины исследован в работе [2].

а) внешний вид самолёта спереди

Рис. 7. Элементы самолёта с системой

б) вид на переднюю стойку, вид снизу

«цилипдр-пластипы»

Применены такие же основные настройки для расчётной сетки и решателя, как и в предыдущем случае. Но для более детального моделирования течения в области пластин и дефлекторов при построении расчётной сетки использовалось сгущение с размером первой ячейки 0,1 мм. В результате моделирования в ANSYS Fluent получен коэффициент лобового сопротивления самолёта с системой «цилиндр-пластины»: С^акомб. = 0,0381-Относительное снижение коэффициента лобового сопротивления всего самолёта по сравнению со случаем отсутствия пластин вблизи подкосов и стоек шасси составило

0,0391

-

0,0381

0,0391

= 2,55% « 2,6%.

Такое на первый взгляд небольшое снижение коэффициента лобового сопротивления всего самолёта может при длительной эксплуатации самолёта привести к существенной экономии топлива или к увеличению дальности полёта.

Выводы

Представлены результаты моделирования в вычислительном пакете Ansys Fluent по определению аэродинамических коэффициентов самолёта Cessna-172 в двух случаях: 1) с подкосами и стойками шасси с цилиндрическими поперечными сечениями; 2) с подкосами и стойками шасси с цилиндрическими поперечными сечениями и установленными на них дефлекторами и задними пластинами. Достоверность численного моделирования доказана сравнением полученных значений этих коэффициентов с известными экспериментальными результатами, проведенными в аэродинамической трубе фирмы-изготовителя самолёта.

Подтверждён ранее обнаруженный эффект снижения сопротивления за счёт установки плоских пластин вблизи элементов цилиндрических сечений самолёта. Научная новизна работы состоит в том, что впервые показано, что у самолёта с неубирающимся шасси и длинными подкосами крыла можно общее сопротивление самолёта снизить примерно на 2,6% за счёт установки дефлекторов и задней разделительной пластины на цилиндрических элементах самолёта. Можно ожидать, что для самолётов, предназначенных для работы в сельском хозяйстве, у которых для опыления полей используются круглые трубы с длиной равной размаху крыла, эффект снижения сопротивления будет существенно сильнее. Полученный результат можно рекомендовать для использования при конструировании и проектировании не только самолётов, но и других объектов, находящихся в воздушном потоке и имеющих цилиндрические сечения.

Автор выражает благодарность своему научному руководителю к.т.н, доценту кафедры конструкции и проектирования летательных аппаратов Самарского университета Фролову Владимиру Алексеевичу за ценные советы при планировании исследования и рекомендации по оформлению статьи.