О возможности управления характеристиками многослойных виброизоляторов с конструкционным демпфированием

Проблеме рассеяния энергии в системах конструкционного демпфирования посвящен ряд работ. Наиболее полный их анализ дан в работе [1]. Одной из наиболее значимых работ этой серии является статья Гудмана и Клампа (Goodman L. Е. and Klump J. Н.) [2], в которой авторы предложили один из возможных способов расчета гистерезиса, возникающего при изгибе двухслойной консольной балки, слои которой прижаты друг к другу постоянным давлением, силой, приложенной на конце консоли. Для указанной конструктивной схемы теоретически получена математическая модель билинейной упругогистерезисной петли. Как указывают авторы работы [2], гистерезис является следствием мгновенного изменения момента инерции поперечного сечения балки в определенных точках процесса деформирования балки. При этом регулятором изменения момента инерции поперечного сечения является эпюра касательных напряжений по высоте балки. Несмотря на спорность заложенной в математическую модель [2] идеи формирования гистерезиса, авторами получены весьма достоверные данные по зависимости рассеянной энергии от амплитуды, по наличию экстремума в зависимости рассеянной энергии от контактного давления между слоями.

Аналогичные результаты получены в работе [3] для многослойной балки, сжатой постоянным

давлением. Авторами работ [3] подмечено, что в двухслойной балке проскальзывание слоев происходит мгновенно при достижении определенной сосредоточенной силы, а в многослойной — расслоения происходят сразу на каждой контактной поверхности, но по определенному закону постепенно распространяются от поверхности к поверхности.

В работе [4] на базе теории подобия и размерностей проведен широкий анализ возможностей по рассеиванию энергии различных систем конструкционного демпфирования – тросовых амортизаторов, амортизаторов из спрессованного проволочного материала, многослойных демпферов с различными эпюрами давления между слоями. Выяснено, что наилучшими демпфирующими свойствами обладают многослойные конструкции с мгновенным проскальзыванием при равномерном давлении между слоями. Этот вывод позволил разработать ряд высокоэффективных конструкций демпфирующих устройств для авиации и машиностроения.

Наиболее просто оказалось реализовать принцип равномерности сдавливающей нагрузки по длине многослойного элемента в тросовых амортизаторах [5]. Здесь упругий элемент состоит из одной или нескольких упругосвязывающих две обоймы с крепежными болтами прядей металлического троса, обмотанного с натягом проволокой.

Аналогичная идея, но для многослойного ленточного демпфера авиационного газотурбинного двигателя воплощена в конструкции, описанной в работе [6]. Равномерность сжатия слоев в пакете обеспечена с помощью специально спрофилированных упругих колец, которые служат одновременно и опорами демпфера. Экспериментальное [4] и теоретическое [7] исследование конструкций [5, 6] показало их высокую эффективность: максимальное значение коэффициента поглощения V max = W/П = = 6...7,3 (W — рассеянная циклическая энергия, а П — потенциальная энергия упругой деформации).

К сожалению, в указанных конструкциях [5, 6] максимальное значение коэффициента поглощения V max реализуется на строго определенной амплитуде и не поддается управлению в процессе развития вибраций на переходных режимах. В связи с этим у авторов возникла мысль создать конструкции амортизаторов с управляемыми характеристиками. В качестве параметра управления свойствами многослойных амортизаторов с конструкционным демпфированием выбрано давление на контактных поверхностях.

ПРИМЕРЫ КОНСТРУКТИВНЫХ

РАЗРАБОТОК ВИБРОИЗОЛЯТОРОВ С УПРАВЛЯЕМЫМИ ХАРАКТЕРИСТИКАМИ

На этом принципе разработано несколько вариантов амортизаторов [8, 10, 11]. В одном из них [8] (рис. 1) пакет упругих элементов квадратного поперечного сечения 1 охватывается хомутами 2 , внутри которых имеются прокладки 3 из электрострикционного материала, которые могут изменять свои поперечные размеры под действием электрического напряжения, подаваемого на электроды прокладок . При этом прокладки меняют давление между слоями амортизатора, изменяя и форму упругогистерезисной петли. Для раздельного управления уровнями колебаний демпфируемого объекта в двух взаимно перпендикулярных направлениях каждая из двух пар противолежащих электрострикцион-

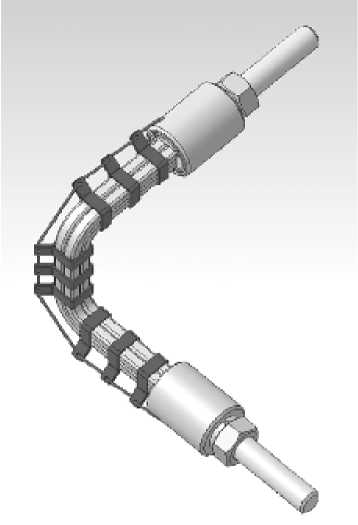
Рис. 2. Вариант управляемого виброизолятора с пространственным восприятием нагрузки [9] ных элементов связана с независимыми источниками напряжений, которые управляются сигналами от датчиков колебаний.

На рис. 2 показан вариант виброизолятора с пространственным восприятием нагрузки. Также как и в первой конструкции, под хомутами могут быть расположены электрострикционные элементы, управляемые с помощью электрических сигналов. При этом, на каждом из взаимноперпендикулярных участков виброизолятора давление на слои может осуществляться индивидуально, в зависимости от уровня вибрации в соответствующем направлении.

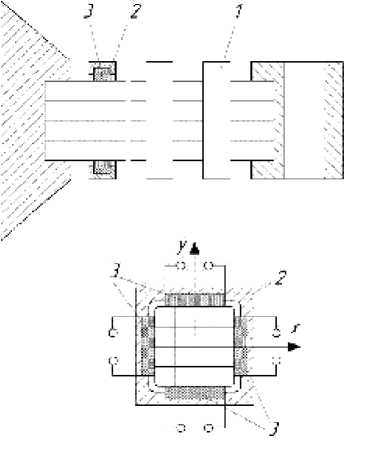
Рис. 1. Конструкция виброизолятора [8] с управляемым гистерезисом

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ МНОГОСЛОЙНОГО ВИБРОИЗОЛЯТОРА С ПОВЫШЕННЫМИ ДЕМПФИРУЮЩИМИ СВОЙСТВАМИ

Как уже указывалось ранее, демпфирующие свойства многослойных амортизаторов [8, 9] имеют высокий уровень. Однако его можно поднять еще выше. Если на контактных поверхностях пакетов (рис. 1, 2) создать пары трения с коэффициентом трения, уменьшающимся в обе стороны от нейтральной оси и подчиняющимся зависимости

3 P 1 - 4У1 2 bhnq _ n² h²

где P — амплитуда поперечной силы, при которой обеспечивается расслоение пакета, Н, у — расстояние от нейтральной оси до соответствующей контактной поверхности, мм, q —

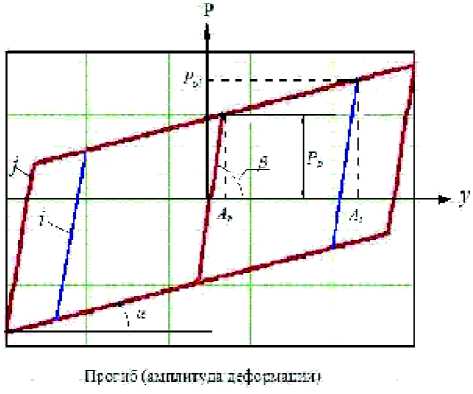
Рис. 3. Упругогистерезисная характеристика многослойного демпфера

интенсивность сдавливающей нагрузки, Н/мм2, п — число слоев в пакете вдоль данной оси, тогда при достижении уровня касательных напряжений, равного уровню распределенных сил трения q0 = f0, произойдет одновременное проскальзывание всех слоев в пакете. Петля гистерезиса при изгибе такого упругогистерезисного элемента и при постоянном давлении q будет иметь вид параллелограмма (рис. 3) с двумя характерными жесткостями: начальной (нерасслоенной), определяемой выражением uEn3 J Cо = tge = ^|^,

и расслоенной

µ EnJ c p = tg a =

где α – угол между горизонтальной осью х и участком нагрузочной кривой, соответствующий расслоенной балке; β – угол между горизонтальной осью х и участком нагрузочной кривой, соответствующий нерасслоенной балке; µ — коэффициент, зависящий от граничных условий перемещения подвижного конца балки; Е — модуль упругости лент пакета, Н/мм ² ; J=bh³/12 — момент инерции поперечного сечения одного слоя в пакете, мм ⁴ ; l — длина пролета балки, мм.

При этом коэффициент поглощения ψ определяется в виде

ψ =

16 bqhf , (1 - -) n

3 P ’

где f0 — максимальное значение коэффициента трения в паре трения на нейтральной оси пакета. Из этой формулы видно, что величиной сдавливающих нагрузок q можно управлять уровнем коэффициента поглощения ψ. Для обеспечения постоянства коэффициента поглощения ψ=ψ0=const, не зависящего от амплитуды силы Р, необходимо обеспечить закон сдавливающих нагрузок q = 3 Pv о .

16 bhf ,(1 - 1) ⁽⁵⁾

n

Поскольку амплитуда силы Р , действующей на виброизолятор, зависит от ускорений защищаемого от вибрации объекта, зависимость (5) несложно организовать с помощью простой электронной схемы с датчиком ускорений, размещенном на объекте виброзащиты.

Что касается квадратичного закона распределения коэффициента трения по толщине многослойного пакета f(x,y) с максимумом f₀ на нейтральной оси, то его можно реализовать с помощью, например, различных покрытий. Таким образом, на базе демпферов и виброизоляторов с конструкционным демпфированием можно создавать параметрически управляемые системы виброзащиты.

РАСЧЕТНОЕ ИССЛЕДОВАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

Рассмотрим возможности созданной модели параметрически управляемого виброизолятора. Определим исходные параметры системы. Имеем многослойную стальную балку высотой Н=const , состоящую из n слоев. Высота каждого слоя h , ширина b , длина l . Принимаем квадратичный закон распределения коэффициента трения по толщине многослойного пакета (балки) с максимумом f₀ на нейтральной оси (рис. 4). Пусть поверхность каждого слоя обработана таким образом, что коэффициент трения на нейтральной оси балки составляет величину, равную f₀=0,15 .

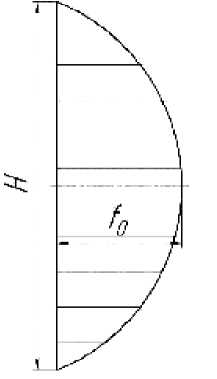
Рис. 4. График распределения значений коэффициента трения по высоте балки

Прижатие слоев балки друг к другу обеспечивается распределенной нагрузкой q . Балка нагружена на конце сосредоточенной силой P . Приняв условно величину ц = 3 , обозначим жесткост-ные параметры гистерезиса в виде

Найдем параметры, производные от гистерезиса – среднециклическую жесткость

P

С = PL

A

3E • J

C =_____ Р-.

p         13      ,

C = 3 E • Jн н l3      ,

где J_р , J_н – моменты инерции поперечного сечения расслоен ной и нерасслоенной балки соответственно.

Расслоенный момент инерции равен:

и рассеянную циклическую энергию, равную площади упругогистерезисной петли, рассчитанную при некоторой произвольной амплитуде А :

W = 4 A • P _o - 4 P p • A p - 4( P _o - P p ) • ( A + A p ) .(14)

При этом коэффициент рассеяния энергии найдется в виде:

2 W

V =---- A • Po .

J = V p t l 12

нерасслоенный –

b • h ³ = n

12 ^,

J =

н

b • H ³

3 b • h ³

---= n ---

12        12

.

Определим силу и прогиб, при которых произойдет расслоение балки:

Задавшись конкретными значениями введенных параметров и используя выражения (1)…(15), построим зависимость коэффициента рассеяния энергии от амплитуды и числа слоев балки (рис. 5):

Подставив (8) и (9) в (12), при n ^^ , легко найти предел функции (15), который оказывается равным V max = 8 при оптимальной амплитуде

P p = 3 b • H • f о • q ,          (10)

A

optim

= ap •

1 +

V

^

А С ap cp J

P • l3

A = p--- p   3 E • J_H ^.

Тогда, сила при максимальной амплитуде

отдельной петли

Данная зависимость является линейно возрастающей функцией от числа слоев (рис. 6).

Исследуем зависимость коэффициента рассеяния энергии от числа слоев при оптимальной амплитуде. Для этого представим максимальное значение силы, соответствующее оптимуму в виде

P 0

A • C_H • sign ( y ), если A <  A_p

^[( A ^{- a} p ) • C p + P p ] • sign(y), если A >  A p ^.(12)

optim max

(Aoptim — Ap ) • ^ + p k2              p ,

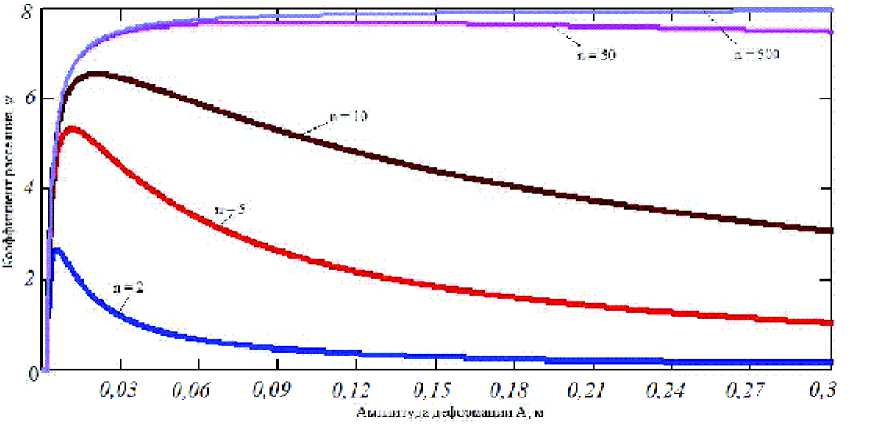
Рис. 5. Зависимость коэффициента рассеяния энергии от амплитуды деформации при фиксированном числе слоев. Здесь l = 1 м, b = 0,1 м, H = const = 0,1 м, q = 10 МПа , f₀ =0,15

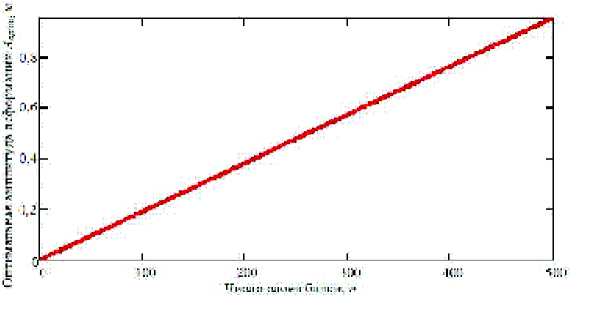
Рис. 6. График зависимости оптимальной амплитуды от числа слоев балки

а площадь гистерезисной петли на оптимуме в виде optim                optim max        optim max p p

- 4( P mPim - P p ) • ( A optm + A p ).           (18)

постоянной амплитуде A_max и числе слоев n . Для этого подставим в соответствующее выражение значение силы расслоения P_p , предварительно обозначив набор констант как Z

Тогда коэффициент рассеяния энергии на оптимуме будет представлен выражением

Z = 3 b • H • f o .           (20)

optim т max

optim

^W max

optim , optim max

Сила при данном значении прижимающей нагрузки

показанным на рис. 7.

Из рис. 7 видно, что при n >  50 , коэффициент рассеяния энергии практически постоянен в рабочей области и дальнейшее наращивание числа слоев дает незначительный прирост у . Анализируя графики, приведённые на рис. 5, 6, 7, можно увидеть, что заложенный в математическую модель принцип позволяет создать достаточно простую конструкцию, обеспечивающую практически постоянный коэффициент демпфирования на большом диапазоне частот и амплитуд работы виброизолятора, и близкий к нулю при малых амплитудах, т.е. в зарезонансной области.

Далее определим зависимость величины рассеянной энергии от сжимающей нагрузки q при

A • C „, если A <  A„ нp

P o =^

A

Ik

Zc1

СН J

• C_p + Z • q, если A >  A p •⁽²¹⁾

Зависимость площади гистерезисной петли от величины прижимающей нагрузки (рис. 8)

W = 4 A • P - 4--q qq

Cн

-

Z • q

⁴( Pq - Z • q ) • A+-^ .(22) k c h J

Исходя из формы графика, представленного на рис. 8, можно заключить, что оптимальное

значение прижимающей нагрузки равно полови не его максимального значения. Определим мак

-

симальное значение прижимающей нагрузки,

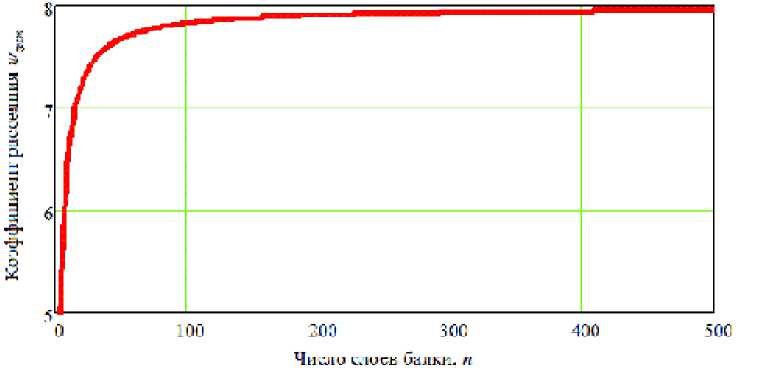
Рис. 7. График зависимости максимального коэффициента рассеяния энергии от числа слоев при оптимальном значении амплитуды деформации

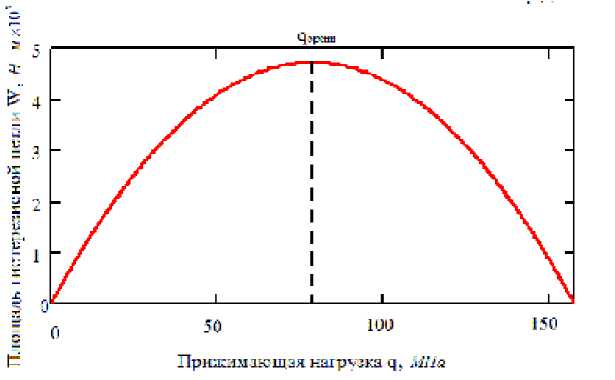
Рис. 8. График зависимости площади гистерезисной петли от величины прижимающей нагрузки (число слоев балки n=5)

для чего приравняем левую часть уравнения (22) к нулю и разрешим полученное квадратное уравнение относительно q . При этом избавимся от ветвления в значении силы P , приняв, что когда W=0 , сила вычисляется по нерасслоенной жесткости, т.к. расслоения не происходит.

Тогда максимальное значение прижимающей нагрузки, при которой расслоения на данной амплитуде А уже не происходит:

Если продифференцировать функцию Щ =f (q) по q и приравнять производную к нулю для нахождения прижимающей нагрузки в точке экстремума, где Щ максимален, получим квадратное уравнение, решая которое, найдем

q экстрем

A ^ С

н

^{1 -( з}- n 2 ) • ""Г

n

•

Г—Л1

С

V C H )

. (25)

q max

з A • E • H2

8 f о • 11

Отсюда следует, что при n=const , оптимальная прижимающая нагрузка зависит только от амплитуды и является линейно возрастающей

А оптимальная нагрузка равна половине максимальной:

функцией.

Определим зависимость коэффициента рассе-

_ 3 A • E • H2

q optim            p 33

¹⁶ f 0 • ¹

яния энергии от амплитуды и числа слоев (рис. 9)

щ ( A, n ) =

Po • A - Pp • Ap-(P, - Pp )•(A+Ap)

0,125 A • P _o

, (26)

4 5

*0,1        I-*^,P'^,,1,,!*^K

Рис. 9. График зависимости коэффициента рассеяния энергии от числа слоев и амплитуды деформации

где

P 0 ⁽ A , n ) =<

' A • C H , если A ^ A p

(A - Ap )• CH

n ²

+ P_p, если A >  A _p

При расчете системы в динамике необходимо построить амплитудно-частотную характеристику (АЧХ). Для удобства построим АЧХ в безразмерном виде. Необходимо определить коэффициент динамичности П в зависимости от относительной частоты системы. Однако для данной системы коэффициент демпфирования Y , который определяет коэффициент динамичности, зависит от амплитуды. С целью устранения этой зависимости в системе, вычислим средний коэффициент демпфирования у ср от числа слоев. Данный коэффициент не зависит от амплитуды, поэтому будем оперировать им при дальнейших расчетах динамики системы. Получим средний коэффициент рассеяния энергии

У ср

S y

A

где S _y - площадь под графиком коэффициента рассеяния энергии от амплитуды деформации, откуда средний коэффициент демпфирования

Y ep

У ср

2.п '

Функциональная зависимость коэффициента динамичности от безразмерной частоты (рис. 10), как известно, определяется выражением [12]

1 + y

^^V-^Y ) = ^(1 - V =) 2 + Y² ■      (30)

где безразмерная частота

to

V = — to0 ■

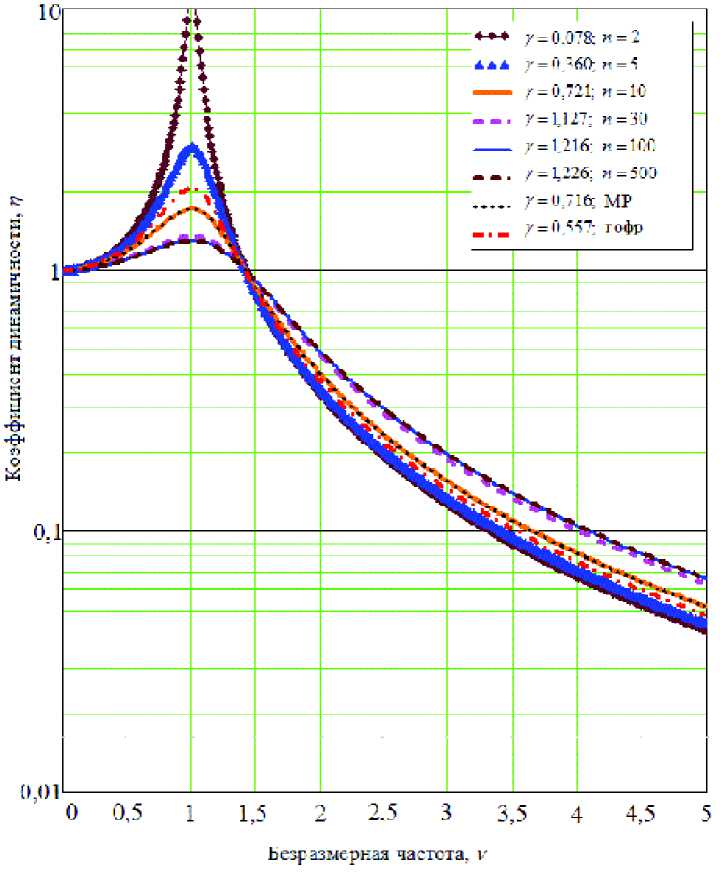
Рис. 10. График зависимости коэффициента динамичности от безразмерной частоты

а собственная круговая частота системы

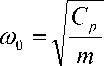
где m – масса колеблющегося груза.

Анализ графика указывает на преимущество применения в данном случае многослойных демпферов по сравнению с материалом МР или гофрированных пакетов. Так, для 100-слойной балки коэффициент динамичности равен 1,127, что соответствует приросту амплитуды на резонансе всего 30%, в то время как материал МР выдает двукратное увеличение амплитуды.

ЗАКЛЮЧЕНИЕ

Было установлено, что многослойный виброизолятор с одновременным проскальзыванием всех пластин в пакете, т. е. с реализованным в нем квадратичным законом распределения коэффициента трения по высоте многослойного пакета и равномерным распределении сдавливания слоев по ширине и длине, демонстрирует коэффициент поглощения выше, чем виброизолятор с постоянным коэффициентом трения между слоями. Кроме того, при росте количества слоев возрастает стабильность коэффициента поглощения по амплитуде деформации. В результате, уже при нескольких десятках слоев, она консолидируется вблизи теоретического предела ψmax = 8 . Причем, в пределах рабочей области ψ растет с амплитудой, обеспечивая на маленьких амплитудах минимальное, либо нулевое значение γ, что хорошо отражается на эффективности виброизоляции в области зарезонансных частот. В случае решения задачи достижения постоянства ψ по амплитуде деформации в рабочей области частот системы, её можно реализовать относительно простым линейным законом зависимос- ти интенсивности сдавливающей нагрузки q от амплитуды деформации. Это, в свою очередь, позволит обеспечить практически безрезонанс-ный переход механической системы в режим виброизоляции.