О возможности возбуждения продольной стоячей волны в цилиндрическом ограниченном капилляре, заполненном жидкостью

Как известно из теории труб малого диаметра (см., например, работу [1], с. 328), любое волновое движение внутри трубы есть движение вдоль оси трубы при условии, что периметр поперечного сечения трубы значительно меньше длины волны звука в трубе. Кроме того, в бесконечной трубе продольная фазовая скорость дискретно зависит от частоты ([1], с. 428–430). Эта зависимость определяется совокупными поперечными свойствами трубы и жидкости в ней. Другое дело — ограниченная по длине труба. В этом случае вдоль оси трубы может дискретно устанавливаться счетное количество собственных продольных колебаний, зависящих от длины трубы, от краевых условий на ее концах и не зависящих от поперечных свойств трубы и жидкости в ней. Представляет интерес строгое изучение собственных колебаний внутри ограниченной трубки на низких частотах в случае длинноволнового приближения, когда длина волны в трубе больше или сравнима с поперечным периметром трубы. Отметим, что волнами в полом цилиндре, заполненном жидкостью, занимались, например, в работах[2–4].

В работе [5] была рассмотрена задача о собственных акустических колебаниях неоднородного цилиндра, состоящего из стеклянной трубки, заполненной жидкостью. При этом вычислялись только те резонансные частоты ωm(nk) , которые обеспечивали действительные радиальные составляющие волнового вектора как в жидкости, так и в стенках капилляра. Математически это выражает- ся неравенством

( n ) kπ

®mk ^ -pm max ,                      ⁽¹⁾

где c _max = max( c 1 ,c 2 ), c , , c 2 — скорость звука в жидкости и продольная скорость звука в стенке капилляра соответственно (в [5] полагалось, что сдвиговой скоростью в стенке капилляра можно пренебречь); ^_к = П- — продольная составляющая волнового вектора, к = 1,2,..., l — длина трубки. В настоящей работе рассматриваются возможные собственные частоты, позволяющие радиальной составляющей волнового вектора быть мнимой, что означает возможность того, что горизонтальная составляющая волнового вектора превышает модуль последнего в капилляре (в рабочей жидкости и/или в стенках трубки). Такая ситуация возникает на низких частотах, т. е. в случаях, когда возможно плоское продольное движение в капилляре.

В работе изучается возможность возникновения в ограниченном по длине капилляре плоских продольных стоячих волн.

ПОСТАНОВКА ПРОБЛЕМЫ

На основе полученных в работе [5] выражений при фиксированных значениях продольной составляющей волнового вектора изучается возможность появления собственных колебаний на частотах, когда волновое движение в трубке можно считать плоским. Для этого полученная в работе [5] техника распространяется в область низких частот

( n ) kπ

^mk ^ -pm min . ⁽²⁾

РЕШЕНИЕ ЗАДАЧИ

Вначале приведем некоторые факты из работы [5], которые понадобятся для решения поставленной проблемы.

Пусть дан круговой кольцевой цилиндр, высотой l , внутренним радиусом a ₁ и внешним радиусом a , состоящий из некоторого материала плотностью ρ ₂ и скоростью продольных волн c ₂ . При этом полагаем, что сдвиговыми волнами в стенках кольцевого цилиндра можно пренебречь. Внутри кольцевого цилиндра находится основная жидкость с постоянной плотностью ρ ₁ и скоростью звука c ₁ . На границах цилиндра справедливы однородные условия Дирихле. Решение задачи на собственные колебания описанного цилиндра сводится к решению следующей задачи на собственные значения:

Решения уравнений (5), (6) с учетом граничных условий (4) равны

R - mk ( r ) = J m T 1 r ),   ^ 12 =       — I "7

c 1²⁽ r )    t 1

r e [0, a j;

^R 2 mk ⁽ r ) = ^C1 ^Jm ^T 2 r ) ^{+ C} 2 ^Nm ^T 2 r ),

σ ₂

Л   ( kn Г c 22( r)   t 1 J

r e [ a₁,a ].

Постоянные C i , i = 1,2 находятся из условий сопряжения на границе r = a 1 [5] и равны

C 1 = — х ρ ₁

R mk ( Г ) +      R mk ( Г )

d r ²           r d r

—

( 1

m ²

t +

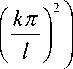
R mk ( Г ) +

4-. Rmk ( Г ) = 0, c ² ( r )

R mk (0) <» , R mk ( a ) = 0,                       (4)

которая распадается на следующую систему уравнений:

7ГR1 mk (r) + --R1 mk (r) — —R1 mk (Г) + dr2           r dr           r2

+

t c -² ( r )

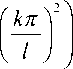
^R 1 mk ^{( r} ) = 0, ^{r e [0, a}1^] ;

.R2mk (r) + --R2mk (Г) —    R2mk (Г) + dr2           r dr           r2

+

t c 22 ( r )

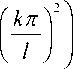
^R 2 mk ⁽ r ) = ⁰ ,    r ^{e [ a}- , ^a ]•

Искомой является система собственных значе- ( n )        ( n )

ний {Л»k)} и фУнкЦий Rmk (Kkr)• ЗДесь m = 0,±1,±2,... Собственные частоты равны

( n )

со , mk

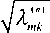
_х Р 1 ^Jm ( £ - ^a ^ ⁽ Р ~1 ^a i ) ) ' ^Nm ⁽ ^ 2 ^a i )

^Jm ( С 2 ^a 1 ) ( N m ⁽ ^ 2 ^a 1 ) ) "  ^Nm ⁽ ^ 2 ^a1) ( ^Jm ⁽ ^ 2 ^a 1 ) ) ' ’ (10)

C ₂ = — х

ρ ₁

^X P 2 ( ^Jm ^{( С} 1 ^a1 ) ) ' ^Jm ( С 2 ^a 1 ) ^— P 1 ( ^Jm ^{( c} 2 ^a 1 ) ) ' ^Jm ^{( С} 1 ^a1 )

^Jm ^{( C} 2 ^a 1 ) ( ^Nm ^{( C} 2 ^a 1 ) ) "  ^Nm ( С 2 ^a 1 ) ( ^Jm ( С 2 ^a 1 ) ) '    ^.

При поиске собственных частот в работе [5] рассматривался только случай С 1² >  0 и с т ₂ ² >  0. В нашем случае необходимо рассмотреть как положительные, так и отрицательные значения величин <т 1² и т ₂ ² . В случае, если С 1² <  0, решением уравнения (5), конечным при r = 0, является функция [6]

^R 1 mk ^{( r} ) = I — ^{( т} 1 ^r ), ^Т 1 = ^{i T} 1 , ^{r е [0, a} 1^] ;      ⁽¹¹⁾

при т ₂ ² <  0 решение уравнения (6) может быть представлено в виде

^R 2 mk ^{( r} ) = ^{a I}m ^{( т} 2 r ) ^{+ e K}m ^{( т} 2 r ),        (12)

т ₂ = iT ₂, r е [ a 1 , a ].

Здесь I_m , K_m — модифицированные функции Бесселя; α , β — соответствующие коэффициенты, позволяющие сопрягать решения задач (5), (6) согласно краевым условиям

^R 1 mk ^{( a} 1 ) = ^R 2 mk ^{( a} 1 ),

± dR1 mk   = ± dR 2 mk p dr p  dr

' ¹                 r = a 1        ' ²

Если предположить, что c 1 <  c ₂, то возможны ситуации, показанные в таблице.

Аналитические решения системы уравнений (5, 6)

Интервал по частоте	Решения уравнений (5), (6)
Ю <  ^ k c l	I m ( т 1 r ) ; C l 1 I m ( T 2 r ) + C 12 Km ( T 2 r )
^ k c l <  Ю <  ^ k c 2	J m ( ^ 1 r ) ; C 21 I m ( T 2 r ) + C 22 Km ( T 2 r )
Ю >  ^ k c 2	Jm ( ^ 1 r ) ; C 31 Jm ( ^ 2 r ) + C 32 Km ( ^ 2 r )

Очевидно, что выражение (10) определяет коэффициенты C ₃₁ и C ₃₂ в формулах в таблице. Ниже приведены оставшиеся коэффициенты:

C11 = - х ρ1

_х P l I m ^{( Т} 1 a l) ( ^Km ^{( т} 2 a l) ) ' — Р 2 ( I m ^{( T} 1 a l ) ) ' ^Km ^{( T} 2 a l)

I m ^{( T} 2 a l ) ( ^Km ^{( T} 2 a l ) ) ' — ^Km ^{( T} 2 a l ) ( I m ^{( T} 2 a l ) ) '   ’ (^

^C 12 = ^х

ρ ₁

_х P 2 ( I m ^{( T} 1 a l ) ) ' I m ^{( T} 2 a l ) — P l ( I m ^{( T} 2 a l ) ) ' I m ^{( T} 1 al) _;

I m ^{( T} 2 a l ) ( ^Km ^{( T} 2 a l ) ) ' — ^Km ^{( T} 2 a l ) ( I m ^{( T} 2 a l ) ) '  ’

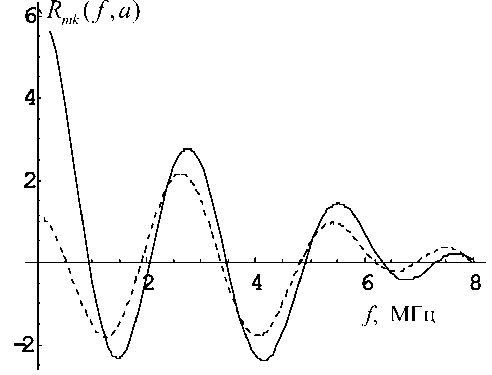
Рис. 1. Зависимость значения функции R_mk ( f , a ) в точке r = а от частоты.

m = 0 , к = 10 — штриховая линия; m = 0 , к = 50 — сплошная линия

C21 = - X

ρ ₁

_X P l ^Jm ( ^ 1 a l ) ( ^Km ^{( T} 2 a l ) ) ' — P 2 ( ^Jm ( ^ 1 a l ) ) ' ^Km ^{( T} 2 a l ) I m ^{( T} 2 a l ) ( ^Km ^{( T} 2 a l ) ) ' — ^Km ^{( T} 2 a l ) ( I m ^{( T} 2 a l ) ) '

C22 = — X

ρ ₁

_X P 2 ( ^Jm ⁽ ^ l a l ) ) ' I m ^{( T} 2 a l ) ^- P l ( I m ^{( T} 2 a l ) ) ' ^Jm ⁽ ^ l a l ) I m ^{( T} 2 a l ) ( ^Km ^{( T} 2 a l ) ) ' - ^Km ^{( T} 2 a l ) ( I m ^{( T} 2 a l ) ) '

РАЗБОР ПРИМЕРОВ

В качестве примера ниже рассмотрен реально используемый в опытах стеклянный капилляр, заполненный водой. Внутренний радиус трубки a₁ = 5 ■ 10 ^{- 4} м, внешний радиус a = 9 ■ 10 ^{- 4} м, длина трубки l = 5 ■ 10 ^{- 2} м. Плотность воды P 1 = 1, плотность стекла р ₂ = 2.5. Скорость волны в воде с₁ = 1500 м/с, скорость продольных волн в стекле принята c ₂ = 5500 м/с.

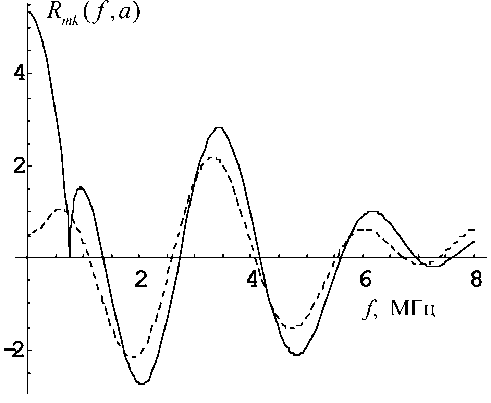
Рис. 2. Зависимость значения функции R_mk ( f , a )

в точке r = а от частоты ( m = 1 , к = 10 — штриховая линия; m = 1 , к = 50 — сплошная линия)

R mk ( f , a )

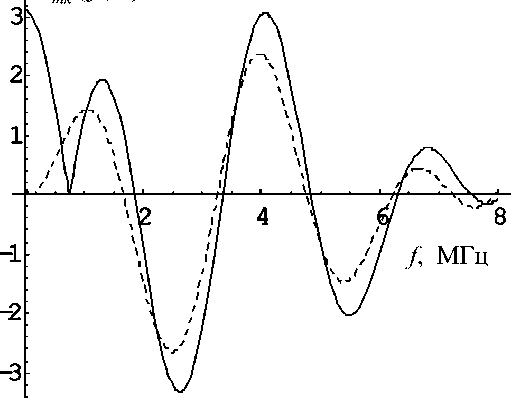
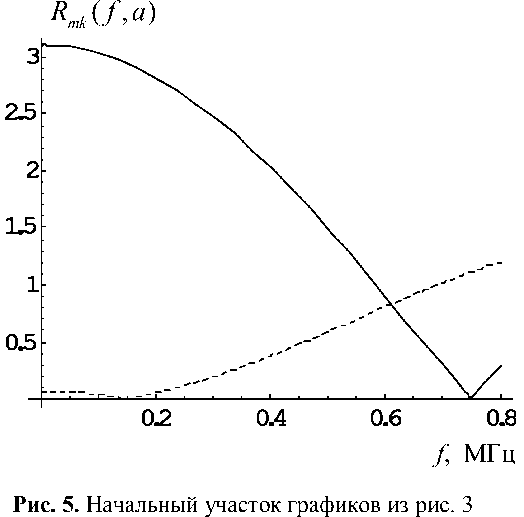
Рис. 3. Зависимость значения функции R_mk ( f , a ) в точке r = а от частоты ( m = 2 , к = 10 — штриховая линия; m = 2 , к = 50 — сплошная линия)

На рис. 1–3 представлено поведение решения (9) или (12) при r = а в зависимости от круговой частоты f для m = 0,1,2 соответственно. Частота менялась в диапазоне f е [0,8] МГц. На каждом графике представлены случаи к = 10 (штриховая линия) и к = 50 (сплошная линия). Нули этих графиков соответствуют собственным частотам. Собственные частоты для нулевой поперечной моды при to <  ^₁₀с 1 иго <  ^ ₅₀ с 1 отсутствуют (см. рис. 1). Однако на графиках для m = 1,2 (рис. 2, 3) наблюдаются нули при к 1 = ^ГО = ^_к , т. е. в случае, c ₁

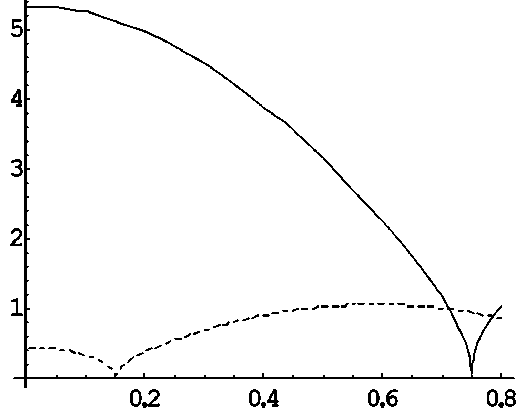
когда волновое число в жидкости в точности равно корню квадратному из соответствующего продольного собственного значения. На рис. 4–5 дана более подробная версия поведения графиков на рис. 2, 3 для m = 1,2 в окрестностях к 1 = ^ГО = ^_к , c ₁

к = 10, 50 (не путать волновое число в жидкости k ₁ и номер продольной собственной функции k ).

Нули равны в точности частотам образования продольной плоской стоячей волны с числом узлов к + 1, как если бы боковых границ трубки не существовало, в частности нули на рис. 4, 5 соответствуют f_k = ₁₀ = 150 кГц, f_k = ₅₀ = 750 кГц. Модельные исследования показывают, что при произвольном m >  0 на частотах f_k = ₁₀ = 150 кГц (для к = 10) и f_k = ₅₀ = 750 кГц (для к = 50) решения (9) или (12) при r = а равны нулю. Это означает, что f и f являются собственными частотами. к -10 к -50

f , МГц

Рис. 4. Начальный участок графиков из рис. 2

Однако, как показывают модельные решения, на этих частотах все радиальные моды при m >  0 равны тождественно нулю для r е [0, а ]. На рис. 6 для примера представлено поведение по всей толщине трубки радиальной волны первого порядка для к = 10 и к = 50, (соответственно для частот 150 кГц и 750 кГц); оба графика, естественно, сливаются в один.

Очевидно, что это справедливо для всех к = 1,2,... и m >  0, т. к. при к 1 = ^_к имеет место равенство о "1 = т 1 = 0. Отсюда следует, что решение внутри слоя жидкости равно тождественно нулю

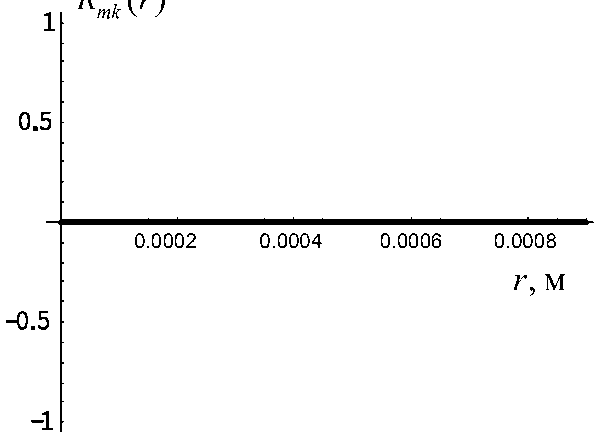
Рис. 6. Радиальные моды R_{m k} ( r ) .

m = 1 , k = 10 , f = 150 МГц;

____ m = 1 , k = 50 , f = 750 МГц

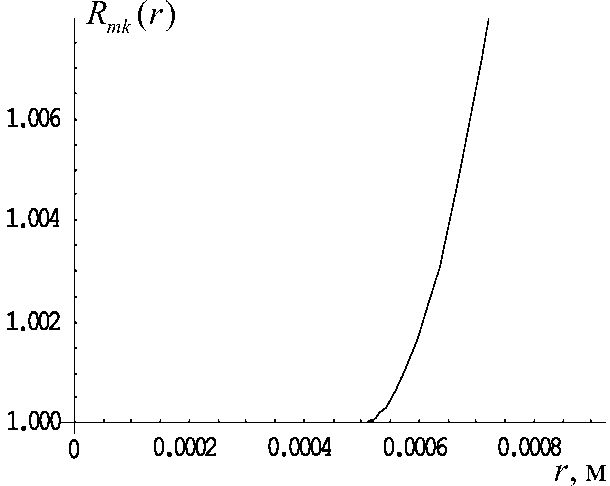
Рис. 7. Радиальная функция R_{m k} ( r ) . m = 0 , k = 10 , f = 150 МГц

при m = 1,2,..., т. к. Im(0) = Jm(0) = 0, m > 0. А из выражений (10), (14), (15) мгновенно следует тождественное равенство нулю и решений в стенках цилиндра. Отсюда следует, что собственные частоты fk = k = 1,2,... (16) 2π соответствуют тривиальным собственным функциям, равным тождественно нулю на интервале r e [0, a]. Физически это означает, что на частотах (16) не возникает никаких колебаний, иными словами плоское продольное движение внутри трубки с волновыми числами k1 = ^k невозможно. Отметим, что это относится к случаю однородных краевых условий Дирихле на внешней боковой поверхности цилиндра. Подсказка случая, когда возможны собственные колебания в виде продольной плоской волны, дается поведением решения для нулевой радиальной моды на частотах (16). Так, на рис. 7 показано распределение решения (8), (9), (11), (12) для случая m = 0, k = 10, fk=10 = 150 кГц. Из рисунка видно, что радиальное решение тождественно равно константе (единице), а в стенке цилиндра начинает возрастать. Как видно из рис. 7, граничное условие при r = а не выполняется, а это означает, что соответствующее колебание не является собственным. Оно становится таковым, только если внутренняя жидкость находится в абсолютно жестком полом цилиндре.

На рис. 8 приведено распределение нулевой поперечной моды, соответствующей всем параметрам среды, анонсированным в начале статьи,

Rmk(r)

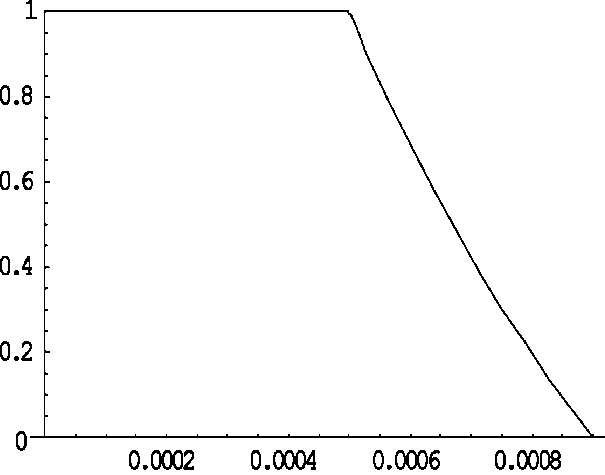
Рис. 8. Радиальная нулевая мода R m _k ( r ) , m = 0 , k = 10 , р ₂ = 2500

за исключением плотности стенки цилиндра, которая в этом случае равна р₂ = 2500 (напомним, что реальная плотность, принятая в работе, р ₂ = 2.5 ), что соответствует приближению цилиндра с абсолютно жесткими стенками (здесь m = 0 , k = 10 ). Частота резонанса нулевой моды при этом равна f = 151 кГц, что уже совсем близко к резонансу плоской стоячей волны, распространяющейся

Rmk(r)

о 0.0002     0.0004     0.0006     0.0008

r , м

Рис. 9. Радиальные моды R_{m k} ( r ) .

m = 0 , k = 10 — штриховая; m = 1 , k = 10 — сплошная; m = 2 , k = 10 — утолщенная линии;

р ₂ = 2.5

вдоль оси цилиндра f_k = ₁₀ = 150 кГц (соответствующая частота нулевой радиальной моды при р₂ = 2.5 равнялась 534 кГц). Вариация амплитуды в жидкости менее 0.035 %, что соответствует представлению о поршневой плоской волне. Как легко заметить, на высших поперечных модах m >  0 собственные колебания на частотах f_k также невозможны.

На рис. 9 для иллюстрации представлены радиальные моды собственных колебаний для k = 10: нулевой моды на частоте 534 кГц (штриховая линия), первой моды на частоте 1.1 МГц (сплошная линия) и второй моды на частоте 1.66 МГц (утолщенная линия), р ₂ = 2.5 . Как видно из рис. 9, первое не плоское собственное колебание (нулевая поперечная мода, штриховая линия) весьма удаленно соответствует представлению о продольном плоском движении. Амплитуда у стенок цилиндра примерно на 20 % меньше амплитуды на оси цилиндра.

ВЫВОДЫ

Таким образом, в работе показано, что в случае, когда стенки цилиндра не абсолютно жесткие, получение стоячих плоских продольных волн невозможно. При росте плотности стенок цилиндра хорошее приближение к поршневой стоячей волне дает собственное колебание, соответствующее первой собственной частоте нулевой радиальной моды.

Расчеты проводились с помощью пакета "Ma-thematica-7", лицензия: L3259-7547.

Автор благодарен Н.Н. Князькову и Е.Д. Макаровой за полезные дискуссии и советы, способствовавшие улучшению статьи.