О возможностью MathCAD при решения контурных уравнений электрической цепи
Автор: Тиллабоев .к
Журнал: Теория и практика современной науки @modern-j
Рубрика: Основной раздел
Статья в выпуске: 6-2 (12), 2016 года.
Бесплатный доступ
В данном статье анализируем возможности элементов теории графа и МathCAD при решении контурных уравнений электрических схем.
Электрические схемы, граф, дерево, хорды, матрица, слау
Короткий адрес: https://sciup.org/140269363
IDR: 140269363
Текст научной статьи О возможностью MathCAD при решения контурных уравнений электрической цепи
В данном статье анализируем возможности элементов теории графа и МathCAD при решении контурных уравнений электрических схем.
В работе [1] с помощью MathCAD решено узловых уравнений электрических схем. Нам известно, что узловые уравнения базировались на уравнениях первого закона Кирхгофа и закона Ома для электрической цепи. Их использования для расчёта установившегося режима электрической системы позволяет сократить порядок решаемой системы уравнений до (n-1) по сравнению с использованием системы обобщенных уравнений состояния [2], имеющей порядок m. Ещё одной возможностью снижения порядка решаемой системы уравнений является использование контурных уравнений, основанных на втором законе Кирхгофа и законе Ома. Возможность применения таких уравнений, количество которых равно числу независимых контуров (k=m-n+1), обусловлена тем, что по известным токам в хордах графа схемы замещения, число которых равно k можно однозначно определить токи в ветвях дерева графа и, тем самым -токи во всех ветвях.
Пакетные программы, с помощью которых появилась возможность решения математических задач (в том числе и других задач науки, описывающее такими же математическими моделями) без составления компьютерных программ [1,3]. В учебном процессе (иногда и в научных учреждениях) с помощью использования таких систем как MathCAD, Maple, Matlab, Mathematika и.т.д занятия становятся интереснее, осмысление содержания занятия более быстрое и глубокое а также на укрепление излагаемых понятий и на решение задач остаётся достаточно много времени. Из выше указанных систем, MathCAD - более проще чем остальные и она предназначена для технических вузов, а остальные, можно сказать, для профессиональных математиков. Именно в MathCAD задача формулируется в наиболее естественном математическом виде, а в других математических системах шаги алгоритма решения задачи записываются с помощью команд системы.
Для иллюстрации вышесказанного рассмотрим следующую
рис.1
На рис 2. данная схема показана в виде связанного направленного графа
Рис.2
Для направленного
графа, Выбрав узел d в качестве показанного рис. 2, матрица M балансирующего, получим матрицу имет вид:
M из M путем исключения
+ 1
- 1
M z
-
0 + 1
- 1
+ 1
+ 1
- 1
- 1
0 a
+ 1 + 1 b
- 1
c
узлы
0 0 d
1 2 3 4 5 6
последней строки:
|
"+ 1 |
- 1 |
0 |
0 |
- 1 |
0 |
|
|
M = |
0 |
0 |
- 1 |
0 |
+ 1 |
+ 1 |
|
-1 |
0 |
0 |
+ 1 |
0 |
- 1 |
ветви
Матрица M и N дают возможность записать уравнения состояния электрической цепи (узловых и контурных уравнений) в матричной форме.
Известно, что одной и той же электрической цепи в общем случае соответствует несколько различных систем независимых контуров, или, иными словами, одной и той же матрице M- можно поставить в соответствие несколько матриц N.
Однозначность в выделении системы независимых контуров, позволяющая получить матрицу N по матрице M, может быть достигнута при использовании таких понятий теории графов, как дерево и хорды.
Деревом называется наименьший связанной подграф, содержещий все вершины графа. Иными словами, дерево – это разомкнутая часть замкнутой схемы, которая соединяет все ее узлы. Ветви, не вошедшие в дерево схемы, называются хордами. Одна и та же схема может быть разделена на дерево и хорды по-разному. На рис.3 показаны один из вариантов разделения графа, изображенного на рис.2 на дерево и хорды.
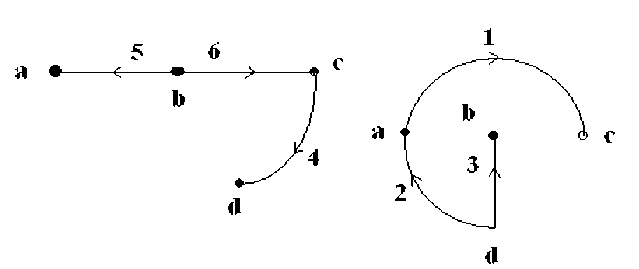
дерево
хорды рис.3
В результате матрице
M, записанная первоначального при произвольной нумерации ветвей, путем перестановки столбцов преобразуется к виду.
M = [ M a M в ]
где M - подматрица (блок), относящаяся к дереву схемы, M - подматрица, характери-зующая подграф, состоящий из хорд.
+ 1 - 10 0 - 1 0
M = 0 0 - 10 + 1 + 1
+ 1 - 1
- 1 0 0
'----------V----------2 M a
+ 1 0
-
M a
0 0
V
M e
-
- 1
- 1
M e =
0 + 1
+ 1 0
+ 1
-
Выбранный вариант дерева удобен лишь тем, что не требует перенумерации столбцов полученной ранее матрицы M .
Для определения токов в хордах I р - получается k-взаимно независимых уравнений [2]:
Z. • I k = E k - N • Z b •
Ma*
'
• J
где Zk = N • ZB • NT, I k = Ip квадратная неособенная матрица порядка k, называемая матрицей контурных сопротивлений, Ек - столбец контурных
ЭДС , J - столбец задающих токов
N = [Na Ne], Na =-MTAMaY'; Ne = 1, Zb = diag(zt) - в узлах, диоганальная
матрица сопротивлений ветвей. Решив уравнения (1) относительно I = I , можно определить токи в ветвях дерева схемы I • по (2). •
I a = M a J - M a1 M в I k (2)
Приведём алгоритм задачи:
-
• данная электрическая цепь преобразуется в виде графа
(определяются матрица M);
-
• граф разделяются на дерево и хорды;
-
• определяются матрица N -
- (N = [N. Ne], N. =-M’.W; Ne = 1 )^
-
• определяется токов в хордах I р - с помощью уравнения (1);
-
• определяется токов в дерево I - с помощью уравнения (2);
(при этом все операции над матрицами и векторами выполняется при помощью МаthCAD, система уравнения (1) и (2) решается внутренной функции Isolve.)
При исходных данных [4]: (именно эти данные берутся, чтобы сопоставить результаты) z1=12 Om, z2=11 Om, z3=10 Om, z4=10 Om, z5=z6=5
Om, E1=20, E2=25, E3=15, E4=15, E5=E6=0 (, / = 0 - при отсутствии задающих токов в узлах, что отвечает схеме замещения, в которой электростанции представлены источниками напряжения, а нагрузки -сопротивлениями) в окне МathCAD введём следующие команды и получаем результаты:
|
' 1 -1 0 0-1 0 |
'1 -1 O> |
<0-1 0) |
|||
|
M := |
0 0-101 1 |
ML := |
0 0 -1 |
MB := |
0 1 1 |
|
(-1 0 0 1 0 -lv |
. -1 0 0 „ |
J о -J |
NB
J 0 o'
0 1 0
,0 о L
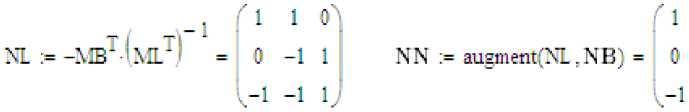
zl := 12 z2 := 11 z3 := 10 z4 ;= 10 z5 := 5 z6 := 5 el := 20 e3 := 15 e4 := 15 e5 := 0 еб = 0
1 0 1 0 0> -11010 -1 1 0 0 1, e2 := 25
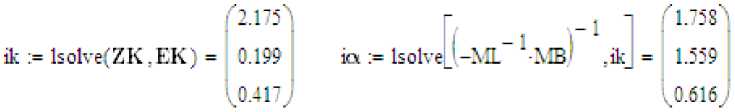
|
el |
'zl |
0 |
0 |
0 |
0 |
0 |
||||
|
e2 |
0 |
z2 |
0 |
0 |
0 |
0 |
||||
|
El := |
e3 e- |
ZB := |
0 0 |
0 0 |
Zj 0 |
0 z- |
0 0 |
0 0 |
ZK |
T := NNZBNN |
|
e5 |
0 |
0 |
0 |
0 |
z5 |
0 |
EK |
:= NN-E1 |
||
|
|
<° |
0 |
0 |
0 |
0 |
-, |
Полученные результаты совпадают с приведенными результатами [4]. (I 1 =1,78 I 2 =1,56 I 3 =0,62 I 4 =2,18 I 5 =0,22 I 6 =0,40). В заключении можно сказать что, при вычислении электрических схем, таким путём, схема преобразуется в виде графа, виделяются дерево и хорды и с помощью выше указанного алгоритма решается контурное уравнение. В этом работе особенно важный фактор является тот фактор, что без арифметических операций получаем результаты. Операции над матрицами и решения СЛАУ возложили на МathCAD.
Список литературы О возможностью MathCAD при решения контурных уравнений электрической цепи
- Тиллабоев Ё.К, Хакимов Р.М, Холмирзаев И.А. Организация приближённого решения уравнений состояния электрической цепи в МathCAD Молодой учёный. № 9, (89), май, 2015 г. стр.44-48.
- В.А.Веников и др. Математические задачи электроэнергетики. М., В.школа, 1987г.
- Охарзин.В.А. Прикладная математика в системе Mat CAD. СПб, Лань, 2008г. -352с.
- А.С.Каримов. Назарий электротехника. Т., “ЎАЖБНТ” маркази, 2003й.


