О выборе методов решения уравнения Пуассона в общем случае распределения объемной плотности заряда и о постановке краевых условий в электрокинетических задачах (обзор)
Автор: Шарфарец Борис Пинкусович, Шарфарец Е.Б.
Журнал: Научное приборостроение @nauchnoe-priborostroenie
Рубрика: Математические методы и моделирование в приборостроении
Статья в выпуске: 1 т.25, 2015 года.
Бесплатный доступ
Рассматривается распределение объемных зарядов в уравнении Пуассона, отличное от распределения Больцмана. Это потребовало привлечения аппарата корректного решения краевых задач для уравнений Лапласа и Пуассона. Использованы наиболее общие методы решения указанных задач. Рассмотрены краевые условия, применяющиеся в электрокинетических явлениях. Представлена замкнутая система связанных уравнений, позволяющих математически моделировать электрокинетические процессы в условиях отсутствия термодинамического равновесия.
Двойной электрический слой, электрокинетические явления, уравнение пуассона, уравнение лапласа, краевая задача дирихле, краевая задача неймана
Короткий адрес: https://sciup.org/14264967
IDR: 14264967 | УДК: 541.13+537.362+537.364
Текст обзорной статьи О выборе методов решения уравнения Пуассона в общем случае распределения объемной плотности заряда и о постановке краевых условий в электрокинетических задачах (обзор)
В электрокинетических явлениях важно правильно учитывать влияние основного фактора, определяющего само существование этих явлений — наличия двойного электрического слоя (ДЭС) в окрестностях границы раздела фаз. Обычно для описания электростатических характеристик ДЭС пользуются частным случаем уравнения Пуассона для электрического потенциала — уравнением Пуассона—Больцмана, решения которого как точные для ряда случаев, так и приближенные (приближение Дебая—Хюккеля) достаточно хорошо изучены. Это уравнение характеризуется некой специальной формой правой части уравнения Пуассона, т. е. специальным распределением (распределением Больцмана) зарядов в ДЭС. Такое распределение правомерно в условиях термодинамического равновесия, когда электрохимический потенциал постоянен. Термодинамическое равновесие может по каким-либо причинам нарушаться (например, вследствие наличия течения жидкости, которое вызывает возникновение потенциала течения, и т. д.). В этом случае распределение плотности зарядов может отличаться от распределения Больцмана, и тогда, если справедливо электростатическое приближение, необходимо решать уравнение Пуассона в общем виде. К счастью, теория разрешимости краевых задач для уравнений Пуассона и Лапласа хорошо изучена и описана. Авторы в работе обращаются к фундаментальной классической теории разрешимости этих краевых задач с учетом их электростатической природы. Из при- кладных соображений повышенное внимание уделяется т. н. внутренним краевым задачам, а также особенностям задания соответствующих краевых условий с точки зрения их привязки к опытно измеряемым величинам.
Ранее в работе [1] были рассмотрены некоторые аспекты решения пространственных задач для уравнений Лапласа и Пуассона, приведен ряд деталей решения краевых задач с применением теории кулонова потенциала. В настоящей работе приводятся теоремы единственности решения краевых задач, отбираются из всего разнообразия конкретные наиболее общие методы их решения. Особое внимание уделяется внутренним задачам Дирихле и Неймана и электростатическому смыслу соответствующих краевых условий вследствие того, что именно они отвечают физике электроки-нетических явлений.
ТЕОРЕМЫ ЕДИНСТВЕННОСТИ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЙ ЛАПЛАСА
И ПУАССОНА В ТРЕХМЕРНОМ СЛУЧАЕ
Рассматриваем, как и в [1], трехмерное пространство R 3 . Пусть V + — ограниченная область (связное открытое множество) V + с R 3 , S = = 5 V + — ее граница, V+ — ее замыкание и V = = R 3 \ V + — дополнение до всего пространства.
Обычно рассматривают следующие четыре краевые задачи для трехмерного уравнения Лапласа [2, с. 412]
Au = 0 .
Внутренняя задача Дирихле: найти гармоническую в области V + функцию u e C ( V + ), принимающую на S заданные (непрерывные) значения u + . (Классы комплексных функций С (•), 0 < p , определены в [2, c. 14]; при p = 0 индекс опускается).
Внешняя задача Дирихле: найти гармоническую в области V - функцию u , принимающую на S заданные (непрерывные) значения u 0 и обращающуюся в 0 на бесконечности.
Внутренняя задача Неймана: найти гармоническую в области V + функцию u , имеющую на S заданную (непрерывную) правильную нормальную производную u+ .
Внешняя задача Неймана: найти гармоническую в области V~ функцию u e C ( V ) , имеющую на S заданную (непрерывную) правильную нормальную производную u - (нормаль внутренняя) и обращающуюся в 0 на бесконечности.
Определение правильной нормальной производной дано в [2, с. 362].
Аналогичные краевые задачи ставятся и для уравнения Пуассона
Au = -f,
причем требуется, чтобы u e C 2 ( V + ) П C ( V +) для внутренних задач и u e C 2 ( V ) П C ( V ) , u ( ” ) = 0 для внешних задач.
Подстановка u = v + v, V (x ) = 1- J f(y) dy ,
V 4nV+ |x — y| сводит внутренние краевые задачи уравнения Пуассона (2) для функции u к соответствующим внутренним краевым задачам уравнения Лапласа (1) для функции v, если f e C1 (V+ ) П C (V+ ).
Для внешних краевых задач аналогично, если объемный потенциал с плотностью f существует и обращается в 0 на бесконечности.
Справедливы следующие теоремы единственности для уравнений Лапласа и Пуассона (там, где речь идет только об одной из задач, это оговаривается отдельно) [2, с. 413–415]:
Теорема 1. Решение уравнения Пуассона единственно в классе обобщенных функций, обра- щающихся в 0 на бесконечности.
Теорема 2. Решение внутренней или внешней задачи Дирихле единственно и непрерывно зависит от граничного значения u + или u 0 соответственно в указанном в [2, с. 413] смысле.
Теорема 3. Если S — достаточно гладкая поверхность, то решение внутренней задачи Неймана определено с точностью до произвольной аддитивной постоянной. Необходимым условием разрешимости этой задачи для уравнения Пуассона является равенство
J l ^ ( x ) d , +J + f ( x ) d v = 0, u +( x ) = d u dl^ SV
. (3)
x e S
В случае внутренней краевой задачи Неймана для уравнения Лапласа имеем f ( x ) ^ 0 и условие (4) преобразуется к виду (см. также [3, с. 266])
J u+( x) ds = 1^ (x) ds = 0. (4)
S S d n
Физический смысл условий (3), (4) состоит в том, что стационарный поток напряженности электрического поля через замкнутую поверхность S равен суммарной величине всех зарядов, находящихся внутри S . Далее в настоящей работе мы вернемся к физическому смыслу условия (3).
Теорема 4. Если S — достаточно гладкая поверхность, то решение внешней задачи Неймана единственно.
Следует отметить, что преобразование Кельвина [2, § 24.10] сводит внешние краевые задачи для уравнения Лапласа к внутренним и наоборот.
МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЙ ПУАССОНА И ЛАПЛАСА
В теории краевых задач для уравнений Пуассона и Лапласа обычно применяют несколько хорошо апробированных методов решения [2–4]. К ним можно отнести:
– метод разделения переменных, или метод Фурье;
– метод функций Грина;
– метод сведения краевых задач для уравнения Лапласа к интегральным уравнениям с применением теории потенциала.
Ниже подробно рассматривается применение метода функций Грина для решения задачи Дирихле и Неймана, а также смешанной краевой задачи (что понадобилось для перехода от последней к задаче Неймана) для уравнения Пуассона. Кроме того, рассматривается алгоритм решения первой (Дирихле) и второй (Неймана) задач для уравнения Лапласа методом интегральных уравнений. Оба этих метода рассматриваются потому, что решение краевых задач для уравнения Пуассона в общем случае приводит к необходимости решения соответствующих краевых задач для уравнения Лапласа. Этого удается избежать только в небольшом ряде случаев, следующих из специальных свойств симметрии области V+ (см., например, [3, с. 323–329]).
Что касается метода разделения переменных, то он достаточно подробно изложен в классических курсах по математической физике. Отметим лишь следующее: этот метод используется для задач, в которых можно редуцировать пространственную эллиптическую краевую задачу для уравнений Лапласа или Пуассона к нескольким одномерным краевым задачам, каждая из которых зависит только от одной пространственной переменной. Двумерное уравнение Лапласа разделяется в любой системе координат, получающейся конформным преобразованием из декартовой системы координат x , y . В трехмерном случае уравнения Лапласа точное применение метода Фурье возможно не только для одиннадцати известных систем координат [5, с. 614–620], позволяющих разделять трехмерное уравнение Гельмгольца, но и допускает еще целый ряд случаев, описанных в [5, с. 491–492, 621–622].
Метод функций Грина [2, 4], или метод функции источника [3]
Вначале поясним причину, по которой необходимо пользоваться методом функций Грина, а не использовать интегральные формулы Грина, выражающие решение краевых задач для уравнений Лапласа и Пуассона через значения этого решения и его нормальной производной на границе S и фундаментальное решение уравнения Лапласа [2, с. 360, 361]. Так, согласно [2, с. 361], для функций u е C ( V + ), гармонических в V+ и имеющих правильную нормальную производную на S , справедлива следующая формула Грина
( 1
u ( х ) =
4 π S x
1 d u - х01 d n
1 Г d ds 0--u — .
0 4n J дn (I x - xg| J
\
d s о . (5)
Однако из теорем единственности для задач Дирихле и Неймана для уравнения Лапласа (см. выше) следует, что, вообще говоря, не существует гармонической функции u(x) с произвольно за- дu c n данными значениями u и на S . Поэтому дn формулу Грина (5) нельзя непосредственно ис- пользовать для решения поставленных краевых задач [2, с. 415].
Такое положение устраняется в методе функций Грина, когда решение краевых задач для уравнений Лапласа и Пуассона выражается через т. н. функцию Грина, удовлетворяющую первому, второму или третьему (смешанному) краевым условиям на границе. При изложении метода будем следовать [4], где он представлен наиболее полно для всех трех краевых задач.
Будем рассматривать внутренние задачи, внешние рассматриваются аналогично. Пусть функция ф ( x , y ) гармонична в области V + по переменной y и непрерывна вместе со своими первыми производными. Тогда функцию G ( х , у )
G (х, у) = — ,—1—г + ф ( х, у)
( ,5) 4п [_|х-у| ( ,5)
называют функцией Грина [2], функцией точечного источника [3] или фундаментальным решением [4] для уравнения Лапласа в области V + .
Для функции u , непрерывной вместе со своей первой и второй производной, справедливы следующие выражения [4, с. 271] для негармонической функции u :
-J G(х, х0)Аи (у) dy + J G(х, у) ludsу -V S д n u (х), х е V+;
-f u д G ( х , y )d s у =
S д n
u
0,
( х ) , х е S ;
х е V - ,
и для гармонической u :
u ( х ) , х е V + ;
I" G ( х , у ) | u d s y - J u G ( х , y )d s y = U u (х) , х е S ;
S д n S д n 2
0, х е V - .
Задача Дирихле
Для задачи Дирихле ( f ( х ) и ^ ( х ) — непрерывные функции)
А u ( х ) = - f ( х ) , х е V + ; (7)
u (х ) = у (х), х е S полагается, что
G ( х , у ) = G d ( х , у ) = 0 при у е S . (8)
Тогда решение, выраженное через функцию
Грина задачи Дирихле GD ( x , y ) , равно
u ( x ) = J G D ( x , y ) f ( y ) d y - J ^ ( y )^ G D ( x , y )d s y ,
V S д n (9)
X G V + .
Задача Неймана
Эта задача, казалось бы, должна следовать из (11) при в ( x ) = 0 :
Au (x ) = - f (x), x g V+,
Учтем, что функция ф ( x , y ) из (6) — гармоническая, и тогда, исходя из (8), она должна быть решением граничной задачи
— = ф ( X ), X G S.
a n v h
A y ф ( x , y ) = 0, x , y g V + ,
ф(X,y) = -p^-т, X G V+, y G S.
x - y|
Смешанная задача
(краевое условие третьего рода)
Проведя те же рассуждения, что и для смешанной задачи, получаем, что решение задачи Неймана должно выражаться формулой, совпадающей с (13), если бы функция ф ( x , y ) была решением граничной задачи
A у ф ( x , y ) = 0, x , y g V + ,
В случае смешанных краевых условий краевая задача имеет вид [4]
д ф ( x , y ) d П у
-
d
dПу (|x - y| ,
X G V + , y G S .
Но такой функции не существует, т. к.
A u (x ) = - f ( X ), X G V+,
du
— + dn
в( x ) u = Pu
= ф ( X ),
X G S .
f дф д f d f 1
J дny y J дny ^Ix - y| v
d sy = 4n ^ 0,
Здесь P — дифференциальный оператор, действующий на поверхности S ,
P = — + в(x). д n v ’
Пусть функция Грина (6) для смешанной задачи G ( x , y ) = G P ( x , y ) удовлетворяет краевому условию
P y G p ( x , y ) = 0, y g S , x g V + .
Здесь оператор P y действует по переменной y .
Тогда гармоническая функция ф ( x , y ) из (6) должна удовлетворять следующей смешанной краевой задаче для уравнения Лапласа [4]
A у ф ( x , y ) = 0, x , y g V + ,
X G V+, что не согласуется с (4). Следовательно, решения задачи (14) не существует и не существует соответствующей функции Грина задачи Неймана. Однако эта трудность обходится заменой краевой задачи (14) на следующую [4, с. 279], [6, с. 241]:
A уф( X, y ) = 0, X, y G V+, дф( x, y) дПу
4 п_ д f 1 ) S д ny [ ^ - y| J
X G V + , y G S ,
S = J dsy.
S
Здесь S — площадь поверхности S . Соотношение (4) в этом случае соблюдается [4, с. 279, 280], т. е.
P y ( Ф ( X, yП P y
f 1 )
I lx - y|),
X G V + , y G S ,
-
Cf 4 п д
J ^ s +д nyV lx - y|
f 1 ))
d s y = 0,
и решение задачи (11) представляется в виде [4, с. 279]
u ( x ) = J G P ( x , y ) f ( y ) d y + J ф ( y ) G P ( x , y )d s y ,
V S (13)
X G V + .
Функция G P ( x , y ) называется функцией Грина задачи (11).
и функция ϕ существует. После ее определения функция Грина задачи Неймана GN(x, y) определяется из (6), где функция ϕ — решение краевой задачи (15), а для ее нормальной производной справедливо соотношение дGN ( X, y ) 1
.
д n y S
Окончательно решение задачи (14) выражается через функцию Грина задачи Неймана в виде [4, с. 280]
u ( x ) = J G N ( x , y ) f ( y ) d y +
V
+ J Ф ( y ) G N ( x , y )d ^ y + 1 J u ( y )d s y , x G V +.
S S S
Интеграл u ( y )d s представляет собой сред-
SS y нее значение неизвестной функции u на поверхности S , являющееся также неизвестным. Однако решения задачи Неймана, как известно, определены лишь с точностью до постоянного слагаемого, подбирая которое среднему значению решения на поверхности S можно придать любое наперед заданное значение. Следовательно, последний интеграл в (16) должен рассматриваться как произвольная постоянная.
Таким образом, найдя решение ϕ задачи (15) и определив по формуле (6) функцию Грина задачи Неймана GN ( x , y ) , можно по формуле (16) без последнего интеграла построить то из решений задачи Неймана (14) u 0 , среднее значение которого на поверхности S равно нулю
J u 0(y )d S y = 0,
S и, следовательно, u0 (x) = J GN (x, у)f (y) dy + /ф (y) GN (x, y)dsy, V S (17)
x G V + .
Все остальные решения могут быть получены добавлением к нему произвольной постоянной.
Как видно из (13) и (17), интегральное представление решения через соответствующие функции Грина в случаях смешанной задачи и задачи Неймана совершенно идентичны по форме, но различны по содержанию, как показано выше.
Таким образом, для решения внутренней краевой задачи Дирихле для уравнения Пуассона (7) необходимо предварительно решить краевую задачу Дирихле для уравнения Лапласа (10), построить с помощью этого решения функцию Грина GD ( x , y ) задачи (7) в виде (6) и получить решение исходной задачи в виде (9). Аналогично, чтобы решить внутреннюю задачу Неймана для уравнения Пуассона (14), необходимо предварительно решить краевую задачу Неймана для уравнения Лапласа (15), построить с помощью этого решения функцию Грина GN ( x , y ) задачи (14) в виде (6) и получить решение исходной задачи в виде (17).
Все остальные решения задачи (14) отличаются от (17) на произвольную постоянную. Ну и наконец, для полноты картины, чтобы решить внутреннюю смешанную задачу для уравнения Пуассона (11), необходимо предварительно решить смешанную краевую задачу для уравнения Лапласа (12), построить с помощью этого решения функцию Грина GN ( x , y ) задачи (11) в виде (6) и получить решение исходной задачи в виде (13).
Решение краевых задач Дирихле и Неймана для уравнения Лапласа методом интегральных уравнений
Выше было показано, что решение краевых задач Дирихле и Неймана для уравнения Пуассона сводится, в частности, к решению соответствующих краевых задач для уравнения Лапласа. Если исключить некоторые частные случаи, когда решение можно получить другими методами, то наиболее общим методом решения является сведение этих задач на основе теории потенциала к интегральным уравнениям Фредгольма с полярным ядром. Этот подход широко представлен в классических курсах по методам математической физики [2, 3, 7 и др.]. Далее придерживаемся текста работы [2].
Пусть S — достаточно гладкая поверхность. Тогда решение задач Дирихле для уравнения Лапласа (внутренней и внешней) ищется в виде потенциала двойного слоя [2, с. 416] (см. также относительно некоторых деталей теории потенциала приложение в [1]):
V ( 1 )( x ) = J v ( y ) cos Ф _ d. s y , x G V + , (18)
s |x - y| где v (y) — неизвестная функция; ф^ — угол между вектором y - x и нормалью n к поверхности S в точке y g S . Функция V(1) (x) — гармоническая в V+ и в V- и обладает рядом свойств непрерывности на границе S (см. [2]). Поэтому, чтобы потенциал V(1) (x) давал решение внутренней или внешней задачи Дирихле, необходимо и достаточно, чтобы соответственно были выполнены равенства
V ±( 1 ) ( x ) = и ± ( x ) , x G S ,
(1) / A где V± (x) — предельные значения потенциала V(1)( x) изнутри (V+o (x)) и извне (V_0 (x)) границы S (т. е. когда x устремляется к границе S ). Из теоремы о разрыве потенциала двойного слоя [2, с. 407] следуют интегральные уравнения для внешней задачи Дирихле:
u0 (x) = 2nv (x) + V(1) (x) = cosϕxy
= 2 nv ( x ) + j v ( У ) ।----- ;>y , x , У G S , (19)
S Iх - У и для внутренней:
u + (x ) = -2nv (x) + V(1) (x ) =
= 2nv ( x ) + j v ( y ) cos^ d s y , x , y G S . (20)
S |x - y|
После введения вещественного параметра λ и ядра
K ( x - y ) = -
2n |x - y| интегральные уравнения (19), (20) переписываются в единой форме
v ( x ) = X j K ( x , y ) v ( y ) d s y + f ( x ) , x , y g S .
S
Для внутренней задачи Дирихле X = 1
и f = - u°- , а для внешней задачи Дирихле X = - 1
2 π
u и f = ——
2 π
.
Аналогично решение задач Неймана (внутренней и внешней) ищется в виде [2. с. 416]
^'( x ) = j ^d.. x G V+ -
S x y
где ^ ( y ) — неизвестная непрерывная плотность на S . Функция V ( 0 )( x ) , гармоническая в V + и V - , обладает определенными свойствами на границе S и стремится к 0 на бесконечности [2, с. 417]. Поэтому, чтобы потенциал V ( 0 ) ( x ) давал решение внутренней или внешней задачи Неймана, необходимо выполнение равенств
= u ± ( x ) , x g S . (22)
' V < x >
V 7+
По теореме о разрыве нормальной производной потенциала простого слоя [2, с. 409] равенства (22) превращаются в интегральные уравнения Фредгольма для внешней задачи Неймана u-( x ) = -2nu (x ) + j д( y) 'os^ dsy, x, y G S, (23) S lx - y| и для внутренней задачи Неймана u+( x ) = 2nu( x) + j ^( y) cos ^xydsy, x, y G S. (24)
s |x - y|
Из равенства vxy = Tyx , x , y g S , [2, с. 406] следует, что ядро интегральных уравнений (23), (24) равно K 1 ( y , x ) = K * ( x , y ) (здесь * обозначает сопряжение ядра). После введения параметра λ интегральные уравнения (11) и (12) можно переписать единообразно [2, с. 417]
ц ( x ) = x j K * ( x , y ) ц ( y ) d s y + g ( x ) , x , y g S .
S
При этом для внутренней задачи Неймана u +
X = - 1 и g = — , а для внешней задачи Неймана 2 π
X = 1 и g = - -u^.
2 π
Имеют место [2, с. 418] следующие теоремы для разрешимости приведенных интегральных уравнений.
Теорема 5. Внутренняя задача Дирихле и внешняя задача Неймана разрешимы при любых непрерывных данных u + и u - , и их решения представляются потенциалами двойного и простого слоя соответственно.
Теорема 6 . Внутренняя задача Неймана разрешима при любой непрерывной функции u 1 + , удовлетворяющей условию ортогональности
j u1+( x )ds = 0,
S и ее решение представляется потенциалом простого слоя.
В [2, с. 426] сформулирована и теорема о разрешимости внешней задачи Дирихле, которую мы здесь воспроизводить не будем.
Таким образом, приведенные теоремы разрешимости интегральных уравнений для краевых задач уравнения Лапласа находятся в полном согласии с теоремами единственности, приведенными в начале статьи.
Отметим, что изложенных выше сведений уже достаточно, чтобы решать конкретные краевые задачи. Проделаем это на примере внутренних краевых задач Неймана и Дирихле для уравнения Пуассона. Все остальные задачи решаются аналогично.
АЛГОРИТМ РЕШЕНИЯ ВНУТРЕННЕЙ КРАЕВОЙ ЗАДАЧИ НЕЙМАНА ДЛЯ УРАВНЕНИЯ ПУАССОНА
Итак, ставится задача (14) для внутренней задачи Неймана уравнения Пуассона
Функция Грина G N ( x , y ) этой задачи имеет вид (6) (с приписыванием нижнего индекса N к G и φ ).
Для гармонической функции v n ( x , у ) ставится внутренняя краевая задача Неймана уравнения Лапласа (15)
A y V N ( x , у ) = 0, x , у g V + ;
d^N (x, у) _ 4п д f 1 _ дПу S дПу ^ |x - у|,
= u + ( x , у ) , x g V + , у g s ;
S = J d s у .
S
Отметим, что в задаче ищется решение
V N ( x , у ) , являющееся функцией переменной у , а
переменная x выступает параметром, а также то, что необходимое условие разрешимости этой задачи
I
S
d ^ N ( x , у ) д П у
d s y
—
г f 4 п д
J I S +д П у I|x — у|
f 1
d s у = 0
выполняется.
Решение задачи ищем в виде (21) потенциала простого слоя
Vn (x, у ) = V(0)( x, у ) = Jy^x-z^z, ; |у — z| x, у G V+, z G S,
шение краевой задачи для уравнения Лапласа V n ( x , у ) . Далее по (6) находится соответствующая функция Грина G N ( x , у ) , которая позволяет получить решение исходной задачи (14) с помощью выражения (17) с точностью до произвольной аддитивной постоянной (среднее значение этого решения на поверхности S равно нулю
I U 0(У)^ у = 0)
S u 0 (x) = J Gn (x, у ) f ( у ) dУ + J v( у ) Gn (x, У)ds у , VS x G V+, что и завершает решение поставленной задачи.
АЛГОРИТМ РЕШЕНИЯ ВНУТРЕННЕЙ КРАЕВОЙ ЗАДАЧИ ДИРИХЛЕ ДЛЯ УРАВНЕНИЯ ПУАССОНА
Итак, ставится задача (7) для внутренней задачи Дирихле уравнения Пуассона.
Функция Грина G D ( x , у ) этой задачи имеет вид (6) (с приписыванием нижнего индекса D к G и φ ).
Для гармонической функции v d ( x , у ) ставится внутренняя краевая задача Дирихле уравнения Лапласа (10), где
V D ( x , у ) = u о +( x , у ) .
Отметим, что в задаче (10) ищется решение V d ( x , у ) , являющееся функцией переменной у , а переменная x выступает параметром.
Решение задачи (10) ищем в виде (18) потенциала двойного слоя
где ц ( x , z ) — плотность потенциала простого слоя, зависящая от переменной z , а x — параметр, которая удовлетворяет интегральному уравнению (24)
u1+(x, у ) = 2П“(x, у ) + J m( x,z) cos^j^ ds z, s |у — z x G V+ , у, z G S.
Выражение для ядра интегрального уравнения cosψ z y2 дано в [2, с. 397, (9)]. После разрешения I у — zl этого интегрального уравнения и нахождения плотности ^( x, у) необходимо найти из (25) ре-
V d ( x , у ) = V ( 1 )( x , у ) = J v ( x , z ) ^os ^ ;^ z , s у — z| (26)
x, у G V+, z G S, где v(x, z) — плотность потенциала двойного слоя, зависящая от переменной z , а x — параметр, которая удовлетворяет интегральному уравнению (20)
u o+(x, у ) = —2nv (x, у ) + Jv (у, z) cos vy2ds z, S |у — z| x G V+, у, z G S.
Выражение для ядра интегрального уравнения cosϕ z y2 дано в [2, с. 397, (11)]. После разрешения I у — zl
этого интегрального уравнения и нахождения плотности v ( x , y ) необходимо найти из (26) решение краевой задачи для уравнения Лапласа V d ( x , У ) .
Далее по (6) находится соответствующая функция Грина G D ( x , y ) , которая позволяет получить решение исходной задачи (7) с помощью выражения (9), что и завершает решение задачи.
выражение (27) на константу εε 0 с размерностью Кл
[ е 0 ] = , после этого интегралы приобретают
В • м размерность Кл и (27) преобразуются к виду
[ ее 0 —^d s + p el ( x ) d v = 0, x g V + U S .
JS д n V +
(27а)
Размерность подынтегрального выражения в поверхностном интеграле в (27а)
ЭЛЕКТРООСМОТИЧЕСКАЯ КРАЕВАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ПУАССОНА
В теории электрокинетических явлений чаще всего рассматривают два типа граничных условий: условие Неймана и условие Дирихле (см., например, [8, 9] по условию Неймана и [10] — для условия Дирихле). Впрочем, возможны постановки иных краевых условий [11].
Условие Неймана
Вначале рассмотрим физический смысл условия Неймана при постановке краевой задачи для уравнения Пуассона. Для этого вернемся к необходимому условию разрешимости внутренней задачи Неймана для уравнения Пуассона (3). Перепишем его в следующем виде
J
S
дu (x)
—^ds + дn
J f (x)d v = 0,
V +
x g V + U S .
Согласно, например, [12–14], уравнение Пуассона для электростатического потенциала u в системе СИ имеет вид
A u = - peL .
Отсюда, сравнивая последнее уравнение и уравнение (2), получаем
f = —, εε 0
[ f ]= В/м2.
Здесь ρel — объемная плотность заряда в области V + , [ Pe l ] = Кл/м 3 ; e 0 — электрическая постоян-
Ф Кл ная, [e0 ] = — = ; e — относительная диэлек- м В • м трическая проницаемость вещества (безразмерная величина). Таким образом, размерность слагаемых
в (27) должна быть
J f (x)d v
. v +
= В • м . Умножим
au(x)! Кл . , ее0—= —y а А это означает, что функция дn м
о(x)
о ( x ) = ее 0 ^ u ^ x ) , x G S , d n
представляет собой распределение поверхностной плотности электрического заряда по поверхности S . Сами же выражения (3), (27) и (27а) описывают закон сохранения электрического заряда для электрически замкнутой области x g V + U S при условии ее совокупной электронейтральности. Следовательно, возникает следующее краевое условие для внутренней задачи Неймана
д u (x) о (x)
—^) = — , x G S . (28) д n ее 0
Сходным с (28) образом, но без привязки к необходимому условию разрешимости внутренней задачи Неймана ставится краевое условие Неймана для полупространства в [8, с. 184] и [9, с. 217] (в этом случае уравнение Пуассона становится одномерным). Отметим в обоих случаях некоторую нестрогость рассуждений при получении соответствующего краевого условия.
Очень важной в прикладном смысле является реальная оценка распределения плотности поверхностного заряда о ( x ) на границе рассматриваемой области. Подобная оценка проведена в работе [8, (9–52)] и позволяет связать величину о ( x ) с такой реально измеримой величиной, как ς -потенциал. Так, для полупространства, когда границей является плоскость y = у 2, получено следующее выражение для о ( x ) = о = const
о = + ^ 2RTee0 ^с,„ I i
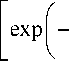
zFQ ) RT J
-1
1/2
Здесь R — универсальная газовая постоянная;
T — абсолютная температура; с , „ — концентра-
ция компонента i , моль/м3, в зоне, где потенциал равен нулю; z i — зарядовое число (валентность) компонента i ; F — число (постоянная) Фарадея; ς — дзета-потенциал; y = y 2 — плоскость скольжения.
Последнее выражение получено в предположении, что заряды распределены по закону Больцмана. Отметим, однако, что, например, для капилляра кругового или плоского сечения при условии, что радиус (толщина) капилляра много больше толщины двойного слоя, локально такой двойной слой можно рассматривать как плоский и тем самым электроосмотическое скольжение на цилиндрической (плоской) границе двойного слоя с электронейтральным объемом идентично случаю полупространства. Следовательно, последнее выражение для σ при указанном ограничении на отношение радиуса кривизны поверхности к толщине двойного слоя должно быть справедливым при распределении зарядов по Больцману и для геометрий, отмеченных выше. Подобный вывод можно обобщить и на случай более сложной формы сечения капилляра [14, с. 36].
Кроме того, при вариации объемной плотности заряда изменения происходят в диффузном слое двойного слоя, а в адсорбционном слое заряды остаются неподвижными, следовательно величина поверхностной плотности заряда на плоскости скольжения остается неизменной. То есть выражение для σ годится при тех же ограничениях и для произвольного распределения зарядов, в частности отличного от распределения Больцмана.
Толщина двойного слоя может быть порядка 10–100 ангстрем [8, с. 247].
Условие Дирихле
Пример постановки в электрокинетических задачах краевого условия Дирихле дан в работе [10, с. 809], где на поверхности S одиночной частицы граничные условия определяются заданием постоянного электрического потенциала на ней uIS =up = const .
Отметим, однако, что как бы, исходя из каких-либо соображений, ни ставились граничные условия для уравнения Пуассона для электрокинетиче-ских процессов, важно всегда помнить о разрешимости таких задач с точки зрения существования, единственности и устойчивости их решения. Что касается задач Дирихле и Неймана, то условия их разрешимости известны и приведены выше.
СВЯЗАННЫЕ СИСТЕМЫ УРАВНЕНИЙ ДЛЯ ПОЛНОГО РЕШЕНИЯ ЗАДАЧИ
Краевая задача Пуассона является важной, но не единственной в ряду задач, которые необходимо решать в нестационарных случаях электроки-нетических явлений. Здесь приведем, согласно [15], полную систему связанных задач расчета различных полей, имеющих место в этом неравновесном процессе.
Для полного решения задачи расчета всех полей, фигурирующих в электрокинетическом процессе, необходимо решить ряд связанных систем дифференциальных уравнений. В каждую систему должны входить следующие уравнения [15]:
– уравнение Навье—Стокса [15, (6)];
– уравнение материального баланса (случай без электродиффузии) [15, (30)] и при наличии электродиффузии [15, (34)];
– уравнение Пуассона [15, (4)];
– в случае наличия переменного теплового поля сюда еще необходимо добавить уравнение тепло-переноса (см., например, [16])
Решение этой системы позволяет вычислять текущую концентрацию ионов в изучаемом объеме, а значит, точно определить в нем объемную плотность электрических зарядов.
ВЫВОДЫ
Рассмотрена ситуация, когда распределение зарядов в ДЭС отличается от распределения Больцмана, что потребовало привлечения аппарата корректного решения краевых задач Лапласа и Пуассона. Выбраны наиболее общие методы решения этих задач. Были рассмотрены также краевые условия, применяющиеся в электрокинетических явлениях. Представлена замкнутая система связанных уравнений, позволяющих полностью математически моделировать электрокинетические процессы в условиях отсутствия термодинамического равновесия.
Список литературы О выборе методов решения уравнения Пуассона в общем случае распределения объемной плотности заряда и о постановке краевых условий в электрокинетических задачах (обзор)
- Князьков Н.Н., Шарфарец Б.П., Шарфарец Е.Б. Моделирование динамики двойного электрического слоя в нестационарном по времени процессе. Ч.1. О потенциале простого слоя//Научное приборостроение. 2014. Т. 24, № 4. С. 22-29.
- Владимиров В.С. Уравнения математической физики. М.: Наука, 1981. 512 с.
- Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука, 2004. 798 с.
- Кошляков Н.С., Глинер Э.Б., Смирнов М.М. Уравнения в частных производных математической физики. М.: Высшая школа, 1970. 712 с.
- Морс Ф.М., Фешбах Г. Методы теоретической физики. Т. 1. М.: Иностранная литература, 1958. 931 с.
- Араманович И.Г., Левин В.И. Уравнения математической физики. М.: Наука, 1969. 288 с.
- Владимиров В.С., Жаринов В.В. Уравнения математической физики. М.: Физматлит, 2004. 400 с.
- Ньюмен Дж. Электрохимические системы. М.: Мир, 1977. 464 с.
- Israelachvili J.N. Intermolecular and surface forces. 2nd ed. San Diego: Academic Press, 1992. 450 p.
- Гладкова Е.В., Дышловенко П.Е., Титаренко Ю.Г., Чернятьев Д.В. Упругие постоянные двумерного коллоидного кристалла в модели уравнения Пуассона-Больцмана//Изв. Самарского научного центра. 2012. Т. 4, № 3. С. 808-811.
- Perel V., Shklovskii B. Screening of a macroion by multivalent ions: A new boundary condition for the Poisson-Boltzmann equation and charge inversion//Physica A. 1999. Vol. 274. P. 446-453.
- Стрэттон Дж.А. Теория электромагнетизма. М.: Огиз, 1948. 539 с.
- Bruus H. Theoretical microfluidics. Oxford University Press, 2008. 346 p.
- Духин С.С., Дерягин Б.В. Электрофорез. М.: Наука, 1976. 332 с.
- Князьков Н.Н., Шарфарец Б.П., Шарфарец Е.Б. Базовые выражения, используемые в электрокинетических явлениях. Обзор//Научное приборостроение. 2014. Т. 24, № 4. С. 13-21.
- Шарфарец Б.П., Князьков Н.Н., Пашовкин Т.Н. О математической постановке задачи движения вязких сжимаемых теплопроводящих жидкостей в термоупругой трубке//Научное приборостроение. 2013. Т. 23, №. 4. С. 85-90.


