О выборе орбит для космических аппаратов

Продолжены исследования, начатые в [1] и посвященные решению задачи о выборе наиболее благоприятных орбит для космических аппаратов того или иного класса, а также задача распределения заданного количества спутников по заданному множеству орбит при существующих запретах на нахождение спутника на некоторых орбитах. В статье приведено решение данной задачи при следующих условиях: число спутников n совпадает с числом возможных орбит нахождения на них спутников; каждому спутнику запрещено находиться ровно на одной орбите; два спутника не могут находиться на одной орбите; количество орбит разбивается на непересекающиеся блоки определенной конфигурации ( n = p^k ). Приводится формула позволяющая вычислить число возможных комбинаций для распределений спутников по таким орбитам.

Постановка задачи, определения, обозначения

Математическая модель задачи. Под подстановкой будем понимать взаимно однозначное отображение, записанное в виде таблицы размерности 2 х n :

i ₂

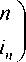
Подстановка называется регулярной, если k ^ i_k, т. е.

i 1 * 1, i 2 ^ 2, "', i n * n .

Напомним, что под порядком подстановки в теоретико-групповом смысле понимается такое минимально возможное натуральное число m, что g

m

' 1 2

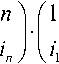
i ₂

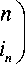
' 1   2

< i 1 i 2

n LP 2

1 = e n )

m раз

– единичная подстановка. При этом произведение подстановок – это последовательное выполнение отображений-множителей. В данной работе мы будем рассматривать случай n = p^k, где p – простое число. Будет рассмотрена задача перечисления всех регулярных подстановок степени n , имеющих порядок p . Под циклической формой записи подстановки g , степени n и имеющей порядок p будем понимать следующее:

' 1 2

к i i i 2

' n 7

=(> (') /Ок •[/ p k "') ,l ^{p k} 'H ( i ' "• i p ) "• i n - p + ' "• i n

.

Приведенные выше понятия из теории подстановок можно найти в [2]. Таким образом, каждому варианту расположения спутников на орбитах, указанному выше, будет соответствовать в точности одна регулярная подстановка вида (3). Дополнительно приведена оценка сложности вычисления числа указанных орбит.

Основные результаты

Число регулярных подстановок степени n = p ^k и имеющих порядок p будем обозначать через R ( n , p , k ) .

Теорема 1.

( p k ) ^!

^{R ( n} , p , ^{k )=}, a ■-.                                           ⁽⁴⁾

p^P • ( p k ^- ' ) !

С учетом того, что цикл при «круговом» сдвиге элементов не меняется как подстановка, имеем:

p

Число возможных комбинаций для второго цикла ( i' ²⁾. . i p ²)) равно

(pk -p)•(pk -(p + '))•.•(pk -(2p-')).

С учетом того, что цикл при «круговом» сдвиге элементов не меняется, как подстановка, имеем

p

Действуя подобным образом для последнего цикла с номером ( p^{k -} ' ) , получаем ( p k ^-( p k ^- p ) ) • ( p k ^-( p k ^- ( p ^- ' ) ) ) •.• ( p k ^-( p k ^- ( p ^- ( p ^- ' ) ) ) )

p

Произведение числа комбинаций для всех циклов есть p k • ( p k ^- ' ) •.• ( p k ^- p ⁺ ' )

p

p

(pk -(pk -p))•(pk -(pk -(p -')))•.•(pk -(pk -(p-(p -')))) p pk!

( p k ^- ' ) . p

Для завершения доказательства достаточно разделить указанную величину на р^к 1 !. Получаем

,                     p^- !

R ^{( n} , Р , ^к ) = -р-й• p ⁽ p )• p ^{- - 1} !

Теорема доказана.

Оценка сложности оптимального алгоритма для вычисления числа R ( n , p , k )

Приведём несколько полезных свойства чисел R (n, p, к), из которых наибольшую важность представляет второе из них, где приведена оценка сложности оптимального алгоритма для вычисления числа R (n, p, к).

Определение. Пусть A(n), B(n) - числовые функции, зависящие от натурального n. Выраже-х                         A(n) , ние A (n) ~B (n) означает, что lim —= 1.

v ! v !                 n ^» B (n)

Теорема 2. При n ^ да

¹            к - -1/„ п

R ( П , p , к ) ~ p ² ( Р^к / e )

.

Доказательство. Ввиду классической асимптотической формулы Стирлинга для факториала n! при n ^да : n! ~ V2пn •( n / e)"

получаем:

R ( n , p , к ) =

Р ^- !

p ⁽ Р ^{- - 1 )} • Р ^{- - 1} !

kp

,к p e

k

p ^p

Рр  ■\[2Пр

к А р-

e

k

Р г

---f n к-1 Y , к-1 p___ pi Арк e

i

Р p

р^- - ¹ а ^{р к} e )

p ^p

---( п к - 1 Y , к - 1 p

p p p

к - 1

k

Р г

^k p ^p

^{1 Г} Р‘ = p ² -

p

p i а ^{р к} e .

к - 1 Г

p

i

Р ²

Г Р

.к А ^{р к}

к e )

р - - 1 ) p e .

, 2 Г p

к - 1 А ^{р к}

e

p ^p

k

. к - 1 А ^{p - Р}

e

p ^p

^k p ^p

( и к - 1 Y

p- к e )

, к - 1

• p p p

, к - 1

Г Р - - 1 А ^Р

e

1 Р p р ^- - ¹ p ^p

i

= р ²

Г .

Р

к _А р^{- - 1} ( р - ¹ )

, к - 1

.

p ^k

• Р

Теорема доказана.

Формула (5) показывает, что число R ( n , p , k ) с ростом к растёт очень быстро, как

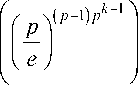
Вместе с тем В. В. Кочергин в 1994 г. в [3] привёл оптимальный алгоритм,

позволяющий находить значение 2 ⁿ (исходя из 2) за O ( log n )

арифметических операций умножения. В свою очередь Р. В. Borwein в 1985 г. в [4] привёл быстрый алгоритм для вычисления факториала n !, сложность которого равна

O ( n ( log n ( log ( log n ) ) ) 2 )

(см. также [5; 6]). Оценки сложности (6) и (7) применительно к формуле (4) для числа

R ( n , p , к ) , содержащей два факториале ( p ^k ) ! и ( p ^{k 1} ) !, дают следующий результат.

Теорема 3. Быстрые алгоритмы Кочергина и Borwein при n = p ^k и n = p ^{k 1} соответственно, порождают оптимальный алгоритм для вычисления числа R ( n , p , k ) , сложность которого

равна

O Г p ^k ■ ( log p ^k ■ log ( log p ^k ) )

Производящие функции различного типа, как и интегральные представления функций одного и нескольких комплексных переменных, являются основными инструментами современного перечислительного комбинаторного анализа [7–15]. Используя следующие хорошо известные интегральные формулы для факториала n ! и 1/ n !, например [6],

n ! = J s n e - s ds , 0

— = —— I" e^xx ^{n 1} dx , 0 <у<да , n ! 2 n L r

| x =Y

мы получаем

Теорема 4. Число R ( n , p , k ) имеет следующее интегральное представление:

R ( n , p , k )

да

J s n e s ds ■

2п1 1 r

| x =Y

e x x’ n ^{- 1} dx ,

Заключительные выкладки мы проведём с помощью метода коэффициентов Егорычева интегрального представления и вычисления комбинаторных сумм [14; 15].

Определение. Введём в рассмотрение интегралы вида да

H p ( 5 ) = J e-^{s +5} s ^p ds ,                                     (12)

где p - простое число; 8 - действительное число, не зависящее от s .

Пусть S ( z ) - производящая функция степенного типа для последовательности R ( n , p , k ) , k = 1, 2, …,

№                №              k

.

S (z ) = ZR (n, p, k) zn =ZR (n, p, k) zp k=1                     k=1

Теорема 5 (интегральное представление для функции S ( z )). Производящая функция S ( z ) допускает следующее представление:

S ( z ) = — J № e" s ⁺ tz p s p t ^-1 A ( t , k ) dsdt , ^{2 n} i\t\ = u 0

где функция (ряд) A ( t , k ) – ядро интегрального представления функции S ( z ) имеет следующий вид:

№

A (t,k )=Z( pt)

k = 1

—

■ p^{k —1} I 1

, | pt > 1 при любом p

или с учетом (12)

S ( z ) = 2 n_ J t -1 H p ( tz p ) A ( t , k ) dt .

Доказательство. Используя формулу (11) для чисел R ( n , p , k ) , имеем

№k k=1

Pk —¹ p ^p

Pk —¹ p ^p

p p ^{— 1}

№

Zzp k=1

Z z p ^—1 ) p k =1' '

№

№

p

№

№   №

Z]Z(zm) p J( sm)

k = 1 m = 0 о

e s ds •—— f e ^x x ^{1 p} dx =

2n i, r | ^x |=Y

— f e^x_x ^— 2n i । r

I ^x |=Y

^{1 — p k — 1} dx =

I ^p e ^— s

ds • — [ e ^x x "^1— p 2n i , r

| ^x |=Y

dx •§ ( m

p ^—

Здесь б ( m — p ^{k 1} ) - дельта-функция:

⁵⁽ m ^— p k ^— ) = 2П, ^J

e ^{— 1 + m — p k 1} dt , (0 <  u <№ )..

Тогда формула (16) примет вид

№

№

№

Pk —¹ p ^p

£Ш--") p-J(sp)

k = 1

1 r                1           1 r           k —1

e- s ds • —    e ^x x" ^{m — 1} dx • —    e ^{m — p}   dt

2n i, r                2n i .r

(перегруппировка членов в последней сумме с выделением в квадратных скобках тех из них, которые содержат индекс m )

Pk — ¹ p ^p

№     1     ^№   №         _

Z ]^ J J Z ( tz-s- ) • k = 1 [ ^{2 K} i t |= u 0 L m = 0

№

№

— f e ^x x" ^{m — 1} dx 2n i, r

| ^x |=Y                     ,

• e ^— s t ^{— 1 —} p k ¹ dsdt

(суммирование в квадратных скобках по индексу m , правило подстановки, замена x = tz^ps^p )

p^k — ¹ p ^p

№№

_Z _L _J J e ^zx _e- s t p k ^{— 1} dsdt = k = 1 ^{2 n} i |t |= u 0

(занесение знака суммы за знак интеграла). При этом, поскольку выбор параметра u ничем не ограничен, 0 < и < да , то мы выбираем и > 1/2, чтобы неравенство \pt\ > 1 выполнялось при любом простом p,

w

— Г - , + ,z ^p sP

²”| , |. и 0

Л w

Г1 К pt)

.- p ^{k - 1}

dsdt,

V к = 1

что завершает доказательство теоремы 5.

Заключение

Таким образом, решена задача распределения спутников по заданному множеству орбит при определенных условиях: количество всевозможных комбинаций определяется числом регулярных подстановок R ( n, p, к ) . Приведена оценка сложности оптимального алгоритма для вычисления этого числа.

Заметим, что преобразование (16) несколько парадоксально, поскольку вводит дополнительную сумму по индексу m и тем самым на порядок усложняет исходное выражение. Однако это преобразование совместно с введением дельта-функции позволило получить для числа R ( n , p , k ) интегральное представление нового типа. Отметим также, что преобразование (16) встретилось в практике метода коэффициентов впервые, что предоставляет новые возможности для эффективного применения этого метода.

В связи с вышеизложенным имеет смысл постановка следующей проблемы: изучить свойст- w ва (новой) специальной функции Hp (8) = je-s+5sPds - части ядра интегрального представле-0

ния (15) производящей функции S ( z ).