О выборе параметрической модели в задаче непараметрической идентификации

Несмотря на то, что в последнее время все большее значение приобретают цифровые управляющие устройства, до сих пор управление многими технологическим процессами осуществляется посредством или при помощи параметрических аналоговых регуляторов различных типов. Поэтому задача настройки параметров таких регуляторов не теряет своей актуальности. Ежегодно разрабатываются различные методики, рекомендации и инструкции по выбору управляющего устройства и настройке его параметров, которая может быть произведена согласно критериям устойчивости А. Гурвица (1895 г.) и А. В. Михайлова [1] при наличии явного вида передаточных функций объекта и корректирующих звеньев. При этом предполагается знание передаточной функции объекта управления или, по меньшей мере, возможность получения его переходной характеристики. В тех случаях, когда структура объекта управления неизвестна, настройка параметров производится эмпирически, что представляет определенную сложность, требует временных и финансовых затрат, а в ряде случаев и вовсе нежелательна. Знание явного вида передаточной функции объекта позволяет довольно просто и качественно настраивать параметры регулятора не на самой системе управления, а на ее модели [2].

В данной работе рассматривается метод, позволяющий получить передаточную функцию объекта управления в условиях непараметрической неопределенности при любом задающем воздействии (не требует возможности снятия переходной характеристики). Идея метода заключается в построении модели объекта путем предварительного определения порядка дифференциального уравнения замкнутой системы методами непараметрического моделирования.

Постановка задачи. Имеется замкнутая линейная динамическая система (ЛДС), корректирующим устройством которой является параметрический регулятор: пропорциональный (П-типа), пропорциональноинтегральный (ПИ-типа) или пропорционально-интегро-дифференциальный (ПИД-типа), структура которого известна, а значения параметров устанавливаются проектировщиком или иным лицом, контролирующим работоспособность системы. Сведения о структуре объекта управления отсутствуют, известны только некоторые качественные свойства: стационарный, линейный динамический объект, на вход которого поступает управляющее воздействие, выработанное параметрическим регулятором (уровень непараметрической неопределенности). Датчики фиксируют значения сигнала x*(t) (задающее воздействие), поступающего на замкнутую систему (макрообъект), и реакцию системы x(t) на задающее воздействие (рис. 1). Измерения производятся в моменты времени t(i). В каналах измерения действует центрированная помеха с ограниченной дисперсией, сведения о законе распределения помех отсутствуют. Данные измерений формируют обучающую выборку {x*(i), x(i)}, i = 1, n, некоторого объема n.

Ставится задача получения явного вида передаточной функции объекта управления, которая сводится, в свою очередь, к задаче построения математической модели замкнутого контура в случае малой априорной информации. Существуют различные методы, решающие эту задачу [3; 4], однако сам процесс моделирования зачастую достаточно трудоемкий (в основном за счет сложности выбора структуры модели) и требует больших затрат. Задача моделирования усложняется еще и тем, что измерению поддаются только задающее воздействие и выходной сигнал макрообъекта, и нет возможности измерить то управление, которое подается на сам объект. В связи с последним обстоятельством предлагается первоначально получить параметрическую модель замкнутой системы, а затем по ней определить передаточную функцию объекта управления.

Задача построения модели замкнутой системы представляет неменьшую сложность. При отсутствии каких-либо сведений о структуре объекта управления построение параметрической модели весьма проблематично. При включении корректирующего устройства и замыкании отрицательной обратной связью структура исследуемой системы становится сложнее структуры объекта управления, что, в свою очередь, увеличивает число определяемых параметров, а значит и сложность параметрического моделирования.

Структура и параметры неизвестны

Структура и параметры неизвестны

Рис. 1. Схема замкнутой динамической системы как макрообъекта

В настоящей работе рассматривается подход, позволяющий избежать сложности подбора динамической структуры посредством сочетания непараметрических и параметрических методов математического моделирования [5]. Идея заключается в предварительном определении порядка дифференциального уравнения, описывающего объект, и последующем использовании полученной информации в создании параметрической модели. Порядок уравнения предлагается определять путем построения регрессионной непараметрической модели между входными и выходными сигналами объекта, после чего задача моделирования сводится к определению значений параметров параметрической модели известными методами, например, методом наименьших квадратов.

Структурный синтез модели замкнутой ЛДС. Первая часть предлагаемого метода основана на определении порядка дифференциального уравнения, описывающего макрообъект при помощи методов непараметрической аппроксимации стохастической зависимости входного (в общем случае входных) и выходного (выходных) сигналов. По данным обучающей выборки { x * ( i ), x ( i ) } , i = 1, n , строится многомерная непараметрическая оценка регрессии Нада-рая–Ватсона [6; 7]:

где в качестве аргументов используется как входное воздействие на текущем шаге, так и значения входного и выходного сигналов на предыдущих шагах. Такой подход позволяет учитывать динамику объекта, так как значения выходного сигнала объекта на нескольких шагах, являясь аргументами оценки регрессии (1) на последующих шагах, влияют на оценку выхода.

Число s предыдущих выходных ( r входных) сигналов (которые выступают в оценке (1) в качестве аргументов), включаемых в модель, является аналогом порядка дифференциального уравнения: чем выше порядок, тем длиннее период функционирования объекта, влияющий на его последующее поведение, и тем больше данных, полученных на предыдущих шагах, мы должны учитывать.

Функция Ф( - ) - ядро (колоколообразная, дельтообразная функция) – удовлетворяет некоторым условиям сходимости [6; 7], влияние же вида ядра на точность оценивания незначительно. В данной работе использовалось параболическое ядро [8]:

[ 0,75 • (1 - z ) 2 , | z | <  1,

Ф ( z ) =

[ 0, Н ^ 1.

Параметры

J x x*(t ) - x*(i ) )

E x-ф    ,     |-ПФ| i =1         l      hx•       J j=1 1

x (t - j ) - x ( t ( i ) - j ) )

_                 x

h x (t -j )

h = ( h. , h.     , h. , I, j = 1, 5 , k = 1, r

\ x ’ x ( t - j )’ x ( t - k ))’ ^J ’ ’           ’

r

хПФ k=1 I x(t) =

Еф|

i =1

x * ( t - k ) - x*(t (i ) - k )

_________ ^hx '( t - k ) _________J___________________________ (1) x*(t ) - x*(i) \ПФ x ( t - j ) - x ( t ( i ) - j ) ,

h x

j =1

h x (t -j)

r х П Ф k =1

' x *( t - k ) - x(t ( i ) - k ) h x '( t - k )

в формуле (1) – коэффициенты размытости, настройка которых производится согласно условию минимума среднеквадратичного критерия методом скользящего экзамена. Заметим, что с ростом h сглаживающие свойства оценки нарастают, по h для каждого конечного объема выборки существует некоторый оптимум (при малых h оценка представляет собой набор непе-ресекающихся или слабопересекающихся дельтообразных функций и теряет свой смысл, а при больших h оценка становится сильно сглаженной и не отражает индивидуальных особенностей оцениваемой зависимости) [9].

Настройка значений коэффициентов размытости в формуле (1) осуществляется одним из методов оптимизации путем минимизации среднеквадратичного критерия:

1 ⁿ

W ( с ) = ⋅ ∑ ( x ( i ) - x ˆ( t , u , x ( t - j ), с ))² → min. (4) n i =1 ^с

В настоящей работе использовался метод случайного спуска, где в качестве алгоритма поиска локального минимума был выбран последовательный симплексный метод [10].

Последовательно строятся непараметрические модели (1), включающие все большее и большее число аргументов. Модель, значение критерия (4) для которой оказывается минимальным, считается наилучшей, а число предыдущих измерений выходного s и входного r сигналов, включенных в эту модель, определяют структуру параметрической модели. Работоспособность описанного алгоритма уже проверялась ранее [5]. В настоящей работе рассмотрим влияние таких факторов, как частота дискретных измерений входного и выходного сигналов и величина помехи на точность определения порядка.

Первоначально разберем вопрос о влиянии шага дискретизации на процесс моделирования. Рассмотрим незашумленную выборку. Объект управления описывался дифференциальным уравнением второго порядка, в качестве управляющего устройства использовался ПИ-регулятор. В этом случае дифференциальное уравнение, описывающее поведение замкнутой системы управления, имело третий порядок. Графические результаты работы непараметрического

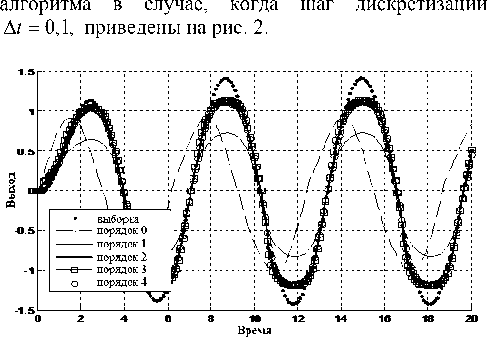
Рис. 2. Результаты непараметрического моделирования

В случае отсутствия, помехи при включении в модель двух предыдущих шагов происходит резкое улучшение качества модели (назовем этот эффект переломным моментом), которое, тем не менее, начинает незначительно ухудшаться с дальнейшим увеличением порядка (численные значения критерия (2) при разном значении Δ t представлены в табл. 1).

Из данных табл. 1 можно увидеть, что в случае чрезмерно малого значения Δ t непараметрический алгоритм имеет тенденцию к занижению порядка. При увеличении Δ t до определенного значения сначала наблюдается точность в определении порядка.

При чрезмерно большом значении Δ t динамика прослеживается хуже, что приводит к снижению точности оптимизационной процедуры настройки параметров моделей, а это, в свою очередь, влияет на точность определения порядка дифференциального уравнения. Малая представительность выборки приводит к тому, что число измерений становится недостаточным для оптимальной настройки параметров моделей, и переломный момент пропадает. Наблюдается тенденция «мнимого» улучшения качества непараметрических моделей за счет введения дополнительных членов, а следовательно, завышение порядка.

Далее проведем исследование влияния уровня помехи на точность определения порядка. Для чистоты эксперимента используем шаг дискретизации Δ t = 0,4, при котором, как было установлено ранее, для рассматриваемой системы порядок определяется правильно. По выборочным данным было проведено непараметрическое исследование путем построения моделей (1), графические результаты которого в случае 10%-й помехи приведены на рис. 3, а численные значения критерия представлены в табл. 2.

Примечание. Помеха накладывалась следующим образом: измерялся интервал изменения сигнальной части Δ, задавался уровень помех ρ (от 0 до 1). С помощью генератора случайных чисел формировался вектор (размерность вектора совпадала с объемом выборки) значений равномерно распределенной на интервале [–Δρ; Δρ] случайной величины, который впоследствии складывался с вектором значений сигнальной части.

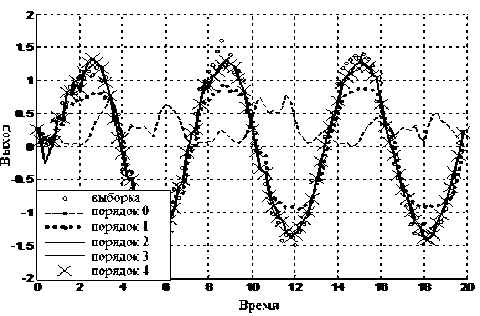
Рис. 3. Результаты непараметрического моделирования

В случае нулевой помехи (см. рис. 2) при включении в модель двух предыдущих шагов происходит резкое улучшение качества модели (назовем этот эффект переломным моментом), минимум же критерия достигается при включении в модель трех предыдущих шагов. Увеличение помехи приводит сначала к тому, что пропадает «очевидность» выбора структуры, а затем к завышению порядка, которое тем больше, чем выше уровень помехи. Отметим, что при этом пропадает переломный момент, наблюдаемый при небольших помехах: значение критерия достаточно равномерно уменьшается с добавлением в модель все большего числа предыдущих шагов. Таким образом, в качестве вывода отметим общую тенденцию к завышению порядка при больших помехах.

Таблица 1

Зависимость среднеквадратичной ошибки моделирования от шага дискретизации

Шаг дискретизации измерений	Число измерений выхода в модели
	0	1	2	3	4
0,1	0,5560	0,1352	0,0129	0,0158	0,0166
0,2	0,9889	0,1404	0,0250	0,0171	0,0244
0,4	1,1575	0,1451	0,0301	0,0174	0,0290
0,5	1,2870	0,4270	0,2202	0,1975	0,2266
1	1,0954	0,5676	0,4871	0,4019	0,2506
2	0,9265	0,8976	0,7481	0,5797	0,3915

Таблица 2

Зависимость среднеквадратичной ошибки моделирования от уровня помехи

Уровень помехи, %	Число измерений выхода в модели
	0	1	2	3	4
0	1,1575	0,1451	0,0301	0,0174	0,0290
5	1,1535	0,1283	0,0502	0,0373	0,0438
10	1,1759	0,1559	0,0651	0,0530	0,0705
20	1,1690	0,1923	0,0853	0,0573	0,0779
30	1,2662	0,2120	0,1256	0,1127	0,1142
40	1,3112	0,2706	0,1983	0,1789	0,1834
50	1,4257	0,4531	0,3861	0,3724	0,3649
100	1,5020	0,9355	0,9206	0,8883	0,8461

Рассматриваемый непараметрический алгоритм структурного синтеза модели имеет тенденцию к завышению порядка при увеличении помехи и шага дискретизации и тенденцию к занижению порядка при слишком маленьком шаге дискретизации. Тем не менее, следует отметить, что завышение порядка модели происходит при плохом качестве выборочных данных – очень высокий уровень помехи или малая представительность выборочных данных, тогда как занижение порядка происходит вследствие неверного выбора A t даже при качественной выборке (достаточный объем, низкий уровень помехи). В ряде случаев неточности определения порядка могут быть устранены на этапе параметрического синтеза за счет исключения из модели тех составляющих, для соответствующих коэффициентов которых подтверждается гипотеза равенства нулю (при завышении порядка). Однако при заниженном порядке проверка указанной гипотезы не приведет к уточнению структуры. В данной работе нас интересует не столько сама модель, сколько то, как ошибки в структурном синтезе модели могут повлиять на настройку параметров регулятора, а следовательно, на качество управления.

Получение передаточной функции объекта. Так как структура модели определена ранее методами непараметрического моделирования, задача сводится к нахождению оценок неизвестных параметров модели макрообъекта. Представим структуру модели в виде разностного уравнения [4]. Применяя метод наименьших квадратов (в работе рассматривался наиболее простой случай некоррелированных равноточных измерений), получим уравнение для вектора оптимальных оценок параметров модели [4]. В качестве характеристики точности параметрической модели регрессии использовалось так называемое значение R2 [3]. Проверка значимости коэффициентов осуществлялась на основании t-критерия [3] при уровне значи- мости а = 0,05. Результаты параметрического моделирования представлены на рис. 4.

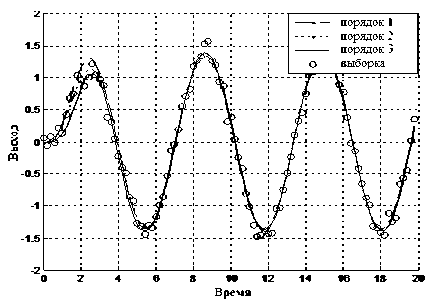
Рис. 4. Результаты параметрической идентификации моделей

На основании полученной параметрической модели замкнутой системы управления при известной модели управляющего устройства можно получить модель объекта управления.

Пример. Получение передаточной функции объек- та управления по уравнению замкнутого контура. Пусть получена модель макрообъекта в следующем виде:

MO d x MO a 4 ' "d F ⁺ a 3

d x   _MO d x   _MO

—7- + a  —7- + a dt3     2    dt2     1

+ a MO

■ x = b MO . du + b MO . _u .

¹ dt ⁰

dx

— + dt

Применяя преобразование Лапласа, получим передаточную функцию замкнутой системы

MO MO

W ( P ) =   n 1 p n °, nn . (4)

• ³      a ₄ p ⁴ + a ₃ p ³ + a MO p ² + a M p + a °

Разомкнутая система представляет собой последовательное соединение объекта управления и регулятора [11], а следовательно, передаточная функция разомкнутой системы имеет вид (в соответствии с правилом преобразования цепей)

W pJ P ) = W 0bj (P ) ■ W пи ( P ).           (5)

Используя правило Мейсона для замкнутого контура с единичной отрицательной обратной связью [11]

W ₃( P ) = " P- ' P )/1 + " P- ' P )

и учитывая тот факт, что в качестве управляющего устройства используется ПИ-регулятор, передаточная функция которого имеет вид [2; 11]

^W ПИ⁽ P ) = ^K 1 P ⁺ K 2/ P ,             ⁽⁷⁾

получаем

MO MO

W (P) =          b P „b= з      a4MO p+ a3MO p+ a2MO p 2 + a MO p + a0MO

4            3            2            1           0           ₍₈₎

_b i K 1 P ⁺ b 0 K 2

a 3 p4 + a 2 p3 + a1 p2 + (a 0 + b1 K1) p + b0 K 2 ’ где a =[a0, a1, a2, a3], b0 - коэффициенты объекта управления.

Таким образом, передаточная функция объекта управления имеет вид

W obj ( P ) =

b ₀

.

a 3 p + a 2 p + a 1 p + a 0

Зная передаточную функцию объекта управления, можно получить значения параметров конкретного типа регулятора исходя из требования устойчивости замкнутой системы [2; 11]. Таким образом, получение адекватной модели объекта как минимум позволяет избежать проблем, связанных с «выпадением» системы управления из области устойчивости, и как максимум обеспечивает возможность выбора таких значений параметров регулятора, которые бы обеспечивали желаемый результат управления.

Влияние выбора структуры на настройку регулятора. Возникает закономерный вопрос, как влияют установленные ранее тенденции завышения или занижения порядка при непараметрическом структурном синтезе модели замкнутой системы на применимость получаемой при этом модели объекта управления к настройке параметров регулятора.

Для того чтобы исследовать это влияние, по построенным ранее параметрическим моделям замкнутой системы (см. рис. 4) определим передаточные функции вида (9) соответствующих моделей объекта управления (см. пример) и рассмотрим, как согласуется настройка параметров регулятора на каждой из моделей с тем, что мы при этом получим на истинном объекте. Следует отметить, что в связи со спецификой задачи идентификации параметров дифференциального уравнения, а также с тем фактом, что в каналах измерений действует помеха, коэффициенты переда- точной функции объекта (9) получаются неоднозначными и сильно зависят от параметров модели замкнутой системы, полученных на этапе параметрического синтеза модели. Тем не менее, характер поведения выхода моделей в зависимости от структуры можно проследить (табл. 3).

Таким образом, можно сделать вывод о том, что использование модели, порядок дифференциального уравнения которой превосходит порядок дифференциального уравнения истинного объекта, при настройке параметров регулятора значительно «сужает» область устойчивости системы и, следовательно, может не привести к получению качественного управления (в случае, если оптимальные значения параметров регулятора для истинной системы не принадлежат области устойчивости системы управления моделью). В то же время, «занижение» порядка модели может привести к тому, что при качественном управлении моделью истинная система даже не окажется устойчивой. При совпадающей структуре модели и истинного объекта область устойчивости оказывается примерно одинаковой, и результаты настройки параметров регулятора на такой модели могут привести к значительному повышению качества управления истинным объектом. В связи с вышесказанным следует отметить, что при выборе структуры лучше завысить порядок модели, чтобы избежать неустойчивости истинной системы при полученных на модельной системе параметрах регулятора.