О выборе предельных режимов разброса параметров в динамических схемах ракет-носителей

Проектирование автомата стабилизации (АС) системы управления (СУ) для решения задач устойчивости движения основывается на динамических схемах ракет-носителей (РН) — математических моделях, в которых учитываются основные динамические свойства РН как объектов управления. Результаты многочисленных отечественных и зарубежных исследований по динамическим схемам РН, с учётом действия аэродинамических сил, подвижности жидкости в топливных баках и упругости их конструкций, отражены в работе [1]. Новый подход к формированию динамических схем РН, связанный с развитием вычислительной техники и широким применением современного программного обеспечения, представлен в работе [2]. Используемые при формировании динамических схем РН механические параметры известны с той или иной погрешностью. Применение статистических методов моделирования [3, 4] для выбора настроек АС с учётом этих погрешностей затруднено из-за большого количества параметров и невозможности строго независимого их вероятностного разброса, обусловленной сложными связями параметров между собой. Поэтому предлагаются два предельных режима разброса параметров динамических схем РН, упрощающих предварительный выбор настроек АС СУ для решения задач динамики РН.

Направления разбросов в низкочастотном диапазоне

В этом частотном диапазоне волновые колебания свободной поверхности жидкости в топливных баках не возбуждаются, но подвижность жидкости влияет на движение РН [2, с. 189]. При угловых колебаниях РН свободные поверхности жидкости остаются плоскими и перпендикулярными вектору кажущегося ускорения g* в программном движении, т. е. жидкость перемещается относительно стенок баков. Это приводит к изменению присоединённых моментов инерции жидкости и появлению гидростатических моментов. В низкочастотном диапазоне возмущённое угловое движение относительно центра масс РН вокруг оси тангажа может быть описано следующим уравнением:

J _* ϑ ^.. = δ M^c + δ M^a + δ M^s + δ M , (1)

где J _* — момент инерции РН; ϑ — вариация угла тангажа; δ M^c , δ M^a , δ M^s и δ M — вариации моментов управляющих, аэродинамических, гидростатических и возмущающих сил соответственно.

Моменты управляющих и аэродинамических сил:

δ M^c = x _δ P δ ;

δ M^a = QSx_Dc_y ^αϑ ,

где x _δ , x_D — продольные координаты точки приложения управляющих сил и точки фокуса аэродинамических сил относительно центра масс соответственно; P — сила тяги; δ — вариация угла поворота вектора силы тяги; Q — скоростной напор; S — характерная площадь; c_y ^α — производная коэффициента нормальной аэродинамической силы по углу атаки.

Момент инерции РН и вариация момента гидростатических сил:

J _* = J + ∑ m_snx_snl_sn ; δ M^s = g _* ϑ∑ m_snl_sn ,

где J — момент инерции РН с учётом определения присоединённых моментов инерции жидкости при неподвижной свободной поверхности жидкости; m_sn — массы осцилляторов колебаний жидкости; x_sn — продольные координаты этих масс относительно центра масс; l_sn — длина в маятниковой аналогии представления колебаний жидкости, g_*

l_sn = ₂ ; ω _sn — собственная частота;

® sn n — номер тона колебаний. Суммирование проводится по всем тонам колебаний жидкости.

Закон управления угловым движением принимаем в следующем виде:

.

δ = K ₁ ϑ + K ₂ ϑ ,

где в низкочастотном диапазоне коэффициенты K ₁ > 0; K ₂ > 0 можно считать постоянными. Подстановкой соотношений (2), (3), (4) уравнение (1) приводится к следующему виду:

8 M

..                .

ϑ + βϑ + ω ² _* ϑ = _J ,                   (5)

*

• ^{-K 2 x 8 p} где коэффициент β = J . *

Из уравнения (5) следует, что в управляемом движении РН характерная частота угловых колебаний определяется следующим образом:

ω

*

^-K i x s ^{P -} QSx D c y ^- g * ^E mj^ J_*

где x _δ < 0; x_D > 0; c_y ^α > 0. Частота ω _* является важной динамической характеристикой — чем выше эта частота, тем быстрее отрабатываются отклонения от программного движения. Для быстрого затухания переходных процессов при действии возмущений система управления должна обеспечивать оптимальное демпфирование угловых колебаний РН, которое характеризуется коэффициентом β .

Необходимо отметить, что центр масс не является точкой безразличного равновесия РН в поле массовых сил, поэтому частота ω* должна определяться с учётом действия гидростатических моментов жидкости в топливных баках. Точками безразличного равновесия системы твёрдое тело – жидкость со свободной поверхностью являются метацентры [5].

Предельные расчётные случаи определяем разбросами параметров динамической схемы, при которых частота ω _* принимает минимальное и максимальное значения.

В повышенном режиме (с максимальными аэродинамическими моментами) частота ω _* может быть минимальна, если направление разбросов таково, что

∆ P < 0;

∆ J _* > 0;

(6) ∆ x_D > 0;

∆cyα > 0, а положение центра масс в базовой системе координат смещается вниз, и при этом |xδ| уменьшается, а xD — увеличивается.

В пониженном режиме (с минимальными аэродинамическими моментами) частота ω _* может быть максимальна, если направление разбросов таково, что

∆ P > 0;

∆ J _*< 0;

(7) ∆ x_D < 0;

∆cyα < 0, а положение центра масс в базовой системе координат смещается вверх, и при этом |xδ| увеличивается, а xD — уменьшается.

Направления разбросов гидродинамических параметров колебаний жидкости

Как правило, для устойчивости движения на частотах колебаний жидкости в топливных баках требуется фазовое опережение АС, которое необходимо для устойчивости движения РН на низких частотах. При фазовом опережении действие АС приводит к увеличению демпфирования колебаний жидкости.

Если на одной из собственных частот колебаний жидкости в баках к АС предъявляется противоположное требование фазового запаздывания, то проявляется так называемая структурная неустойчивость [5], обусловленная расположением баков в составе РН. При структурной неустойчивости, наиболее опасной для автономного полёта верхних ступеней РН и разгонного блока (РБ), действие АС приводит к подводу энергии в колебания жидкости. На участках полёта верхних ступеней РН и РБ возможна также собственная динамическая неустойчивость с подводом энергии в колебания жидкости неконсервативной следящей силой тяги двигателя [5, 6]. Как правило, в этих случаях для обеспечения устойчивости требуется повышение диссипации энергии колебаний жидкости, которое достигается установкой в топливные баки демпфирующих перегородок [7].

Снижение частоты колебаний жидкости приводит к уменьшению фазового опережения, создаваемого АС, и ухудшает качество переходных процессов на тех тонах колебаний жидкости, для которых требуется фазовое опережение АС, но при этом несколько снижается требование к демпфированию структурно неустойчивых тонов колебаний жидкости.

В повышенном режиме снижение частот колебаний жидкости происходит из-за уменьшения силы тяги двигателей. Дополнительное снижение частот колебаний жидкости может быть обусловлено пониженным уровнем топлива в баках, из которых оно не вырабатывается, и наличием демпфирующих перегородок. Как правило, на участке полёта первой ступени уменьшение уровня топлива в баках верхних ступеней РН и РБ приводит к увеличению массы осцилляторов колебаний жидкости, а увеличение уровня заливки — к увеличению частот и уменьшению массы осцилляторов колебаний жидкости.

В повышенном режиме , принимая во внимание приведённые сведения, предлагается принимать следующие направления разбросов гидродинамических параметров:

∆ω _sn < 0;

∆ m_sn > 0;                               (8)

∆β sn < 0.

В пониженном режиме предлагается принимать следующие направления разбросов гидродинамических параметров:

∆ω _sn > 0;

∆ m_sn < 0;                               (9)

∆β _sn < 0.

Коэффициенты демпфирования β _sn связаны с логарифмическими декрементами колебаний зависимостью

∆

sn

лВ sn

О

sn

Разбросы удобнее задавать

не на коэффициенты демпфирования β _sn и частоты ω _sn , а на безразмерные декременты колебаний ∆ _sn и безразмерные частотные параметры

ю ² R

κ

n

sn n

g

в которых R_n

характерный

размер соответствующего бака.

Разбросы на координаты масс осцилляторов ∆ x_sn можно не задавать, т. е. принимать ∆ x_sn = 0. Влияние разбросов на эти координаты в достаточной мере учитывается разбросами на координаты центра масс РН в базовой системе координат. Разбросы на коэффициенты демпфирования колебаний жидкости для повышенного и пониженного режимов задаются в сторону уменьшения, так как ухудшают условия устойчивости.

Направления разбросов характеристик упругих колебаний

В максимально упрощённом виде движение РН вблизи частоты одной из собственных форм упругих колебаний описывается следующим уравнением:

q ^.. _k + β _qk q^._k + ω _q ² _kq_k = δ Q_k^c + δ Q_k , (10) где q_k — обобщённая координата упругих колебаний конструкции РН; k — номер формы упругих колебаний; β _qk — коэффициент демпфирования; ω _qk — собственная частота. Вариация обобщённой управляющей силы

δ Q k ^c = u k P δ ,

где u_k — величина формы перемещения упругих колебаний в точке приложения управляющей силы, а δ Q_k не зависит от обобщённой координаты q_k и может учитывать влияние остальных степеней свободы.

Закон управления (4), пренебрегая в рассматриваемом резонансном режиме колебаний влиянием всех остальных степеней свободы, запишем приближённо в следующем виде:

δ = K 1 ϑ k q k + K 2 ϑ k q^. k , (12)

где ϑ _kq_k и ϑ _k q^._k — измеренные значения угла поворота и угловой скорости при упругих колебаниях. Подставив выражения (11), (12) в уравнение (10), получим

• q^.. k + ( β qk – K 2 u k ϑ k P ) q ^. k +

+ ( ω ² qk – K 1 u k ϑ k P ) q k = δ Q k .              (13)

Как видно из уравнения (13), АС изменяет как частоту, так и демпфирование упругих колебаний конструкции РН.

Условие устойчивости упругих колебаний:

^K 2 U k ^ k ^P

P qk

< 1.

Если K ₂ > 0 и u_k ϑ _k < 0, то АС увеличивает демпфирование упругих колебаний конструкции РН. Если K ₂ > 0 и u_k ϑ _k > 0, что типично для низшей формы упругих колебаний, то АС подводит энергию в эти колебания.

Из условия (14) следует, что задание однонаправленных разбросов на разные формы упругих колебаний не имеет смысла, так как эквивалентно заданию разбросов на коэффициенты демпфирования. Задание разнонаправленных разбросов на формы упругих колебаний возможно по результатам проведения анализа динамических свойств частотными методами при номинальных параметрах динамической схемы. Сближение частот колебаний жидкости с частотой низшей формы упругих колебаний может приводить к изменению условий устойчивости на частотах колебаний жидкости.

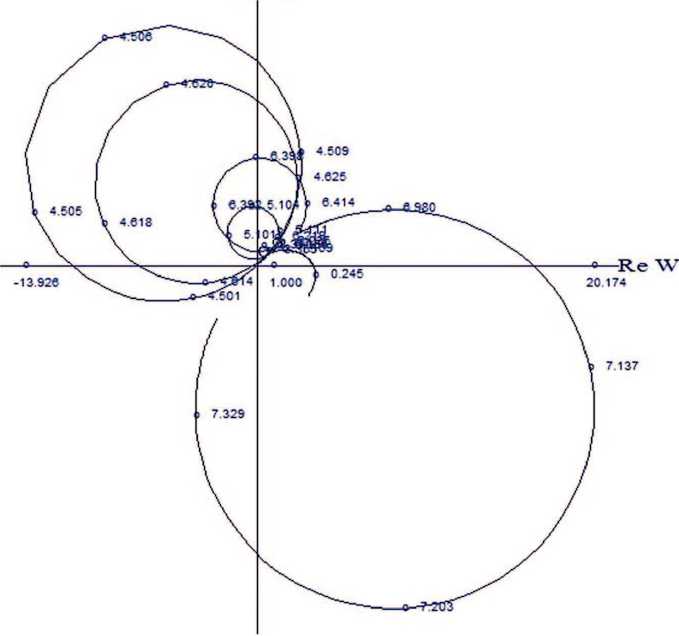
На рис. 1 представлены результаты анализа частотным методом Найквиста динамических свойств ракеты космического назначения «Ангара-А5» с РБ ДМ в один из моментов времени полёта первой ступени. Собственная частота первой формы упругих колебаний конструкции равна 1,1 Гц, а собственные частоты колебаний жидкости в баках находятся в диапазоне 0,7…1,0 Гц. Оцифровка на графиках приведена в значениях круговой частоты. Диссипация энергии колебаний жидкости принята на уровне, характерном для баков без демпфирующих перегородок, а упругих колебаний — на уровне 1% от критического значения. Коэффициенты АС СУ выбраны так, чтобы при действии момента аэродинамических сил с достаточным запасом обеспечивалась устойчивость на низких частотах.

Годограф Найквиста на рис. 1, а построен в диапазоне частот 0,02…1,20 Гц без учёта связи между колебаниями жидкости и упругой конструкции. Как видно, обеспечивается асимптотическая устойчивость на частотах колебаний жидкости во всех баках. Для устойчивости на частоте упругих колебаний к АС СУ предъявляется стандартное требование фазового запаздывания.

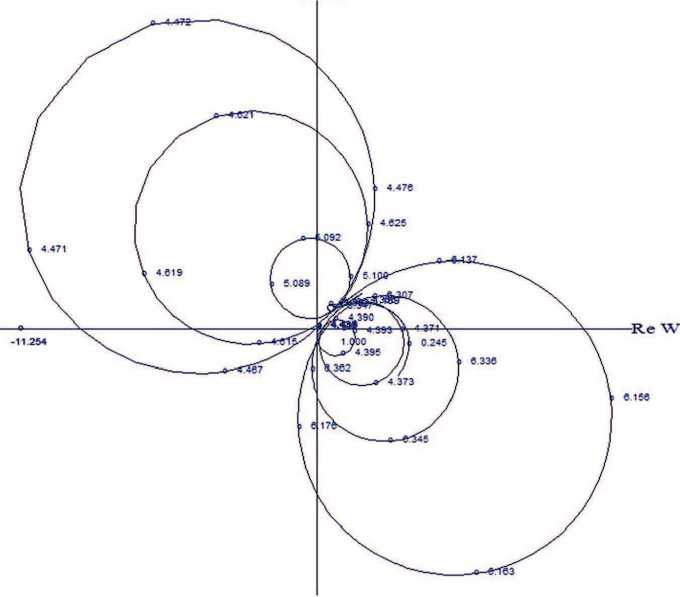
Годограф Найквиста на рис. 1, б построен в диапазоне частот 0,02…1,10 Гц с учётом связи между колебаниями жидкости и упругой конструкции. Ветвь годографа, соответствующая упругим колебаниям, практически не изменилась и не показана. Как видно, динамические свойства в диапазоне частот колебаний жидкости сильно изменились. На частотах некоторых тонов колебаний жидкости к фазовой характеристике АС СУ предъявляется противоположное требование фазового запаздывания. Поэтому при формировании динамических схем РН необходимо использовать разбросы с максимально возможным разнесением и сближением частот колебаний жидкости и упругих колебаний конструкции.

В повышенном режиме предлагается принимать следующие направления разбросов динамических характеристик упругих колебаний:

∆ω _qk > 0;

∆ u_k = 0;

∆ϑ _k = 0;            (15)

∆β _qk < 0;

∆ω_δ < 0.

В этом режиме разбросов частоты колебаний жидкости и упругих колебаний, учитывая условия (8), в которых ∆ω _sn < 0, разнесены. Направления разбросов частот упругих колебаний и частоты подвески управ-

Im W

а)

ляющих маршевых двигателей ω_δ должны быть разнонаправлены, чтобы учесть взаимодействие разных форм упругих колебаний с упругой подвеской управляющих двигателей.

В пониженном режиме предлагается принимать следующие направления разбросов динамических характеристик упругих колебаний:

∆ω _qk < 0;

∆ u_k = 0;

∆ϑ _k = 0;            (16)

∆β qk < 0;

∆ω_δ > 0.

В этом режиме разбросов частоты колебаний жидкости и упругих колебаний, учитывая условия (9), в которых ∆ω _sn > 0, сближены.

Im W

б)

Рис. 1. Графики Найквиста без учёта (а) и с учётом (б) взаимодействия колебаний жидкости в баках с упругими колебаниями конструкции: Im W и Re W — мнимая и действительная части частотной характеристики соответственно (рисунок создан автором)

Условия (6), (8), (15) определяют направления разбросов в повышенном режиме, а условия (7), (9), (16) — в пониженном режиме во всём диапазоне частот. Две предельные неноминальные динамические схемы формируются путём изменения по определённым направлениям механических параметров, заданных в исходных данных крайними значениями разбросов по каждому из параметров.

Выводы

Предложены два предельных режима разброса параметров динамической схемы РН, упрощающих проведение моделирования возмущённого движения и предварительный выбор настроек АС СУ для решения задач динамики. Учитываются случайные разбросы инерционно-массовых характеристик, сил тяги двигателей, аэродинамических характеристик, гидродинамических параметров колебаний жидкости, упругих характеристик конструкции и подвески управляющих маршевых двигателей, связанные с погрешностью их определения. Разработанный подход применялся при выборе предельных режимов разброса параметров для формирования динамических схем РН «Ангара-А5» с разгонным блоком ДМ.