О вычислительной эффективности алгоритма спектрального расщепления проверки изоморфизма графов

Мы рассматриваем эвристический алгоритм проверки изоморфизма графов. Алгоритм основан на последовательном расщеплении кратных собственных значений матриц, сопоставленных графам: матрицы, с которыми работает алгоритм, представляют собой модификации матриц смежности графов. Алгоритм строится на последовательном возмущении матриц и решении связанных с ними систем линейных алгебраических уравнений. Матрицы видоизме-нёны до положительно определенных, что позволяет решать системы линейных уравнений, связанные с ними. Доказывается вычислительная эффективность алгоритма в одной из принципиально тяжелых для решения задачи проверки изоморфизма графов ситуаций.

Алгоритм спектрального расщепления проверки изоморфизма графов

Задача проверки изоморфизма графов принадлежит к задачам, относительно которых нет ясности: являются ли они полиномиально разрешимыми или нет [1], тогда как известно, что она является полиномиально разрешимой для некоторых классов графов. В частности для планарных, регулярных графов, графов с ограниченной степенью вершин, графов с ограниченной кратность собственных значений из спектра матрицы смежности и некоторых других[4], [5], [6] построены эффективные алгоритмы решения этой задачи.

В задаче проверки изоморфизма графов даны два неориентированных графа G A = { V A , E A ) и G B =( V B , E B ) , где V A , V B — множества вершин графов, E_A , E_B – множества ребер. Везде далее графы G_A и G_B – связные. Предполагается, что I V A = ы^, I E A I = I E « I-

Задача изоморфизма графов формулируется следующим образом: существует ли биективное отображение p : V A ^ V B , такое, что ( i , j ) е E A , то ( р ⁽ i ), р (j )) е E B ?

Алгоритм решения задачи определения изоморфизма графов работает с видоизмененными матрицами смежности графов. Пусть A ₀ – матрица смежности графа G A , то есть A 0 = ( a. ), где

Г 1,( i , j ) е E_a , a n = k A

I 0, иначе.

B 0 = ( b . ) - матрица смежности графа G B .

По матрице a ₀ строим матрицу D _{A 0} :

^ d + d i         00

• X ••

0 d + d. 0.

•• X •

^ 0     ..     0      .. d + dn

D_{A 0} – диагональная матрица, где:

di = ^Lay, j * i то есть di– степень вершины i графа GA , d = max di.

1 < i <  n

Аналогично строится матрица D_{B 0} по матрице смежности графа G_B . Рассматриваемые далее матрицы

A = A 0 + D A 0 , B = B 0 + D b 0                  (1)

– матрицы, с которыми будет работать алгоритм, являются симметрическими положительно определенными матрицами.

Если графы G A =( V A , E A ) и G b =( V b , E b ) изоморфны, то соответствующие им матрицы описанного типа могут быть получены одна из другой перестановкой строк с одновременной перестановкой столбцов с теми же номерами. Таким образом, задача проверки изоморфизма двух графов может быть сформулирована как частный случай задачи Фробениуса: может ли быть получена матрица B из матрицы A последовательной перестановкой строк с одновременной перестановкой столбцов?

Для произвольной матрицы перестановка строк с номерами i и j эквивалентна ее умножению на матрицу перестановки P_ij . Перестановка столбцов матрицы эквивалентна ее умножению справа на ту же матрицу. При умножении вектора на матрицу P_ij как справа, так и слева происходит перестановка компонент вектора с номерами i и j .

Рассмотрим две системы уравнений следующего вида:

Ax = e . , By = e k ,                             (2)

где векторы ei = (0,. ,0,1,0,. ,0) - базисные векторы в пространстве R n , матрицы A и B – описанного выше вида. Обе системы уравнений имеют решение, и решение единственно, так как A и b – матрицы с диагональным преобладанием, и, следовательно, их определители не равны нулю. Пусть далее xj -решение системы линейных уравнений Ax = ej, yk - решение системы линейных уравнений By = ek.

Отметим, что решив системы уравнений (2), мы получим обратные матрицы для матриц A и B . Так, для i -ой компоненты вектора x j верно: x ji = A j / | A |, где A j - алгебраическое дополнение элемента a ji матрицы A . То есть векторы решений X j , 1 <  j <  n , являются столбцами обратной к A матрицы.

Если B = P jk AP jk , то для решений систем уравнений (2) должно выполняться равенство: xP jk = У . Действительно:

(A^x = e j ) ~^(p jk A^X = P jk e j ) ~

~ (P jk AxP jk = P jk e j P jk ) ~(P jk AP jk X = e j )

~ (P jk AP jk XP jk = eP) ~(BxP jk = e k ) .

То есть xP jk = y .

Если матрица B получена из матрицы A многократной одновременной перестановкой строк и столбцов, то: ^B = P j)! • P A k 1 ^AP j₁ k 1 • " j - и, соответственно, ^xP 1 4 • jl = У .

Таким образом, если в системе уравнений (2) при фиксированном j индекс k будет пробегать значения от 1 до n , то векторы x j и y_k - соответствующие друг другу решения полученных систем (2) будут совпадать с точностью до перестановки компонент только в том случае, если строке j матрицы A соответствует строка k матрицы B . То есть элементы строки k матрицы B есть переставленные элементы строки i матрицы A . То же верно и для столбцов матриц.

При нахождении в матрице B строки и столбца, соответствующих строке и столбцу с номером i матрицы A , на каждой итерации алгоритма будем последовательно производить возмущения ее диагональных элементов.

Алгоритм работает с симметрическими матрицами, которые могут быть приведены к диагональной форме с помощью ортогональных преобразований. То есть:

A = UaAUa, B = UbBUb, где A~ , B~ - диагональные матрицы, с собственными значениями на диагонали, UA , UB - матрицы ортогональных преобразований, UA, U'B -транспонированные к ним матрицы. Диагональные элементы A~ , B~ - собственные числа матриц A и B .

Спектры матриц смежности изоморфных графов совпадают[2]. Спектры матриц вида (1) изоморфных графов будут совпадать тоже, так как описанная выше процедура замены нулевых диагональных элементов матрицы смежности приводит лишь к сдвигу спектра матрицы. Причем, если матрицы соответствуют изоморфным графам, то спектры матриц будут совпадать и после сдвига.

Если спектр каждой матрицы является простым, или кратность собственных значений мала, то задача проверки изоморфизма графов разрешима однозначно путем сопоставления строк матриц U A , U_B , A , B [3]. Матрицы U A , U B могут иметь, например,

следующий вид: ' v 11 v 12 v 13 v 14 v 15 ' v 21 v 22 v 23 v 24 v 25 Ua = v 31 v 32 v 33 v 34 v 35 v 41 v 42 v 43 v 44 v 45 . v 51 v 52 v 53 v 54 v55 y v 31 v 32 v 33 v 34 v35 ^ v 21 v 22 v 23 v 24 v 25 Ub = v 11 v 12 v 13 v 14 v 15 , v 51 v 52 v 53 v 54 v 55 . v 41 v 42 v 43 v 44 v 45 > где {Vj} j =i - собственные векторы матрицы A . То есть строки матриц, составленных из собственных векторов, те же с точностью до перестановки, задающей изоморфизм.

Основные трудности возникают при рассмотрении графов, спектры которых содержат кратные собственные значения. Возмущая матрицы в ходе итераций алгоритма, мы будем получать возмущение спектра матриц, при котором происходит расщепление кратных собственных значений, что позволит установить однозначное соответствие между строками и столбцами матриц.

В результате, после того как кратные собственные значения матриц A и B в ходе работы алгоритма будут расщеплены, будет возможно однозначное определение перестановки, задающей биекцию ф , устанавливающую изоморфизм графов

Ga = < Va , Ea ) и Gb = ( Vb , Eb ).

Приведенный ниже алгоритм, однако, работает не с собственными векторами, а с векторами, являющимися столбцами обратной матрицы к матрице A , и в качестве характеристик, на основе которых строится соответствие между вершинами графов, рассматриваются компоненты и нормы этих векторов. Норма:

n

II^INE x ik .

V k = 1

В этом случае невозможность установления однозначного соответствия возникает при наличии среди этих векторов группы векторов, которые могут быть получены друг из друга с помощью перестановки их компонент, и, следовательно, имеют одинаковые нормы. При этом компоненты этих векторов, образующие диагональ обратной матрицы, совпадают. Однако, при возмущении матрицы, влекущем расщепление ее собственных значений, происходит как возмущение ее собственных векторов, так и возмущение вектор-столбцов обратной к A матрицы. В результате описанные выше группы векторов с одинаковыми нормами расщепляются.

Пусть x_i и x_k – вектор-столбцы обратной матрицы такие, что x i = Px_k для некоторой матрицы перестановки P , и их компоненты, лежащие на диагонали обратной матрицы, равны: x i = x k . В ходе работы алгоритма на каждой итерации будем работать не с исходными, но уже с возмущенными в ходе предыдущих итераций алгоритма матрицами. Получив соответствие строки j матрицы A ^j строке k матрицы B ^j на j -ой итерации, а также столбцами с теми же номерами, рассматриваем далее возмущенные матрицы A^{j +} 1 и B^{j +} 1 :

A^{j + 1} = A^j + _£ jEJ , B^{j + 1} = B^j + _£ jE^k .

Возмущения производим с помощью матриц E с элементами e : q                               ij

/ 1, i = ^j = q , e ij     In „ _

1 0, иначе.

Численные эксперименты показывают, что расщепление спектра матриц, необходимое для определения соответствующих друг другу строк и столбцов матриц, происходит значительно раньше заключительной итерации. К примеру, для графов, представляющих собой решетку на торе с числом вершин n от 9 до 400, уже на итерациях с номером n не требовалось дальнейших возмущений диагональных элементов матриц A и B для установления однозначного соответствия между вершинами графов.

В результате, если матрица B может быть получена из матрицы A последовательными одновременными перестановками строк и столбцов, то в ходе работы алгоритма, пока j пробегает значения от 1 до n , будет получена перестановка строк и столбцов матрицы A – перестановка P . Перестановка P является, вообще говоря, одной из возможных перестановок. То есть, как подстановка P выглядит следующим образом:

[ 1   2 n )

P = 1,                       I

Uk 1 k 2 ••• kn )

где kj – номер строки матрицы B , полученный на j -й итерации. Перестановка P задает такую перенумерацию вершин графа GA , то есть отобра- жение ф: VA ^ VB , при которой матрицы A и B , представляющие графы, совпали бы, что возможно только в случае изоморфности графов.

Алгоритм спектрального расщепления проверки изоморфизма графов

Шаг 0. A ⁰ : = A, j: = 1. P(i): = 0 , 1 <  i <  n .

Шаг 1 . Если j <  n , то Шаг 1.1 . , иначе - работу алгоритма завершить.

Шаг 1.1.

£ j := ( d + d j )² + - [| | A , -|| + 2 + - |-( d + d j ).

^J v ^J n U^{1 711} n)            ⁷

Шаг 1.2. A^j: = A^{j + 1} + £ j E^j .

Шаг 2. Решение системы

уравне-

ний A ^j

x = C j . x j

– полученное решение.

Шаг 3. k: = 1. Если k <  n , то - Шаг 3.1, иначе перейти на Шаг 4.

Шаг 3.1. B_k: = B^{j + 1} + £ j E^k .

Шаг 3.2. Решение системы уравнений

B^ky = c_k . y_k - полученное решение.

Шаг 3.3. k: = k + 1. Перейти на Шаг 3.

Шаг 4. Сравнение норм векторов x_j и y_k ,

• k : V i <  j : P ( i ) * k .

Если V k : | x j ||^|| y_k ||, то графы G A и G_B неизоморфны.     Работу алгоритма завершить.

Если 3 k : || x j 11 = | \y_k 11 и x j = y k , то P(j): = k (вершине j графа G_A ставим в соответствие вершину k графа G_B ), B_k: = B^{j +1} + £ j E^k .

Шаг 5. j: = j + 1.

Шаг 6. Решение систем уравнений A^jx = c l : V i P ( l ) * i . x l - полученные решения.

Шаг 7. Если V p , l : || x l 11 * || x p 11 , то перейти на Шаг 8, иначе перейти на Шаг 1.

Шаг 8. Если j <  n , то решение систем уравнений для всех i таких, что P ( i ) * p .

Шаг 9. Сравнение норм полученных решений:

Если 3 p , l : | x i 11 = || y p |^ V i P ( l ) * i , V i P ( i ) * p , то P(l): = p .

В действительности в связи с погрешностями вычислений проверяются близости норм, а не их равенства, и хотя алгоритм спектрального расщепления проверки изоморфизма графов хорошо зарекомендовал себя в ходе вычислительных экспериментов, следует отметить, что для произвольных графов нельзя гарантировать получения решения задачи изоморфиз- ма графов с помощью представленных схем алгоритма. Так, представляется допустимой ситуация, когда проверки векторов на равенство (близость) норм на шаге 4 алгоритма и проверки равенства (близости) компонент xjj и ykk недостаточно для ответа на вопрос, может ли вектор yk быть получен из вектора xj последовательной перестановкой его компонент.

При установлении соответствия между вершинами графов, алгоритм спектрального расщепления:

• 1)    проверяет равенство, а в связи с погрешностями вычислений, в действительности проверяется близость норм решений систем линейных уравнений Ax = e j и By = e j , 1 <  j <  n ;

• 2)    в случае равенства норм векторов x_j и y_k проверяется равенство (близость) компонент jk

этих векторов x_j и y_k .

Таким образом, для ответа на вопрос об эффективности алгоритма спектрального расщепления для проверки изоморфизма графов G_A и G_B необходимо оценить насколько будут отличаться после последовательных возмущений матрицы A нормы векторов x _i и x _j , соответствующих разным вершинам графа G_A .

Эффективность алгоритма

Везде далее будем использовать следующие обозначения:

A,, 1 < i < n - вектор, компоненты которого являются элементами i -й строки матрицы А, U – обратная матрица к матрице A , Ui, 1 < i < n - вектор, компоненты которого являются элементами i -го столбца матрицы U (Ui = xi), ai - угол между вектором Ai и ортом ei , pi - угол между вектором Ui и ортом ei, yi - угол между вектором Ai и ортом Ui.

Будем также считать, что максимальная степень вершин графа ( d ) не менее 3. Ситуация, когда максимальная степень вершин графа менее 3, не представляет интереса с точки зрения проверки изоморфизма графов.

При возмущении диагонального элемента a _jj матрицы A возрастает j -я компонента вектора A_j . То есть при возмущении диагональных элементов матрицы происходит приближение векторов {A j } n = 1 к соответствующим ортам e j декартовой системы координат в Rⁿ .

Действительно, пусть a j - угол между вектором A_j и ортом e_j , тогда:

(Aj,ej) ajj cos a j = ИМ=PJ"

ajj = dj + d + e j,

I Aj 11 = , I a 2j '- a 2k = V(dj + d + 8j )2 + dj • Та-V      k * j ким образом, d j + d + 8

cos a j

d

1 +-------- j -----7

.

d = max d j, и, следовательно, при возмущении диа-j гональных элементов матрицы cos a j, j = 1 < j < n, будет приближаться к единице, а сами углы a j, соответственно, к нулю.

Столбцы обратной матрицы к A матрицы U – векторы {U j }" = 1 образуют систему векторов, каждый вектор U _j из которых ортогонален всем векторам A k , k * j , и (A j , U j ) = 1, так как UA = I .

Векторы {U j }" = i близки по направлению к векторам     {A j } j = 1 .    Действительно, так как

U j ± A k , k * j , то U j определяет гиперплоскость в пространстве Rⁿ , в которой лежат векторы A k , k * i . В процессе возмущения матрицы векторы {A k } k = 1 приближаются к ортам {e k } к = 1 , а значит и гиперплоскость, натянутая на векторы A k , k * j , приближается к гиперплоскости Rⁿ\L_j , где L_j – одномерное линейное пространство, натянутое на орт e_j . Таким образом, и вектор U j будет приближаться к реперу e_j , и, следовательно, угол между векторами U j и A j будет уменьшаться

Лемма 1. Для произвольной матрицы вида (1), представляющей граф, для любого j

3 d ^cos ? ^>-/=ii. ^j 10 A j

Доказательство

Угол вj равен углу между гиперплоскостью Rn\Lj и гиперплоскостью Rn\L(U j ) , где L(U j ) – одномерное линейное пространство, натянутое на вектор U j . Гиперплоскость R n\L(U j ) натянута на векто- ры Ak, k * j,    так как

U j V ( R n \L (U j ) ) ,

e j 1( Rⁿ\L j ) . Следовательно V k, k * j , б_k >  в j , а

значит dt + d cos p j > max —--- k*j (/(dk + d)2 + dk

(Uj, ej)    Ujj cos e j = —гиг = ii—Г, значит j    Uj ej Uj

U jj             dk + d           1       3

> max        = > ---= -= .

|U j i    ^k * j V( d k + d )2 + d k    Г| <-

1                  1 f iiAnUii iia-1u;ii  inkи U;iи

= NU M^{( U j 1-1} U⁶

По правилу треугольника из U i - U i + U i = U i следует:

I Ui- Ujl+и> lU-l или

| Ui - u ;| |> U - 1|- U i l |.

То есть

( U j , A j )         1

cos j КкГ И1Ы

> ³

10 A j U jj ^.

| cos y -

- cos y - I <

I Ai lNl Ui li* ^Ui

-

^U, i (4)

Известен следующий результат Фань-Цзы [7].

Пусть A – матрица с диагональным преобладанием, и si = |a--1-^aik . Если si > 0, то k * i существует обратная к матрице A матрица A', и

I a 'i\< -, ¹ <  i <  n .

si

В нашем случае, матрица A , ставящаяся в соответствие графу G_A , – матрица с диагональ-

ным            преобладанием,            и si = d + di - di = d ; Uy | = Uj , следовательно,

Uji < - jj_d

и

3           3d cos Yj > I----II II > /----II II . j 10AjUjj 10Aj

Лемма 1 доказана.

Пусть далее векторы и углы со штрихом – векторы и углы, в которые переходят соответствующие им нештрихованные векторы и углы в ходе итерации алгоритма.

Лемма 2

( U i , A j ) = 0, тогда как

( U ; , A j ) = (U ; , A j + ^ e j .) = (U i , A j ) + (U i , ^ e j .) = 0, сл едовательно:

( U i , A j ) = Sj U j .

И поэтому

(U i - U i , A j ) = S j U ij .                            (5)

Из (4) и (5) следует:

£j\Uj\

1 cosy‘" cos Y,klA,l|U,IIHA,l^os n ■ где n - угол между вектором Uj - Ui и Aj .

V k * j :(U ; - U i , A_k ) = 0, а так как векторы { A k } k = i образуют базис в R n , то, учитывая (5), получаем, что при возмущении вектора A_j происходит изменение U_i в одном из двух возможных направлений – или в направлении вектора A_j , и тогда cos n = 1, или в направлении противоположном вектору A j , и тогда cos n = - 1, и значит,

еj

I cos y - cos Y I < iTTii- i i       Ai

Доказательство

|cos y - - cos Y i j <

^£ j

U'.. ij

II ^A; III ^U Л U ;II ^A; II

^£ j

U ij

cos y i - cos y -

II A - II U II H Ui U ii

I ^Ui l Ai

£ _j ^cos Y i < ГП|.

Ai

£

То есть cos y- - cos y '• < ir j r Лемма 2 доказана. i i _Ai

Лемма 3

cos Y j =

1+

V

^e J A JJ

I A J I A

cos y J .

J

cos y j =

1+

V

e A i

I AJIIAI J

cos y .

Доказательство cos Yj = ii—iiii—ii, cos Yj = j AjUj j

------- и

II A ;i r j Г

cos Y j - cos y J

I AMA j| U J l

fl ^u j l- U J l) (6)

Лемма 3 доказана.

Вернемся теперь к исходной задаче. Для того, чтобы определить эффективность алгоритма, нам необходимо оценить снизу разность норм векторов U J и U J после увеличения J -го диагонального элемента

Векторы U j и U J имеют следующие ком-

матрицы на некоторое e j■ , при условии равенства норм векторов U _i и U до возмущения, и, соответст-

поненты:

_п    ^f AJ ¹ Aj 1   IT' -^f A ^J1 AJn '

Uj   V Ai ’ ^, iai J,UJ V A1 , ^, Aj j где A J , |A J, соответственно, - алгебраическое дополнение к элементу ak  и определитель возмущенной матрицы. Но, так как на -ой итерации возмущается только элемент a матрицы A , то Vk Ajk = Ajk . Значит

венно, cos y i = cos y j .

Iи- U Uh

II A j||^cos y j -I A ¹1l^cos y i II A J-||^cos y J -I A ^Jl I^cos y i

I A J-||^cos y j ^-lI A ^JIl^cos y i

I A J llll A ill

, f A l A n J ^j V i a j a j.

Следовательно,

I ^U J I- ^u J11=

n 2

^A k

1 ^EI A I²

n 2

^A k

11 ^E I A 1²

n

=,Z A 2k

V k = 1

1      11

V

I A l I A 1J \

n

E A 2k k = 1

I A 'H A l'

I A 'll A l

>

До возмущения     матрицы:      ||aj || = || A i 11.

||A J || = || A i ||, так как возмущение не затрагивает J -ю строку матрицы. Пусть e ji такое, что || A J || = || A i 11 + e ji . Тогда (7) эквивалентно

IИ- U i l|>

(IIAII + ^e Ji ^)cos y j ^-lIAII^cos y i

II A J llll A JI

Рассмотрим числитель выражения выше. Пусть

^S = (I I A II ^{+ e} ii ) cos y j ^- 1 I A II cos у'¹ = I I A ll^(cos y j ^-

-cosy1) + eji cosyj =||Ai||(cosyj -cosYjJ) + ||Ai||x x (cos yi - cos yi) + eji cos yj,

Возмущение определителя: A j = | A | + e j A^ .

И таким образом:

i U j I- u h=^ A J

Возвращаясь к (6), получаем: n 1                ,2 e^ii cosyj-cosyj = IAjUAiluJlA J‘AM

и

S 1 =| I A i ||^(cos y j ^{- cos} Y j• ),

^S 2 =|| A i ||^(cos Y i ^{- cos} y i X

S 3 = ^e ii ^cos y j, ( S = S ₁ + S ₂ + S 3 ).

Лемма 4

IS J > Is 2I nn

I ^u ill- й iE A 2k , W ^u E A ■

I A I V k = 1                        v k = 1

Доказательство

По лемме 3

(

следовательно,

^S 1 =1 A i l

1 +

cos y j - cos y j =

^e i A j

n

E A i.

k = 1

^e J A jj

IAJIIAI

cos y ^.

по лемме 2

V

^e j A Jj

I A JII A I

cos y , J

А, значит,

e;

^{S 2} A i A i i^{= e} j .

Следовательно,

(              3

"^{+ S} 2 >' ^l¹⁺ й й I

cos Y j - ^£ j =|HUcos / j ⁺

оценки снизу модуля разности 1 ^ ‘Ц- | и ‘• учитывать

только S ₃ . То есть

+ 8 i M i l M i cosy, - 8 .

11 и Я Н   j-   j

3d cos у, > .——й , по лемме 1.

^j 10 A j

S = S 1 + S ₂ + S ₃ >  S ₃ = £ ji cos / j- .

По лемме 1

cos у j >

3 d

10 A j ^.

Если

Таким образом,

3d 3d   Ai Ajj di + S>      + £        •      •       £ .

^{1   2}  л>   j л> h j i и

Оценим, каким должно быть £ j для того, чтобы выполнялось необходимое нам неравенство 1

^£ ji > -.

n

Пусть

^£ ji

+ £ , -)² + d i - V ( d + d i )² + d i = ¹ + 8

n

^£ ji > - , ^то n

S >   3 d >     3 d а/1°| |и-||п V10n V 4 n2 + n

Тогда

I U i- U ; | >

(||И i ||+ £ -i )c^os Y j -| j 4 -||c^os y ’

S

S ₃

I hj||M ' || > || и-|||И '||

3 d

>> ЛоnV 4 n2+n|Hj||M; II где 8 > 0. Откуда получаем, что

>

n

£ j = А ( n )² + 2 А ( n )J( d + d j )² + d j + ( d + d j )² —

то есть

- ( d + d j ), где A ( n ) = — + 8 , а 8 - мало.

n

£ j = ^ ( d + d j )² + 2 A ( n )^( d + d j )² + d j + A ( n ) 2 -

I U i- U I >

10 0 n (4 n ² + n

- ( d + d j ) <  ( d + d j )J1 + 2 A ( nУ169- ■ (6' -

Таким образом, нами доказано следующее утверждение.

Утверждение

Если Ц/j 11 = || U i || и £ j , такое что:

- ( d + d j ).

• a jj ^{+ £} j ^{)2 +}

Таким образом,

'a j + d j >  1, n

1          1-1 о 1-1-3 i

£j <- 8^ n )-- 8 ²( n ) +------ 8 ^,3( n ) +

j

то после j -й итерации алгоритма

1 - 1 - 3 • 5

+--

2 • 4 • 6 • 8

I U i i- U ; |>

8 '⁴( n ),

I n ² + n )2

\ ^19 - ( n )² где ^{8 (} n ) = ^{2 - (} n ) — +       .

3 d

Итак, £ j < —==, поэтому j ₁₀

S 1 + s ₂

3 d

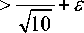
3 d   A i    A jj

-------------------•------------------•---------------- 710 I ^йj| M l

^{- £} j > ⁸ 0 ,

Таким образом, если погрешность вычислений будет, к примеру, на порядок меньше разницы точных значений норм векторов Цг'j || и U '||, то на каждой итерации алгоритма возможно выделение одного вектора из группы векторов с одинаковыми нормами.

Пусть решение систем линейных уравнений осуществляется с помощью метода Зейделя. Приближения к точному решению на m -й итерации метода Зейделя могут быть оценены как

где 8 ₀ >  0 .

То есть      S 1 + S ₂ >  8 0 , |S 1| > | S ₂| + 8 0 , и

|S 1 1 > | S ₂|. Лемма 4 доказана.

В итоге, доказав леммы выше, мы можем отбросить слагаемые S ₁ и S ₂ , и для построения

U j - U~ j ( m )|| <  ^ ” 8 °, | U j

U ~ j⁽ m ) < ^ " 8 °,

здесь 8i0,8j - погрешности начальных приближе-~~ ний Ui, Uj , Ui( ), Uj( ) - приближения Ui, Uj на m - й итерации метода Зейделя, а

d k

- d k ^,

dk — ц = max---- 1

, и, следовательно, ц< —, и

I |U-' ^—U i^lm ’I < pr ⁵ 0. U V U! m ’I < ^1m ⁵0-

5⁰= max{5°, 50} - погрешность начального приближения. То есть необходимо выполнение неравенства

— 5⁰ 2^m

V10n²(4n²+ n)²

Так, это неравенство будет выполнено уже при

₀       25 2

m = 5log₂n + log₂5 + log₂------.

Поэтому можно утверждать о разрешимости проблемы расщепления групп векторов с одинаковыми нормами и вычислительной устойчивости алгоритма в данной ситуации.

Полученная оценка на число итераций, необходимых для эффективной работы алгоритма, получила подтверждение в ходе вычислительного эксперимента для дешифрования шифра двойной перестановки с помощью алгоритма спектрального расщепления [8]. При решении задачи проверки изоморфизма не взвешенных неориентированных графов алгоритм работает с целочисленными, за исключением диагональных элементов, матрицами. При решении задачи дешифрования шифра двойной перестановки алгоритм работает с нецелочисленными матрицами, что ведет к возрастанию погрешностей вычислений. Несмотря на это, оценка числа итераций, необходимого для приближения решений, достаточного для установления однозначного соответствия, подтвердилась.