О выводе динамически-непротиворечивой модели градиентной теории упругости методом континуализации регулярной решетки

In this paper an isotropic dynamically consistent gradient elasticity model is derived from 3D lattice. A comparison of two continualization methods is considered. Two continualization techniques are presented. First, a standard technique is applied according to which a local relation holds between the discrete and continuous variables. Secondly, use is made of a recently developed alternative continualization method, which postulates a non-local relationship between the discrete and continuous variables. The comparison has shown that the gradient elasticity model, obtained via the alternative continualization is unconditionally stable and prohibits the infinite speed of energy propagation unlike the model obtained using the classical continualiza-tion technique. Applying the alternative continualization technique, the Lagrangian density of the gradient continuum is obtained from the Lagrange function of the underlying lattice. This density is used to obtain the expressions for standard- and higher-order stresses. The equations of motion and the natural boundary conditions are derived in the Lagrangian form employing the Hamilton-Ostrogradsky variation principle.

При распространении упругих волн в материалах с микроструктурой наблюдается явление высокочастотной дисперсии, проявляющееся в зависимости фазовой скорости волн от их частоты [1]. Для описания данного явления могут использоваться либо континуальные (однородные или неоднородные), либо дискретные (решеточные) модели механического поведения материалов. Преимущество неоднородных континуальных и дискретных моделей состоит в возможности прямого моделирования микроструктуры с помощью введения зависимости свойств материала от координат. Однако численный анализ таких моделей занимает очень много времени. Вследствие этого большинство исследователей используют обобщенные однородные континуальные модели, которые способны описывать высокочастотную дисперсию упругих волн.

Одним из наиболее распространенных типов обобщенных континуумов являются так называемые градиентные континуумы, первая теория для которых была феноменологически построена в [2]. Градиентные континуумы широко используются при моделировании механических процессов в структурно-неоднородных материалах, в частности, в последнее десятилетие при моделировании дисперсии волн в структурнонеоднородных материалах [3-15]. Данная дисперсия возникает за счет рассеяния волн на структурных неоднородностях и может быть достаточно точно описана с помощью однородного градиентного континуума в случае, если длина волны, как минимум, в несколько раз превышает характерный размер неоднородности. Для достижения приемлемой точности описания, однако, модель градиентного континуума должна быть динамически непротиворечивой, т.е. устойчивой и обеспечивающей конечную скорость распространения энергии (в большинстве градиентных моделей групповая скорость волн неограниченно возрастает с частотой).

Математические модели градиентных континуумов могут быть построены несколькими способами. Наиболее распространенным является феноменологический подход, согласно которому градиентные операторы добавляются к уравнениям классического континуума исходя из общих соображений. Недостатком такого подхода является отсутствие прямой связи между микро- и макропараметрами материала. Для пре- одоления этого недостатка, необходимо выводить, а не постулировать уравнения градиентной теории. Это можно сделать, усредняя свойства неоднородного континуума или проводя континуализацию дискретной решетки.

В данной работе определяющие уравнения изотропного градиентного континуума выводятся методом континуализации уравнений движения кубической решетки, состоящей из одинаковых масс и пружин различной жесткости. Для получения динамически непротиворечивого градиентного континуума используется недавно предложенный метод континуализации [13], суть которого заключается в предположении о нелокальной связи между смещениями узлов решетки и получаемого континуума. Особое внимание в работе уделено получению выражений для классических напряжений и дополнительных градиентных напряжений, необходимых для формулировки граничных задач градиентной теории упругости.

Основные аспекты континуализации

Рассмотрим трехмерную регулярную кубическую решетку, состоящую из одинаковых частиц массой M и пружин, соединяющих эти массы. Предполагается, что каждая масса взаимодействует с 50 соседними массами (такое количество соединений необходимо для получения изотропного континуума). В состоянии равновесия массы расположены на четырех концентрических сферах, окружающих рассматриваемую массу ( m , n , k ) . На первой сфере радиусом l , равным периоду решетки, расположено 6 масс, которые соединены с центральной массой пружинами жесткости K ₁ . На второй сфере радиусом 2 l расположено 12 масс, соединенных с центральной массой пружинами жесткости K ₂ . Восемь масс, принадлежащих третьей сфере радиусом 3 l , и 24 массы, принадлежащие четвертой сфере радиусом 5 l , соединены с центральной массой пружинами жесткости K ₃ и K ₄ соответственно (рис. 1).

Рис. 1. Трехмерная кубическая решетка

Кинетическая энергия E _k ⁽ _i ^m _n ^{, n , k )} и потенциальная энергия E _p ⁽ _o ^m _t ^{, n , k )} , соответствующие массе ( m , n , k ) и пружинам, взаимодействующим с этой массой, записываются в виде

3 N

( m , n , k )                     ( m , n , k ) ² ( m , n , k )                      2

Ekin        M^V1 ^ x i       ^, E Pot         Z KK i ^ l ( i ) ^,

²    i = 1                              ² i = 1

где x ( ^m ’ ⁿ ’ ^к ) - смещение частицы ( m , n , к ) из положения равновесия, A l ₍ i ) - удлинение i -й пружины, которое легко находится геометрически, N = 50 - количество пружин, связанных с массой, K i - жесткость пружин, M - масса. Формируя функцию Лагранжа

L(m,n,k) = e(mn,k) — e(mn,k) и подставляя ее в уравнения Лагранжа второго рода, нетрудно получить уравнения движения, описывающие малые колебания массы (m, n, к) относительно состояния равновесия. Вследствие большого количества учитываемых связей данная процедура была выполнена с помощью пакета MAPLE. Получившиеся в результате три уравнения движения достаточно громоздки, поэтому ниже приводится только уравнение движения в направлении x(, дающее представление о форме уравнений движения:

Mx ( m , n , к ) _ K ( ( x ( m + 1, n , к ) _н 2 x ( m , n , к ) + x ( m ” 1, n , к ) ) + K 2 ( x ( m + 1, n + 1, к ) + x ( m + 1, n ” 1, к ) + x ( m + 1, n , к + 1)

+ x

+ x

. ( m ” 1, n , к + 1)

( m + 1, n + 1, к )

+ x

+ x

. ( m ” 1, n , к ” 1) 3

( m + 1, n , к ” 1)

( m ” 1, n , к + 1)    о  ( m , n , к )       ( m ” 1, n + 1, к )

x (            8 x (       + x (

( m ” 1, n , к ” 1)      ( m + 1, n , к + 1)      ( m ” 1, n ” 1, к )

+ x ₁         + x ₁         + x ₂

x < m + 1, n ” 1, к )

( m + 1, n , к н () x (

x m ” 1, n + 1, к )

+ x ⁽ m ^{- 1} ’ n ⁴

, к ) )

, ^K ( C( m ” 1, n + 1, к + 1)

⁺ ( ⁽ x 1

8 x ( ^m , ⁿ , ^к )

x ( m ” 1, n + 1, к + 1)

( m ” 1, n + 1, к + 1) x (

+ x ^ m н (, n н (, к + 1)

+ x ^ m ” 1, n ” 1, к + 1)

- x

+ x

+ x.

. ( m ” 1, n ” 1, к + 1) (

. ( m + 1, n ” 1, к ” 1) 1

. ( m ” 1, n + 1, к ” 1) (

x ( m + 1, n ” 1, к + 1)

x ( m + 1, n + 1, к ” 1)

+ x ( m + 1, n + 1, к + 1)

+ x

+ x.

+ x.

, ( m + 1, n ” 1, к + 1) 1

. ( m + 1, n + 1, к ” 1) • 2

. ( m + 1, n + 1, к + 1) 2

+ x.

+ x.

+ x.

. ( m + 1, n ” 1, к + 1) (

. ( m + 1, n + 1, к ” 1)

. ( m + 1, n + 1, к + 1) (

- x

+ x.

+ x.

, ( m + 1, n ” 1, к ” 1) 2

. ( m ” 1, n + 1, к ” 1) 1

. ( m ” 1, n ” 1, к ” 1) 1

x ( m + 1, n ” 1, к ” 1) x ( m ” 1, n + 1, к ” 1)

+ x 2 m н (, n н (, к

+ x ( m н (, n н (, к н () ) + ^K 4 ( x (m ” 1, n , к + 2)

(              ’ 5 V 1

40 x ₍ ^{( m} , ⁿ , ^к )

9_V ( m ” 1, n , к + 2)     ( m + 1, n , к + 2)    9 ( m + 1, n , к + 2)

2 x ₍          + x ₁          + 2 x ₍

, ...( m ” 1, n , к ” 2)    9 ( m ” 1, n , к ” 2)      ( m + 1, n , к ” 2)

+ x ₁          + 2 x ₍          + x ₁

2 x ( m + ¹ ’ n , к ” 2) + 2 x m ^{+ 2} , n ^{+ 1,} к ) + 4 x m ⁺ 2 n ^{+ 1} ’ к )

2 x 2 m + 2, n - (, к ) + 4 x ( m + 2, n ” 1, к ) + 2 x ( m + 2, n , к + 1) + 4 x< m + 2, n , к + 1) 2 x 2 m н 2, n + 1, к ) + 4 x ( m ~ 2, n + 1, к ) + 2 x 2 m ” 2, n ~ 1, к ) + 4 x ( m ~ 2, n 4, к )

+ 2 x ( ^m ” ^{2, n} , ^к ” ⁽⁾ + 4 x ^{( m} ” ^{2, n} , ^к ” ⁽⁾ + x ₍ ^{( m + 1, n} ” ^{2, к} ) ” 2 x 2 ^{m + 1, n} ” ^{2, к} ) + x + x ( m + 1, n + 2, к ) + 2 x 2 m + 1, n + 2, к ) + x ( m ” 1, n + 2, к ) _н 2 x 2 m ” 1, n + 2, к ) )

( x ( m + 2, n , к ” 1) + 4 x ( m + 2, n , к ” 1) 2 x ( m ” 2, n , к + 1) + 4 x ( m ” 2, n , к + 1) .( m ” 1, n ” 2, к ) , 9 ( m ” 1,n ” 2, к )

₁ + 2 x ₂

Для получения уравнений движения градиентного континуума необходимо аппроксимировать дифференциально-разностные уравнения движения масс решетки с помощью уравнений в частных производных. Данная процедура называется континуализацией и может быть выполнена несколькими способами. Используем сначала классический подход [16], согласно которому смещение массы ( m , n , к ) - x ^{( m} , ⁿ , ^к ) приравнивается к смещению получаемой распределенной модели u i ( x ₍, x ₂, x ₍, t ) в точке, где эта масса находится,

U i ( x ( , x 2 , x ( , t ) _ x^{( m} , ⁿ , ^к ) ( t ), i _ (,(.

Смещения окружающих масс аппроксимируются с помощью ряда Тейлора:

x⁽ m ±^A m , n ±^A n , ^к ±^{А к} ) ( t ) _ u i ( x ₍ + a ml , x ₂ ± A nl , x ₍ ± A к1 , t )

2 N 2 N ” m 2 N ” ( m + n )

= EE E ⁽± ^A ml ) ^{m (}± ^{A nl} ) ^{n (}± ^{A к1} ) ^к m = 0 n = 0     к = 0

,     д m + n + к   г             ,\

1 d u i ( x₍, x ₂, x ₍, t )

m ! n ! ^к !      d x ₍ ^m 5 x ₂ ⁿ d x ₍ ^к

+ o ( L ² N ^{+ 1})

(()

i = (,(, L = l d/ d x i <<  1.

Сходимость данного ряда гарантирована только в том случае, когда оператор L = l д/д x i является уменьшающим, что символически может быть записано в виде L <<  1. Физически данное ограничение означает, что характерные длины рассматриваемых процессов должны быть в несколько раз больше периода решетки.

Подставляя уравнения (2) и (3) в дискретные уравнения движения, получается система трех дифференциальных уравнений в частных производных. Пространственный порядок данных уравнений зависит от количества слагаемых, удерживаемых в ряде Тейлора (3), т.е. от значения N . В данной работе рассматривается континуум второго порядка, соответствующий N = 2 .

Полученные таким образом уравнения описывают анизотропный градиентный континуум второго порядка. Для того чтобы получить уравнения изотропного континуума, жесткости пружин исходной дискретной решетки должны удовлетворять определенным соотношениям. Анализ показывает, что данные соотношения имеют вид

K 1 = 4 K /3, K ₂ = 0, K ₃ = K , K ₄ = K /3.                   (4)

При выполнении условий (4) уравнения движения полученного изотропного континуума второго порядка принимают вид

Р ui , tt = ² Eu i , jj + ² u j , ij ⁾⁺ 118 El ² ( u i , jj ^{+ 4} u j , ij ) , kk ,                   ⁽⁵⁾

где u i ( x 1 , x ₂, x ₃, t ) - смещение полученного континуума в направлении x i , i , j , k = 1,3. Модуль Юнга E и плотность р в уравнении (5) связаны с параметрами решетки следующими соотношениями: M = р l ³, K = El /6 . Заметим также, что уравнение (5) описывает континуум с коэффициентом Пуассона, равным v = 1/4 .

Проанализируем уравнение (5) с точки зрения распространения волн. Для этого представим решение этого уравнения в виде плоской бегущей волны:

ui (x1,x2,x3, t) = Ui exp(i(tot - kxx - kyy - kzz)).(6)

Подставляя данное решение в уравнение (5) и вводя безразмерные волновое число K = l-^k x + k y + k Z и частоту Q = to l / c , где c = E/ р , получим дисперсионные соотношения для волн сжатия и волн сдвига соответственно:

Q, = ± — KV1080 - 250K2 , Q2 = ± — Kл]360 - 50K2 .(7)

• 1     30                        230

Дисперсионные кривые, соответствующие данным соотношениям, показаны на рис.2, а . Очевидно, что континуум, описываемый уравнением (6), описывает дисперсию волн. Однако данный континуум неустойчив относительно коротковолновых возмущений. Это следует из того, что большим действительным значениям K соответствуют мнимые частоты, одна из которых соответствует экспоненциальному росту смешений континуума во времени. Данное свойство может привести к серьезным неудобствам при исследовании переходной динамики полученного континуума. Заметим, однако, что данная неустойчивость проявляется на длинах волн, меньших периода решетки L >  1. В этом диапазоне волн полученный однородный континуум не имеет физического смысла. И все-таки уравнение (5) не может быть использовано при анализе переходных динамических процессов, т.к., строго говоря, любое возмущение будет приводить к неограниченному росту смещений континуума.

С целью преодоления данного недостатка, в работе [13] был предложен новый метод континуализации, суть которого заключается в предположении о нелокальной связи между смещениями узлов решетки и получаемого континуума. Следуя этому методу, введем нелокальное соотношение между x (m ’ n ’ k ) ( t ) и u_t ( x 1 , x ₂, x ₃, t ), предполагая, что смещение континуума u i ( x 1 , x 2 , x ₃, t ) равно среднему смещению частиц, окружающих центральную массу ( m , n , k ) :

U ( x 1 , x 2 , x 3 ,

a 1 £ x / ^сфера 1)

+ a 2 £ x ( ^{Cфера 2)}

+ a ₃ E x i ^ ³⁾

+ a ₄ £ x , ^{(cфеpа 4)}

1 + 6 a 1 + 12 a ₂ + 8 a ₃ + 24 a ₄

, (8)

где номер сферы указывает одну из четырех концентрических сфер с центром в точке ( m , n , k ) , на которой расположена масса с координатами x_i .

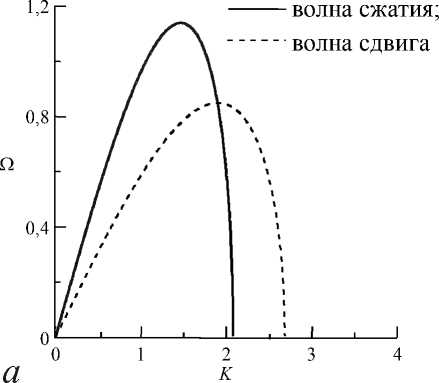
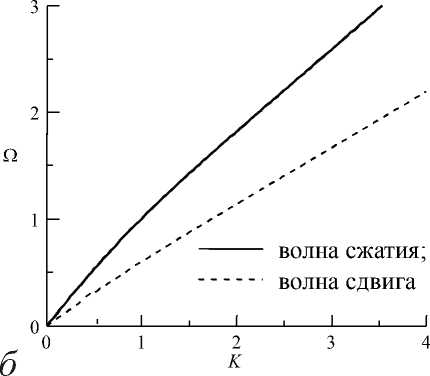
Рис.2. Дисперсионные кривые: а - для континуума, полученного стандартным методом континуализации – уравнение (5); б – для континуума, полученного новым методом континуализации – уравнение (10)

В уравнении (8) U j е [0,1), j = 1,4 - безразмерные весовые константы, которые регулируют вклад смещений масс, окружающих центральную массу, в результирующее поле смещений континуума.

Для получения уравнений движения относительно u_t ( x 1 , x ₂, x ₃, t ) все x i , входящие в уравнение (8), выразим через смещения u i и их производные. Будем предполагать при этом, что отклонение x ^{( m} ’ n ’ * ) ( t ) от u i ( x 1 , x ₂, x ₃, t ) мало настолько, что можно записать следующее соотношение:

• 2    N

^x( m , n , * ) = u i ⁽ x^ x 2 , x 3 , t ) + £ l if. ⁽ * ) ⁽ x , x 2 , x 3 , t ) + o ^{( l 2} N + 1 ) ,           ⁽⁹⁾

k = 1

где l - период решетки, N - порядок получаемого континуума, f i ( x 1 , x ₂, x ₃, t ) - неизвестные функции. Чтобы обеспечить сходимость ряда в уравнении (9), функции отклонения f_t ( x 1 , x ₂, x ₃, t ) должны удовлетворять следующему неравенству:

1 ‘ ⁺¹|У * ^{+ 1|}| <<  ql^f k *[ q <  1.

Для нахождения f_t ( x 1 , x ₂, x ₃, t ) выражения для смещений x ⁽ m ’ n ’ k ) ( t ) , определенные (9), и выражения для x (^{m +Л} m ’ n ^+л n ’ k ^{+л k} ) ( t ), которые нетрудно получить из (9) с помощью разложения в ряд Тейлора (аналогично (3)), нужно подставить в соотношение (8). Приравнивая в полученном уравнении коэффициент перед каждой степенью l к нулю отдельно, получим искомые функции отклонения f i ( x 1 , x ₂, x ₃, t ). Следует заметить, что функции отклонения f ( x 1 , x ₂, x ₃, t ) с нечетными индексами j = 1,3,5,7... обращаются в ноль, а функции отклонения с четными индексами записываются через u_i ( x 1 , x ₂, x ₃, t ) и их производные.

Теперь, зная функции f ( x 1 , x ₂, x ₃, t ), выражения для смещений x ⁽ m ^, n ^, k ) ( t ) и x *m +^л m , n +^л n , k +^л k ) ( t ) мо_Гут быть подставлены в уравнения движения для массы ( m , n , k ). В результате, учитывая соотношения между жесткостями пружин (4), получим следующее уравнение движения для изотропного континуума второго порядка:

р u_itt -р l ² Q ( u_t  ) _t1 = — E(u,  + 2 u . .)+ — El ²( u.   + 4 u . Л  - — El ² Q(u_i  + 2 u . Л , (10)

i , tt              \  i,^jj /, tt     5    \   i ^{, jj}         j,ij ,    18         \ i ^{, jj         j}kk 5               i ^{, jj j}/^k ^{v 7}

где Q = ( a 1 + 4 a ₂ + 4 a ₃ + 20 a ₄ )/( 1 + 6 a 1 + 12 a ₂ + 8 a ₃ + 24 a ₄ ) , i , j , k = 1,3 .

Дисперсионные кривые, соответствующие уравнению (10), показаны на рис. 2, б , для Q = 0.5 . Данные кривые с очевидностью показывают, что полученный континуум устойчив относительно возмущений любого пространственного масштаба (каждому действительному волновому числу соответствует действительная частота) и групповая скорость распространения волн ограничена (дисперсионные кривые стремятся к асимптоте с увеличением частоты). Посредством алгебраического анализа дисперсионного уравнения нетрудно показать, что данные свойства имеют место при 0,23 <  Q <  0,79. Параметр Q для различных параметров микроструктуры нетрудно оценить на основе общих соображений, описанных в [17].

Таким образом, градиентный континуум, полученный новым методом континуали-зации, является динамически-непротиворечивым.

Плотность функции Лагранжа и граничные условия

Уравнения (10) недостаточно для решения краевых задач теории упругости. Необходимо дополнительно сформулировать соответствующие выражения для напряжений. Наиболее удобно это сделать, используя вариационный принцип Гамильтона - Остроградского. Для применения этого принципа необходимо определить плотность функции Лагранжа Х ( x 1 , x ₂, x ₃, t ) для континуума, описываемого уравнением (10). Заметим, однако, что существует бесконечное множество выражений для плотности функции Лагранжа, соответствующих этому уравнению [18]. Поэтому, чтобы избежать неоднозначности, плотность функции Лагранжа получена в данной работе прямой континуа-лизацией функции Лагранжа решетки. Используя метод континуализации, основанный на уравнении (8), нетрудно получить следующее выражение для Х ( x 1 , x ₂, x ₃, t ):

^x = 2 р u i u i - 2 р l Qiu i ui ijj

• 1                                  \ 1,₂_

— E\u и ■ ■ + и,- u- ■ +u. и ■ I— I E(ii-

• ₅    i , j   j , i        i , j   i , j         i , i   j , j        ₉               i , jk   j , ik        i , ik   j , jk

. и.+ и. и. + и. и .+ и. и .    + 2п. и, -,) + i,jk i,kj         i,j i,jkk      vvi,j j,ikk         i,i j,jkk           i,j k,ijk *

i , j , k = 1,3 .

⁺ u i , kk u j, i ⁺ ₄ u , jj u ikk ⁺ ₂ ^u

⁺ 5 l ^{2 QE ( u}i , j u ijkk ⁺ u i , j u j jkk ⁺ ui , i u j , jkk )>

Плотность функции Лагранжа (11) зависит от производных высокого порядка и смешанных пространственно-временных производных:

^X = X ( u i , u ijk , u ij , u ijk , u ijki

i , j , k , l = 1,3.

Ниже приведены основные шаги соответствующей вариационной процедуры. Введем вариации смещений

~ i ( Х 1 , x 2 , x 3 , t ) = U i ( X 1 , x 2 , x 3 , t ) + 85 i ( x_n X 2 , X 3 , t ),

где 5 i - нормализованное возмущение, 8 - величина возмущения и предположим, что u i и ~ описывают движение континуума в промежуток времени от 1 1 до 1 ₂, так, чтобы возмущения в эти моменты времени обращались в ноль, т.е.

⁵ i ^{( x} 1 , ^x 2 , ^x 3 , t 1 ) = ⁵ i ^{( x} 1 , ^x 2 , ^x 3 , t 2 ) = °

Воспользуемся принципом Гамильтона - Остроградского, предполагая, что континуум занимает область V = {a i <  x i <  b i } с границей Г . Согласно этому принципу, для минимизации функционала действия (т.е. для получения уравнений движения и естественных граничных условий), функция Лагранжа должна удовлетворять следующему уравнению:

d

Г 1 2

d8

II ^{х dVdt}

V t1V        J

= °.

8= °

Подставляя в него плотность Х(x1, x2, x3, t), определенную выражением (11), получим t 2

2 fl дХ • и    5i +

1 1 V

V

I

дХ . дХ

Д .     5 i, jk + Д     5 i, j + д ui Jk         д ui, j

дХ

^{д u} i , jk

.     . дХ        )

5 i, jk + я       5 i, jkl д ui, jkl       J

dVdt = °.   (15)

С помощью стандартных алгебраических манипуляций это уравнение может быть приведено к виду t 2

115 '

t 1 V

Г д дХ д дХ

t 2

115 '

t 1 Г

V

Г

д t 5 U i   д x j 5 u i j

дХ д дХ

д u

' , j

д2    дХ

д ³

дХ

д ³

дХ )

^д x j ^д x k ^{s u} i. jk   ^д t ^s x j ^д x k ^дг/ ' , jk   ^д x j ^д x k ^{д x} i ^{д u} ijk J

д2   дХ

д x _k д u_ijk   S t д x _k S ti

i , jk

д2 дХ )

+-- дxk дxi Su и J

df dt -

dVdt -

t 2

t 1 Г

■ ' , j

дХ д дХ д дХ

д u _jk

' , jk

^д t ^{д u} i , jk   ^д x l ^{д u} iJkl J

dГdt -

f s дХ

^{1 5} ' S u , ^{+ 5}

дХ

t 2

V

I

'j д u,«

' , jk

t 1

t 2

^dV - Jf 5 i , jk -г— d r dt = °.

1 1 Г         ^{д u} i , jkl

Приравнивая к нулю подынтегральное выражение первого интеграла в уравнении (16), получим уравнения движения континуума в форме Лагранжа:

д дХ д дХ---1--- дt дUi дxj дui j

н

д2    дХ

д ³

дХ

д ³

дХ

---1----1--- дxjaxk au',jk   ataxjдxk дut,jk   дxjдxkдxi дu,jki

= °.    (17)

Нетрудно проверить, что ранее полученное уравнение движения (10) может быть получено прямой подстановкой плотности функции Лагранжа (11) в уравнение (17).

Из второго и третьего интегралов получаем естественные граничные условия:

о = ^σ ij

∂λ

∂ u i , j

∂ ∂λ     ∂2   ∂λ ∂2 ∂λ+-   -   ,

∂ x_k ∂ u_{i , jk}   ∂ t ∂ x_k ∂ u_{i , jk}   ∂ x_k ∂ x_l ∂ u_{i , jkl}

∂λ ∂ ∂λ ∂ ∂λ

++  ,

^{∂ u} i , jk    ^{∂ t ∂ u} i , jk    ^{∂ x} l ^{∂ u} i , jkl

где σ _ij и τ _ijk имеют смысл классических и градиентных напряжений. Подставляя λ в выражения (18) и (19), нетрудно выразить данные напряжения через смещения континуума:

1 2           2                                1       2

^c ij = 2 ^р l Qu i,j + 5 E ( ^u j , i + u , j + ^u k , k ⁵ j ) - 5 EQl (2^ui , jkk + ^{2 u} j , ikk + 2 u k , k_U 5 j ) +

⁺ ₁₈ ^{El (2 u} j , ikk ^{+ u} i , jkk ^{+ 2 u} k , ijk ^),

T jk =- 1 P Ql ² u^_jk + ¹ EQl ²( u_1Jk + U jik + U m , mk 5 j ) + -1- El ²( - 2 U jik + 2 u, , Ik 5 j +

2            5                             18

^{+ 2 u} j , ll ^δ ik ^{+ 2 u}l , il ^δ jk ^{+ u}i , ll ^δ jk ^).

Зная выражения для напряжений, математическая модель, полученная в данной работе, может быть применена для решения краевых задач, связанных с анализом динамического поведения материалов с микроструктурой.