О выводе и вычислении функционалов в нелинейных статистических краевых задачах механики композитов

В работе [1] устанавливается важное свойство микронеоднородных квазиизотропных тел, когда моделью сравнения является однородная сплошная среда с осредненными свойствами:

^£ j = ^O ij «Р^ e ap ’                         ⁽¹⁾

где £ j ( r ) - структурные деформации микронеоднородной среды; e j = (^£ iA — макроскопические деформации микронеоднородной среды; ^ ijmn ( r ) — случайные модули упругости микронеоднородной среды; O j _а р (0) - случайный функционал, зависящий от упругих свойств микронеоднородной среды.

В работе [2] указан метод вычисления моментов различных порядков функционала Ф ij _а р ( 0 ) , позволяющий вычислять как эффективные свойства микронеоднородной среды, так и структурные поля деформирования. На основе полученного решения устанавливается важное свойство микронеоднородной среды: если упругие свойства микронеоднородной среды являются локально-эргодическими, то и поля деформирования микронеоднородной среды являются локально-эргодическими.

В работе [3] дается обобщение соотношения (1) на микронеодно-родные тела, когда моделью сравнения является микронеоднородная среда с регулярной структурой. Если микронеоднородная среда макро- скопически однородна и макроанизотропна, перемещения границы тела, имеющего конечные размеры, детерминированы, дисперсии физических свойств среды конечны, микродеформации регулярной среды в пределах структурного элемента - гладкие функции координат, то существует случайный функционал Ф(р)(0), не зависящий от граничных условий, такой, что пульсации структурных деформаций е (r) связаны со структурными деформациями в регулярной среде е( p) (r) соотношением е (r) = Ф(p^б)^p^r). (2) В этой же работе приводится общий метод вычисления функционала ф( p)(6) для микронеоднородных сред. Соотношение (2) позволяет получить более точные формулы для расчета эффективных свойств композитов. Для макроскопически однородной квазиизотропной среды в корреляционном приближении получаем следующие зависимости:

* ^ tjmn

^{( p )} *        °      °       \

Ctjmn ^    tjy8v аРmn JJ уабр , где C*jmn - эффективные модули упругости композита; C^n* - макро скопические модули упругости регулярной среды сравнения; J*а8р -изотропный тензор четвертого ранга, зависящий от макроскопических модулей неоднородной среды сравнения с периодической структурой.

Аналогичные зависимости получаем для эффективных модулей упругости квазиизотропных композитов с учетом конечных дисперсий физических свойств среды:

*           ⁽ р ⁾*         °      °         \ ,*

C tjmn C tjmn ^ \ tj уб ° аД mn ]^J уа ₁ 8р ₁ ^ ’” ^

°       °            °                  °                *         *               *

ij У ⁸° ^а 1 ^р 1 У 1 ⁸ 1 ° ^а 2 ^р 2 У 2 ^б 2^," ° ^а к ^р k ^mn[^J У ^а 1 ^8р 1 J У 1 ^а 2 ^б 1 ^р 2" ' J У к - 1 ^а 2 ⁸ к - 1 ^р к ⁺ ’”

Соотношение (3) представляет собой решение задачи, если соответствующие ряды сходятся. Сходимость рядов в каждом конкретном случае устанавливается непосредственной проверкой при заданных свойствах структурных компонентов [1].

Перейдем теперь к вычислению моментных функций второго порядка структурных деформаций. Перемножив уравнение (2), взятое относительно двух произвольно выбранных точек трехмерного пространства и применив оператор математического ожидания, находим моментную функцию второго порядка структурных деформаций:

L ijmn ( r l r ₂) = F j ^rO ^ yS\ r ₂) , ⁽⁴⁾ где через L_jmn ( r _l , r ₂ ) = ^£ ° _j ( r _l ) e ° _mn ( r ₂ )^ обозначена моментная функция второго порядка структурных деформаций; F mnqs = ^Ф^Ф ^Т Х) — коэффициенты, зависящие только от физических свойств элементов структуры.

Для квазиизотропной среды эти коэффициенты вычисляются в явном виде. Тогда из уравнения (4) получаем явные аналитические зависимости для моментных функций второго порядка структурных деформаций:

L jmn ( r ' . r" ) = J j J, *, K S" ( r ' . И ^ ( r ' ) = !" ( r" ) , (5)

где K ^p" ( r ' , r '' ) — моментная функция второго порядка структурных модулей упругости:

K S" ( r ' , r- ) =(e -_NpP ( r ' , r- ) e - _T5aP ( r ' , r- )) . (6) Если поля упругих свойств микронеоднородной среды (6) являются локально-эргодическими, то и поля структурных деформаций, как следует из формулы (5), также являются локально-эргодическими.

Для описания структурного разрушения и прогнозирования прочностных свойств композитов в определяющие соотношения вводится новый материальный носитель ® j _mn ( = h ) , зависящий от условий нагружения [4]. Таким образом, в качестве математической модели процесса квазистатического деформирования и разрушения в рамках такого подхода может быть поставлена стохастическая краевая задача механики композитов [4]:

V -o ( r ) = 0 , e( r ) = def u ( r ), o ( r ) = C : [ I - © ( « ) ] : = , u ( r )| ₅ = = * • r , (7) где C - тензор модулей упругости изотропной сплошной среды; I -единичный тензор четвертого ранга; = * - заданный тензор макродеформаций; u ( r ) - тензор структурных перемещений.

Для замыкания системы уравнений (7) необходимо дополнить ее уравнениями для определения го ( r ) . Будем предполагать, что заданы явные зависимости

ГО (г) = ГО (£h ) , где £h (r) - инварианты тензора структурных деформаций.

Наложим на случайное поле го ( г ) математические ограничения общего характера в виде локально-статистической однородности и локальной эргодичности.

Случайное поле го ( r ) есть локально-статистически однородное поле, если многоточечный закон распределения f ^ n ⁾ ( r 1 , r ₂,..., r n ) , n = 1, 2, 3,... не изменяется после параллельного переноса точек M 1 ( r ) , M ₂ ( r ₂ ) ,..., M n ( r n ) на равные расстояния, не превышающие характерного размера некоторой области статистической зависимости V * с V . Под областью V * понимается шар, радиус которого равен г² 1 , 0 < £ << 1, 1 - характерный размер конструкции.

Случайное поле го ( r ) есть локально-эргодическое поле если го ( r ) локально-статистически однородно и моментные функции произвольного порядка к финитны в области V * с V , т.е.

K » ( r l , ^r 2 ^,-^{, r} k ) = (^го ° ( ^r 1 ) ^го ° ( ^r 2 ) -^го° ( r k )) =

* ^т < D

= 0,^ > D, к = 2,3, rm = max

|r i - r j , i , j = 1, к , D - характерный размер области V *.

Сформулируем свойство микронеоднородных сред аналогично свойству (1). Если микронеоднородная среда с однородными упругими и неоднородными прочностными свойствами макроскопически однородна и квазиизотропна, поля структурных повреждений при деформировании локально-эргодические, средние деформации макроскопически гладкие функции координат, граничные условия детерминированы, то существует случайный функционал Ф ^р ( го ) , зависящий только от поля структурных повреждений, такой, что пульсации структурных деформаций £ ° связаны со средними деформациями e ( r ) в регулярной среде сравнения соотношениями:

£ ° ( r ) = Ф ^{( р )}( го ) : e ( r ) . (8) Доказательство соотношения (8) аналогично доказательству соотношения (1).

Из соотношения (8) вытекает, что если поля структурных повреждений локально-эргодические, то и поля деформирования тоже являются локально-эргодическими. Как показывают прямые численные эксперименты [5, 6], локальность полей структурных повреждений имеет место на стадии дисперсного накопления повреждений, что является признаком ближнего порядка во взаимодействии полей микродеформаций и структурных повреждений на начальном этапе структурного разрушения. Дальнейшее увеличение нагрузки приводит к укрупнению дефектов и местной локализации повреждений.

Рассмотрим теперь более общий случай, когда поля упругих свойств 6 ( r ) и структурных повреждений to ( r ) являются локально-эргодическими. Будем также предполагать, что эти поля являются собственными, т.е. отсутствует взаимная корреляция между полями:

( 6 ( r ) to ( r )) = 0 .

Сформулируем свойство микронеоднородных сред, аналогичное свойству (2). Если микронеоднородная среда с неоднородными упругими и неоднородными прочностными свойствами макроскопически однородна и квазиизотропна, поля структурных повреждений при деформировании локально-эргодические, структурные деформации в периодической среде сравнения в пределах упругого элемента - гладкие функции координат, граничные условия детерминированы, то существует случайный функционал Ф ^р ( 6 , to ) , зависящий от полей упругих свойств и структурных повреждений, такой, что пульсации структурных деформаций £ ° связаны со структурными деформациями £ ^{( р )} ( r ) в регулярной среде сравнения соотношениями:

£ ° ( r ) = Ф ^{( р )}( 6 , to ) : £ ^{( р )}( r ) . (9)

Для доказательства формулы (9) рассмотрим стохастическую краевую задачу механики микронеоднородных сред в отсутствии объемных сил:

V- o ( r ) = 0 , £ ( r ) = def u ( r ) , о ( r ) = 0 ( r ) : [ j - to ( £ ) ] : £ ( r ) , to ( r ) = to ( £ )                                  (10)

с условиями специального вида dV J £(r)dV = £', dIV которые, как известно [4], эквивалентны условиям на поверхности S тела V:

^{u ( r )}|

*

S = 8 • ^r .

при макроскопически однородном деформированном состоянии.

Идея излагаемого ниже метода заключается в использовании в качестве основы решения аналогичной краевой задачи для среды с регулярной микроструктурой:

V -о(p)(r) = 0, £(p) (r) = def u(p) (r), o(p) (r) = C(p) (r): £(p) (r), dV J£p)(r)dV = E-, dIV где u(p)(r), £(p)(r), o(p)(r) - детерминированные периодические функции структурных перемещений, деформаций и напряжений, C( p) (r) -тензор структурных модулей упругости среды с регулярной структурой. Предположим, что решение краевой задачи (4) нам известно [7]:

£(p) (r ) = N(p) (r ) : £* , £(p) (r ) = £* + £(p) ( r ) ,C-^ >=Ге< p '( r )Mdp'( r): n(p >(r)

, И ^{p )} = C ^{-( p )} £ ^- ,

где C * ⁽ p ⁾ - эффективные модули упругости среды с регулярной структурой; N ^{( p )} ( r ) - структурные функции [7]; [...] - оператор осреднения по представительному объему.

С целью доказательства соотношения (9) исследуем решение краевой задачи (10) с граничными условиями (11), которая приводится к интегрированию системы дифференциальных уравнений при нулевых граничных условиях:

V- (C(p): def u° ) = -V- П, u°| s = 0, где

П = 0 ° def u ^{( p} U 0 ° : def u " - (6 ° : def u °),

/^/

6 °.

ijmn

t*''

6 °-..

ijmn

?*^

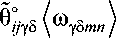
" Уч"

^ ij /8 ^ /8 mn ^

^ ij /8 L I /8 mn  ^ /8 mn

0..

ijmn

Уравнения (12) можно рассматривать как уравнения краевой задачи теории упругости микронеоднородных сред с регулярной структурой C ^{( p )} ( r ) и перемещениями u ° ( r ) , обусловленными действием фиктивных случайных объемных сил V • П .

При введении функции Грина среды с регулярной структурой G ^{( p )} ( r , r ' ) система дифференциальных уравнений (12) преобразуется в систему интегро-дифференциальных уравнений:

u ° ( r ) = j G ^{( p )} ( r , r ' ) - L V- П ( r ' ) ] dV '                 (13)

V

Для определения полей структурных деформаций необходимо знать градиент пульсаций структурных перемещений, поэтому дифференцируем (6):

V u ° ( r ) = j v G ^{( p )} ( r , r ' ) - L v- П ( r ' ) ] dV '.              (14)

V

Уравнение (13) решаем методом последовательных приближений при ограничениях, сформулированных в виде макроскопической однородности и квазиизотропности микронеоднородной среды.

В первом приближений полагаем:

V u ° ₁₎ ( r ) = j V G ^{( p )} • V • ( 0 ° : е ^{( p )} ) dV

V

Для макроскопически однородной среды интегралы в выражение (15) фактически распространяются на a ² f -окрестность микронеоднородной среды, где е( ^р ) - постоянны, поэтому соотношения (15) принимают вид:

V u- , ( r ) V p : , ' /: _Е^{( p 1} ,

где Vp(1p)) = j*VG(p)(r,r')(V'-0°)dV*, а Vp(^ (б°,r) тензор-функционал V третьего ранга относительно физических свойств микронеоднородной среды.

Подставляя (15) в (14), с учетом (16) получаем второе приближение:

V u ° 2 , ( r I ( V p    -V p )_: £ ^p I ,

V p ( p ’ = J v G ^{( p 1} (V' ( 0 ° :V p ^{( p )} ) dV' .

V

Окончательно запишем:

Vu° (r ) = Vp(p 1: £(p 1,

»

^V p ^{( p 1} = £ v p ( ,’ ) .

к = 1

Поскольку пульсации структурных деформаций определяются выражением

£° (r) = def u° (r), то в силу (17) приходим к соотношению (9):

£ (r ) = Ф(Р1 (0, ГО) : £(р 1 (r), где функционал Ф(p 1 (0, го) определяется уравнением:

Ф ^{( p 1} ( 0 , го ) = def p ^{( p 1} ( 0 , го ) .

В первом (корреляционном) приближении эти функционалы определяются следующими соотношениями:

ф ( Р ) =1 ijmn ₂

i f a p(p 1 a^ _ г imn ^

.(.p1 ) jmn

5х=

V ^j

5х, i J

,

5p ( pn    Г ⁵ GL^P ' ( r . r ' )

⁵ x

V

5 X j      5 X p'

Sipmn ( r') dv',

где G j ' ( r , r ' ) - тензорная функция Грина для периодической среды сравнения с неоднородными свойствами.

Из соотношения (18) следует, что указанные выше функционалы являются функционалами относительно свойств микронеоднородной среды Q _jjmn ( г ) и тензора микроповреждаемости to _ijmn , а также функциями относительно текущей координаты г . Из уравнения (10) следу- ( р ) ет, что моментная функция второго порядка функционала Ф^ П однозначно определяется через моментную функцию второго порядка ( р )

функционала р m j , где через запятую обозначается дифференцирование по координате X j . Следовательно, для вычисления моментной функции второго порядка необходимо вычислить двойной интеграл

F pjm ( г , г ' ) -

йр ip (г) »%(г*) _

aх,       axn jq

“Jf

V

aG' )(г, г’) aG«( r', ф2кф (г-, г-)     , d v d v ,

axf          axn jq

Й X p 5 X 5

где через K^ (г-, г")-(бjm„ (И^ (г")) обозначена структурная моментная функция второго порядка свойств микронеоднородной среды. Как показывают многочисленные теоретические и экспериментальные исследования, эта функция локальна (затухает на расстояниях намного меньших линейного размера элемента) и имеет область отрицательных значений [1, 4]. Для корреляционной функции, входящей в соотношение (19), используются аппроксимирующие зависимости через единичные функции, предложенные в [1]. Тогда для описания функции F^n (г, г') достаточно вычислить некоторые значения этой функции, получаемые при г - г* - 0 в уравнении (19). Для вычисления интеграла (25) необходимо знать функцию Грина Gj)(г, г’) для неоднородной среды сравнения с периодической структурой. Используя технику осреднения, предложенную в работе [3], представим функцию Грина Gj)(0, ^;0, г) в виде асимптотического ряда разложения по ма лому параметру а:

GрI (0,fc0,Г) = G* (r)+aA^ (%)^r)+

°x Y 1

°² G aB ( Г )