О взаимодействиии вращающихся тел

Дано объяснение экспериментальных фактов, свидетельствующих о взаимодействии вращающихся масс, с позиций энергодинамики. Показано, что это взаимодействие не сводимо к известным четырем его видам и обусловлено неравномерным распределением в пространстве момента импульса. Получено выражение для расчета торсионной силы

Оглавление

• 1.    Экспериментальные факты

• 2.    Теория Литература

1.    Экспериментальные факты

В опубликованных материалах неоднократно приводились факты, убедительно свидетельствующие о взаимодействии вращающихся тел друг с другом и с окружающими их неподвижными телами. Одним из первых свидетельств такого рода являлся индикатор Мышкина, построенный им в начале ХХ столетия и реагировавший на вращение находящегося вне его гироскопа [1]. Этот индикатор представлял собой стеклянный сосуд с подвешенным в нем на тонкой нити (или паутине) диском диаметром 30-40 мм. из алюминиевой фольги. При раскрутке рядом расположенного гироскопа диск индикатора медленно отклонялся от своего первоначального положения на некоторый угол и находился в этом положении до тех пор, пока длился опыт. После отключения гироскопа диск медленно возвращался в исходное положение [1].

Одним из первых «гироскопический эффект», заключающийся в уменьшении веса вращающихся гироскопов, наблюдал Н.

Козырев [2]. В его опытах изменение веса гироскопа происходило вдоль оси вращения массы, причем в зависимости от направления вращения гироскопа происходило либо уменьшение, либо увеличение его веса.

Проявления взаимодействия вращающихся масс в макромире многообразны. Один из них – эффект возникновения «гироскопической тяги» –демонстировался еще в 1974 году Э. Лэйтвэйтом (Eric Laithwaite) во время его знаменитой рождественской лекции в Королевском Институте Великобритании [3]. В этом опыте раскрученный гироскоп весом 10 кг подвешивался за один из концов ротора к вертикальной струне и, будучи отпущенным, приходил к движению по спирали, вызывая отклонение подвеса от вертикали.

Другой эффект – кажущееся «обезвешивание» вращающихся масс. В этом отношении заслуживают внимания прецизионные измерения веса вращающихся гироскопов, выполненные в 1989 году японскими физиками Х. Хидео Хайасака и С. Такеучи [4]. Их исследования показали, что при скоростях (12-13)·103 об/мин 175граммовый гироскоп теряет в весе до 10 миллиграмм. Кроме того, они установили, что горизонтально вращающийся ротор легче неподвижного, а вращающийся по часовой стрелке легче вращающегося против часовой на величину порядка 7·10-8 % [4]. Сами исследователи не смогли объяснить причину такого эффекта. Тем не менее они заявили о теоретической возможности получения «антигравитации» и полного нарушения притяжения. Эти выводы, по их мнению, следуют из результатов экспериментов по свободному падению гироскопов, которые были осуществлены другими японскими физиками Х. Танакой, Т. Хашидом и Т. Щубачи.

Еще один эффект был обнаружен в экспериментах Е. Подклетнова [5], наблюдавшего уменьшение веса предмета, расположенного над сверхпроводящим вращающимся диском, находящимся в магнитном поле.

Наиболее впечатляющими в отношении уменьшения веса явились эксперименты В. Рощина и С. Година на установке массой 350 кг., названной ими электромагнитным конвертором [6]. При раскрутке ротора конвертора внешним электродвигателем наблюдалось уменьшение его веса по показаниям пружинных весов на 35...50% . При наступлении резонансного режима (при числе оборотов порядка 500...600 об/мин.) они наблюдали также проявление «эффекта Сёрла» – самопроизвольное ускорение ротора

Доклады независимых авторов 2012 выпуск 21 с расположенными по его периферии роликообразных постоянных магнитов после отключения разгонного электродвигателя. Однако столь значительная потеря веса объясняется скорее всего смещением ротора по вертикали в новое равновесное положение без потери его веса, возможность чего будет показана ниже.

Подтверждением многообразия проявлений взаимодействия вращающихся тел с их окружением служат также эксперименты А.Л. Дмитриева с сотрудниками, результаты которых впервые были опубликованы в 2001 г. [7]. В их установке в закрытый контейнер помещались два соосных гироскопа с горизонтальной осью вращения. В экспериментах измерялось ускорение свободного падения контейнера, для чего на нем был закреплен высокостабильный генератор импульсов длительностью 0,13 мс, подключенный к двум разноцветным светодиодам, расположенным вдоль траектории падения контейнера. Траектория падающего контейнера фотографировалась цифровой камерой с выдержкой 0,5-0.6 с., которая засекала координаты центров диафрагм, установленных перед светодиодами с последующей оцифровкой результатов на компьютере. Для уменьшения влияния искажений изображения вследствие дисторсии средний масштаб изображения рассчитывался по трем отсчетам длины - в верхней, центральной и нижней частях траектории. Эти эксперименты показали, что при угловой скорости вращения гироскопов 20 000 об/мин наблюдалось систематическое увеличение ускорения свободного падения контейнера величиной 10 ± 2 см/с2.

Весьма детальные исследования взаимодействия вращающихся масс выполнил С.В. Плотников [8]. В его экспериментах стандартный гироскоп авиационного автопилота массой 540 грамм жестко крепился на чаше аналитических весов класса АДВ-200М, причем для компенсации его веса была предусмотрена его пружинная подвеска. Питание гироскопа осуществлялось напряжением 12 вольт через 3-х фазный преобразователь на 400В, который предусматривал возможность плавного изменения скорости до 20·10³ об/мин с переключением направления вращения. Результаты эксперимента показаны на рис. 1.

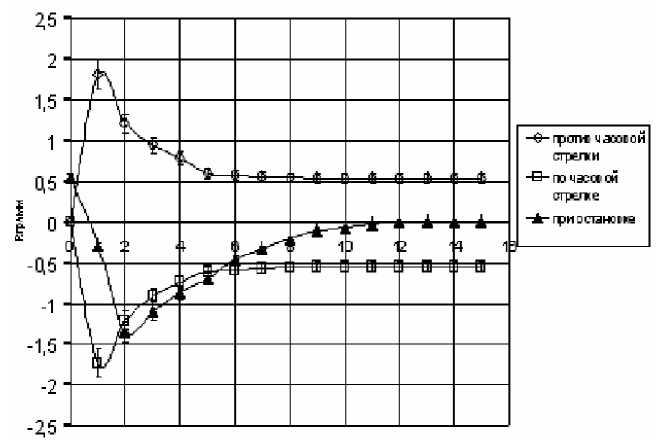
Рис.1. Зависимость веса гироскопа от времени

Как следует из рисунка, при вращении гироскопа по часовой стрелке (совпадающем с направлением вращения Земли) вес гироскопа увеличивается, а при его вращении против часовой стрелки, наоборот, уменьшается. При этом наиболее резкое изменение веса происходит в процессе раскрутки гироскопа. Затем по мере набора оборотов величина эффекта плавно снижается и принимает стационарное значение, изменяющееся с изменением напряжения питания от 12 до 15 В от 430 мг до 540мг. При подвесе гироскопа перпендикулярно весам наблюдается аналогичное изменение веса, но стационарное значение оказывается меньшим и равным 280 мг. Аналогичная картина наблюдается и при отключении питания гироскопа. При этом вес его резко уменьшается и затем плавно восстанавливается.

Аналогичные эксперименты были проведены Плотниковым для взаимодействия двух гироскопов, второй из которых подвешивался к потолку на удалении 3 см. от центра масс первого. При вращении гироскопов в одном направлении вес 1-го из них увеличивался на 150 мг., изменяя знак при вращении в противоположные стороны. При перпендикулярном расположении осей гироскопов изменения веса гироскопа не наблюдалось.

Серию исследований взаимодействия близкорасположенных вращающихся дисков в вакууме выполнил В.Н. Самохвалов [9]. В его установке на роторах двух соосных электродвигателей постоянного тока закреплялись два алюминиевых диска диаметром

Доклады независимых авторов 2012 выпуск 21 165 мм. Верхний диск был подвешен к ротору электродвигателя на нитях, нижний диск – жестко закреплен на фланце ротора другого электродвигателя. Зазор между дисками составлял 2-3 мм. При раскрутке нижнего диска помимо их нагрева наблюдалось вынужденное вращение верхнего незаторможенного диска, механически с ним не связанного. При этом частота этого вращения на воздухе при прочих равных условиях была на два порядка ниже, чем при вращении дисков в вакууме. Если же верхний диск был заторможен, наблюдался его подъем вследствие отталкивания вращающимся диском. То же самое отталкивание происходило и с другими близкорасположенными неподвижными предметами, например, рычагами. Эти эффекты не зависели от материала дисков, что доказывало неэлектромагнитную природу данного взаимодействия. Попытки обнаружить возникновение электрического поля вблизи торцов дисков при их вращении также оказались безуспешными. Экспериментатор приписывает этот эффект некоторому «квадрупольному излучению».

Весьма важную информацию о эффекте гироскопической тяги дает эксперимент канадского исследователя Г.А. Голушко [10], являющийся повторением упомянутого выше опыта Эрика Лэйтвэйта. Экспериментальная установка представляла собой раскручиваемый вручную гироскоп массой М = 98 г., подвешенный на нити длиной l = 224 см и снабженный лазерной указкой, оставлявшей световое пятно на горизонтально расположенном линованом листе бумаги. В отличие от установки Лэйтвэйта, гироскоп был изолирован от окружающего воздуха бумажными экранами конической формы. На одном из концов оси гироскопа была закреплена стрелка-указатель, предназначенная для определения ориентации оси гироскопа. Положение светового пятна и стрелки-указателя отслеживается с помощью видеосъёмки, проводимой с двух ракурсов: сверху и сбоку. Благодаря этому автору удалось произвести измерение траектории движения гироскопа, обусловленной тягой гироскопа, и ориентации его оси относительно нормали к траектории (рис.2). В результате экспериментов было установлено, что гироскоп представляет собой незамкнутую систему, вектор тяги которой направлен вдоль оси гироскопа.

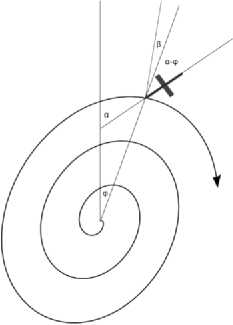
Рис.2. Траектория раскрутки гироскопа

Этот эксперимент обнаружил волнообразный характер изменения отклонения подвеса от вертикали, обусловленный изменением направления вектора гироскопической тяги (ускорением и замедлением движения гироскопа). При разгоне ось гироскопа и вектор его тяги ориентированы в сторону движения. Однако по мере увеличения угловой скорости ось гироскопа начинает «отставать», и вектор тяги поворачивается в сторону, противоположную движению. В результате торможении угловая скорость движения гироскопа уменьшается, и «отстаёт» груз. Это повторяется многократно, что и обусловливает волнообразный характер его движения по спирали. Характерно, что при симметричной подвеске корпуса гироскопа, когда оба конца его ротора вращаются свободно, среднее отклонение его от вертикали равно нулю.

Объяснения, даваемые авторами этого и других упомянутых здесь экспериментов, выходят за рамки существующих теорий. Единственной на сегодняшний день теорией, из которой существование специфического «торсионного» взаимодействия вытекает без каких-либо дополнительных гипотез, является энергодинамика. Покажем это по возможности кратко.

2.    Теория

Существование специфического, не сводимого к другим взаимодействия между вращающимися телами или телом и окружающей его средой, непосредственно вытекает из энергодинамики, обобщающей термодинамику на пространственно неоднородные системы и нетепловые формы движения [11]. Эта теория рассматривает в качестве объекта исследования всю совокупность взаимодействующих (взаимно движущихся) тел или частей системы, рассматривая её как единое неравновесное целое. Основное уравнение энергодинамики таких систем учитывает все протекающие в них процессы и имеет вид тождества:

dE ≡ Σ i Ψ i d Θ i – Σ i F i · d r i – Σ i М i · d φ i ,                 (1)

где E – полная энергия системы; Θ _i – обобщенные координаты состояния системы: её объема V , энтропия S , масса m , числа молей k -х вещества N k , заряд З , компоненты Р _α импульса системы Р , компоненты L _α его момента L _α (α = 1,2,3) и т.д.; Ψ _i ≡ ( ∂Е / ∂ Θ _i ) – обобщенные потенциалы системы типа абсолютного давления р и температуры Т , энтальпии h и химических потенциалов k -x веществ μ k , электрического потенциала φ, компоненты v_α и ω_α векторов скорости поступательного и вращательного движения v и ω и т.д.; F _i ≡ – ( ∂Е / ∂ r _i ) М _i ≡ – ( ∂U / ∂ φ _i ) силы в их обычном (ньютоновском) понимании; М _i ≡ – ( ∂Е / ∂ φ _i ) – их крутящие моменты; i = 1, 2,…, n – число составляющих энергии системы.

В этом выражении члены первой суммы характеризуют работу объемной деформации системы как целого, теплобмен и массообмен её с окружающей средой, диффузию k -x веществ через её границы, электризацию системы, поступательное и вращательное ускорение её как целого и т.д., т.е. воздействия, не нарушающие внутреннего равновесия в системе. Вторая сумма этого выражения, напротив, характеризует работу, совершаемую внешними или внутренними силами F _i против равновесия в ней. Эта работа связана с перераспределением параметров Θ _i по объему системы V и смещением центра их величины на расстояние d r _i . Наконец, третья сумма (1), интересующая нас более всего, характеризует работу, совершаемую внешними или внутренними крутящими моментами при переориентации системы во внешних полях (её повороте на пространственный угол φ _i

При таком подходе (от целого к части) несложно убедиться в противоположной направленности процессов, протекающих в отдельных частях такой системы. Например, представляя модуль L _ω момента импульса системы L _ω = r×Р в виде интеграла от его плотности ρ_ω по объему V системы L _ω = ∫ρ_ω dV , а затем выражая ту же величину через среднее значение ρ_ωо этой плотности L _ω = ∫ρ_ωо dV , находим, что производная по времени t от выражения ∫(ρ_ω – ρ_ωо) dV тождественно равна нулю:

∫[ d (ρ ω – ρ ωо )/ dt ] dV = 0 .                               (2)

Равенство этого интеграла нулю возможно в двух случаях: когда производные d (ρ_ω– ρ_ωо)/ dt во всех точках объема системы равны нулю (т.е. никаких процессов в системе не происходит), и когда хотя бы часть этих величин имеет противоположный знак, взаимно компенсируясь. Таким образом, внутри неоднородной системы всегда протекают противонаправленные процессы. Например, при раскрутке гироскопа, подвешенного за один конец ротора) до скорости ω остальная часть системы приобретает равный по величине, но обратный по знаку момент импульса L _ω. Его наличие может быть незаметным на глаз, если момент инерции этой части I _ω намного больше момента инерции гироскопа I _ωг, однако в силу закона сохранения I _ω отличен от нуля. Это лишает всякого основания утверждения об отсутствии реакции на раскрутку гироскопа со стороны окружающей его среды.

Если величина момента импульса L _ω распределена по объему системы неравномерно, положение центра её величины (её радиус-вектор r _i ) определяется известными выражениями:

rω = Lω-1 ∫ ρω(r,t)rdV , (3)

где ρ_ω( r , t ) – плотность момента импульса в точке поля с координатой r .

Сопоставляя эту величину с радиус вектором r _ωо= L _ω^-1 ∫ ρ_ωо( t ) r dV той же величины L _ω в однородном состоянии с плотностью ρ_ωо( t ), найдем, что в системе с неоднородным «полем завихренности» происходит смещение центра величины L _ω от его равновесного положения на расстояние ∆ r _ω = r _ω– r _ωо, в связи с чем возникает некоторый «момент распределения» этой величины [11]:

Zω = Lω∆rω = ∫ [ρω(r,t) – ρωо(t)]rdV . (4)

Поскольку фактически Lω – вектор, нормальный к направлению к вектору смещения ∆rω, момент Zω выражается векторным произведением ∆rω×Lω и потому направлен в ту же сторону, что и крутящий момент Мω. Он характеризует удаление системы от состояния «однородной завихренности», т.е. служит мерой неоднородности поля угловых скоростей в ней и является одним из параметров пространственной неоднородности системы. Число таких параметров в общем случае равно числу составляющих энергии системы, неравномерное распределение которых они и характеризуют. Отличие Zω и Мω от нуля свидетельствует о том, что кинетическая энергия вращения Еω зависит не только от величины момента инерции Lω, но и от его положения в пространстве rω, как и любые другие составляющие внешней энергии. Наличие градиента энергии вращения порождает некоторую силу Fω в её обычном (ньютоновском) понимании, которая стремится возвратить систему в исходное (равновесное) состояние с Zω = 0. В энергодинамике эта сила, которую мы для краткости будем называть гироскопической, определяется так же, как и для потенциальных форм энергии, т.е. как взятая с обратным знаком производная от энергии рассматриваемой системы Е по её пространственной координате rω :

Fω ≡ – (∂Е/∂rω). (5)

Таким образом, мы приходим к заключению о существовании в неравномерно вращающихся средах ещё одного вида взаимодействия, не сводимого к 4-м известным его видам (сильному, слабому, электромагнитному и гравитационному).

Обратимся теперь к членам 3-й суммы (1) и рассмотрим случай, связанный с вращением частей системы с угловой скоростью ω = d φ/ dt. Величину вращающего момента М _ω в этом процессе можно найти по мощности этого процесса N _ω = dE _φ ^k/ dt = I ω( d ω / dt ) = М _ωω, откуда следует эйлеровское выражение ускоряющего момента М _ω = Id ω / dt , аналогичное закону Ньютона для поступательного ускорения F = md v / dt. В системах с неоднородной завихренностью угловая скорость зависит от координаты поля r и времени t , т.е. ω = ω( r , t ), и её полная производная по времени определяется выражением

dω/dt = (dω/dt)r +(v·∇)ω . (6)

Описываемое этой формулой угловое ускорение включает наряду с локальной составляющей углового ускорения ( d ω / dt ) _r так называемую конвективную составляющую М _ω^k, характеризующую ускорение, связанное с перемещением вращающегося тела в поле завихренности с градиентом угловой скорости ∇ ω. Эта составляющая крутящего момента определяется выражением

Мωk= Iv·∇ω , (7)

что свидетельствует о существовании в природе еще одного вида силового взаимодействия, осуществляемого переносом частицами вещества вихревого движения. Это явление, изучаемое в гидро-и аэродинамике, может иметь место и в эфире, что и обнаруживают, по-видимому, упомянутые выше эксперименты Самохвалова.

Таким образом, экспериментально наблюдаемые явления возникновения гироскопической силы и передачи вращательного движения от одних тел к другим вытекают из энергодинамики без каких-либо дополнительных гипотез и постулатов.