О взаимосвязи между упругими и тепловыми характеристиками твердых тел

Автор: Сандитов Д.С., Цыденова Д.Н., Дармаев М.В., Мантатов В.В.

Журнал: Вестник Бурятского государственного университета. Философия @vestnik-bsu

Статья в выпуске: 6, 2007 года.

Бесплатный доступ

Для твердых тел одного структурного типа термодинамический параметр Грюнайзена yD линейно зависит от величины у3=(1+и)/(1 - 2ц), являющейся функцией коэффициента Пуассона \у. По характеру зависимости yD от у3 можно провести определенную классификацию твердых тел. Показано, что параметр Грюнайзена yD является однозначной функцией отношения скоростей продольной и поперечной звуковых волн.

Короткий адрес: https://sciup.org/148178166

IDR: 148178166

Текст научной статьи О взаимосвязи между упругими и тепловыми характеристиками твердых тел

О взаимосвязи между упругими и тепловыми характеристиками твердых тел1

Для твердых тел одного структурного типа термодинамический параметр Грюнайзена уи линейно зависит от величины у3=(1+ц)/(1 - 2 ц), являющейся функцией коэффициента Пуассона ц. По характеру зависимости yD от у3 можно провести определенную классификацию твердых тел. Показано, что параметр Грюнайзена уи является однозначной функцией отношения скоростей продольной и поперечной звуковых волн.

On intercoupling between elastic and thermal features of the solids1

For solids of one structure type thermodynamic Gryunizen’s parameter depends linear on value уз~(2 + ц)/(| -- 2ц), which is a function of Poisson. We can possibly conduct certain categorization of solids on the nature of certain dependencies. It is shown that Gryunizen’s parameter yD is an unambiguous function of a relation between dilatation and crosscut velocities of sound waves.

На основе представлений физики твердого тела и теории упругости нами показано, что термодинамический параметр Грюнайзена yD выражается через коэффициент поперечной деформации (коэффициент Пуассона) ц и скорости звука следующим образом

А = —:—*-—- = const, (2) ц² + 2ц²

где vi и vt - скорости продольных и поперечных акустических волн, соответственно. В соответствии с равенствами (I) и (2) по отношению к зависимости yD от величины Уз=(1+цУ(1-2ц) кристаллические твердые тела группируются по типу структуры (табл.),

причем внутри каждой группы функция у0(уз) является линейной, что подтверждает постоянство коэффициента А для твердых тел одного структурного типа. В качестве примера на рис. 1 приводится зависимость уо от уз для веществ, относящихся к III группе (табл.); термодинамический параметр Грюнайзена уп рассчитан по уравнению Грюнайзена [1,2]:

рву

где Р - коэффициент объемного теплового расширения, В - изотермический модуль всестороннего сжатия, V и Cv - молярный объем и молярная теплоемкость при постоянном объеме.

Таблица. Параметр Грюнайзена y_D, коэффициент Пуассона ц, скорости звука v, и V, для ряда веществ (использованы данные из работы [1]. Т=298 К, Ю⁵ Па)

№	Группы	Элементы й соединения	Id		P		Уз		V;, м/с		v„ м/с	A^y_D/y₃		A (2)		Yd (5)
1	I	AgC'l	2,02		0,409		7,74		3145		1207	0,26		0,34		2,79
2		Au	2,8		0,42		8,88		3361		1239	0,32		0,32		2,88
3		AgBr	2,33		0,396		6,71		2845		1159	0,35		0,37		2,57
4	11	Pb	2,92		0,405		7,39		2158		860	0,4		0.36		2,68
5		Pt	2,54		0,39		6,32		3960		1670	0,4		0,39		2,57
6		CsF		1.49		0,318		3,62		-			0,41		-		-

1 Работа выполнена при финансовой поддержке РФФИ (код гранта О5-О1-ООО71а) и гранта БГУ «Лучшая научная школа».

Д.С. Сандитов, М.В. Дармаев, В.В. Мантатов, Д.Н Цыденова. О взаимосвязи между упругими и тепловыми характеристиками твердых тел

7		Ag	2,4	0,379	5,7	3686	1677	0,42	0,44		2,31
8		Та	1,73	0,337	4,1	4147	2039	0,42	0,49	2,00

Продолжение таблицы.

№	Группы	Элемееггы и соединения	Yd	I*	Ys	V\|, м/с	v_t, м/с	A=Yd/Y3	A (2)	Yd (5)
9		Pd	2,4	0,374	5,45	4954	1977	0,44	0,36	2,68
10		Со	2,1	0,357	4,74	5827	3049	0,44	0.53	1,83
11		Си	2,06	0,35	4,5	4726	2298	0,46	0,48	2,00
12	III	RbF	1,41	0,276	2,85	3948	2132	0,49	0,55	1,64
13		KNO,	1,95	0,331	3,94	-	-	0,49	-	-
14		NaC10₃	1,37	0,27	2,76	4240	2380	0,5	0.58	1,83
15		CaF₂	1,63	0,301	3,27	-	-	0,5	-	-
16		Al	2,11	0,34	4,19	6422	3235	0,5	0,5	2,00
17		Rbl	1,73	0,309	3,43	2245	1198	0,5	0,54	1,83
18		NaNOj	1,31	0,257	2,59	4510	2580	0,51	0,59	1,43
19		Mg	1,41	0,27	2,76	5898	3276	0,51	0,57	1,64
20		Y	1,25	0,245	2,44	4106	2383	0,51	0,6	1,43
21		KCJO4	1,64	0,296	3,18	-	-	0,52	-	-
22	IV	Fe	1,68	0,292	3,11	6064	3325	0,54	0,56	1,64
23		NaClO₄	1,56	0,278	2,88	3970	-	0,54
24		Th	1,4	0,254	2,55	2900	1583	0,55	0,56	1.64
25		RbBr	1,5	0,267	2,72	2591	1403	0,55	0,55	1,64
26		RbCl	1,53	0,268	2,73	3077	1658	0,56	0,55	1,64
27		Ni	2,2	0,33	3,91	-	-	0,56	-	-
28		NaBr	1,56	0,27	2,76	3284	1885'	0,57	0,6	1,43
29		KBr	1,68	0,283	2,96	3075	1695	0,57	0,57	1,64
30		W	1,7	0,283	2,96	5233	2860	0,57	0,56	1,64
31	V	NaCl	1,46	0,243	2,42	4666	2755	0,6	0,62	1,43
32		Ni	1,73	0,277	2,86	5894	3219	0,6	0,56	1,64
33		KI	1,63	0,265	2,69	2623	1469	0,61	0,58	1,64
34		A1₂O₃	1,34	0,223	2,21	-	•	0,61	-	•
35		KCi	1,6	0,259	2,6!	4090	2312	0,61	0,58	1,64
36		KF	1,73	0,274	2,82	4641	2587	0,61	0,57	1,64
37		LiCI	1,52	0,245	2,44	5260	3058	0,62	0.61	1,43
38		LiF	1,34	0,214	2,12	7323	4518	0,63	0,65	1,21
39	VI	NFUCIO,,	1,81	0,271	2,78	3800	2130	0,65	0,58	1,64
40		LtBr	1,7	0,256	2,57	3621	2072	0,66	0,59	1,43
4!		Nai	1,9	0,274	2,82	2889	1639	0,67	0,59	1,64
42		NaF	1,57	0,234	2,32	-	-	0,68	-
43	V11	CaF₂	1,55	0,224	2,22	-	-	0,7	-	-
44		CsBr	1,93	0,27	2,76	-	-	0,7	-	■
45		U	1,62	0,23	2,28	3422	2105	0,71	0,63	1,21
46		NaF	1,72	0,24	2,38	5666	3330	0,72	0,6!	1,43

47	CsCJ	1,98	0,264	2,68	-	*	0,74	*	-
48	CsI	2	0,265	2,69	■	-	0,74	-	-
49	Be	0,83	0,034	l,H	13003	8967	0,75	0,73	0,71
50	Lil	2,22	0,265	2,69	2846	1608	0,83	0,58	1,64

Скорости звука V, и vt относятся к линейным (гармоническим) величинам, поэтому коэффициент А не зависит от ангармонизма (нелинейности сил межатомного взаимодействия). В соответствии с равенством (1) это означает, что зависимость параметра Грю-найзена от ангармонизма определяется главным образом множителем уз, который является однозначной функцией коэффициента поперечной деформации ц.

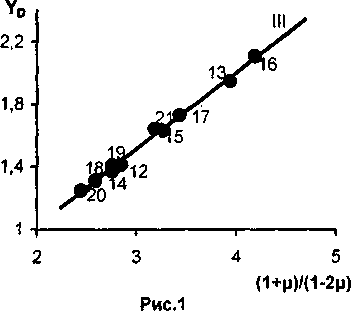
Рис, 1. Линейная корреляция между параметром Грюнайзена y_D и величиной (1+ц)/(1-2ц), где ц - коэффициент Пуассона. Номера точек соответствуют номерам веществ в таблице (группа 111)

Аналогичные графики Yd - уз были построены для оптических стекол. Необходимые экспериментальные данные брали из справочника [2]. Величину уо рассчитывали по уравнению Грюнайзена (3). Термодинамический параметр Грюнайзена y_D для неорганических оптических стекол слабо зависит от природы этих систем. Тем не менее, у стекол с высоким коэффициентом Пуассона, как правило, ангармонизм выражен сильнее, чем у стекол с низким коэффициентом поперечной деформации. Так, например, у сверхтяжелого крона СТК12 имеем ц=0,288 и Yd=0,86, а у легкого крона ЛК7 - ц=0,19) и Уо=0,41. Как и следовало ожидать, для ряда оптических стекол одного структурного типа зависимость уо от величины уз=(1+ц)/(1-2ц) оказывается линейной (рис.2).

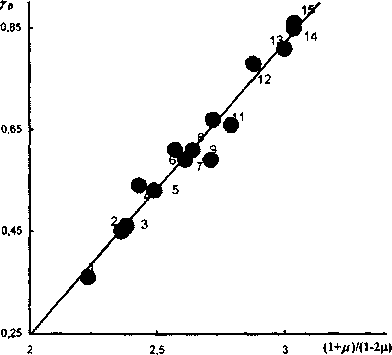
Рис. 2, Линейная корреляция между параметром Грюнайзена yD и величиной (1+ц)/(1-2ц) для оптических стекол. ОФ1 (I), ТФ4 (2), БФ28 (3), ФК14 (4), ТФ7 (5), ФК14 (6), ТК4 (7), ТЮЗ (8), ТК8 (9), ТК16 (10), ТК20 (И), ТК17(12), ТК21 (13), СТК12 (14) и БФ16 (15) [9].

Известно, что коэффициент поперечной деформации ц однозначно определяется ско ростями звука

2-(ц/ц)г

Ц 2-2(и5/и,У ‘

Подстановка ц из (4) в соотношение (1) с учетом (2) приводит к выводу о том, что и параметр Грюнайзена определяется скоростями звука

₌ 3 3(ц/ц)^г-4

Yd" 2^ (v,/^)2 +2 _

Расчет уо по этой формуле находится в удовлетворительном согласии с результатом, следующим из уравнения Грюнайзена (3) (табл.).

Список литературы О взаимосвязи между упругими и тепловыми характеристиками твердых тел

Беломестных В.Н. Акустический параметр Грюнайзена твердых тел//Письма в ЖТФ. -2004. -Т. 30.-Вып. 3.-С. 15-19.
Стекло оптическое бесцветное. Физикохимические характеристики. -СПб.: Изв-во стандартов. -1999. -58 с.

Статья научная