О задаче Стефана и расчетах затвердевания отливок

Для затвердевшей части отливки, т. е. для т >  0 и 0 <  x < ^

д θ       д ²θ

—² = a ₂— 2- д τ       дx ²

.

Здесь a 1 и a 2 – коэффициенты температуропроводности жидкого и твердого метала, м²/с.

Граничные условия:

• а)    для x = 0 и т > 0 9 1 (0, т ) = 9 п ;

• б)    для x = да и т > 0 9 1 ( да , т ) = 9 ж ;

• в)    на фронте затвердевания для x = £ и т >  0 0 i& т ) = 6 2& т ) = 9 кр .

Займемся потоками тепла на фронте затвердевания, где x = ξ. В объеме металла толщиной d^ есть три потока тепла (в Вт/м²): q 1 -поток тепла от жидкого металла к фронту затвердевания; q 2 – поток тепла от фронта затвердевания к поверхности охлаждения; q L – поток тепла, выделяющегося (или поглощающегося) при затвердевании (расплавлении) слоя толщиной d^. Знаки q 1, q ₂ и q L зависят от величины перегрева жидкого металла и интенсивности теплоотвода на поверхности охлаждения. Предположим, что идет затвердевание металла. Тепло передается от более нагретых участков тела к менее нагретым, поэтому потоки тепла q 1 и q 2 противоположны направлениям градиентов температур (и положительному направлению оси x ) и запишутся так:

д θ 1             д θ 2

q 1 = - ^Л 1      q 2 = - Л 2

дx          дx

,,

(3), (4)

где X 1 и Х ₂ - коэффициенты теплопроводности жидкого и твердого металла, Вт/м - град. Раз мы условились, что идет затвердевание, то этот процесс происходит с выделением тепла и q L имеет знак «+»:

dξ qL = + L р2 , dτ

,

где L – удельная теплота кристаллизации, Дж/кг; р ₂ - плотность твердого металла, кг/м³. Температуру объема металла толщиной d ξ можно считать постоянной и равной температуре кристаллизации 0 кр . Поэтому сумма источников и стоков тепла равна 0:

6 1 — 6 ж - ( 6 ж

09 =0 +(0

2       п      кр

-

e кр )

1 - erf ( x /2 T a j ) 1 - erf ( x /2 Ja )

- ⁶ п )

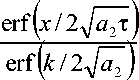
q i + q 2 + Q l = 0-                     (6)

Подставив значения входящих в (6) величин и сделав преобразования, получим:

где erf – функция ошибок Гаусса; k – коэффициент затвердевания, м/с^1/2. Дифференцируя (10) и (11) по x , имеем:

д θ      д θ        d ξ

X, — ² + X. — ¹ = L р . —

² дx ¹ дx      ² d τ

.

д 6 1 _ ^(e ж - ⁶ ) exp ^{(- x2}1 ^{4 a} i ) dx      [ 1 - erf ( x / 2 .Ja )]V ^ai пт

Общепринятой является запись в таком виде (так называемое условие Стефана):

дθ2     дθ1

X<            X/]

дx      дx        dτ .(

Хотя непонятно, как получено это выражение. Если из потока тепла q 2 вычесть q 1 и приравнять q L , то получится

• дθ     дθ

• - X, — ² + X. — ¹ — L р , —

дx      дx       dτ ,( а не соотношение (8). По-видимому, значения q1 и q2 были взяты со знаком «+», из q1 вычли q2 и приравняли qL. Все дело в этом знаке «+» перед вторым членом выражения (7), а не «–», как у И. Стефана, Ф. Ноймана и других. Дальнейший ход решения известен. Наиболее подробно, без пропусков простых преобразований он изложен в книге [2]. Достаточно хорошо рассмотрена тема в книгах [11-13]. Правда, во всех этих четырех книгах используется зависимость (8), а не (7). Посмотрим, к чему приведет неверная запись тепловых потоков на фронте затвердевания. После ряда преобразований имеем такие соотношения для текущих температур жидкой и твердой фаз:

д 6 2 ₌ ( ⁶ кр ^{- 6} п ^{) ex}P ^{(- x} 7 ^{4 a} 2 ) dx     erf ( x / 27 0"а пт

Толщина затвердевшей корочки изменяется во времени так:

^ — x 4т а производная dξ   k dτ  2 τ

Коэффициент аккумуляции тепла жидкого металла

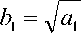
твердого металла b2

— 2 /

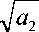
Подставляя (12), (13), (15) в (7) и учитывая (16) и (17), окончательно имеем:

b2 (6 кр - 6 п )         _          b1(6 ж - 6 кр )________ УЛ exp (x2/ 4a2 )erf (kj 2^2)  exp (x2/ 4a, )[1 - erf (x/ 277)]   2    2

В статьях и книгах [2-13] итоговая зависимость отличается от (18) знаком «+» перед вторым членом этого выражения. Назовем формулу этих книг и статей как (18St). Знак «+» меняется на «–» в (7), а «–» на «+» в (8) из-за того, что правая часть выражения (12) имеет знак «–» и после подстановки в (7) или (8) происходит смена знака перед вторым членом уравнений (18) и (18St). Выясним, к чему приведет замена знака с

«–» на «+» в формуле (18St) по сравнению с (18). Для этого проведем расчеты затвердевания по выражениям (18) и (18St). На примере чугунной отливки – неограниченной плиты толщиной 2 X = 30 - 10^-3 м. Значения коэффициентов возьмем из книги [14]: Х 1 =18,6 Вт/м - град; Х 2 =36,2 Вт/м - град; c 1 838 Дж/кг - град; c 2 =753 Дж/кг - град; р 1 =6950 кг/м³; р ₂=7200 кг/м³; L =215 000 Дж/кг; 0 ж =1280 ° С; 0 кр =1180 ° С; a i =31,9 - 10^-7 м²/с;

a 2 =66,7-10^ м²/с; b 1 =10400, b 2 =14000, Ь ф =1380 Вт - с^1/2/м² - град. Нужно задаться температурой поверхности металла. Для граничных условий 1го рода рассчитаем ее по следующему соотношению [11]:

θ

п

= 6

кр

^Ь 2   ^Ь ф

1 + b 2 / Ь ф

Получаем 0 п =1074 ° C, или Т п =1094 ° С. Хотя формы, конечно, нет. Просто поддерживается на поверхности отливки такая температура,

соответствующая затвердеванию отливки в песчаной форме, но при отсутствии формы. 0 п нельзя принимать равной 0 кр : будет мал отвод тепла от отливки. Результаты расчетов приведены в таблице. Величину коэффициента затвердевания изменяли от 0,500 - 10^-3 до 5,000 - 10^-3 м/с¹ / ². Обозначения в табл. 1 такие: A , B и C – это первый, второй и третий члены выражений (18) и (18St), A + В – суммирование по (18St), A – B – вычитание по (18). A , B , A + B , A – B и C измеряются в Вт - с^1/2/м² и должны быть умножены на 10 6 .

Таблица 1. Влияние коэффициента затвердевания на отвод тепла от отливки

k •IO3, м/с1 / 2	A	B	A + B	A - B	C
0,500	12,754	1,211	13,965	11,543	0,662
0,800	7,893	1,317	9,210	6,576	1,059
1,000	6,250	1,390	7,640	4,860	1,324
1,301 *	4,727	3,006	7,733	1,721	1,722
1,500	4,043	1,579	5,622	2,464	1,986
1,605	3,747	1,619	5,366	2,128	2,125
2,000	2,900	1,775	4,675	1,125	2,647
2,084 **	2,759				2,759
2,500	2,190	1,939	4,129	0,251	3,310
2,950	1,742	2,167	3,909	–0,425	3,906
3,000	1,694	2,182	3,876	–0,488	3,972
4,000	1,059	2,619	3,678	–1,560	5,300
5,000	0,663	3,071	3,734	–2,408	6,620
5,260 *	0,584	6,378	6,962	–5,793	6,964

Примечание: * - перегрев чугуна θ _ж – θ _кр = 200ºC; ** - перегрев чугуна θ _ж – θ _{к р} = 0ºС

Начнем с решения уравнений (18) и (18St). В книгах [2, 3, 11-13] утверждается, что выражение (18St) очень сложно и его нужно решать графически. На самом деле (18) и (18St) решаются элементарно, нужно задаться несколько раз (5-7 раз) значением k , вычислить значения A + B и A – B и добиться, чтобы отличие этой суммы или разности от C не превышало заданной величины.

Теперь об обещанном доказательстве ошибочности выражения (18St). При нулевом перегреве, то есть при равенстве 0 вторых членов уравнений (18) и (18St) коэффициент затвердевания равен 2,084 - 10^-3 м/с¹ / ² по обеим формулам (см. табл. 1). При перегреве 100 и 200 ° C этот коэффициент получается равным 1,605 - 10^-3 и 1,301 - 10^-3 по зависимости (18), 2,950 - 10^-3 и 5,260 - 10^-3 м/с¹ / ² - по (18St). То есть с увеличением перегрева коэффициент затвердевания (и скорость затвердевания) по соотношению (18St) растет (?!), а не уменьшается, как это должно быть и как получается по (18).

Как видно, уравнения (18) и (18St) имеют решения . Замена «+» на «–», т. е. переход от (18St) к (18) ведет к важному результату:

значительно уменьшается расхождение между теоретическими и экспериментальными значениями коэффициента затвердевания. В данном примере теоретическое значение k при переходе от (18St) к (18) уменьшилось с 2,950-10-3 до 1,605-10-3 при экспериментальном его значении * 0,8-10-3 м/с1/2 [15]. Разница между теоретическим и экспериментальным значениями k стала равной 2, а не 3,7. Хотя время затвердевания будет больше теоретического в соответствии с (14) в 22 = 4 раза по (18) и в 3,72=13,7 раза по (18St). Разница в 4 раза (для данного конкретного случая затвердевания чугуна в песчаной форме при ГУ1), конечно, существенная, но все же это не 13,7 раза, как получается при расчете по (18St). Хотя и была принята температура поверхности отливки, какой она была бы при затвердевании чугунной отливки в песчаной форме при идеальном контакте, и, следовательно, завышенном теплоотводе по сравнению с реальными условиями литья. При ГУ1 термическое сопротивление отводу тепла от стенки отливки равно нулю, а поверхность отливки мгновенно принимает температуру окружающей среды, то есть 0п. Лимитирующим звеном в процессе охлаждения является внутренний теплообмен – отвод тепла твердым металлом. Это внутренняя задача. На практике ГУ1 осуществляют при очень высокой интенсивности внешнего теплообмена, например, при закалке изделий в жидкостях, температура кипения которых ниже температуры нагрева изделий под закалку. При этом температура поверхности остается постоянной и равной температуре кипения жидкости [16]. Например, при закалке данной чугунной отливки при 0п = 80°С рассчитанный по (18) коэффициент затвердевания составляет 4,572-10-3 м/с1/2. При ГУ1 нет проблем с отводом тепла с поверхности отливки: все тепло «убирается» каким-то образом. Но при литье теплоотвод с поверхности отливки ограничивается не подводом тепла из центра отливки к ее поверхности, а от поверхности отливки внутрь формы. Это задача внешняя, теплоотвод определяется отводом тепла формой, а у песчаной формы коэффициент аккумуляции тепла на порядок ниже коэффициента аккумуляции тепла отливки. Теплоотвод от отливки гораздо ниже, чем при ГУ1, когда мы задались 0п из расчета температуры идеального контакта отливки и песчаной формы. Расхождения между теоретическими и экспериментальными значениями k объясняются не тем, что 0п меняется во времени (этим можно пренебречь за время затвердевания отливки), или изменением свойств металла и формы. bф определяется при заливке в заданную форму по времени затвердевания при минимальном перегреве. Изменение свойств металла невелико, по крайней мере, никак не объясняет 4-кратное замедление времени затвердевания по сравнению с теоретическим. Дело в изменении задачи с внутренней на внешнюю из-за резкого замедления отвода тепла с поверхности отливки.

Как же выйти из этого положения? Нам нужно сохранить 0 п = 0 по = 0 пф , где 0 по и 0 пф -температура поверхности отливки и температура поверхности формы. Иначе невозможно получить решение в замкнутом виде, т. е. в виде интегралов от элементарных и специальных функций. И в то же время задать равенство тепловых потоков из отливки и в форму:

д θ ₂        д θ ф

— ^7 --- = -Кд --- дx       дx

.

То есть используются одновременно ГУ1 и ГУ4. Конечно, в случае идеального контакта отливки и формы равенство (20) выполняется. И в работах С. Шварца [17, 18] было получено выражение, учитывающее литейную форму, отличающееся от (18St) только первым членом и появлением знака «–» между первым и вторым членами.

Обозначим формулу С. Шварца как (18S) и приведем только часть ее:

b2θкр exp (k2/ 4a2 )[b2/ Ьф + erfk 2 ja)]    (18S)

Сначала займемся знаком «–». На самом деле должен быть «+» из-за того, что после подстановки (12) в (8) два «минуса» дадут «плюс». Расчет по (18S) при прежних условиях дает £=0,342-10-3 м/с1/2, что в 2,34 раза ниже экспериментального значения k, а время затвердевания, следовательно, будет в 2,342 = 5,48 раза больше опытного. Таким образом, формула (18) дает значения k, в 2 раза большие, (18S) – в 2,34 раза меньшие экспериментальных. А по (18St), как уже говорилось, расчетные значения k в 3,7 раза больше опытных. Однако положение еще хуже, чем оно может показаться из сказанного. Дело в том, что при наличии формы резко замедляется отвод тепла от твердой корочки металла, а формулы (7) и (20) не отражают этого, а (18S) учитывает это не полностью. По (7) и (20) для твер-дθ дой корочки поток тела q2 = -к2 —2, но ведь дx форма отводит тепла гораздо меньше. Известно, что величина потока тепла в форму при постоянной температуре на ее поверхности определяется так [11, 19]:

Ч ф =

—

b ф θ

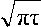
Мы можем убрать форму, но считать, что тепло от твердой корочки уходит в форму в виде потока q ф . Понятно, что выражение (20) верно, но в (7) стоит q 2 – сколько может отвести тепла твердая корочка. А ведь форма «возьмет» тепла значительно меньше. Нужно ориентироваться на q ф . Теплоотвод лимитируется формой, а не твердой корочкой металла. Поэтому (6) следует записать в таком виде:

qi + Яф + Ql = 0

, а (7) будет выглядеть так:

д θ2   b ф θ п        d ξ

К^ 1 L р₉

дx πτ      dτ

Однако уравнение (23) может быть решено только численными методами и должно стать предметом отдельного исследования. А пока сказать что-нибудь об этом решении невозможно.

Из зависимости (18) можно сделать следующее важное заключение. Приравняем второй член этого уравнения нулю, а теплоту перегрева

добавим к теплоте кристаллизации в правой части:

.   b2(еV9,п)   „=р2k[L+c (е. -екр)]

exp (к ²/ 4 a ) erf ( к / 2 .^а )    2

При перегреве в 100 ° С к будет равен 1,605 - 10^-3 и 1,790 - 10^-3 м/с¹ / ² соответственно по (18) и (24), а перегрев в 200 ° С дает 1,301 - 10^-3 и 1,602 - 10^-3 м/с^1/2. То есть включение теплоты перегрева в теплоту кристаллизации приводит к увеличению коэффициента затвердевания на 11,5 и 23,1% по сравнению с его учетом во втором члене уравнения (18). А время затвердевания отливки будет соответственно в 1,24 и 1,52 раза меньше – весьма значительные величины. Надо сказать, что, что уравнение Стефана получено для полубес-конечного тела. И использование этой зависимости для тел конечных размеров дает завышенную величину времени затвердевания отливки.

Рассмотрев работы И. Стефана и С. Шварца по затвердеванию, сделаем обзор существующему положению дел. Все последующие работы сводятся к двум формулам для определения времени затвердевания отливки. Первая из них записывается так:

т затв

^{П ХX} [ c l Р 1 ^{( е} ж ^{- е} кр ^{)+ L} р 2 | 2Ь ф ^е п

По второй подсчитывается текущая температура отливки [20], задаваясь которой находят время достижения отливкой этой температуры:

е = е [ 1 - erf ( toVT ) ] exp ( го²т )

, где начальная температура отливки

е н = е кр +

с (еж - е„)+l

1 ж     кр

c ₂

,

а коэффициент

го =

b ф

с ρ X

В (27) теплота кристаллизации суммируется с теплотой перегрева, переводится в температуру и прибавляется к температуре кристаллизации. Как уже говорилось, судя по (18) и (24), простое сложение теплоты перегрева и теплоты кристаллизации приводит к завышению коэффициента затвердевания, что, конечно, скажется

и на (25). По-видимому, это относится и к (26). Включение теплоты перегрева в теплоту кристаллизации первым произвел С. Сайто в 1921 г. [21]. Затем формула (25) с незначительными отличиями приводится в статье Н. Хворинова [22] и используется во многих статьях и книгах, в т. ч. во всех книгах А.И. Вейника и Г.Ф. Баландина. Не занимаясь обсуждением этих отличий, отметим только, что в знаменателе (25) должна быть 0 _п , а не 0 _кр . Анализ зависимостей (25) и (26) проведен в статье [23].

Расчет времени затвердевания отливки по (25) и (26) дает близкие результаты. Так, т затв по (25) для чугунной отливки с 2X = 30 - 10^-3 м равно 317 с, по (26) – 296 с. И какая из этих формул точнее, может рассудить только эксперимент. Но зависимость (26), в отличие от (25), не требует постоянства коэффициента затвердевания и пропорциональности толщины намерзшей корочки корню квадратному из времени (не используется «закон квадратного корня»), не нужно принимать 0 _п = const. Температура контакта отливки с формой непрерывно меняется. И, что очень важно, выражение (26), в отличие от (25), может быть использовано для расчетов охлаждения отливки в форме до заданной температуры – температуры выбивки. Причем в литературе нет формул, по которым можно было бы рассчитать охлаждение отливки до нужной температуры, так как имеющиеся зависимости неудовлетворительны по своему математическому обоснованию. По (26) время охлаждения чугунной отливки с 2 X = 30 - 10^-3 м до 500 ° С составляет 9660 с, по экспериментальным данным оно равно 9000 с.

Учитывая, что формула (25) за 91 год не претерпела существенных изменений, на первый план выходит зависимость (26), которая к тому же дает расчет времени охлаждения отливки до заданной температуры. Выражение (26) получается путем строгого решения дифференциального уравнения теплопроводности Фурье для формы. По-видимому, дальнейшие усилия исследователей должны быть направлены на определение граничных условий на фронте затвердевания и на поверхности контакта отливки с формой, анализе и усовершенствовании формулы (18) и получению решений по типу (26).