О законах сохранения энергии в ньютоновской механике

Как следует из названия статьи, настоящая работа посвящена констатации факта существования множества различных соотношений, подобных ‘закону сохранения энергии’ (ЗСЭ), при одних и тех же движениях системы тел/материальных точек (м/т). Значимость приведенного заключения подчеркивается тем, что до настоящего момента известен и хорошо исследован единственный ЗСЭ. Ценность этого ЗСЭ (как и любого другого соотношения в виде уравнения сохранения) состоит в том, что он «позволяет рассмотреть общие свойства движения без решения уравнений и детальной информации о развитии процессов во времени» [1, c. 128]. В этой связи рассмотрение других ЗСЭ существенно расширит возможности подобных исследований.

На возможность формирования других энергетических описаний в принципе указывалось в [2, c. 166], полагая, что надо “найти такое выражение для функции энергии, которое бы не зависело от времени и которое бы находилось в согласии с уравнением F = та”. Однако авторы в итоге рассматривали общеизвестный ЗСЭ.

В работе сформулированная выше задача решается в два этапа. На первом этапе с общих позиций для одной и той же системы взаимодействующих тел доказывается возможность существования множества различных соотношений, подобных ЗСЭ. На втором этапе при рассмотрении движений в замкнутой системе конечного числа взаимодействующих тел находятся два различных соотношения из множества возможных ЗСЭ. Важным аспектом рассмотрения различных ЗСЭ является их сопоставимость. Под сопоставимостью в данном случае понимается одинаковость структуры ЗСЭ и одинаковость размерностей.

Но прежде, чем двигаться далее, необходимо ответить (хотя бы для себя) на вопрос, что такое ‘энергия’? К сожалению, несмотря на долгую предысторию, в физике нет единого ответа на этот вопрос. Так в работе [3, c. 156] полагают, что ‘энергия’ “никогда не создается и не уничтожается, она может только переходить из одной формы в другую”. Такой же точки зрения придерживаются и в ([4, с. 210-211], [5, с. 115]). В противовес этой точки зрения, другой и очень уважаемый автор [6, с. 72, 74] отмечает, что ”физике сегодняшнего дня неизвестно, что такое энергия”, и что “закон сохранения энергии – это, по существу, математический принцип, утверждающий, что существует определенная величина, которая не меняется ни при каких превращениях, существующих в природе”. И наконец, в работе [5, с. 124] уже конкретно утверждается, что “уравнение фазовой траектории представляет собой уравнение закона сохранения энергии”. Однако при рассмотрении последнего утверждения имеются особенности, которые нужно учитывать. Суть состоит в том, в каком виде (в явном или неявном) рассматривается уравнение фазовой траектории. К сожалению, представить фазовую траекторию в явном виде – это математически непростая задача. Гораздо проще фазовая траектория представляется в неявном виде. Более того, для единственной фазовой траектории, представляемой в явном виде, можно указать множество неявных форм, частным случаем которых могут быть соотношения, подобные ‘закону сохранения энергии’. Это и определяет возможность существования множества различных соотношений, подобных общеизвестному ЗСЭ.

Начнем с простых пояснений. Напомним, что ‘фазовая траектория’ - это геометрическое место точек в ‘фазовом пространстве’, представляющем скоростные и координатные параметры движения системы в каждый момент времени. В простейшем одномерном случае взаимодействия двух тел размерность фазового пространства [v₁, V ₂ ,x ₁ ,x ₂ ] равна 4. Для каждого тела фазовые траектории v₁ = /₁(x₁,x₂) и V ₂ = / 2 (x₁, x₂) в явном виде отображаются в трех мерных пространствах с координатами (v₁,x₁,x₂) и (v₂,x₁, x₂), где x _i есть координата, а v _i скорость i -ого тела в один и тот же момент времени. Введем некие взаимно однозначные преобразования ф i (arg') и применим их к обеим частям соотношений V i =/ i (x₁,x₂) соответственно. Получим новые соотношения V i (V i ) = V i (/ i (x₁, x₂)). Теперь вычтем и прибавим к координатным составляющим произвольные постоянные величины C i . Получим для каждого i зависимости V i (v i ) = ^[ ^ i⁽ / i^(x1^,x2^{)) — C}i ] + ^Ci или V i^i ) + [C_i — V_i(/_i( ^x ₁, x₂))] = C. Обозначим скоростную (‘кинетическую’) составляющую T i = V i (V i ), а координатную составляющую U i = [Ci — ViCfife^))]. Следствием этого являются две неявные формы представления фазовых траектории V i = /_i(x₁, x₂) как суммы ‘скоростной’ и ‘координатной’ составляющих вида T + U i = C i для каждого i. Самый простой способ объединить эти параметрические соотношения в единую зависимость есть их сложение: T = T₁ + T₂, U = U₁ + U₂, C = C₁ + C₂. В итоге в 4-х мерном пространстве [v₁, v₂,x₁,x₂] возникает в виде традиционного ‘закона сохранения’ соотношение

T + U = C, где T = T(v₁, v₂) , U = U(x₁, x₂). Легко видеть, что вводя различные преобразования V i (arg) и постоянные C i , можно получить бесчисленное количество ‘законов сохранения’ вида T + U = C. Изложенное относительно просто распространяется на случай рассмотрения неявных форм представления единственной фазовой траектории, описывающей движения и взаимодействующих тел в 6и мерном пространстве [скорости-координаты] (r₁, V 2 , .„, v_n) = 0(Г 1 ,Г 2 , ...^J.

Таким образом, при рассмотрении неявных форм представления единственной фазовой траектории возможно появление множества различных соотношений, подобных ‘закону сохранения энергии’.

Теперь можно перейти ко второй части. В рамках моделей классической механики движения и взаимодействующих тел представляется и траекториями r i (t) в четырехмерном пространстве [координа-ты-время]. Другой способ представления этих же движений возникает при переходе в ‘фазовое’ пространство, в котором вместо и траекторий в пространстве [коорди-наты-время] рассматривается единственная фазовая траектория в 6и мерном пространстве [скорости-координаты] О1 , V 2 , ..., г_п) = 0 ⁽ Г 1 , Г 2 , ..., rj.

Так как целью настоящей работы является установление факта существования для одной и той же механической системы нескольких различных соотношений, подобных ‘закону сохранения энергии’, то некритичными будут некоторые допущения, которые упростят записи.

Первое допущение будет состоять в использовании моделей только классической и Ньютоновской механик, включая абстракцию (или модель) материальной точки (м/т), для описания замкнутой механической системы с произвольным количеством взаимодействующих элементов.

Второе допущение будет состоять в рассмотрении ‘одномерной’ задачи. Это означает, что уравнения движений всех м/т системы должны быть записаны в двумерном пространстве ‘координата - время’ [x, t]. При этом все м/т будут располагать- ся на некоторой оси X , все силы, скорости и ускорения будут направлены вдоль этой же оси. Определяя на оси X начало координат, получаем возможность указать координату 'х' для каждой м/т. Пронумеруем все м/т так, чтобы Xt+1 > Xt, i = 1,2, ,„,(п — 1) . Рассматривая движения всех м/т в соответствии со вторым законом Ньютона, можно описать движения всех точек системы в виде системы п дифференциальных уравнений (ДУ) mtXt(t) = Ft, где i = 1, ...,п и где Ft есть сила, действующая на i -тую м/т. С другой стороны, каждая м/т взаимодействует с остальными (п — 1) м/т системы, что позволяет записать Ft = Z£=1,k*t Ftk = Zk-i, Ftk + £k=t+1 Ftk, где Ftk есть сила, действующая на i -тую м/т со стороны k-той м/т. Всего таких сил будет четное число [п(п — 1)]. В соответствии с третьим законом Ньютона в замкнутой системе п взаимодействующих м/т каждой силе Ftj будет соответствовать сила Fjt = —Ftj. Назовем ‘силами действия’ такие Ftj, для которых j > i. Всего ‘сил действия’ будет [n(™ И] Соответственно силы Fjt будут называться ‘силами противодействия’. Выражая все ‘силы противодействия’ через ‘силы действия’, получим Ft = — Zk-i,Fkt + Zk=t+1,Ftk.

Если бы все силы ‘действия’ Ftj были бы известны, то несложно найти все решения системы ДУ. Однако в большинстве случаев эти силы неизвестны. В этой связи введем третье допущение (ограничение), предположив, что каждая сила Ftj будет являться непрерывной и ограниченной функцией ftj расстояния 8tj между взаи модействующими точками, т.е. Ftj = ftj(^tj). Очевидно, что число таких ‘расстояний’ будет равно количеству сил ‘действия’, т.е. [n(™ 1)]. В нашем случае расстояние Stj определяться, как 8tj = (xj — Xt) > 0, где j > i и, естественно, Xj > xt. В этом смысле 8tj = d1(x, у) = |х — у|, где х = Xt, у = Xj и где d, есть метрика [7, с. 27]. Т.е. расстояние 8tj удовлетворяет всем требованиям, предъявляемым к метрическому отображению неупорядоченных пар элементов множества [х] на действительную полуось R+. Упоминание о метрических свойствах расстояния Stj целесообразно в связи с тем, что в дальнейшем будут рассматриваться дифференциальные уравнения в отношении §tj, которые будут называться ‘метрическими уравнениями’. Укажем еще на одно свойство ‘расстояний’, которое будет называться ‘кинематическим’ свойством. Указанное свойство состоит в возможности операций сложения ‘расстояний’, а именно: для г > j > i имеет место 8tj + 5jr = Str.

Имея в виду третье допущение, можем записать, что

^ t^Xt = ^— Z k=¹1,^fkt^(Skt⁾ + Z k=t+1,^ftk^(Stk )   ⁱ = ^1, - ^{,п ,               (1)}

где S kt = (X t — X k ) для k <  i и 8 tk = (x _k — X_t) для k> i. Дифференциальные уравнения системы (1) записаны в пространстве ‘координата - время’ и, если не рассматривать особых случаев, относятся к обыкновенным ДУ, решения которых существуют и единственны.

Другой способ описания движений в системе n взаимодействующих м/т состоит в рассмотрении ‘расстояний’ 8 _tj = (x j — X t ), для всех i и j > i. Отметим, что

8-- = °tj

/ dX j

⁽ dt

(xj

d§ ij dt

—

= ^j

dxA   (

) = (Vi dt J ^j J

^{— X}d =

dX j — dx _t .

^(xj ^—Xt) =

— v _t ). Кроме того, S _tj =

^dv 8 _t j     d(y j -V i )

dt        dt

и     d8 _tj =

Возвращаясь к исходной системе ДУ, 11

запишем Xt =—F и Xj =—F . Теперь

m [          ^J    m j

3 ^tj = ^(x j — ^Xt) = m - ^Fj^—mr_t^Ft или

(m t mj)8 tj = [(.+m_i ⁾ F j + (—m j )F t ]

(2),

где P i = - Z k-=i, ^fki (М + Z fc = i + 1,^fik⁽⁽ ^ ik⁾ и F j = -^k^f kj ^S kj ) + Z fc=j + i,^fjk⁽ ^ jk⁾ . i = l, ^,n-l, ^j >  ⁱ , j = 2, .„,n. Будем называть уравнения системы (2) ‘метрическими дифференциальными уравнениями’.

Теперь можно перейти от пространства ‘координата - время’ [x,t], в котором представлены уравнения систем (1), (2), к фазовому пространству ‘скорости – координаты’ [v1, .,vn,x1, .,xn]. Один из стандартных способов такого перехода [8, c. 267 – 269], [9, c. 40], [1, c. 132] состоит во введении в исходные ДУ второго порядка ‘скоростных’ переменных и исключении времени. Это приводит (если не вводить дополнительные преобразования) к формированию системы ДУ первого порядка в пространстве ‘скорости – координаты’, которые должны быть проинтегрированы.

Начнем с рассмотрения уравнений системы (1), введя скорости V i = ^ , избавляясь от времени и интегрируя. В итоге получим

J m^d^ = - Z k=i, J f ki (^ i — ^ k )dX i + Z £=i+i, J f i_k (x _k — x i ) dx i      (3),

где i = 1,..., n.

Проблема состоит в том, что каждый интеграл в правой части i -того уравнения представляет собой интеграл от функции двух зависимых переменных по одной из этих переменных. При этом среди интегралов от силы ‘действия’ F ik = f ik ^X k — X i ) в i -том уравнении системы (3) при к = j > i найдется J f _ij (x / — x _i )dx _i . В то же время в j-том уравнении системы (3) Jm j V j^d V j = - Z k-^iJ ^fkj^(xj - ^xk ) ^dxj + Z k=j+i, J ^fjk^(xk - ^xj) ^dxj среди интегралов от силы ‘действия’ F kj = f _kj (x j — x _k ) при к = i < j найдется ^— J ^fij^(xj - ^xi ) ^dxj = J ^fij^(xj - ^xi ) ^(—dxj) .

Если все уравнения системы (3) сложить, то получим (при суммировании в правых частях по всем ‘силам действия’): T, i>=1 J^miVi^dVi = ^— Z r=^-i¹ Z y = i+i J ^fij ( ^xj ^— x i ) (dx j — dx i ). Или учитывая упомянутые ранее 5^ = (x j — x _i ) и d5 _ij = (dx j — dx _i ), будем      иметь      ^ ” ₌₁ J m _i v _i dv _i =

• — Z^ -i¹ Z y=i+i J f ij (S ij) dS ij (4), где в правой части представлены только ‘силы действия’. Так как, согласно третьему допущению, функция f ij (S ij' ) является непрерывной и ограниченной функцией расстояния 5 ij , то интегралы в левой и в правой

частях (4) находятся обычным способом:

и 2 ^i m_tV i dV i = m i- ^-+C_v.

^{и   J f}ij⁽⁵ij) ^d5ij = ^ ij^(Sij) ^{+ C}(6 _tj ) = ^фij^(xj ^{— x}i) ^{+ C}(6 _tj ) ,

позволяет записать

ZP=i mi"^ + Xi-1 Zjj=i+i ^ij(xj — xi) = Ci что

Это – неявная форма представления фазовой      траектории      (v₁, v₂, ..., v_n) =

0(x i ,x 2 , ..,x _n ).

Обратим внимание, что общий вид неявной формы (5) это – уравнение сохранения, что имеется группа ‘скоростных’ параметров, традиционно обозначаемая как ^vi

• 1 ₁ = Z i=₁ m i- .- , что имеется группа координатных’ параметров, тоже традиционно обозначаемая      как              U =

ZF=-11Z7=i=1Фij(xj — xi), и, наконец, сум- му постоянных интегрирования можно обозначить как Е1 = C1. Все это позволяет ввести соотношение, подобное ’закону сохранения энергии’ Т1 + U = Е1. Необходимо подчеркнуть, что неявная форма (5) полностью соответствует общеизвестному ‘закону сохранения энергии’. Кроме этого отметим, что также как и для общеизвестного ‘закона сохранения энергии’ имеет место р.. F ij

ди дбм

Более того, имея в виду представление Ft = - Zk=i, Fki + Z^i+1, Fik, можно запи-..     ди    „     ди        - сать, что F.      -.  ’      „.. и   Ft =

_уi-1 ^ди I уп      ^ди

^ ^к=1,д6_к1 + ^Lk=ⁱ⁺¹,d6_{i k} ^.

Теперь вернемся к уже рассмотренным ранее описаниям системы в виде системы дифференциальных уравнений (2). Вводя скоростные координаты и избавляясь от времени, получим аналог дифференциального уравнения (2) в фазовом пространстве dv»4 mimJV^^ =

Спецификой дифференциального уравнения (7) является то, что для указанных диапазонов i и j это уравнение прямо не интегрируется из-за того, что в Fi и в Fj входят силы, действующие на расстояниях ^kj, ^jk, ^ki, ^ik, отличных от расстояния dij, на котором должно происходит интегрирование. Проблема становится разрешимой, если просуммировать уравнения (7) для всех i и j > i. Общее количество слагаемых в левой части такой сумме есть  [“(П—1)]. Подобное суммиро- вание можно проводить разными способами, одним из которых использован в (5). Используя такой порядок суммирования, получим Zn=-i1Zjl=i+imimjV5ijdv5ij = Zn=-i1Zjl=i+i[(+mi)Fj + (-mj)Fi]ddij. Если обозначить Wj = [(+mi)Fj + (-mj)Fi]d5ij, то итоговое соотношение примет вид

Z^ i^{1 Z}?=i+i ^mi^mj v_5i j ^d v₅. j = Z^ i¹ Z “=i+i Я^-                 (8).

Раскрывая выражения в правой части по всем ‘расстояниям’ 8kj, djk, dkl, 5ik, найдем, что составляющая Wij в (7) равна (-MFijd5ij>), где М есть масса всех мате- риальных точек системы. В этом случае выражение (7) оказывается вполне интегрируемым zn=1Z“=i+imimjVSijdvSij = -Zn=i1Zjt=i+iMFijddij или zn=1Z“=i+iJ^i^jvSjdvSij = - zn=11 z“=i+i J Fijddij                        (9), что дает ZKt Z“„+i 2£2>(2i-^ + c.,,. = - Z?-! Z“=i+i (^ij (6ij) + C(S1.)) и

Z ⁿ ; z j i + _i___⁽_ + z ⁿ i z j i + ^Vi, ,. -_{X i} ) = c ₂                (10).

Обратим внимание, что соотношение (10) это другая неявная форма представления фазовой траектории (v1,v2, - ,vn) = 0(x1, x2, „. ,x?). При этом, общий вид неявной формы (10) – это уравнение сохра- нения, что параметров чаемая как

имеется группа ‘скоростных’ в традиционном виде обозна- _т     n-1yn     ^m i ^m j (v j —.i)²

*2 Zi=i Zj=i+i м     2   , что имеется группа ‘координатных’ параметров, тоже в традиционном виде обозначаемая как U = Z”=1Z’n=l+\ ^ij(xj — Xi) и, наконец, сумму постоянных интегрирования можно обозначить как Е2 = C2. Все это дает соотношение, подобное известному ’закону сохранения энергии’ Т2 + U = Е2. Это соотношение отличается от полученного ранее при использовании уравнений (1), но в силу одинаковых структуре и размерностям сопоставимо с Т1 + U = Е1. Если пользоваться установившейся терминологией, то ‘потенциальная’ энергия для уравнений (5) и (10) в данном случае оказывается одинаковой, в то время как ‘кинетические’ энергии Т1 и Т2 при одинаковой размерности различа- ются, как по свойствам, так и по номинальным значениям. Результаты численного моделирования для п = 2 подтвердили справедливость теоретических заключений.

Соответствующие графики имеют вид:

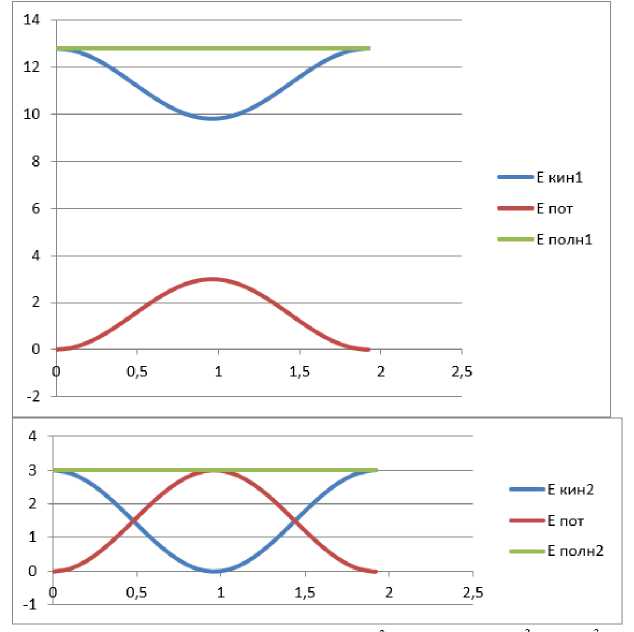
m , m 2   ⁽ V 2 -V 1 ^{) 2}                   V 2        V 2               fe-X i—O

^На этих графиках: ^Е _КИ н 1 = _(mi+m2) ------ , ^Екин 2 = ^ 1 — + ^ 1 — , ^Епот = к-------

^Еполн1   ^Екин 1 ^{+ Е}пот ,   ^Еполн2   ^Екин 2 ^{+ Е}пот ^.

Отметим, что можно указать на неэквивалентные алгебраические преобразования, согласно которым из формы Т₂ = гп-1 vn ^m i ^m j (^v v ^-v i ) 2 1

Z i=1 Z ₇-=i+1 _{м 2}— получается форма

V2

Т1 = 2?=1 ^z тр и наоборот. Эти алгебраические преобразования имеют специфику, состоящую в том, что необходимо вводить в эти преобразования ‘закон сохранения импульса’, причем в квадратичной форме (2Г=1^1^()2. Собственно наличием постоянной величины (2Г=1^1^1) в той или иной формах и объясняется различия в значениях Т1 и Т2.

Заключение : С общих позиций можно утверждать, что соотношения, подобные ‘закону сохранения энергии’ (ЗСЭ), представляют собой неявные формы представления единственной для конкретной механической системы ‘фазовой траектории’. При этом неявных форм много, а фазовая траектория – одна. В работе для одной и той же механической системы найдено два различных соотношения, подобные ЗСЭ. Тем самым подтвержден факт, что, кроме общеизвестного ЗСЭ, имеют место и другие соотношения, отличающиеся от общеизвестного своими свойствами и номинальными значениями.