О законе распределения логарифмического декремента при моделировании микроускорений
Автор: Белоусов Анатолий Иванович, Седельников Андрей Валерьевич
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Авиационно-космическое машиностроение
Статья в выпуске: 1-2 т.14, 2012 года.
Бесплатный доступ
В работе рассмотрена модель микроускорений внутренней среды космической лаборатории, орбита которой содержит освещенный и теневой участки, со случайным логарифмическим декрементом. Случайность вызвана тем, что заранее неизвестно на каком участке орбиты включится двигатель системы ориентации. При больших перепадах температур больших упругих элементов лаборатории логарифмический декремент нельзя считать постоянным. Рассмотрен самый неблагоприятный сценарий включения двигателя. Оценены создаваемые микроускорения для космической лаборатории типа «НИКА-Т».
Микроускорения, логарифмический декремент, закон распределения
Короткий адрес: https://sciup.org/148200622
IDR: 148200622 | УДК: 629.783+523.3
Текст научной статьи О законе распределения логарифмического декремента при моделировании микроускорений
При оценке микроускорений во внутренней среде космической лаборатории одним из главных факторов, порождающих поле микроускорений, считаются собственные колебания упругих элементов, возникающие после включения двигателей системы ориентации и управления движением КА (УРД) [1]. Работа УРД нарушает благоприятные условия для реализации гравитационно-чувствительных процессов, проводимых в лаборатории. Благодаря демпфированию собственных колебаний уровень микроускорений постепенно снижается ниже критического, позволяя проводить технологические процессы, поэтому от точности оценки времени начала реализации процесса зависит его успешное протекание. Таким образом, исследование влияния демпфирования собственных колебаний больших упругих элементов космической лаборатории на поле порождаемых микроускорений в ее внутренней среде является актуальной задачей.
Как правило, при учете демпфирования используется схема вязкого трения, а логарифмический декремент считается постоянным [2]. Данная оценка применима в случае, если космическая лаборатория не погружается в тень Земли. В настоящее время предполагаются именно такие орбиты, однако широкое освоение околоземного пространства и создание космических минизаводов склонит к использованию менее благоприятных орбит в целях безопасности эксплуатации
космической техники, поэтому задача рассмотрения полета космического аппарата (КА) с погружением в тень Земли также является актуальной. Строго говоря, значение логарифмического декремента зависит от многих факторов. Основными из них являются температура элемента, частота собственных колебаний и внутренней энергии деформации элемента [3]. Поскольку речь идет о небольших колебаниях [4], порождающих микроускорения во внутренней среде КА, температурные деформации вызывают отклонение порядка 0,20 [5], то внутренняя энергия деформации будет изменяться в небольших пределах. Следовательно, её влиянием на логарифмический декремент можно пренебречь. Статистический анализ, проведенный в [6], показывает, что хорошую оценку можно получить, учитывая только первую форму колебаний. Поэтому практическое значение имеет построение модели со случайным логарифмическим декрементом, зависящим от температуры.
В данной работе будет рассмотрен самый неблагоприятный сценарий движения космической лаборатории типа «НИКА-Т» по орбите, характеризующийся максимальным временем пребывания КА в тени Земли, а, следовательно, и перепадом температур больших упругих элементов. Такому сценарию соответствует нулевое наклонение орбиты. Следует сделать оговорку о том, что проектные параметры орбиты предполагали такое наклонение, которое обеспечивало бы отсутствие теневого участка в орбите КА [3]. Представим большие упругие элементы КА однородными ортотропными пластинами и рассмотрим уравнение теплопроводности в виде [4]:
Известия Самарского научного центра Российской академии наук, том 14, №1(2), 2012
8 T . 8 2 T cp^ = ^^ + qv ( t t) 8t 8 x
при граничных условиях:
—
, 8 T A--
8 x x = о x = l
= £a I T 4( x ; t )| x = о — Tc4 I x = l
где 2 - теплопроводность, с - удельная теплоемкость, р - плотность, е - интегральный коэффициент теплового излучения упругого элемента, о - постоянная Стефана-Больцмана, T ( x ; t )| x = 0 -
поле температур на поверхности пластины, Т с -
чем в остальные по причине того, что КА большую часть времени находится на освещённой части своей орбиты. При ненулевом наклонении орбиты эта неравномерность распределения будет еще ярче, поскольку время пребывания в тени уменьшится. Зависимость логарифмического декремента от температуры для материала МА2, из которого предполагалось изготавливать каркас для ПСБ, при минимуме внутренней энергии деформации для первой собственной формы колебаний представлена на рис. 3.
Выделим четыре фиксированных значения логарифмического декремента в интервале температур (рис. 1) от 0,07 до 0,1 с шагом 0,01, ко-
температура окружающей среды,
q v ( t) = — 2 ^^^ ( T 4(0; t) — Tc 4)
- локальная удельная
мощность тепловыделения элемента пластины.
Упрощенно считая, что мощность солнечной энергии, приходящейся на всю площадь упругого элемента, составляет 14 кВт на освещенной части орбиты и равна нулю на теневой, получим динамику температуры упругого элемента при движении КА по орбите (рис. 1).
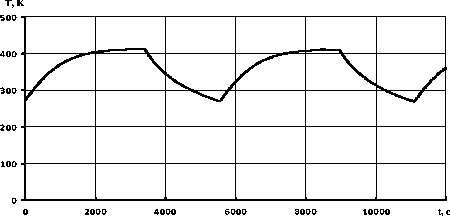
Рис. 1. Динамика температуры упругого элемента КА при движении по орбите
торые соответствуют данному температурному диапазону. Эти значения будут составлять гене-
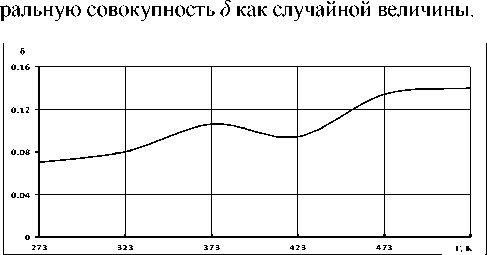
Рис. 3. Динамика логарифмического декремента первой формы собственных колебаний для материала МА2 [3]
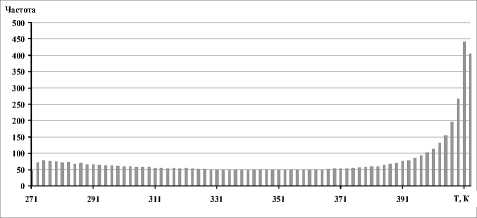
Рис. 2. Частота появления различных значений температуры упругого элемента
С помощью интервального метода, используя частоты появления различных значений температур (рис. 2) и зависимость логарифмического декремента от температуры, можно аппроксимировать закон распределения этой случайной величины (рис. 4). Тогда самым неблагоприятным с точки зрения микроускорений сценарием будет ситуация, когда УРД выключаются незадолго до выхода КА из тени. Если за начало отсчета времени выбрать точку выхода из тени, то такой сценарий реализуется при выключении УРД примерно на 4850 секунде полета по орбите. При этом наблюдается наименьшее значение логарифмического декремента (0,07) и, как следствие, колебания не затухают более продолжительный период времени.
Разобьем весь диапазон изменения температуры за один оборот КА вокруг Земли на отрезки А Т =2K, при этом будем фиксировать температуру упругого элемента каждую секунду. Воспользуемся интервальным методом для определения числа точек, оказавшихся в каждом из отрезков, и построим частоту появления различных значений температуры элемента, считая, что эти значения соответствуют серединам отрезков (рис. 2).
В целом закон распределения температур существенно неоднороден за счёт диапазона 390400 К, вероятность попадания в который выше,
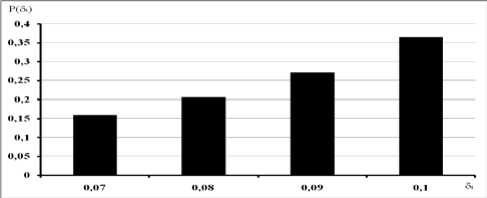
Рис. 4. Закон распределения логарифмического декремента
Самым благоприятным сценарием следует считать выключение УРД примерно на 2000 секунде полета, когда логарифмический декремент
максимален. Зависимости микроускорений для обоих сценариев приведены на рис. 5. Анализ рис. 5 показывает, что для самого неблагоприятного сценария требования по микроускорениям
(менее 20 мкм/с2, обозначено как критическое значение на рис. 5) выполняются спустя примерно 38 с после выключения УРД, а для самого благоприятного – спустя примерно 23 с.
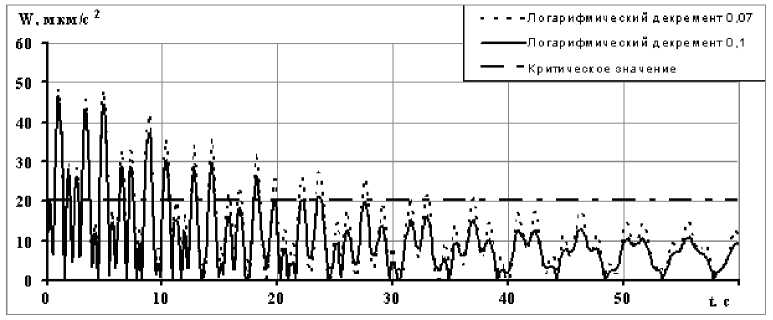
Рис. 5. Динамика микроускорений, порождаемых колебаниями ПСБ КА типа «НИКА-Т», при различных сценариях
Вывод: можно утверждать о существенном влиянии случайности логарифмического декремента на выполнение благоприятных условий микрогравитационного штиля в случае, когда орбита КА содержит значительные теневые участки.
Список литературы О законе распределения логарифмического декремента при моделировании микроускорений
- Березин, И.А. Расчет микроускорений на орбитальном комплексе «Мир»/И.А. Березин, В.В. Сазонов, В.И. Стажков//Труды XXV Чтений К.Э. Циолковского. -М., 1991. С. 22-31.
- Титов, Б.А. Формирование динамических свойств упругих космических аппаратов/Б.А. Титов, В.А. Вьюжанин, В.В. Дмитриев. -М.: Машиностроение, 1995. 304 с.
- Рассеяние энергии при колебаниях упругих систем/под ред. Г.С. Писаренко. -Киев: Наукова Думка, 1966. 304 с.
- Седельников, А.В. Оценка влияния температурных деформаций упругих элементов космической лаборатории на поле микроускорений ее внутренней среды/А.В. Седельников, В.В. Юдинцев//Известия Самарского научного центра РАН. 2011. Т. 13, № 1(2). С. 344-346.
- Johnston, J.D. Thermally induced attitude dynamics of a spacecraft with a flexible appendage/J.D. Johnston, E.A. Thornton//Journal of guidance, control and dynamics. 1998. Vol. 21, № 4. Р. 581-587.
- Седельников, А.В. Вероятностная модель микроускорений с постоянным логарифмическим декрементом//Известия Самарского научного центра РАН. 2011. Т. 13, № 4(4). С. 1022-1026.
- Седельников, А.В. Проблема микроускорений: от осознания до фрактальной модели. -М.: РАН, Избранные труды Российской школы по проблемам науки и технологий, 2010. 106 с.
- Тихонов, А.Н. Уравнения математической физики/А.Н. Тихонов, А.А. Самарский. -М.: Наука, 1977. 736 с.


