О законе распределения логарифмического декремента при наличии теневого участка орбиты космической лаборатории

Космическое материаловедение сегодня - быстроразвивающаяся передовая наука. Создаются новые технологии с использованием уникальных свойств космического пространства, главным из которых яв- ляется микрогравитация. Поле микроускорений, создаваемое во внутренней среде космического аппарата (КА) различными внешними и внутренними факторами, нарушает состояние полной невесомости и является серьезным препятствием для развития космических технологий [1]. Несмотря на то, что проблема создания благоприятных условий для успешной реализации гравитационно-чувствительных технологических процессов в космосе имеет более чем тридцатилетнюю историю [2], эффективного ее решения до сих пор не найдено.

Многочисленные замеры и оценки микроускорений на больших космических станциях (например, [3] на орбитальных комплексах «Салют-6, 7», [4] на орбитальной космической станции «Skylab», [5] на орбитальном комплексе «МИР», [6] на международной космической станции (МКС), [7] на станции «Тяньгун-1») показывают, что жесткие требования к уровню микроускорений, предъявляемые современными гравитационно-чувствительными процессами [8] (рис. 1), не выполняются.

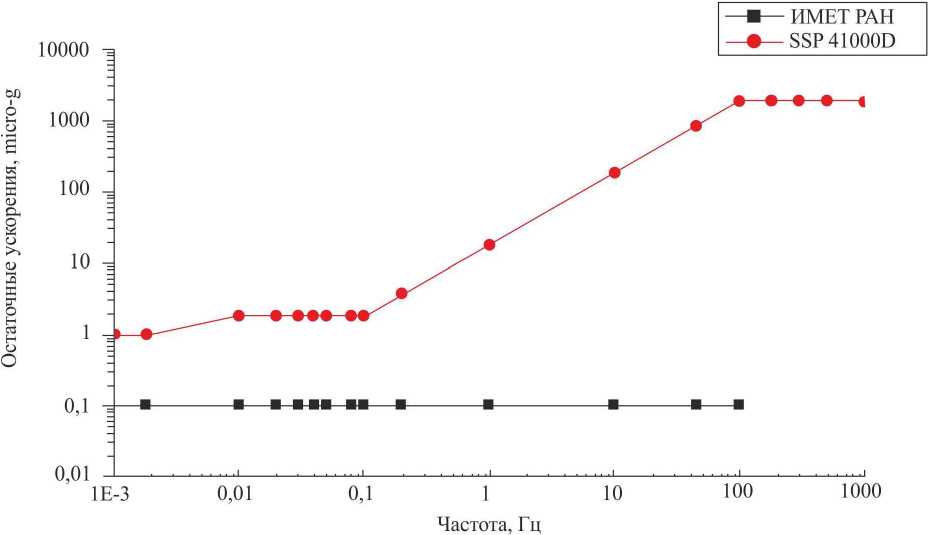
Рис. 1. Требования к уровню микроускорений для успешного проведения гравитационно-чувствительных процессов

Верхняя кривая на рис. 1 означает достаточный для многих гравитационно-чувствительных процессов уровень микроускорений, который оформлен в виде специального документа SSP 41000D.

Ежедневные упражнения экипажа также влияют на уровень микроускорений, создавая технологам дополнительные проблемы [9]. Эти проблемы можно решить двумя путями. Создать в составе орбитальной станции отдельный лабораторный модуль, используя при этом специальные устройства виброзащиты технологического оборудования. По этому пути пошли европейские и японские исследователи, запустив к МКС модули Columbus [10] и Kibo [11] соответственно. Технологическое оборудование на модуле Columbus защищает от чрезмерных микроускорений Microgravity Vibration Isolation Subsystem, разработанную на основе испытанного на орбитальном комплексе «Мир» виброзащитного устройства Microgravity Vibration Isolation Mount [12]. Аналогичное устройство ВЗП-1К было разработано и испытано российскими специалистами [13].

Этот путь позволяет использовать возможности больших космических станций, оперативно вмешиваться в работу технологического оборудования и проводить его своевременную диагностику, однако для серийного космического производства больше подходит второй путь, который заключается в создании специализированного беспилотного космического аппарата (КА) технологического назначения. Этот КА, с одной стороны, должен обеспечивать технологическое оборудование, а также вспомогательные системы достаточной для эффективной работы электрической мощностью, с другой - реализовывать низкий уровень микроускорений, необходимый для успешного протекания гравитационно-чувствительных процессов. Тогда он будет являться прообразом космического мини-завода будущего.

Существуют примеры КА с низким уровнем микроускорений. К таким КА можно отнести серию «Фотон» и Spot-4. Измерения микроускорений на КА «Фотон» (например, [14], [15] или [16]) наглядно демонстрируют, что на этих аппаратах реализуется самый низкий уровень квазистатической составляющей микроускорений. Происходит это из-за отсутствия в конструктивно-компоновочной схеме (ККС) больших упругих элементов (например, панелей солнечных батарей (ПСБ)). Однако, с другой стороны, это является существенным недостатком, поскольку без ПСБ срок активного существования на орбите этих аппаратов (всего запущено 17 КА серии) не превышает 18 суток [1]. Именно собственные колебания больших упругих элементов КА, возбуждаемые периодическими включениями двигателей системы ориентации и управления движением (УРД), являются основным источником квазистатической компоненты микроускорений [17].

Опыт работы КА Spot-4 показал, что при реализации низкоэнергоемких гравитационно-чувствительных процессов, например получе- ние четких снимков поверхности Земли с помощью космического телескопа, возможен ряд конструктивных решений, позволяющих существенно снизить вклад собственных колебаний ПСБ в поле микроускорений во внутренней среде КА. Единственная ПСБ Spot-4 крепилась к корпусу посредством упругого стержня. Благодаря чему колебания панели существенно не влияли на поле микроускорений [18]. Однако в такой ситуации нельзя выполнить жесткие требования к ориентации ПСБ на Солнце. Поэтому в случае высокой энергоемкости проводимых технологических процессов такой конструктивный прием недопустим.

Таким образом, при движении по второму пути необходимо создавать автономную энерговооруженную беспилотную космическую лабораторию с длительным сроком активного существования на орбите. В России разрабатывались три проекта таких лабораторий. В конце 80-х - начале 90-х годов прошлого века проектировался КА «НИКА-Т», срок активного существования которого оценивался в 120 суток [1]. Однако проект не был доведен до реализации. В настоящее время идет разработка двух проектов космических лабораторий: «ОКА-Т» [19] и «Фотон-М4», ККС которого уже содержит две ПСБ, благодаря чему срок активного существования увеличен до 90 суток [20]. Ближе всего к практической реализации находится проект «Фотон-М4», запуск которого запланирован на осень 2013 года.

Уровень микроускорений во внутренней среде космической лаборатории является одной из основных ее характеристик, поскольку именно он определяет, какие гравитационно-чувствительные процессы могут успешно протекать на КА. Поэтому без эффективного решения этой проблемы вряд ли стоит ждать значительного прогресса в области космического материаловедения.

1.    Постановка задачи

Рассматривается движение космической лаборатории, содержащей большие упругие элементы. Основным источником микроускорений считаются собственные колебания этих элементов, которые возбуждаются благодаря периодическому включению УРД. Все гравитационно-чувствительные процессы можно проводить в период между включениями УРД, поскольку сами двигатели создают недопустимо высокий уровень микроускорений [21]. Для увеличения этого периода разработан целый ряд различных решений, например использование электроракетного двигателя, препятствующего разориентации [22].

В такой постановке оценка микроускорений тесно связана с моделированием собственных колебаний. Если орбита КА не содержит теневых участков, то логарифмический декремент можно считать постоянным [23]. При наличии теневых зон температура ПСБ существенно изменяется. На рис. 2 показана зависимость температуры ПСБ от времени при движении КА типа «НИКА-Т» по орбите с нулевым наклонением [24].

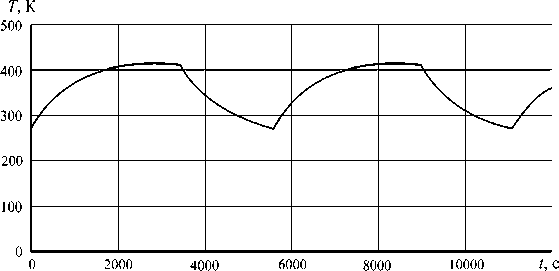
Рис. 2. Зависимость температуры ПСБ от времени

Зависимость логарифмического декремента от температуры для материала МА2, из которого предполагалось выполнить каркас ПСБ, приведена на рис. 3 [25].

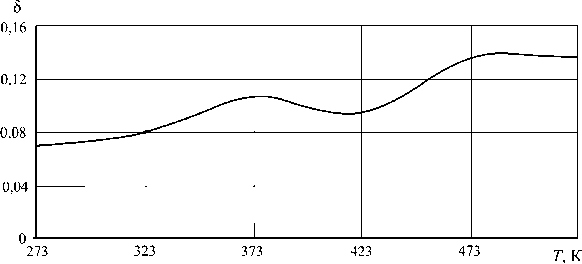
Рис. 3. Зависимость логарифмического декремента первой формы собственных колебаний пластины из сплава МА2 от температуры

Сравнивая два этих графика, можно констатировать, что при погружении КА типа «НИКА-Т» в тень логарифмический декремент нельзя считать постоянным.

В работе [24] рассмотрена самая «неблагоприятная» орбита с нулевым наклонением, содержащая наибольший теневой участок. Однако с практической точки зрения такая орбита вряд ли реализуема, а результаты исследования, представленные в работе, подтверждают актуальность данной задачи. Для полномасштабной картины необходимо исследовать закон распределения логарифмического декремента в зависимости от наклонения орбиты. Это и является целью данной работы.

2.    Результаты

В работе [26] получена зависимость температуры ПСБ от времени при различных значениях наклонения орбиты, а также установлено, что при наклонении орбиты i >  56 ° КА типа «НИКА-Т» в тень Земли попадать не будет. Поскольку заранее неизвестно, в какой точке орбиты произойдет включение УРД, значение логарифмического декремента на момент его выключения будет случайным. С помощью зависимостей, приведенных на рис. 2 и 3, установлено, что в рассматриваемой ситуации логарифмический декремент можно рассматривать как дискретную случайную величину с четырьмя различными значениями: 5 1 = 0,07; 5 ₂ = 0,08; 5 ₃ = 0,09; 5 ₄ = 0,10. Используя интервальный метод, в работе [26] был построен эмпирический закон распределения логарифмического декремента, приведенный на рис. 4.

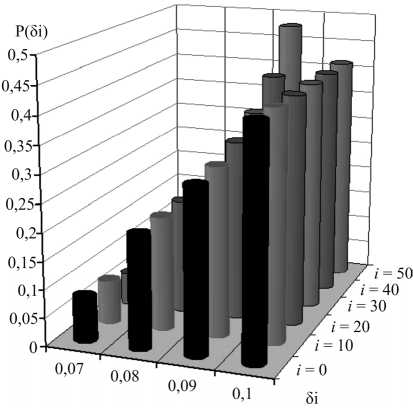
Рис. 4. Эмпирический закон распределения логарифмического декремента при различных наклонениях орбиты КА для высоты 400 км

При этом температура ПСБ фиксировалась каждую секунду, в результате чего получена выборка значений температур, соответствующая периоду обращения КА вокруг Земли. Для высот 200, 300, 400, 500 и 600 км объем этой выборки составляет соответственно 5301, 5421, 5544, 5667 и 5791 точек. Поэтому можно с уверенностью говорить о достаточности статистического материала для анализа закона распределения логарифмического декремента. Непрерывный отрезок изменения температур от 270 К до 440 К (см. рис. 2) был разбит на 72 диапазона, каждый из которых представлял собой изменение температуры на 2 К. Далее все точки выборок были распределены по 72 диапазонам. После этого каждому из 72 диапазонов изменения температуры было поставлено в соответствие одно из четырех значений логарифмического декремента (см. рис. 3), указанных выше, а сами диапазоны стали основой для распределения точек выборок по значениям логарифмического декремента. Затем была вычислена вероятность появления каждого из четырех значений логарифмического декремента путем отношения числа точек, соответствующих данному значению декремента, к общему числу точек выборки. Полученные результаты в виде диаграммы представлены на рис. 4 для различных наклонений орбиты и ее высоты 400 км.

Рассмотрим соответствие этого закона биномиальному распределению, выбрав в качестве критерия критерий согласия % ² Пирсона:

N т^т   _иэ

%2 = у (pi-1 - pi) %  ^   тт ,

i - I        p i - 1

где р т^ - теоретическая вероятность успеха в i -1 испытаниях, а p i -экспериментальная вероятность появления i -го значения логарифмического декремента.

Поскольку имеется четыре различных значения логарифмического декремента, число независимых испытаний Бернулли примем равным трем. Тогда значения логарифмического декремента 0,07, 0,08, 0,09 и 0,1 будут соответствовать числу успехов в трех независимых испытаниях 0, 1, 2 и 3. Считая вероятность успеха в каждом испытании р постоянной, подберем такое ее значение, которое соответствует минимальному значению критерий согласия %2 Пирсона (1). Таким образом, можно получить теоретическое биномиальное распределение, максимально соответствующее эмпирическому, для различных наклонений и высот орбит КА (рис. 5).

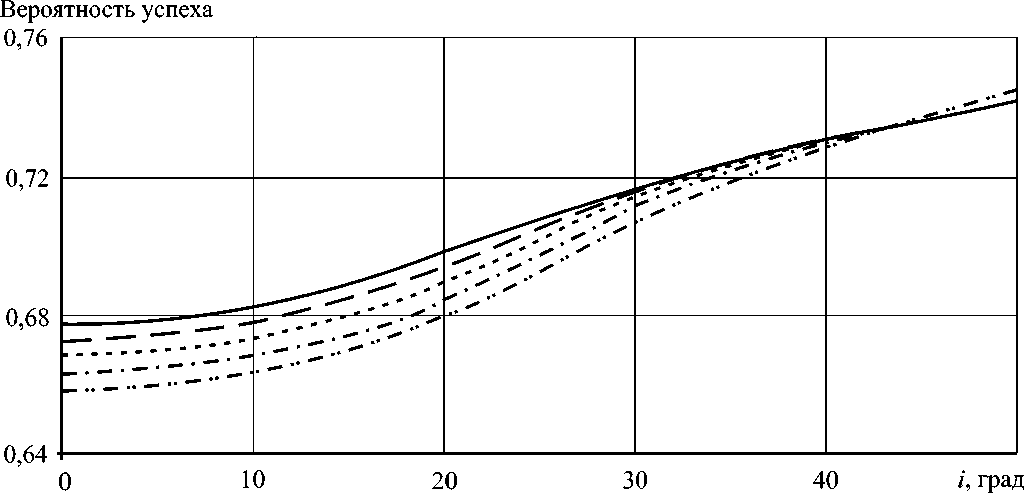
Рис. 5. Значение вероятности успеха при трех независимых испытаниях Бернулли

На рис. 5 кривые сверху вниз построены для 600, 500, 400, 300 и 200 км орбит КА соответственно. Различия между теоретическим и эмпирическим законами распределения, оцененные с помощью (1), показаны на рис. 6.

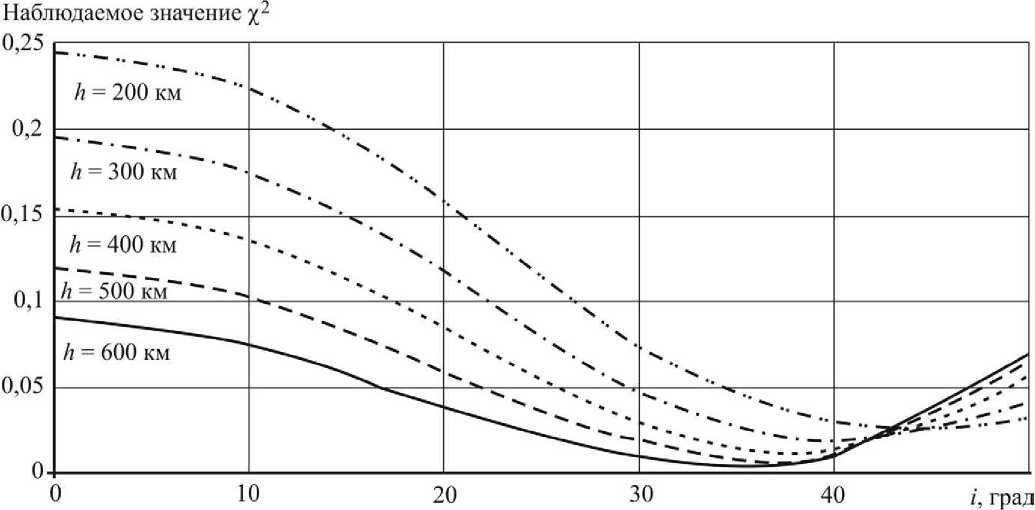
Рис. 6. Наблюдаемое значение критерия согласия / ² Пирсона при проверке гипотезы о биномиальном законе распределения логарифмического декремента

Критическое значение для 5%-го уровня значимости % 2_р = 3,84146. Очевидно, что гипотеза о соответствии эмпирического закона распределения биномиальному может быть принята на 5%-ном уровне значимости.

Таким образом, с помощью биномиального распределения можно аппроксимировать закон распределения логарифмического декремента для произвольных значений наклонения и высоты орбиты, используя зависимости, приведенные на рис. 5.

Выводы

Наличие теневого участка орбиты вызывает дополнительные трудности, связанные с тепловым ударом, который испытывают ПСБ при погружении и выходе из тени Земли [27] и, как следствие, появление дополнительных микроускорений, связанных с этим ударом.

Перепад температур не позволяет считать логарифмический декремент собственных колебаний постоянным для таких материалов, как МА2, из которого предполагалось изготовление каркаса ПСБ для КА «НИКА-Т». Для других материалов необходимо проводить дополнительные исследования, чтобы убедиться в выполнении наложенных на модуль микроускорений ограничений.

Представленные в работе результаты исследований наглядно демонстрируют необходимость усложнения модели для адекватной оценки микроускорений при наличии теневого участка орбиты. Пренебрежение случайностью логарифмического декремента может привести к существенным ошибкам. Так, использование рекомендуемого в работе [28] значения логарифмического декремента для первой собственной формы колебаний 0,1 приведет к тому, что допустимый модуль микроускорений для КА типа «НИКА-Т» 20 мкм/с2 [1] будет достигнут спустя приблизительно 23 с после выключения УРД. Однако при включении УРД на теневом участке орбиты может привести к снижению этого значения до 0,07, что означает достижение допустимого уровня микроускорений только примерно через 38 с (рис. 7) [24]. Такие ошибки более чем на 65 % могут привести к неудачному завершению гравитационно-чувствительных процессов.

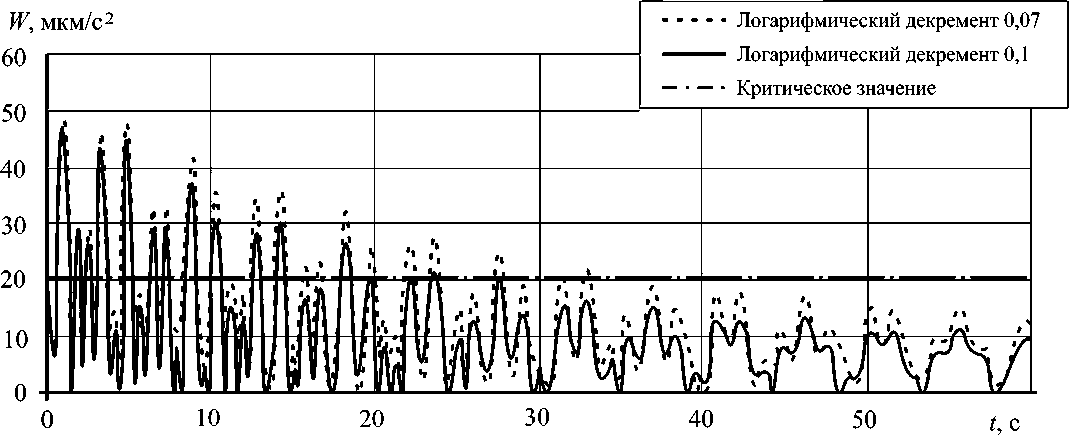
Рис. 7. Зависимость микроускорений от времени для КА типа «НИКА-Т» после выключения УРД для различных значений логарифмического декремента

Результаты проведенной работы могут быть использованы при оценке микроускорений на борту космической лаборатории, а также подбора параметров орбиты, обеспечивающих выполнение заданных условий по микроускорениям.