О законе распределения времени торможения ленточных конвейеров

• -    датчик, подающий сигнал на отключение привода и включение тормоза конвейера;

• -    электроаппаратуру, которая по сигналу датчика выключает привод конвейера и включает тормоз;

• -    тормоз конвейера (обычно колодочный или какой-либо другой фрикционный).

Эффективность применения системы аварийного останова ленточного конвейера определяется временем ее срабатывания – временем от момента подачи сигнала датчиком до окончания остановки конвейера:

tC= tд + tа + tT, с, где tд – время срабатывания датчика; tа – время срабатывания электроаппаратуры управления тормозом; tT – время торможения от момента включения тормоза до полной остановки конвейера.

Для точного определения t C и места установки датчика все величины, входящие в уравнение, следует рассматривать как случайные, независимые, описываемые своими законами распределения. Согласно [1], ток срабатывания датчика и электроаппаратуры управления тормозом подчиняется закону нормального распределения. Поскольку ток срабатывания и время срабатывания связаны между собой функциональной зависимостью, то можно полагать, что и время срабатывания также будет распределено по нормальному закону.

Закон распределения времени t T по аналогии зачастую также считают нормальным, однако в работах [2, 3] показано, что закон распределения вероятностей тормозного пути при воздействии сил трения равномерный. Это позволяет предполагать, что и время t T распределено равномерно.

Цель исследований . Определение закона распределения времени торможения ленточного конвейера от момента включения тормоза до полной его остановки.

Материалы и методы исследований. В качестве экспериментальной установки использовался ленточный конвейер 1 (рис. 1) длиной 54 м, шириной ленты 650 мм, диаметром барабана 630 мм. Установка снабжена следующими узлами: 2 – редуктор РМ-400; 3 – колодочный тормоз ТКТГ-300 с электрогидравличе-ским толкателем; 4 – двигатель АО63–6 (скорость вращения 980 об/мин); 5 – тахогенератор ЭТ-7, жестко соединенный с валом двигателя; 6 – быстродействующий самопишущий прибор Н-327 с разрешающей способностью 10-3 с. При отключении конвейера и включении тормоза скорость вращения двигателя меняется синхронно со скоростью конвейера. Это позволяет, записывая сигналы от тахогенератора, получить представление о процессе и времени торможения tT (рис. 2). Зная скорость движения ленты самописца VЛ (опыты проводились при VЛ = 50 мм/с), измерив расстояние АВ от точки Н (начало торможения) до точки К (конец торможения), получали время торможения конвейера с момента включения тормоза до полной остановки конвейера.

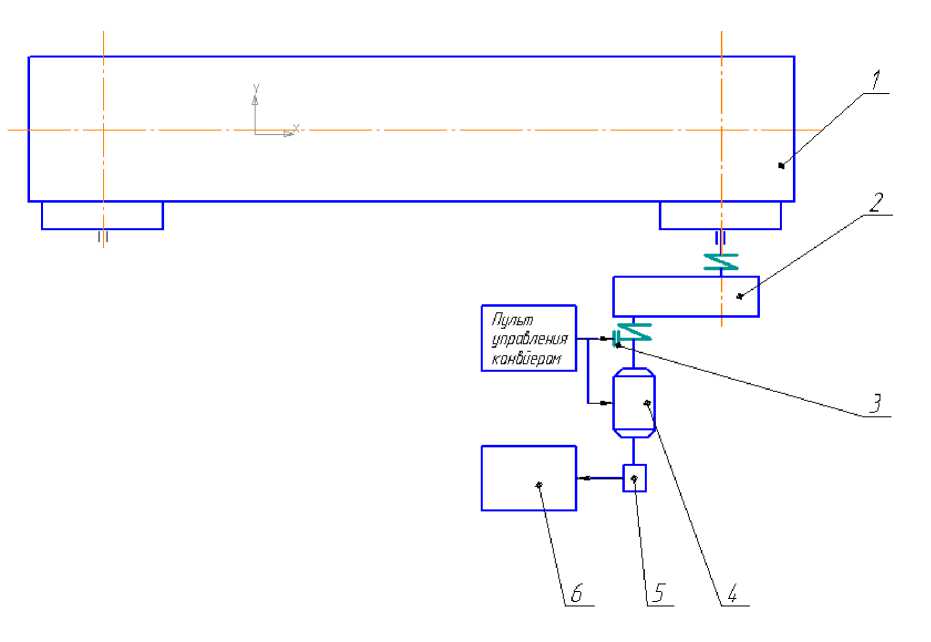
Рис. 1. Схема экспериментальной установки для проверки гипотезы о законе распределения времени торможения ленточного конвейера: 1 – ленточный конвейер; 2 – редуктор РМ-400; 3 – тормоз ТКТГ-300;

4 – двигатель АО63-6; 5 – тахогенератор; 6 – самопишущий прибор Н-327

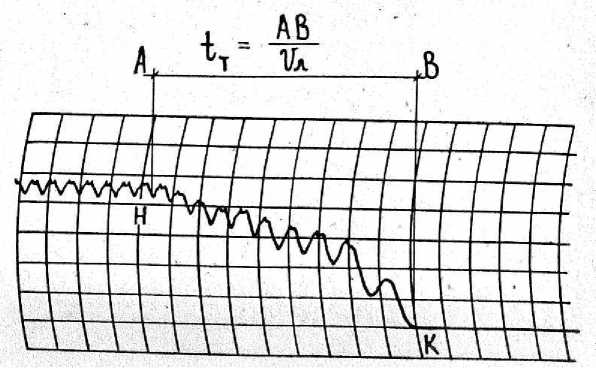
Рис. 2. Пример записи процесса торможения ленточного конвейера:

Н и К – соответственно начало и конец процесса торможения; V Л – скорость торможения

Результаты исследований и их обсуждение . С помощью описанной установки и нескольких аналогичных ей, построенных на базе других конвейеров, были получены экспериментальные значения t T . Некоторые результаты замеров для установки приведены в табл. 1.

Таблица 1

Время торможения ленточного конвейера от момента включения тормоза до полной остановки

№ п/п	t T , с	№ п/п	t T , с	№ п/п	t T , с	№ п/п	t T , с	№ п/п	t T , с
1	0,76	11	0,84	21	0,96	31	0,81	41	0,83
2	0,90	12	0,86	22	0,95	32	0,77	42	0,77
3	0,88	13	0,75	23	0,83	33	0,77	43	0,90
4	0,78	14	0,78	24	0,83	34	0,90	44	0,95
5	0,84	15	0,78	25	0,83	35	0,77	45	0,95
6	0,86	16	0,92	26	0,87	36	0,83	46	0,79
7	0,86	17	0,87	27	0,91	37	0,95	47	0,83
8	0,88	18	0,78	28	0,76	38	0,80	48	0,95
9	0,88	19	0,76	29	0,86	39	0,97	49	0,83
10	0,78	20	0,84	30	0,96	40	0,80	50	0,98

Обработка экспериментальных данных состояла в следующем:

• а)    проверка выборочной совокупности данных на репрезентативность;

• б)    построение гистограмм выборочного распределения значений;

• в)    проверка гипотезы о равномерном законе распределения времени торможения ленточного конвейера.

Проверка выборки на репрезентативность проводилась с использованием способа числа и длины серий [4]. Вначале определяли среднее значение времени торможения конвейера по экспериментальным данным, t TСР = 0,847 с (для данных табл. 1). Затем ряд значений t T в порядке получения выборки представляли в виде последовательности символов «+», если t T > t TСР и «–«, если t T < t TСР , и далее находили наибольшую длину К Н серий «+» и «–» и общее число серий К Н . Полученные значения К Н = 4 и R Н = 26 (для табл. 1) сравнивали с критическими значениями (К = 9 и R = 19). Результаты сравнения К Н < К и R H > R [4] позволяли считать все выборки репрезентативными.

Расчет критерия Пирсона χ²

Таблица 2

t T	f I	f I '	(f I – f I ')	(f I – f I ')2	(f I – f I ')2/f I
0,75–0,78	8	6,28	1,72	2,96	0,47
0,78–0,81	9	6,28	2,72	7,40	1,18
0,81–0,84	8	6,28	1,72	2,96	0,47
0,84–0,87	6	6,28	0,28	0,078	0,01
0,87–0,90	6	12,56	2,56	6,55	0,55
0,90–0,93	4	-	-	-	-
0,93–0,96	5	12,56	3,56	12,67	1,01
0,96–0,99	4	-	-	-	-

Для построения гистограммы распределения весь диапазон экспериментальных значений t T был разбит на интервалы по 0,03 с, после чего были определены частоты попадания значений в каждый интервал. По частотам и интервалам построены гистограммы, внешний вид которых подтверждает гипотезу о равномерном распределении t T , однако для более глубокой ее проверки целесообразно воспользоваться критерием Пирсона χ². Для данных табл. 1 и равномерного закона распределения f I ' = const = 6,28. Значения f I приведены в табл. 2, где эмпирическое значение критерия Пирсона χ² = = 3,59. Число степеней свободы:

• k = m – p – 1,

где p = 2 – число параметров закона равномерного распределения; m = 6.

Заключение . В соответствии с [4] для полученных значений χ² и k вероятность Р приближенно равна 0,33. Критическое же значение этой вероятности, при которой гипотеза должна быть отвергнута, составляет 0,05. Поскольку Р (χ²) > 0,05, правомерно считать, что закон распределения времени торможения ленточного конвейера от момента включения тормоза до полной остановки равномерный.