О замыкании электростатическим уравнением системы зависящих от времени уравнений массопереноса вещества в электропроводящих жидких растворах
Автор: Шарфарец Борис Пинкусович, Шарфарец Е.Б.
Журнал: Научное приборостроение @nauchnoe-priborostroenie
Рубрика: Математические методы и моделирование в приборостроении
Статья в выпуске: 2 т.25, 2015 года.
Бесплатный доступ
Приведены условия правомерности замыкания системы зависящих от времени уравнений массопереноса в растворе электролита электростатическим уравнением. Показано, что этим уравнением должно быть уравнение Пуассона с соответствующими значениями плотности заряда в дискретные моменты времени. Отмечено, что его замена условием электронейтральности является некорректной. Приведены зависимости некоторых параметров массопереноса от температуры.
Уравнение пуассона, уравнение навье, стокса, уравнение нернста, планка, уравнение теплопереноса, условие электронейтральности
Короткий адрес: https://sciup.org/14264978
IDR: 14264978 | УДК: 544.62
Текст научной статьи О замыкании электростатическим уравнением системы зависящих от времени уравнений массопереноса вещества в электропроводящих жидких растворах
Описание процесса переноса вещества в жидкостях представляет собой непростую задачу, сводящуюся к связанной системе различных уравнений, позволяющих определять все поля, необходимые для решения этой проблемы. Например, в работе [1, с. 335, 336] для случая процессов переноса в разбавленных растворах (простейшая из подобных задач) представлена система, состоящая из уравнения Нернста—Планка для потока растворенных компонентов, уравнения материального баланса, условия электронейтральности, уравнения плотности тока и системы уравнений Навье—Стокса для несжимаемой жидкости. В работах [2, 3] к этим уравнениям добавлено уравнение теплопереноса, а вместо условия электронейтральности приведено уравнение Пуассона, связывающее электрический потенциал с плотностью электрического заряда.
В описанной системе уравнений присутствует исходное противоречие, связанное с тем, что часть уравнений системы (уравнения материального баланса, Навье—Стокса и теплопереноса) существенно зависят от времени, а, например, уравнение Пуассона или условие электронейтральности являются статичными. Кроме того, возникает вопрос, какое из уравнений (Пуассона или электронейтральности) в условиях отмеченного противоречия использовать в качестве замыкающего уравнения для определения электрического потенциала.
Решению этих проблем, а также ряду других вопросов посвящена настоящая работа.
УРАВНЕНИЯ ЭЛЕКТРОСТАТИКИ, ПРИНЯТЫЕ В ЭЛЕКТРОКИНЕТИЧЕСКИХ ПРОЦЕССАХ
|
В дальнейшем изложении опираемся на уравнения Максвелла [ 4, с. 16, 19 ] |
|
|
Vx E + — = 0, б t |
(1) |
|
Vx H - —= J , 6 1 |
(2) |
|
V- B = 0, |
(3) |
|
V- D = p. |
(4) |
Здесь E , H — вектора электрической и магнитной напряженности, а D и B — вектора электрической и магнитной индукции соответственно; J — вектор плотности тока; ρ — плотность электрического заряда.
Дифференциальное уравнение [ 1, с. 18 ]
V-J + ^ = 0
5 t
выражает закон сохранения заряда в окрестности какой-либо точки, или уравнение непрерывности (по аналогии с гидродинамикой). Оно получается путем воздействия оператором дивергенции на уравнение (2)
V- J + — V- D = 0
при учете соотношения (4).
В изотропной среде существует связь между векторами E и D [ 4, с. 23 ]
D = ее o E , (7)
где е 0 = 8.85 - 10 - 12 Кл2 / (Н - м2) = 8.85 - 10 - 12 Ф/м — электрическая постоянная; ε — относительная диэлектрическая проницаемость среды, являющаяся функцией координат (при е = const — среда однородная, а в случае анизотропной среды ε — тензор).
В широком диапазоне условий как в случае твердых тел, так и в случае слабо ионизированных растворов полагается справедливым линейное соотношение (закон Ома) [ 4, с. 26 ]
J = ст E , (8)
где σ — удельная проводимость среды. В этом случае из уравнения непрерывности (5) и выражения (8) следует выражение [ 4, с. 27 ]
V- J + ^ = V- ( ct E U^ = 0, 5 t v ! е t
из которого при условии однородности среды ( ст = const) и учете выражений (4) и (7) следует уравнение [ 4, с. 27 ]
6р- + -р- = 0
d t ее 0
с решением
ρ el
( t ) = P 0 exp |- I , I т )
εε где т = —0 — время релаксации заряда. Во всех даже плохих проводниках τ достаточно мало. Так, в морской воде время релаксации порядка т = 2 -10-10 с; даже в таком плохом проводнике, как дистиллированная вода, оно не более 10-6с. В лучших изоляторах оно может тем не менее превышать величину 106 с [4, с. 27]. В зависимости от соотношения величин τ и t различают область, в которой необходимо изучать процесс. При т >> t, очевидно, справедливо приближение электростатики.
Подчеркнем, что уравнение (10) и его решение (11) справедливы в случае, когда имеет место закон Ома (8). Однако в случае жидкостей закон (8) вследствие различных явлений переноса, как правило, не выполняется. Это может происходить из-за наличия диффузии или конвекции [1, с. 243], и, как будет очевидно далее, закон (8) остается справедливым лишь при условии отсутствия конвекции и при однородной концентрации ионов.
Уравнения электростатики получаются непосредственно из уравнений Максвелла (1–4), если все производные по времени положить равными нулю. Далее будем иметь дело только с электромагнитными явлениями в электростатическом режиме и без учета каких-либо магнитных эффектов и эффектов излучения. Тогда система приведенных выше уравнений сводится к уравнениям (1) в форме (12), (4) и (7) [ 5, с. 141 ] :
Vx E = 0, (12)
V- D = V- ( ее 0 E ) = р ,
D = ее 0 E .
В [ 5, с. 141 ] к приведенным уравнениям добавлено еще уравнение (8), несправедливое в случае наличия диффузии и конвекции, которое заменится далее другим, учитывающим это влияние соотношением.
С учетом статичности процесса закон сохранения заряда (5), очевидно, должен быть записан так:
V-J = 0.(5а)
Следствием (12) является потенциальность поля вектора электрической напряженности
E = -Vф,(13)
а следствием (4) в случае однородности среды является уравнение Пуассона
Аф = - Р.(14)
МАССОПЕРЕНОС В РАСТВОРЕ ЭЛЕКТРОЛИТА
Далее рассмотрим указанную в заголовке раздела тему несколько более подробно, чем в предыдущей работе авторов [ 2 ] .
Описание массопереноса в растворе электролита освещает такие вопросы, как движение ионов, баланс вещества, электрический ток, электронейтральность и вопросы механики жидких сред. Среда полагается состоящей из неионизированно-го растворителя, электролита в виде ионов и незаряженных компонентов. Рассмотрим растворы при слабой концентрации растворенных компонентов (сильно разбавленные растворы).
Вектор потока каждого из растворенных компонентов описывается соответствующим уравнением Нернста—Планка [ 1, с. 245 ] :
N а =- Z a U a F C c V Ф - D a V С а + С а V • (15)
Здесь размерность N a — моль/ ( м 2 с ) ; v — вектор скорости жидкой смеси в целом; c α , моль м3 , — соответствующая концентрация α -компоненты; D α , м2 с, — коэффициент диффузии; u α , м2 • моль/ ( Дж • с ) , — подвижность ионов; za — заряд иона вида α в единицах заряда протона (безразмерная величина, равная валентности иона с учетом знака его избыточного заряда); F — число Фарадея.
Как видно из (15), N α есть вектор плотности потока вещества α -компоненты, складывающийся из трех векторов плотностей потоков:
– вектора миграции (первое слагаемое справа в (15)), вызванного воздействием электрического поля (в случае отсутствия ионов миграционная составляющая равна нулю);
– вектора диффузии (второе слагаемое справа в (15)), вызванного молекулярной диффузией за счет градиента концентрации соответствующей компоненты;
– вектора конвекции (третье слагаемое справа в (15)), вызванного объемным движением среды.
Плотность тока в растворе электролита обусловлена движением заряженных компонент [ 1, с. 246 ]
J = FZ Za Nа , α или после подстановки в последнее выражение уравнения (15)
J = F Z ( - z a U a Fc J ^ Ф - Z a D a ^ C a + Z « C a V ) = α
= C E - F Z z a D a V c a + F v Z z a c a , (16)
αα где с = F2 ZzauaCa — удельная проводимость рас-α сматриваемой жидкости. В случае электронейтральности раствора справедливо соотношение [1, с. 247]
Z Z a C a =0, (17)
α и выражение (16) приводится к виду
J = с E - F Z z a D « V C a . (16а)
α
Как видно из выражений (16), (16а), закон Ома в виде (8) справедлив только в случае отсутствия концентрационных градиентов ионов и в отсутствие конвекции, а в случае выполнения условия электронейтральности (17) справедлив только при равновесной концентрации ионов. В противном случае необходимо пользоваться более сложными законами (16), (16а) соответственно.
Величина заряда легко определяется из соотношения [ 1, с. 261 ]
Р = F Z Z a C a . (18)
α
С учетом этого уравнение Пуассона (14) перепишется в виде
F
А ф = - Z z a c a . (19)
εε 0 α
Далее понадобится условие материального баланса для каждой составляющей [ 1, с. 246 ]
до „
— = -V^ N + R = αα д t
= -V^ ( - Z a U a F C a V ф - D a V C a + C a V ) + R a , (20)
где R α — источник, обусловленный гомогенной химической реакцией. При умножении уравнения (20) на z α F и суммировании по компонентам α получается выражение
^1 F Z Z a C a I = -V^| f Z Z a N a ) + F Z Z a R a . (21) д t \ a j \ a j a
Если все гомогенные реакции, дающие вклад в R α , электрически сбалансированы или равны нулю, то последний член в (21) равен нулю. Выражение слева есть скорость изменения плотности заряда (18), а первый член справа есть дивергенция плотности тока (16) с обратным знаком. С учетом этого (21) переписывается в виде, совпадающем с уравнением (5)
-
д Р = -V^ J . (22)
д t
При выполнении условия электронейтральности плотность заряда (18) тождественно равна нулю, и из последнего уравнения получается выражение [ 1, с. 251 ]
-
V^ J = 0. (23)
Отметим, что (23) совпадает с законом сохранения заряда в статическом случае (5а).
Очевидно, что решение уравнения (22) с плотностью тока (16а) не столь тривиально, как решение (11) уравнений (5), (8).
Здесь следует отметить [6, с. 114], что в отсутствие градиентов концентрации стабильно не может существовать ситуация, когда плотность заряда отлична от нуля. Более того, если каким-либо образом в системе возникает плотность зарядов, отличная от нуля, то время, необходимое для исчезновения заряда (а фактически для его переноса к границам системы), совпадает с упомянутым выше временем электрической релаксации заряда τ и имеет порядок наносекунд. Тем не менее известно [6, с. 114], что наличие концентрационного градиента и конвекции в растворе многократно увеличивает время релаксации заряда τ , определенного выше в (11) для случая выполнения закона Ома (8), т. е. без учета двух дополнительных слагаемых справа в (16а). Более того [6, с. 83], "малые скорости перемещения (заряженных, прим. авт.) частиц в растворе оправдывают использование электростатического уравнения Пуассона для связи электрического потенциала с плотностью заряда". Этот факт и позволяет в конечном итоге пользоваться электростатическим приближением.
Замечание 1 (см. [ 1, с. 248 ] ). Справедливость уравнения (15) в случае концентрированных растворов нарушается потому, что миграционный и диффузионный потоки должны определяться по отношению к некоторой средней скорости жидкости ( v в уравнении (15)), которая совпадает со скоростью растворителя в разбавленных растворах. В концентрированных растворах эта скорость не совпадает со скоростью растворителя, которая является лишь частью средней скорости. Кроме того, в уравнении для потока (15) рассматривается взаимодействие только между растворенными компонентами и растворителем, тогда как взаимодействие между растворенными компонентами не учитывается. Наконец, движущей силой для диффузии должен быть градиент активности; градиенты активности совпадают с градиентами концентрации лишь в крайне разбавленных растворах. Эти трудности можно обойти, используя уравнение многокомпонентной диффузии (формула [ 1, с. 269, (78.1) ] ). Тем не менее можно пользоваться и уравнением (15), поскольку оно правильно отражает сущность физических процессов. Следует лишь помнить, что уравнение (15) строго обосновано только в случае разбавленных растворов [ 1, с. 249 ] .
УРАВНЕНИЕ ПУАССОНА ИЛИ УСЛОВИЕ ЭЛЕКТРОНЕЙТРАЛЬНОСТИ ?
В динамической системе уравнений материального баланса (сохранения массы), каковой в случае разбавленных растворов является система (20), кроме полей концентраций ca (x,t), а = 1,2,...,N, фигурируют по крайней мере еще два меняющихся во времени поля: поле скоростей v(x, t) и поле потенциала ф(x,t). Поле скоростей вычисляется через уравнение движения Навье—Стокса, а с полем потенциала, зависящего от времени, дело об- стоит несколько сложнее. Прямое применение электростатического уравнения Пуассона (14), (19) требует обоснования, т. к. в этом случае потенциал электрического поля ф( x, t) необходимо вычислять из полной системы уравнений Максвелла (1)–(4). Однако, как было отмечено выше, когда время релаксации зарядов достаточно велико и, следовательно, поля их концентрации, а потому и электрический потенциал медленно меняются во времени, речь может идти об электростатическом приближении.
Отметим вместе с тем, что в литературе имеется некоторая неоднозначность по поводу того, какое уравнение, описывающее поведение электрического потенциала, использовать в качестве замыкающего уравнения в упомянутой динамической системе уравнений: электростатическое уравнение Пуассона (14), (19) или условие электронейтральности (17). Так, в работе [ 1, с. 247 ] в качестве замыкающего уравнения предлагается использовать условие электронейтральности (17), а несколько дальше в этой же работе [ 1, с. 261 ] отмечено, что "условие электронейтральности (17) нельзя считать фундаментальным законом природы. Более точным является уравнение Пуассона". Примерно так же сказано и в работе [ 6, с. 84 ] . В частности, и в работах [ 2, 3 ] предлагалось в качестве замыкающего уравнения использовать уравнение Пуассона. Рассмотрим далее этот вопрос подробнее.
Здесь отметим, что применение условия электронейтральности исключает применение уравнения Пуассона (19), т. к. последнее при выполнении условия электронейтральности (17) мгновенно трансформируется к уравнению Лапласа.
Рассмотрим, при каких физических условиях, помимо условия электронейтральности, электрический потенциал в растворе электролита удовлетворяет уравнению Лапласа.
Выпишем вначале, при каких физических условиях осуществляется переход к уравнению Лапласа от уравнения Пуассона.
Во-первых, при выводе уравнения Пуассона (14), (19) используется приближение — однородность среды растворителя применительно к диэлектрической проницаемости, т. е.
ее 0 = const.
Во-вторых, принимается само условие электронейтральности (17)
Z Z a C a = 0. α
И, наконец, в-третьих, (по умолчанию) должно выполняться выражение (5а) для закона сохранения заряда в электростатическом приближении как статический вариант общего закона сохранения заряда (5)
-
V- J = 0.
Выявим условия перехода к уравнению Лапласа без привлечения уравнения Пуассона. Рассмотрим разбавленный электролит, поведение которого описывается приведенными выше уравнениями (15)–(17) и (20). Проведем следующую цепочку рассуждений. Примем справедливым условие электронейтральности (17). Тогда выражением для плотности тока будет уравнение (16а). Следуя [ 1, с. 251 ] , подставим уравнение (16а) в уравнение (23), что дает
V-(aVф) + F^ZaV-(DaVCa ) = 0. (24)
α
В отсутствие концентрационных градиентов и при однородной удельной проводимости ст = F2 EzXuaca = const это уравнение преобразует-α ся к уравнению для электрического потенциала
А ф = 0, (25)
-
т. е. в области с однородным составом потенциал удовлетворяет уравнению Лапласа.
Для получения этого результата необходимо было правомерно перейти от уравнения (21) последовательно к уравнению (22), а затем к уравнениям (23), (24), а затем к уравнению Лапласа (25). При этом были приняты допущения:
– все гомогенные реакции, дающие вклад в R α , электрически сбалансированы или равны нулю (при переходе от уравнения (21) к (22))
F E z a R a = 0; α
– справедливо условие электронейтральности (17) (при переходе от уравнения (22) к уравнениям (23), (24))
E Z a C a = 0; α
– выполняется условие однородной удельной проводимости в объеме раствора
C = F 2 E z a U a c a = COnSt; α
– отсутствуют концентрационные градиенты
V c a = 0, a = 1,2,..., N
(при переходе от уравнения (24) к уравнению Лапласа (25) для электрического потенциала).
Отметим также, что условие электронейтральности (17), делая избыточным дифференцирование по времени плотности заряда, напрямую трансформирует общий закон сохранения заряда (22) к его статическому варианту (23), т. к. плотность заряда (18) в этом случае тождественно равна нулю.
На основе проведенного анализа можно сделать следующие выводы.
– Уравнение Пуассона и условие электронейтральности, описывая статическое состояние электрического поля, разнятся тем, что уравнение Пуассона допускает наличие распределения плотности электрического заряда, отличной от тождественного нуля; условие электронейтральности допускает распределение плотности электрического заряда, только тождественно равное нулю.
– Выполнение условия электронейтральности автоматически трансформирует уравнение Пуассона к уравнению Лапласа.
– Условие электронейтральности ведет к трансформации закона сохранения заряда (5), (22) к его статическому варианту (5а), (23) не потому только, что плотность заряда неизменна во времени (как в случае уравнения Пуассона), а и потому еще, что тождественно равна нулю.
– Условия правомерности перехода от уравнения Пуассона к уравнению Лапласа в случае рассмотрения раствора электролита напрямую менее обременительны, чем по цепочке равенств (20)– (25).
Если бы не некоторые различия в переходе к уравнению Лапласа, то можно было бы сказать, что условие электронейтральности соответствует уравнению Лапласа как частный случай уравнения Пуассона при плотности заряда, равной нулю.
Поскольку система уравнений материального баланса (20) является нестационарной во времени, то совершенно очевидно, что тесно связанная с концентрацией зарядов плотность электрических зарядов также будет нестационарной во времени. Поэтому, когда реальное время релаксации зарядов с учетом концентрационных градиентов и конвекции достаточно велико, условие электронейтральности абсолютно неприемлемо в качестве замыкающего уравнения. В качестве такового тогда необходимо использовать уравнение Пуассона. Поскольку оно является статическим уравнением, в его правой части должны фигурировать только функции пространственных координат — дискретные по времени отсчеты зависимости плотности электрического заряда, предварительно рассчитанные из уравнений материального баланса, где фигурирует электрический потенциал, рассчитанный на предыдущем временнóм шаге. При этом должны быть заданы начальные условия для концентраций. Если система в начальный момент времени находится в стационарном состоянии равновесия, то в качестве исходной начальной концентрации может быть использована статическая концентрация Больцмана, принятая при описании двойного электрического слоя в стационарном состоянии [1, 5].
Отметим также, что наличие значительных реальных величин времени релаксации способствует выполнению условия справедливости статического приближения, оправдывающего применение уравнения Пуассона.
Замечание 2. Учитывая, что в качестве замыкающего уравнения необходимо в общем случае выбирать уравнение Пуассона (14), (19), а не условие электронейтральности (17), при рассмотрении закона сохранения заряда (22) плотность тока необходимо определять в виде (16), в котором условие электронейтральности не выполняется.
Отметим также, что решение уравнения Пуассона с произвольной правой частью может быть проведено численно с помощью изложенной в [3] методики.
ТЕРМОЗАВИСИМОСТЬ НЕКОТОРЫХ ВЕЛИЧИН
В процессах переноса существенную роль играет зависимость параметров среды и, как следствие, самих физических полей от вариации температуры. В настоящем разделе рассмотрим термозависимость некоторых важнейших параметров.
Вязкость
Обычно в процессах переноса жидкость полагается несжимаемой. Движение несжимаемой жидкости определяется только сдвиговой вязкостью. Для большинства жидкостей зависимость сдвиговой вязкости от температуры T при постоянном давлении в узком интервале температур можно описать формулой Андраде [ 7, с. 374 ]
П = A ( T ) exp ^ T J . (26) A ( T ) по сравнению с экспонентой exp ^^ — слабая функция от T . В нулевом приближении B = W / k, где W — энергия активации молекулярного скачка; k — постоянная Больцмана. Таким образом, приближенно последняя формула перепишется так
_ Г W ) п = C exP I kT J, где C = A (T0); T0 — некая температура в рас- сматриваемом интервале температур. Величины C и W варьируются в зависимости от вида жидкости. Формулу Андраде рассматривают как эмпирическую [7, с. 374].
В работе [ 5, с. 106, 108 ] выражение (26) несколько детализировано
П = k T- 1 exp
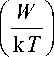
(26а)
где c 1 — константа, соответствующая конкретной жидкости.
Коэффициенты диффузии
Температурная зависимость ионных коэффициентов диффузии приближенно выражается соотношением [ 1, с. 261 ]
Dη
—— = const, T где η — вязкость раствора.
Если в последнее выражение подставить (26а), то получается выражение с W )
Da = -а T = C exp-- а , а П а ( R T )
совпадающее примерно с выражением в [ 8 ] . Здесь W α — соответствующая энергия активации; C α — константа, зависящая от конкретного вещества.
Дебаевская длина
Дебаевская длина — эффективная толщина диффузного слоя двойного электрического слоя (ДЭС). Эта величина также зависит от температуры [ 1, с. 97 ]
Г л ssoR T
1/2
X =
F 2Yz2c
F ^ z a c a 0
V a J
= C
λ
T 1/2
Здесь λ — дебаевская длина; cα0 — равновесная концентрация α-компоненты в растворе;
C = λ
r ^
ss o R
1/2
Так, если температура T
F 2Vz2c
F ^ z a c a 0
V a J
меняется от 283 до 353 К (10–80 °С), то величина X меняется примерно на 10 % .
Подвижность ионов
Подвижность ионов обычно определяют из соотношения Нернста—Эйнштейна [ 1, с. 258 ]
D a = R TU a ,
где u α — подвижность α -го иона. Отсюда, используя (27), легко можно найти характер температурной зависимости для подвижности
u
α
D α
R T
C α exp
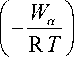
R T
ВЫВОДЫ
В работе приведены условия правомерности замыкания системы зависящих от времени уравнений массопереноса в растворе электролита электростатическим уравнением. Показано, что этим уравнением должно быть уравнение Пуассона с соответствующими значениями плотности заряда в дискретные моменты времени. Отмечено, что его замена условием электронейтральности является некорректной. Приведены зависимости некоторых параметров массопереноса от температуры.
Список литературы О замыкании электростатическим уравнением системы зависящих от времени уравнений массопереноса вещества в электропроводящих жидких растворах
- Ньюмен Дж. Электрохимические системы. М.: Мир, 1977. 464 с.
- Князьков Н.Н., Шарфарец Б.П., Шарфарец Е.Б. Базовые выражения, используемые в электрокинетике. Обзор//Научное приборостроение. 2014. Т. 24, № 4. С. 13-21.
- Шарфарец Б.П., Шарфарец Е.Б. О выборе методов решения уравнения Пуассона в общем случае распределения объемной плотности заряда и о постановке краевых условий в электрокинетических задачах (обзор)//Научное приборостроение. 2015. Т. 25, № 1. С. 65-75.
- Стрэттон Дж.А. Теория электромагнетизма. М.: ОГИЗ, 1948. 539 с.
- Bruus H. Theoretical Microfluidics. Oxford University Press, 2008. 346 p.
- Manzanares J.A., Kontturi K. Diffusion and Migration//Encyclopedia of Electrochemistry. Wiley-VCH., 2007. P. 81-121.
- Физическая энциклопедия. Т. 1. М.: Советская энциклопедия, 1988. 699 с.
- Википедия. Коэффициент диффузии. URL: (https://ru.wikipedia.org/wiki/Коэффициент_диффузии).


