О зависимости активационного объема при возврате в сплаве АМГБ от напряжения

В работе [1] была развита на основе концепции Кульман - Коттрелла - Эйтекина теория возврата механических свойств деформированных алюминий-магниевых сплавов при длительной изотермической выдержке. В итоге для скорости возврата было получено уравнение

^ = -Х(ст-а°)2ехр ат '       '

и_о-У*<д-а°₆) \ (1)

RT j

выражение (4) действительно хорошо описывает экспериментальную зависимость У* от ст при ст >300 МПа (линии 1). Можно добиться (несколько худшего) согласия и в более широкой области ст > 250 МПа, если принять значения И_о=22О см³/моль и a =24,5-Ю³ Дж/моль (линии 2 на рисунке). Предел текучести ненаклёпанного сплава ст® принимался равным 165 МПа.

где о - внутреннее напряжение (предел текучести), т - время, Стд - исходный (сразу после наклёпа) предел текучести, U_o - энергия активации, К* - активационный объём, R - газовая постоянная, Т - абсолютная температура, а X - константа. При интегрировании выражения (1) в [1] предполагалось, что активационный объём У* от напряжения о не зависит, и в результате было получено следующее уравнение возврата:

Если подставить (4) в дифференциальное уравнение возврата (1), последнее примет вид

da t/т

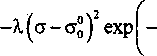
Це-УоЛо-д^-а

RT

аналогичный (1). Поэтому и решение уравнения (5) будет аналогично выражениям (2) и (3):

ст = ст0

RT ст0-ст”

0 ”

RT      f C7o-a-^_o-CT")

ХЕ₀(ст₀-ст«)²              RT

где характеристическое время процесса т ^                         <3>

⁰ ХК*(о₀-ст“)^{2 Р}( RT )

Заметим, что в тексте статьи [1] в формулах (1) и (2) были допущены опечатки, исправленные здесь.

Между тем анализ экспериментальных результатов по возврату в деформированном сплаве АМгб при различных исходных уровнях упрочнения показал, что объём У* имеет отчётливую зависимость от внутреннего напряжения (исходного предела текучести д^, которая показана на рисунке и которую можно попытаться учесть в теории возврата, если допустить, что изменение внутрен него напряжения а в ходе возврата влияет на величину У* так же, как предел текучести о0 после начального деформационного упрочнения.

В уравнении (1) произведение K* (o-aJ) вычитается из постоянной величины U_Q, поэтому удобнее всего искать аналитическое выражение зависимости У* от ст в виде

^ = ^+-^" W

СТ ст0

На рисунке показано, что при У_о = 252 см³/моль и а = 17,4-10³ МПа-см³/моль [Дж/моль]

С формальной точки зрения отличие уточнённой теории заключается в снижении «энергии активации» с С/о=126,О до UQ - а = 126,0-17,4=

=108,6 кДж/моль и «активационного объёма» с У* = 325,2 до Ко = 252 см3/моль, что приводит к увеличению характеристического времени т0 с 2,87 до 3,42 ч (при ао = 400 МПа и 7=295 К; для X принято значение 0,0286 (Па-ч)~’, как в [1]).

Уравнение (4) хотя и очень удобно для анализа, но описывает опытную зависимость И* от ст лишь в ограниченной области значений. Более точное выражение можно получить, если представить произведение У*-(<з-а⁰₀) в виде квадратичной параболы:

К*7ст-Сто) = ао+aj 7ст-сто) или

(     о)2

а0+а, (ст-сто

СТ-СТо

-^_+а1.(ст-ст°). (8) ст-ст₀ '       '

Кривые 3 на рисунке показывают, что при значениях коэффициентов ао=44,О-1О3 Дж/моль и aj =5,84-10~13 м3/(Па-моль) формула (8) действи тельно хорошо описывает экспериментальные результаты во всём исследованном интервале значений ст0. Её недостатком является то, что при

Работа поддержана РФФИ и Администрацией Челябинской области (грант 04-02-96006-р2004урал_а), а также грантом поддержки ведущих научных школ НШ-778.2003.3.

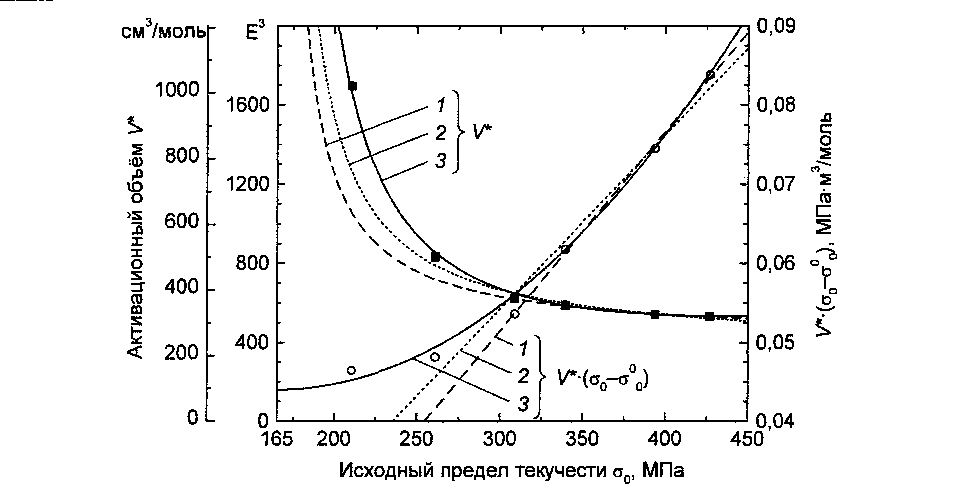
Зависимость активационного объёма процесса возврата V * от исходного предела текучести а₀ в сплаве АМгб. Точки - экспериментальные данные, приведённые в [1]; кривые 1 - расчёт по уравнению (4) при Gg = 165 МПа, И_о = 252 см³/моль и а = 17,4 кДж/моль; кривые 2 - то же при К_о = 220 см³/моль и а = 24,5 кДж/моль; кривые 3 - расчёт по уравнению (8) при а =44,0 кДж/моль и а_} = 5,84-Ю^-13 м³/(Па-моль)

(а-По)>274 МПа, то есть а >439 МПа, убывание Г* сменяется возрастанием, но к ошибке это не приведёт, поскольку такие уровни упрочнения на практике не встречаются.

Подставим (8) в дифференциальное уравнение возврата (1) и проинтегрируем его:

ехр -х   <    1     3    15     )

erfx = l--Д—Ц 1—^-+-4—^+... . (11)

du-x  V   lx¹  4х⁴  8х°    )

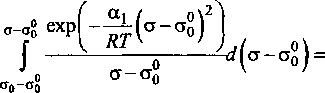
Ошибка этого разложения не превышает первого отброшенного члена [2, с. 71]; если ограничиться двумя первыми слагаемыми в скобках, то относительная погрешность результата будет менее 0,05 при х> 1,038, что соответствует

а > 232 МПа. В итоге после сокращения подобных

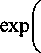
^о-ао

RT

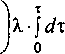
слагаемых уравнение (10) преобразуется к виду

Интеграл в левой части легко берётся по частям, если вспомнить, что dx/x² = -d^jx)^:

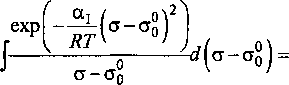
2ajX RT

ехр —----- -т.

I RT )

Введя, по аналогии с [1], переменную

(Ю)

где

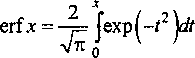
- интеграл вероятно

сти, для которого справедливо разложение

z =———_; выражение (12) можно переписать в

0 ~СТ0

более компактном виде:

-1- ехр ^(oa-a“)2(2z-z2) =- + 1 ,(13) где характеристическое время (сравни (3) и (7)) т„ =-----(а. - о") ехр —5---5---1^-2---. (14)

° 2а,Х ⁰   °                 RT )

Прологарифмируем (13):

-3ta(l-z) + ^(Q0-o°)2(2z-z2) = taP + ^^^

Мирзаев Д.А., Окишев К.Ю.

На сравнительно ранних стадиях возврата, когда z «1, можно удержать в левой части два члена разложения логарифма в ряд Тейлора: -ln(l-z)»z + z72= и тогда (15) преобразуется в квадратное уравнение относительно z. Поскольку z не может быть больше единицы, это уравнение имеет единственный корень

откуда и были найдены значения V*, использованные выше для нахождения параметров уравнений (4) и (8). Однако если V* меняется в ходе возврата согласно этим уравнениям, то наклон кривых ст(1пт) должен быть несколько иным. Даже при использовании уравнения (2) с постоянным активационным объёмом

2£ + 3- (2£ + 3)2-2(2£-3)-1п —+1

V ____________________ У^то Л (16)

da

<71пт

у*

RT а₀-а”

2^-3

где через £ обозначена безразмерная величина а‘ (ст -а0)2- Окончательное выражение для предела текучести спустя время т будет выглядеть следующим образом:

а если V* описывается уравнениями (4) и (8), то, согласно (6) и (19),

da

1 2

гЛпт         ст0-Оо

ст

Сто-Сто х

2£ + 3- (2£ + 3)2 -2(2£-3)-Ь —+1

V                          \то .

X-------------------------------------

2^-3

• (17)

Согласно (14), характеристическое время здесь

т0 =-----------т- • ехр

0 2Ща0-а“) F

RT

• (18)

Уравнение (17) довольно сложно, однако при не слишком больших временах т можно воспользоваться формулой Vl-x «1-х/2, и тогда (17) примет вид, похожий на (2) и (6):

о    /      \

CT = gg-a°~g° -ln|— + 1 ■

25 + 3   Uo  J

Сделаем численную оценку т₀. Коэффициенты Оо и ai равны о₀=44,0-10³ Дж/моль и О] = 5,84-10~¹³ м³/(Па моль). Остальные величины для сплава АМгб были определены в статье [1]: ст° = 165 МПа, U_o = 126-10³ Дж/моль, X =0,0286 (Па-ч)"¹. Тогда при Т = 295 К и с₀ = 400 МПа величина £ = 13,1, а т₀=3,65 ч. Как упоминалось выше, расчёт по формуле (3) при постоянном активационном объёме К* = 325,2 см³/моль даёт т₀ = 2,87 ч, а по формуле (7) при у_о =252 см³/моль и a = 17,4-10³ Дж/моль - т₀ = 3,42 ч.

Однако прежде чем пользоваться выражениями (2), (6) и (19) для прогнозирования изменения предела текучести при возврате, необходимо вспомнить, что значения активационного объёма V* не измеряются непосредственно - они рассчитывались на основании наклона экспериментальных зависимостей ст от 1пт. По теории Кульман -Коттрелла - Эйтекина

da __fK^T'

1пт~

и

da

Лит

2о, о 3

RT g₀-

соответственно. Зная наклон кривых для ряда исходных уровней упрочнения ст₀, можно рассчитать величину V* либо параметры И_о или о_ь В таблице приведены результаты такого расчёта, основанного на экспериментальных данных [1] о возврате в сплаве АМгб при Т= 295 К. Видно, что эти константы значительно изменяются с изменением ст₀. Это говорит о том, что уравнения (4) и (8) неверно описывают зависимость активационного объёма при возврате от напряжения.

Можно попытаться построить и ещё один вариант теории возврата, приняв во внимание возможность обратных переходов атомов около точек закрепления дислокаций. В этом случае вместо (1) нужно будет записать

da dx

где

ет

= -К

K*-(ct-Go)

ехр +---1---—

RT

= Ksh

-ехр

КГ

TZ sh /        0 \

(ст-СТо)

RT

К = 2С ехр (- U_o /КГ) ■ Функция sh обеспечива-

обращение скорости возврата в

ст_>ст”. Решение дифференциального (24) имеет вид

th(x/2) th(x₀/2)"

К*-(ст-ст°) где х =-----------, а хп =

RT

у* -К —т

RT -

Оо ~сто

RT

ноль при уравнения

Если использовать найденные ранее значения Сто и К*, то при о = 400 МПа и Т =295 К получим х = 31,2. При таком значении х, и даже вдесятеро меньших, sh х « е"^х /2, то есть модель фактически переходит в исходную.

Таблица

Параметры уравнений, описывающих активационный объём, рассчитанные по наклону экспериментальных кривых возврата при 295 К (т выражено в сутках)

Оо	°0 ~ст0	do	V* по (20)	V* по (21)	Ко по (22)	aj по (23)
		tZInT
МПа (по [1])			см3/моль			см3/(МПа-моль)
427	262	7,67	320	301	301	0,557
394	229	7,53	326	304	304	0,641
339,5	174,5	6,92	354	326	326	0,895
309	144	6,57	373	339	339	1,119
261	96	4,89	502	451	451	2,213
210,5	45,5	2,40	1022	914	914	9,453

Иначе говоря, теория возврата, в которой учитывается возможность изменения активационного объёма в процессе снижения внутреннего напряжения, приводит к непреодолимому расхождению теоретических расчётов и эксперимента. В работе [1] были рассмотрены две модели возврата, позволяющие объяснить экспериментальные закономерности: а) движение и аннигиляция винтовых дислокаций со ступеньками и б) выход дислокаций из субзёренных границ. И в том, и в другом случае V* ~ ЬЧ, где 1 - расстояние между ступеньками на винтовых дислокациях или между узлами дислокационной сетки. Уменьшение V* по мере роста Сто обусловлено увеличением числа пересечений по мере возрастания степени пластической деформации. Однако мы полагали, что из-за скольжения ступенек вдоль линии дислокации и аннигиляции расстояние 1 возрастает со временем, вызывая возрастание активационного объёма. Но возможно, что миграция ступенек затруднена атомами магния, и поэтому активационный объём остаётся неизменным в ходе возврата. Изменить его можно путём увеличения числа пересечений дислокаций.

Таким образом, результаты данного исследования свидетельствуют о постоянстве активационного объёма V* в ходе возврата, хотя на величину

V* и влияет уровень предела текучести после исходной нагартовки.

Выводы

Сделана попытка учесть возможность изменения активационного объёма в ходе возврата в сплаве АМгб в рамках модифицированной теории Кульман - Коттрелла - Эйтекина. На основании имеющихся опытных данных было использовано несколько вариантов описания такой зависимости. Во всех случаях наблюдалось резкое расхождение результатов расчёта с экспериментом, что, по-видимому, свидетельствует о том, что величина активационного объёма остаётся постоянной в процессе возврата, хотя и зависит от степени исходной нагартовки.