Об адекватности имитационной модели функционирования системы переработки диоксида углерода обитаемых космических объектов

Проектирование и наземная экспериментальная отработка — важнейшие этапы создания систем пилотируемого космического аппарата (ПКА), так как последующие летные испытания, совмещенные со штатной эксплуатацией, не позволяют использовать их результаты для устранения последствий конструкторских решений ошибочного характера. На этапе проектирования перспективных систем ПКА необходимо решать задачи, связанные не только со свойствами их составных частей (элементов и подсистем), но также и с закономерностями функционирования системы в целом. Следствием этого является необходимость решения широкого круга специфических задач, к которым относятся: определение общей структуры системы и требований к элементам и подсистемам, организация взаимодействия между ними, выбор оптимальных режимов функционирования, оптимальное управление протекающими в системе процессами, учет влияния внешней среды и т. п. [1].

Решение этих задач на этапе эскизного проектирования может проводиться методом математического моделирования с применением аналитических и имитационных методов. Результаты моделирования позволяют определить значения показателей эффективности системы, обосновать ее оптимальную структуру, выявить закономерности протекающих в ней процессов, учесть влияния внешней среды и т. п. Математическое моделирование является мощным и эффективным инструментом исследования сложных объектов, систем и процессов в различных областях [1]. В связи с этим важной задачей в совершенствовании процесса разработки систем ПКА является разработка имитационной модели, наиболее точно описывающей функционирование системы-оригинала. Проведение вычислительных экспериментов с использованием имитационной модели функционирования вновь разрабатываемой системы на стадии проектирования позволит не только описать функционирование отдельной системы на уровне реализуемых процессов, но и рассмотреть возможные алгоритмы оценки и анализа показателей назначения и прогнозирования функционирования разрабатываемой системы на всех этапах ее жизненного цикла.

В настоящее время РКК «Энергия» и НИИхимммаш разрабатывают систему переработки диоксида углерода (СПДУ), входящую в состав интегрированной регенерационной системы обеспечения газового состава ПКА для длительных автономных космических полетов. Система предназначена для удаления из газовой среды обитаемого модуля диоксида углерода, его концентрирования до 99% и последующей переработки по реакции гидрирования до газообразных веществ: метана и паров воды [2]. Разработана имитационная модель функционирования СПДУ, которая позволяет не только получать подробную статистику о различных аспектах функционирования системы в зависимости от входных параметров, но и дает возможность проводить анализ технических требований и оценку показателей назначения системы.

В ходе имитационного моделирования были определены наиболее значимые факторы (входные параметры модели), варьирование которых приводит к изменению основного показателя назначения — «выход по воде». По результатам моделирования выбраны конструктивные параметры внешней теплоизоляции, геометрические размеры реакционной зоны и рекуператора, а также определены оптимальные значения входных параметров блока гидрирования диоксида углерода [3]. Однако для использования результатов вычислительных экспериментов на последующих этапах разработки системы необходимо проверить имитационную модель функционирования СПДУ на адекватность.

Обоснование критерия адекватности имитационной модели функционирования СПДУ

Для проверки адекватности имитационной модели необходимо сравнить результаты вычислительных экспериментов с данными, полученными при испытаниях конструкторско-технологического макета или опытного образца СПДУ. Как уже говорилось, основным показателем, определяющим соответствие СПДУ своему функциональному назначению, является «выход по воде». Значения этого параметра и необходимо сравнивать.

Критерии проверки гипотез об однородности выборок разных серий измерений представляют собой задачи статистического анализа [4]. При статистическом анализе результатов экспериментов применяют критерии проверки гипотез об однородности математических ожиданий (об однородности средних) [5].

В общем случае проверяемая гипотеза о равенстве математических ожиданий µ, соответствующих k выборкам, имеет вид H ₀ : µ₁ = µ₂ = ... µ _k при конкурирующей гипотезе H ₁ : µ _{i 1} ≠ µ _{i 2} хотя бы для некоторой пары индексов i 1, i 2.

Для проверки гипотезы H ₀ может использоваться ряд параметрических критериев:

• •    сравнения двух выборочных средних при известных дисперсиях;

• •    сравнения двух выборочных средних

при неизвестных, но равных дисперсиях (критерий Стьюдента);

• •    сравнения двух выборочных средних при неизвестных и неравных дисперсиях.

Одним из основных предположений при построении параметрических критериев является принадлежность наблюдаемых случайных величин нормальному закону распределения [5]. При проведении вычислительных экспериментов с использованием имитационной модели и при испытаниях конструкторско-технологического макета проводилась проверка нормальности выборок. Далее необходимо проводить сравнение средних значений выборок, предварительно проанализировав связь их дисперсий.

Для подтверждения адекватности имитационной модели воспользуемся t -критерием Стьюдента сравнения двух выборочных средних при неизвестных, но равных дисперсиях. Статистика критерия определяется формулой [5, 6]:

t = m - n m + n

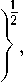
где s =

Здесь

( n - 1) s 2 + ( m - 1) s 2 n + m – 2

⁵ 2 =

n

-—T£(x - -)2; n - 1;“^  !

m

s2’ = ^—T К y - y)2; (3) 2 M 1 i = 1

^–x , y ^– , s ² ₁ , s ₂ ² — выборочные оценки средних и дисперсий соответствующих выборок; m , n — количество измерений в выборках.

Перед сравнением двух выборочных средних все-таки необходимо убедиться в статистической неразличимости выборочных оценок дисперсий разных серий измерений. Для проверки гипотез об однородности дисперсий выборок будем применять критерий Фишера, так как он является более распространенным для сравнения двух выборок нормально распределенных случайных величин, и его статистика имеет простой вид [4, 6, 7]:

s ²

F = ¹ . (4) ^s 2 ²

При расчете F -параметра в числителе стоит большая величина. Число степеней свободы ν — это разность между числом экспериментов и числом значений независимых случайных величин, полученных в результате этих экспериментов, которые не позволяют оцениваемой в результате этих экспериментов величине (например, среднему значению) принимать какое-либо другое значение, отличное от полученного по окончании их проведения [7]. В большинстве случаев ν = n – 1, где n — количество измерений в выборке.

Найденное экспериментальное значение F -параметра, вычисленное по формуле (4), сравнивается с критическим значением F _кр , соответствующим максимальному значению отношения двух дисперсий, при котором еще можно считать гипотезу о равенстве рассматриваемых дисперсий справедливой.

F _кр по числу степеней свободы и заданному коэффициенту риска ( β = 1 – a , где a – доверительная вероятность) берется из таблиц [7]. Значение числа степеней свободы ν₁ дисперсии, стоящей в числителе выражения (4), определяет значение F _кр по столбцу, а значение ν₂ — по строке. Если F <  F _кр , то гипотеза о равенстве выборочных дисперсий справедлива. В противном случае рассматриваемые дисперсии относятся к различным генеральным совокупностям исследуемой величины.

Задача сравнения средних двух нормально распределенных совокупностей при неизвестных и неравных (по выборочным оценкам) дисперсий известна как проблема Беренса–Фишера [6] по имени авторов, впервые ее сформулировавших. Для решения этой задачи на практике обычно используются различные приближения [6], например, критерии Корхана– Кокса, Сатервайта, Уэлча и т. д. Статистика этих критериев имеет следующий вид [6]:

t = У(Х~У ^ (5)

s1       s2

где s ² = n + m , а s ² ₁ и s ₂ ² вычисляются по

формулам (2) и (3).

Критическими значениями этих критериев являются квантили распределения Стьюдента, и отличаются они лишь числом степеней свободы. Для решения

задачи сравнения средних двух нормально распределенных совокупностей при неизвестных и неравных (по выборочным оценкам) дисперсий чаще всего используют критерий Сатервайта, так как с ростом числа степеней свободы погрешность вычислений с использованием критерия Сатервайта не превышает 0,001. Число степеней свободы критерия Сатервайта определяется по формуле [6]:

ν c

n – 1

s 1

n

+

т - 1

s2

т ,

–1

Таким образом, если после сравнения двух выборочных оценок дисперсий с использованием критерия Фишера подтверждается их статистическая неразличимость, то для сравнения двух выборочных средних воспользуемся t -критерием Стьюдента (1). Если же после сравнения двух выборочных оценок дисперсий не подтверждается их статистическая неразличимость, то для сравнения двух выборочных средних воспользуемся критерием Сатервайта (5).

Для упрощения реализации вычислений в программном обеспечении вместо использования громоздких таблиц квантилей распределения Стьюдента воспользуемся аппроксимацией [6]:

t _α ( ν ) = u _α

1 –

u ² _α + 1 ^–1 4 ν

где u _a — a -квантиль стандартного нормального распределения случайной величины с доверительной вероятностью a = 0,95 (определяется вероятностью безотказной работы СПДУ).

Для нахождения u _a используем аппроксимацию [6]

u _α = 2,0637 ln

1 – α

0,4271

0,16

1,5774, (7)

абсолютная погрешность которой меньше или равна 0,0008 для оценки дисперсий при доверительной вероятности 0,5 ≤ a ≤ 0,999.

Проводим вычисления по формулам (1) и (6) или (5) и (6). Если | t | <  t _a ( ν ), то нулевая гипотеза равенства средних не отклоняется. Следовательно, имитационная модель функционирования СПДУ адекватна. В случае отклонения нулевой гипотезы имитационная модель неадекватна и требует доработки.

Результаты проверки имитационной модели на адекватность

Для примера была взята выборка значений целевого параметра («выход по воде») за один случайно взятый день проведения испытаний (колонка Х таблицы). Условия проведения испытаний были воспроизведены на модели, и получены соответствующие результаты моделирования (колонка Y таблицы). Проведем анализ адекватности модели.

Выборки значений результатов измерений

№ наблюдения	X	Y	( xi – x – )2	( yi – y – )2
1	61,15	59,91434	0,166736	0,366878
2	60,58	60,37935	0,026136	0,019795
3	60,77	59,93299	0,000803	0,344633
4	60,62	61,29437	0,014803	0,59958
5	60,90	60,93429	0,025069	0,1716
6	60,04	60,58097	0,492336	0,003712
7	60,64	60,00318	0,010336	0,267149
8	60,49	60,34766	0,063336	0,029716
9	60,44	61,18592	0,091003	0,443391
10	61,08	60,39066	0,114469	0,01674
11	60,92	60,41018	0,031803	0,01207
12	61,27	60,86662	0,279136	0,120115
Сумма	728,9	726,2405	—	—
Среднее	60,74657	60,52	—	—

Выполним проверку нормальности распределений значений из выбранных последовательностей наблюдений, используя W -тест Шапиро–Уилка [6], как имеющий наибольшую мощность для выборок с небольшим количеством наблюдений (рис. 1, 2).

Проверка гипотезы H0 теста Шапиро– Уилка заключается в том, что случайная величина, выборка X которой известна, распределена по нормальному закону. Альтернативная гипотеза Н1 заключается в том, что закон распределения не является нормальным. В обоих случаях wфакт > wкр [3], следовательно, не опровергается гипотеза, что наблюдаемые распределения результатов и модельного, и натурного экспериментов не отличаются значительно от теоретически ожидаемого нормального распределения.

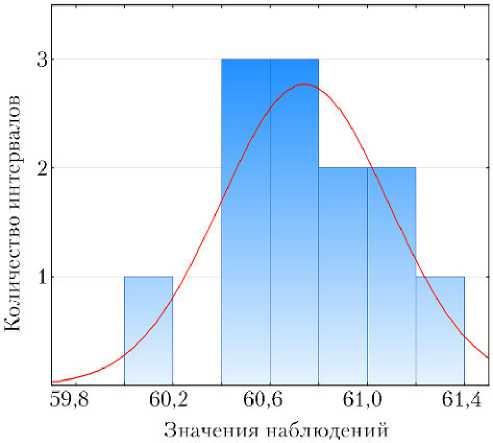
Рис. 1. Выборка натурных наблюдений, W-тест Шапиро– Уилка, w = 0,973

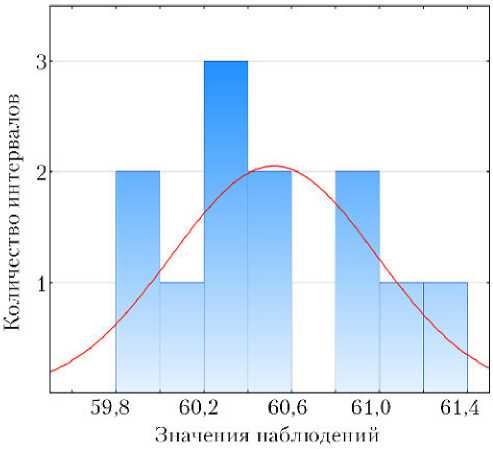
Рис. 2. Выборка наблюдений на модели, W-тест Шапиро– Уилка, w = 0,929

Для проверки гипотез об однородности дисперсий двух серий измерений с использованием критерия Фишера (4) проведены расчеты:

1 3159

F = 12 ,, 33 19 55 94 = 0,5493.

Для двух выборок, содержащих по 12 наблюдений, и уровня значимости 0,05 F _кр = 2,82. Полученное значение F меньше критического, следовательно, можно считать гипотезу о равенстве рассматриваемых дисперсий справедливой. Таким образом, для подтверждения адекватности имитационной модели воспользуемся t -критерием Стьюдента сравнения двух выборочных средних при неизвестных, но равных дисперсиях.

По выражению (2) находим выборочную оценку среднеквадратичного отклонения первой серии измерений:

s ₁ ² = 1,3159.

По выражению (3) находим выборочную оценку среднеквадратичного отклонения второй серии измерений:

s ₂ ² = 2,3954;

s ² =

( n – 1 ) s ₁² + ( m – 1) s ₂ ²

_{n + m – 2}

(12 –1) 1,3159 + (12 – 1)2,3954

12 + 12 – 2           ^{= 1,8557.}

Для выборок, содержащих одинаковое количество наблюдений, статистика критерия Стьюдента (1) принимает следующий вид [6]:

t =

x – y

= 2,02.

Для доверительной вероятности a = 0,95 и степени свободы v = n + m = 12 + 12 - 2 = 22 по аппроксимациям (6) и (7) вычисляем t _a ( v ) = 2,074. Так как 1 1 1 <  t a ( v ), то нулевая гипотеза равенства средних разных серий измерений не отклоняется, что подтверждает адекватность модели.

Выводы

Подтверждено предположение о том, что выборочные оценки дисперсий разных серий измерений, полученных в результате вычислительных экспериментов с использованием имитационной модели и при испытаниях конструкторско-технологического макета, не имеют значимых различий.

Путем сравнения равенства средних двух серий измерений с применением t -критерия Стьюдента подтверждена адекватность имитационной модели функционирования СПДУ.

Результаты имитационного моделирования, такие как конструктивные параметры внешней теплоизоляции, геометрические размеры реакционной зоны и рекуператора, оптимальные значения входных параметров блока гидрирования диоксида углерода, можно использовать на последующих этапах разработки системы.