Об алгоритме построения тёплицевых матриц с заданным числом компонент связности дополнения предельного спектра

Введение. В данной работе решается задача экспериментальной проверки оценок снизу максимального числа компонент связности дополнения предельного спектра ленточных тёплицевых матриц, символы которых — лорановские полиномы заданной степени. Вычисляются значения параметров символа последовательности ленточных тёплицевых матриц, дополнение предельного спектра которых имеет заданное число компонент связности из промежутка значений, границы которого найдены в работе [1]. Заметим, что это — часть общей задачи исследования геометрии предельного спектра ленточных тёплицевых матриц [2–6]. Отметим, что в случае тёплицевых матриц с более сложным символом предельный спектр часто допускает явное и относительно простое описание по сравнению с предельным спектром ленточных тёплицевых матриц [7–8]. Уточним постановку задачи и напомним необходимые для понимания

^∗ Работа выполнена в рамках инициативной НИР.

^∗∗∗ The research is done within the frame of the independent R&D.

работы понятия [5, 9]. Пусть f — комплекснозначная функция, аналитическая в окрестности окружности единичного радиуса S ¹ = { z е C: |z | = 1 } :

f ( ^z ) = Z akz^k . k е Z

то есть матрицу T (f )=(a, ,)n   , матричные эле- n             i, j н, j=1

Будем обозначать через Tn (f) тёплицеву матрицу размера n х n, менты которой задаются формулой ai j = aij , где ak находятся из (1). Отметим, что у тёплицевой матрицы на каждой из диагоналей, параллельных главной, стоят одинаковые элементы. Заметим, что если для k < -r и для k > h , ak = 0, h то есть аналитическая функция f (z) превращается в лорановский полином f (z)= Z akzk , то соответствующая та-k=-r кой функции тёплицева матрица называется ленточной.

■_{n + 1} матрицы T n ^{( f} ) ^так, ^{что Л} n , / |<|^Л n j при

Упорядочим каким-нибудь образом собственные значения i < j. Множество предельных точек последовательностей {лn i }nбудем называть предельным спектром последовательности тёплицевых матриц {Tn (f)}“= 1 и обозначать через оl (f).

Далее выясним, как связан предельный спектр с функцией f (z) (которую также называют символом каждой из матриц последовательности {Tn (f)}”= 1) и какова геометрическая структура предельного спектра. Для самосопряжённых матриц ответ известен давно. Предельный спектр — это отрезок вещественной прямой. Несамосопряжённый случай намного сложнее. В работе Ф. Спитцера и П. Шмидта [2] было получено описание предельного спектра несамосопряжённых тёплицевых матриц в терминах совпадения модулей корней многочлена строящегося по символу последовательности ленточных теплицевых матриц. Используя такое описание, Ф. Спитцер и П. Шмидт доказали, что предельный спектр является либо одномерным множеством, являющимся объединением аналитических дуг, либо нуль-мерным множеством, состоящим из точки. Позднее Ульман доказал связность предельного спектра [3]. Более тонкие геометрические вопросы о строении предельного спектра ленточных несамосопряжённых матриц являются открытыми вопросами до настоящего времени. В данной работе исследуется вопрос о числе компонент дополнения предельного спектра ленточных тёплицевых матриц. Экспериментально доказывается, что число этих компонент может быть сколь угодно большим. Построены конкретные примеры символов — полиномов Лорана, таких, что предельный спектр соответствующих им тёплицевых матриц разбивает комплексную плоскость на максимальное число компонент связности, равное

k + 1

, где 2 k — степень полинома Лорана, являющегося символом данной последо-

вательности тёплицевых матриц. В основе работы лежит способ специального выбора параметров полиномов Лорана, являющихся символами тёплицевых матриц, предельный спектр которых разбивает комплексную плоскость на задан-

ное число компонент связности r , где 1 <  r <

k + 1

. Таким образом, на основе численного эксперимента получаем

некоторые оценки снизу для максимального числа компонент, на которые может разбивать комплексную плоскость предельный спектр последовательности тёплицевых матриц с символом заданной степени k . Заметим, что в данной работе уточняется часть результатов, анонсированных в работе [10]. Следует также отметить, что вопросы геометрии предельного спектра играют большую роль при изучении асимптотики собственных чисел тёплицевых матриц больших размеров [4]. В работе использованы следующие стандартные обозначения: о ( A ) — спектр оператора A : о (А) = { Л е C: A -U - необратим } .

Основной результат работы. Рассмотрим многочлен

b(t) = ц + t ^{- k} ( t -a ) ^k ( t -p ) k ,                                                (2)

где ц,а,в  являются комплексными числами, и a-p*0. Пусть a(t) = t-1(t-a)(t-p). Легко видеть, что b (t) = ц + (a (t))k.

Далее численно проверим следующий результат, анонсированный в [4].

Теорема 1. Если k = 1 или k = 2, тогда C \ о l ( b ) связен.

Информатика, вычислительная техника и управление

• 2.    Если k >  3 тогда C \ о l ( b ) имеет по меньшей мере

  k + 1

  
  
3. Для каждого натурального числа j между 1 и

компонент (включая неограниченную компоненту).

k + 1

существуют такие а , в , что C \ а l ( b ) имеет ровно j компо

нент. Именно а , р находятся из уравнений

- ^(а + р ) + 2 д/ ^а-р — f 1 , ^{-(а +} Р^{)- 2} 4 ^а'р ^— f 2 .

При этом f 1 , f 2 следует выбирать так, чтобы разность значений их аргументов удовлетворяла следующему условию:

n (r - 1 )                      n Г

---:---<\arg^(f । ) ^- arg^(f2)\ < —, r — 1 ,...k . kk

В этом случае число компонент связности дополнения предельного спектра будет равно

r + 1

Замечание. Приведём явный способ построения символа тёплицевых матриц, предельный спектр которых делит комплексную плоскость на число s — 1,...,k компонент связности, уточняющий приведённую выше теорему. Зафиксируем произвольное комплексное число z 0 , отличное от 0. Выберем угол ф , удовлетворяющий следующему условию:

п ( s - 1) k

n s

<ф<   .

k

Положим f — z о , f 2 — e i ^ф z 0 . Мы можем, используя формулы (3) явно найти значения параметров а , в , чтобы выполнялось условие (4):

i ф а—-+ 2 z о e .

в — - z^yz- - 2 z o e '

Примеры вычисления предельных спектров. Ниже, используя описанную выше схему вычисления параметров символа тёплицевой матрицы, предельный спектр которой разбивает комплексную плоскость на заданное число r компонент связности, находим значения параметров символа. Результаты вычислений сведены в таблицу.

Отметим, что значение ц выбирается так, чтобы |ц - ( а + в ) >  0 и было достаточно мало, а | а - в| >  0 достаточно вели

ко. Будем рассматривать символ b ( t ) — ц + t ^k ( t - а ) ( t -в ) с параметрами из следующей таблицы:

Связь числа компонент связности и параметров символа

Таблица 1

Число компонент r	Угол ф n (s -1 )      n s —--- <ф< — kk	f 1	f 2	а	в	ц	k
1	0 < ф < n , пусть ф— 1,11	8–7 i	9,8272+ 4,0529 i	0,7871– 0,1301 i	–9,7007+ 1,6036 i	–8,9+1,5 i	1
2	2 n — < ф< n, 3, пусть ф — 2,48	8–7 i	–2,0115+ 10,4381 i	3,1123+ 1,7868 i	–6,1065– 3,5058 i	2,7+1,7 i	3
3	4 n — < ф< n , 5, пусть ф — 2,52	8–7 i	–2,4273+ 10,3493 i	3,1624+ 1,9007 i	–5,9487– 3,5753 i	–2,5–1,5 i	5
4	6 n —<ф<п , 7, пусть ф — 2,71	8–7 i	–4,3382+ 9,7046 i	3,3599+ 2,4816 i	–5,1908– 3,8340 i	–1,8–1,3 i	7

Приведём примеры предельных спектров последовательностей тёплицевых матриц с символами вида (2), параметры которого заданы в таблице 1. Номера рисунков соответствуют номерам параметров символа из таблицы.

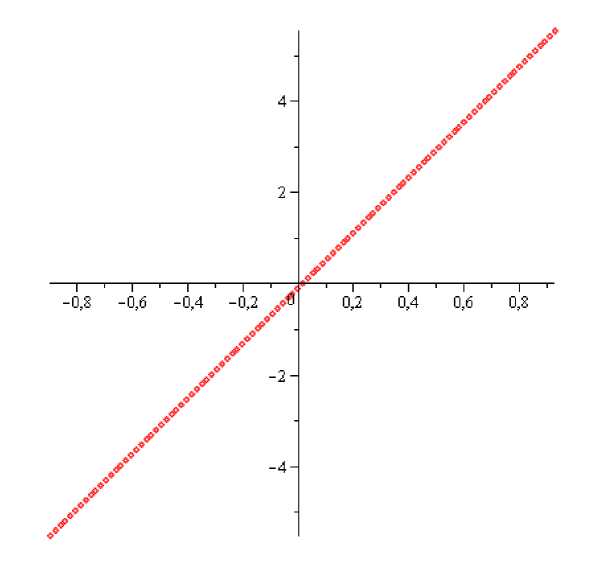
Рис. 1. Одна компонента связности дополнения предельного спектра

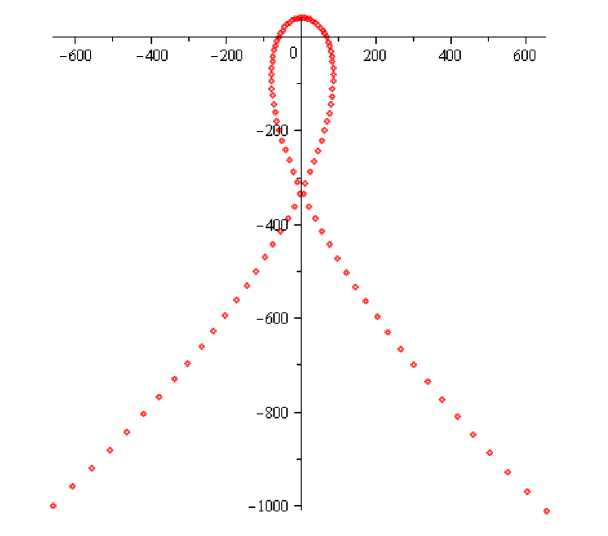
Рис. 2. Две компоненты связности дополнения предельного спектра

Информатика, вычислительная техника и управление

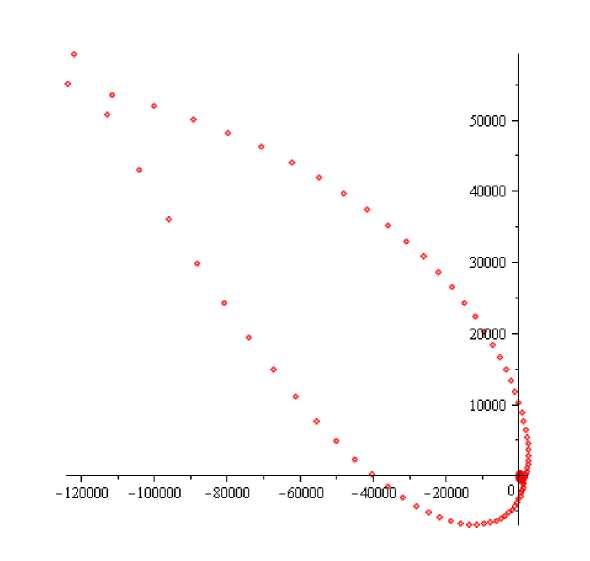
Рис. 3. Три компоненты связности дополнения предельного спектра

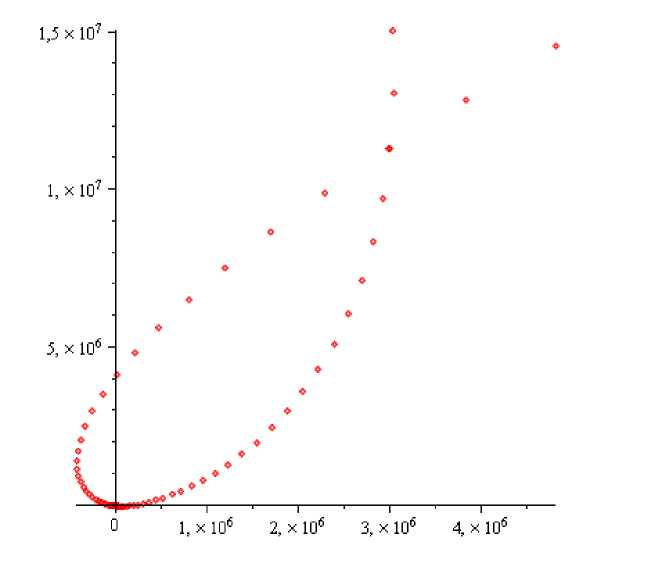
Рис. 4. Четыре компоненты связности дополнения предельного спектра

Замечание. К сожалению, возможности программы Maple аналитических вычислений не позволяют хорошо рассмотреть на рис. 4 число компонент связности дополнения предельного спектра из-за большой разницы масштабов различных компонент связности дополнения предельного спектра.

Сравнение предельного спектра и спектра ленточных тёплицевых матриц . Рассмотрим примеры вычисления спектра ленточных тёплицевых матриц достаточно больших размеров с рассмотренными выше символами. Такие спектры должны быть хорошими приближениями предельных спектров, построенных в предыдущем пункте. В настоящей работе важно показать, что в пределе по размеру матрицы спектры рассмотренных матриц стремятся к кривой, дополнение которой содержит нужное число компонент связности, такое же как и на соответствующих графиках из предыдущего пункта.

Рассмотрим тёплицевы матрицы с символом b(t) = ц +t-k (t - a) (t - p)k при k = 3, a = 3,1123 + 1,7868i, p = -6,1065 - 3,5058г, ц = 2,7 + 1,7i. (6)

В этом случае символ имеет следующий вид:

b ( t ) = t ³ + ( 8 , 9820 + 5 , 1570 i ) t ² + ( - 20 , 1961 - 34 , 5865 i ) t - 0 , 8233 - 480 , 6002 i +

.

+

t t3

t ²

- 497 , 4325 + 881 ,4213i

- 5687 , 1709 + 3376 , 5336 i 16135 , 0717 - 236 ,3335i

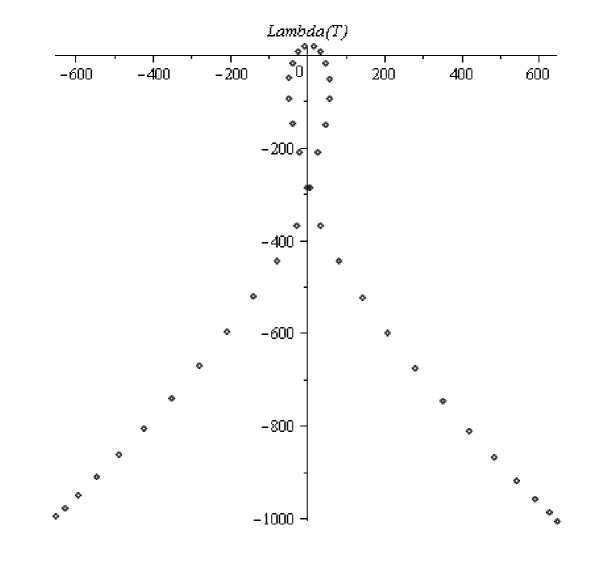
Рис. 5. График собственных значений тёплицевой матрицы с символом (7) размера n = 40

Заключение. Экспериментально исследован вопрос о числе компонент связности дополнения предельного спектра ленточных тёплицевых матриц, лорановский полином которых — многочлен вида b ( t ) = ц + t - k ( t - a ) k ( t - в ) k . Рассмотрен алгоритм построения тёплицевых матриц с данным символом и заранее заданным числом компонент связности дополнения предельного спектра. Экспериментально проверено, что для каждого натурального числа j между 1

и

можно подобрать такой символ b(t) = ц +t-k (t - a) (t - p)k, что предельный спектр тёплицевых матриц с к +1

этим символом делит комплексную плоскость ровно на j компонент связности. Этот результат даёт, в частности, оценку снизу для максимального числа компонент дополнения предельного спектра для ленточных тёплицевых матриц с символом — многочленом Лорана заданной степени.