Об амплитуде радиоотклика магнитосферы активной области на долгопериодные собственные колебания пятен

Using the example of simple modeling of the unipolar sunspot magnetosphere by the magnetic monopole, submerged in subpho-tospheric layers, and the temperature, varying with height as hyperbolic tangent, we show the following for cyclotron emission of microwave sources. Given insignificant changes in the intensity of the sunspot magnetic field, which result from oscillations of the sunspot as an entire structure, the amplitude of oscillations of I and V Stocks parameter brightness temperatures at a wavelength of 1.76 cm (NoRH) exceeds that of the magnetic field intensity oscillations by an order of magnitude in percentage terms. At a wavelength of 5.2 cm (SSRT), this amplitude is identical to that of the field oscillations.

В последние годы внимание исследователей привлечено к низкочастотным (с периодом около 1 ч) колебаниям пятен, физическое происхождение которых резко отличается от хорошо известных 3–5-минутных колебаний [1–4]. Если последние являются проявлением МГД-волн, захваченных и/или распространяющихся внутри магнитных силовых трубок пятна, то низкочастотные колебания связаны с квазипе-риодическими вертикально-радиальными смещениями всего пятна в целом как отчетливо локализованного и стабильного образования [3]. Такого рода колебания оказываются физически возможными в силу того, что солнечные пятна, по всей видимости, являются относительно мелкими, укорененными в неглубоких подфотосферных слоях образованиями: глубина так называемой нижней магнитной границы пятна, т. е. того подфотосферного уровня, ниже которого магнитное поле пятна резко уменьшается с глубиной, составляет всего три–четыре тысячи километров. Это теоретически предсказанное свойство солнечного пятна [5–7] уверенно подтверждается данными современной локальной гелиосейсмологии [8, 9].

Долгопериодные колебания пятен могут быть хорошо видны в радиодиапазоне на высотах, заведомо превышающих высоты образования спектральных линий, где такие колебания уверенно наблюдаются [1, 2]. Это связано с тем, что вертикальные смещения плазмы пятна, проявляющиеся в доплеровских сдвигах их спектральных линий, очень быстро убывают с высотой [1, 2], как это свойственно всяким гравитационным возмущениям. При этом изменения магнитного поля пятна, сопровождающие его вертикальные смещения, охватывают всю магнитосферу над пятном и проявляются на всех уровнях. Необходимо учесть, что мы рассматриваем очень медленные колебания пятна (период порядка часа). Альфвеновская скорость в короне над пятном составляет сотни и тысячи километров в секунду, так что перестройка магнитного поля над пятном происходит за секунды, т. е. практически мгновенно по сравнению с периодом медленных колебаний пятна как целого. Следовательно, по мере того как напряженность магнитного поля в пятне квазистатически изменяется вследствие его медленного колебания, в области над пятном изменяются и геометрическое положение, и физические параметры гирорезо-нансного слоя, излучающего в сантиметровом диапазоне. В соответствии с этим меняются квазипериодически и все характеристики радиоизлучения источника над пятном. По этой причине периоды собственных колебаний пятен как целого надежно и уверенно выявляются и в радиодиапазоне, в частности, на радиогелиографе Нобеяма [4].

В данной работе вычислена зависимость между изменениями магнитного поля на уровне фотосферы и изменениями яркостной температуры циклотронных радиоисточников над медленно колеблющимся пятном. Для моделирования изменений яркостной температуры во времени выбрана следующая модель униполярного пятна: магнитный монополь помещен под фотосферу на глубину h = 1.5 - 10 9 см, так что магнитное поле на его оси в центре пятна равно B 0 =3000 Гс (рис. 1).

Для описания распределения магнитного поля над пятном используется модель нескрученного магнитного монополя [9]:

d ² \-3/2

B ⁽ r , z ) = B 0 2 ( r ² ( z ⁺ d ) ⁺ 1 ) , ( z + d )

B r ( r , z ) = B z ( r , z ) r /( z + d ).

Здесь d – глубина погружения виртуального монополя, которая отсчитывается вниз от слоев пятна, видимых в белом свете; B ₀ – напряженность магнитного поля в пятне на его оси в центре на уровне этих слоев, т. е. на уровне вильсоновской депрессии. Имитация вертикальных осцилляций цилиндрического пятна определяется изменением B ₀ . Вычислим

И . А . Бакунина , A.A. Соловьев , Ю . А . Наговицын и др .

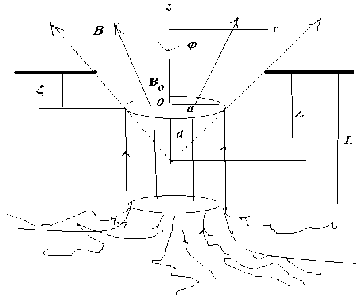
Рис . 1. Униполярное солнечное пятно . Используются ци линдрические координаты . ζ – глубина вильсоновской де прессии ; L – нижняя магнитная граница пятна , ниже которой магнитное поле резко убывает и становится размытым , « диффузным » в результате действия конвекции ; λ – глубина погружения виртуального монополя , которая описывает поле над пятном и отсчитывается от уровня фотосферы вниз ; d – глубина погружения виртуального монополя . Очевидно , что λ = ζ + d . Высота z отсчитывается вверх от пятна .

поведение яркостной температуры циклотронной эмиссии со 2-, 3-, 4-го гироуровней в случае наблюдения пятна, проходящего через центральный меридиан Солнца (ЦМ).

Распределение кинетической температуры верхней хромосферы — нижней короны задано в виде гиперболического тангенса:

7 — 7„

T (z) = To + A (th zo. + th z lz), делировании мы использовали следующую методику. Пятно покрывалось однородной сеткой (площадь, описанная вокруг круглого пятна, разбивалась на 69 равных маленьких квадратов) для данного θ (в нашем случае θ = 0 – ПЦМ). Из каждого узла сетки выпускался луч зрения, затем проводились вычисления, описанные выше, для всех точек (xk, yk). После этого выбирались точки, в которых максимальны яркостные температуры параметров Стокса I и V: TImax и TVmax. Вычисления по известным формулам, приведенным в [11, 12] в соответствии с данным методом, сделаны с помощью программы IDL 6.1.

Графики зависимостей T I max ( B ) для длин волн 5.2 см (ССРТ) и 1.76 см (NoRH) приведены на рис. 2.

Видно, что на разных длинах волн при малых изменениях поля вблизи среднего значения 3000 Гс мы получим разные величины амплитуд изменений яркостных температур: на 1.76 см нелинейность выражена сильнее на этом участке кривой.

Пусть B изменяется как B = B ₀ ( 1 + 0.01sin 2n t(T )

с периодом T = 200 мин. Тогда мы получим синфазные медленные колебания T_{I max} и T_{V max} с таким же периодом на длинах волн 5.2 и 1.76 см (рис. 3–7).

Рисунки 3–7 показывают, что небольшие изменения B (~1 %) приводят к изменениям T_{I max} и T_{V max} на длинах волн 5.2 и 1.76 см, которые заметно превышают чувствительность радиогелиографов, равную 1500 и 400 K соответственно.

Предполагая циклотронный механизм излучения для обеих длин волн, мы могли бы зарегистрировать более сильные осцилляции радиоизлучения на 1.76 см (~ 10 %) , чем на 5.2 см (~1 %) .

где Т ₀ = 6000 K - температура фотосферы, А = 2 - 10 6 K, l = 2 - 10 8 см, z 0 =7 - 10 8 см - численные параметры в данной модели температурного распределения. Распределение концентрации частиц над фотосферой можно найти по барометрической формуле и уравнению идеального газа:

N ( z ) = N ₀ exp

{ Ц g z dz ' ) ^T 0 ---------------- -------------,

( R 0 T ( z ') J T ( z )

где N ₀ =10¹² cм^–3 – концентрация водорода на фотосфере, g – гравитационное ускорение, µ – молярная масса водорода, R – газовая постоянная.

Форма гироуровней r = r _s (θ, x , y ), где θ – угол зрения, равный гелиодолготе, может быть найдена из выражения для магнитного поля монополя путем численного решения уравнения ω = s ω B ( B ( r , θ, x , y )), где s – номер гармоники излучения. Используя эту зависимость, можно вычислить угол α между направлением распространения излучения и магнитным полем, магнитную длину L_B , температуру и концентрацию на гироуровнях, а также другие величины, которые позволяют определить оптическую толщину τ _is , яркостные температуры T I , T V параметров Стокса I и V .

Для микроволновых источников в спокойной стадии развития активной области удобно при обработке данных вырезать радиоисточник на двумерных картах распределения T I и T V , находить в вырезанном фрейме пиксель с максимальными яркостными температурами T I max , T V max и отслеживать изменения этих величин во времени. Поэтому при мо-

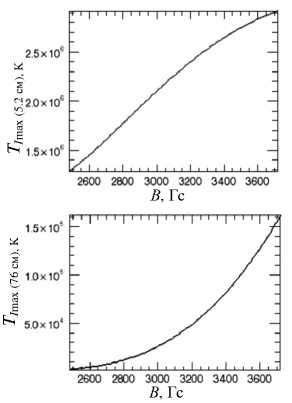
Рис . 2. Зависимость максимального значения яркост ной температуры параметра Стокса I ( T_{I max} ) от напряжен ности поля B : а – для 5.2 см ; б – для 1.76 см .

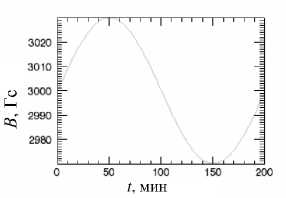
Рис . 3. Периодические изменения магнитного поля пятна В с амплитудой ~1 % от B ₀ (30 Гс ).

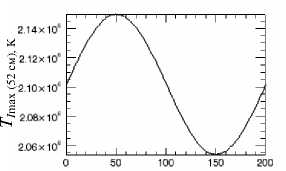
t , мин

Рис . 4. Периодические изменения T_{I max} на 5.2 см с ам плитудой 50000 K (~ 2 % от < T I max >).

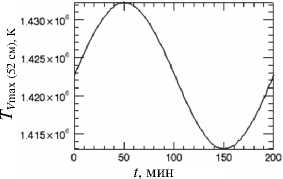
Рис . 5. Периодические изменения T_{V max} на 5.2 см с ам плитудой 9000 K (~ 0.6 % от < T V max >).

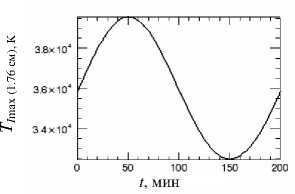
Рис. 6. Периодические изменения TImax на 1.76 см с амплитудой 3500 K (~ 10 % от ).

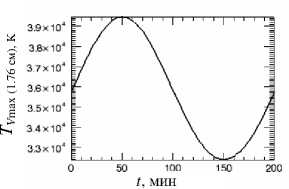
Рис . 7. Периодические изменения T_{V max} на 5.2 см с ам плитудой 3600 K (~ 10 % от < T V max >).

Расчеты, проведенные в [13], показывают, что диапазон частот сантиметрового диапазона критичен к выбору модели атмосферы над активной областью. Показано, что в случае возмущения магнитного поля в радиоисточнике МГД-волнами (альфве-новскими или быстрыми магнитозвуковыми) с периодом более 20 мин колебания дифференциальной характеристики радиоизлучения – наклона спектра (разности интенсивностей на двух близких частотах) – на втором и третьем гироуровнях происходят син-фазно. Но оценка плотности потока МГД-волн над пятном по наблюдательным данным оказывается заведомо ниже расчетных величин, необходимых для возбуждения наблюдаемой амплитуды флуктуаций наклона спектра. Эта трудность в интерпретации наблюдаемых долгопериодических флуктуаций наклона спектра распространением МГД-волн может быть вполне объяснима тем, что подобная модуляция вызвана не МГД-волнами, а собственными долгопериодными колебаниями пятен.

Используя вычисленные зависимости в нашей модели, мы можем искать корреляции изменений магнитного поля и поля лучевых скоростей, определяемого оптическими методами на уровне фотосферы пятна, с вариациями интенсивности и поляризации, полученными по данным современных радиогелиографов ССРТ и NoRH, работающих с большим перекрытием по времени. Исследование долгопериодических колебаний пятен в радиодиапазоне открывает новые возможности в диагностике их физических свойств.

Работа частично поддержана грантами РФФИ: 0602-16295, 06-02-39029, 07-02-01-066; 05-07-90209в; 0602-16268, 07-02-00379, 06-02-16981-А, а также программами Президиума РАН № 16 и ОФН РАН № 16.