Об аналитическом продолжении кратного степенного ряда с помощью m-однородных полиномов матричным методом в обобщенную звезду Миттаг-Леффлера

В одномерном случае продолжение степенного ряда в максимальную звездную область впервые было построено Миттаг-Леффлером, поэтому такая область называется звездой Миттаг-Леффлера или главной звездой данного степенного ряда. Известны обобщения этого факта на случай нескольких переменных для класса звездных областей. В связи с новой волной интереса к суммированию расходящихся рядов, являющихся формальными решениями дифференциальных уравнений (например, [1–3]), в настоящей работе предлагается матричный метод, суммирующий ряд из полиномов в параболической звезде Миттаг-Леффлера или х -звезде Миттаг-Леффлера. Параболическая звезда Миттаг-Леффлера является естественным обобщением обычной звезды, но не всегда с ней совпадает. В работе приводится пример функции, у которой (1, 2)-звезда не совпадает с главной звездой.

Пусть x е R " ; x 1 >  0, ..., x n >  0. Множество G в C ⁿ назовем х -параболическим, если вместе с каждой точкой z ⁰ = ( z 0 , ..., z 0 ) в множестве G содержится х -отрезок

{ z е C" : z 1 = z 0 t x ¹ , ..., z n = z 0 _nt xⁿ : V t е [0,1]} c G .

Область D из C ⁿ с центром в точке а назовем обобщенно m -круговой m = ( m 1 , ..., m_n ) m ^ е N и m ₁, ..., m_n взаимно просты), если вместе с каждой точкой z 0 е D область D содержит точки

{z е C" : z1 = a1 + (z^ - a1)e1™1, ..., z„ = a" + (z0 - a")e™"e; V0е [0,2n]},

• т. е. образ окружности, проходящей через точку z ₀ . Если область D содержит образ всего круга, то об-

• the main star, analytic continuation, summation of multiple

ласть называется полной, т. е. вместе с точкой z ₀ содержит множество

{z е C" : z1 = a1 + (z10 - a1)Xm1, ..., z" = a" + (z0 - a" )X™"; VX ^X\< 1}.

Если функция f ( z ) голоморфна в некоторой окрестности начала координат в C ⁿ , то максимальную х -параболическую область G_f^x , в которую голоморфно можно продолжить функцию f , назовем х -параболической звездой Миттаг-Леффлера функции f или просто х -звездой.

В случае одного переменного всякая х -звезда Мит-таг-Леффлера совпадает с обычной звездой Миттаг-Леффлера или главной звездой данного степенного ряда. В случае многих переменных это не так.

Пример . Функция f ( z 1 , z ₂) = (1 - z ₂ + z 1 ²) ^{- 1} имеет главную звезду, отличную от (1,2)-звезды Миттаг-Леффлера. Это вытекает из того, звезда функции f в вещественном подпространстве C ² не совпадает с (1,2)-звездой в силу особенностей функции f .

Таким образом, можно указать функцию, у которой (1, 2)-звезда несет больше информации, чем главная звезда или (1,1)-звезда.

Известно, что область сходимости n -кратного степенного ряда

f ^{( z} 1 ... z " ) = E a kv-k"^z1 k ¹ ... ^z" ^k " ⁽¹⁾ \| k \\ > 0

является полной логарифмически выпуклой n -круговой областью, содержащей нуль. Если члены ряда (1) переставить, то его область сходимости может измениться.

Классическая теорема о переразложении ряда (1) по однородным полиномам приводит к круговым областям и имеется, например, в [4; 5].

Фиксируем m = ( m ₁,..., m n ), m ^ e N n и m ₁, ..., m n взаимно просты. Все члены ряда (1), у которых мультииндексы удовлетворяют уравнению

< k , m >= k₁ m₁ + ... + k n m n = v , сгруппируем в полиномы

< k , m >= v

Полиномы P v ( z ) удовлетворяют равенству P v ( t^mz ) = P_v ( t m¹ z ₁, ..., t mn z n ) = t^vP_v ( z ) для произвольных V t e C ; V z e C n . Такие полиномы P v ( z ) обычно называют ( m , v )-однородными или ( m , v ^взвешенными. Они являются естественным обобщением однородных полиномов.

Тогда функцию f, заданную рядом (1), можно представить в виде да f (z) = Е Pv (z).                  (2)

v = 0

Область сходимости ряда (2) - это максимальная m -круговая область, которую можно поместить в область голоморфности функции f .

Область сходимости ряда (2) - полная обобщенно m -круговая область D в C n . Верно и обратное утверждение, т. е. по аналогии с теоремой 3 из [4, с. 53], справедлива Теорема 1.

Теорема 1. Любую функцию f, голоморфную в полной обобщенно m -круговой области D в C n с центром в нуле, можно разложить в ряд (2) по m -однородным полиномам, который будет сходиться равномерно на любом компакте из D .

Доказательство . Ряд (1) абсолютно сходится с достаточно малой окрестности U начала координат в D , следовательно, в этой окрестности будет сходиться и ряд (2). Возьмем произвольную точку z ₀ из области D , так как область D , является полной обобщенно m -круговой, существует X ₀ e C : w ₀ = Х ₀ ^mz ₀ e U . Ряд (2) сходится в точке w ₀ и задает при достаточно малых X голоморфную функцию ф :

да f (w) = f (X mz) = Е Pv (X mz) = Ф(Х) v=0

Разложение функции ф в ряд Тейлора в начале координат имеет вид да                      да

ф ( Х ) = Е P v ( X m z ) = Е P v ( z ) X^v        (3)

v = 0              v = 0

Функция f голоморфна в некоторой окрестности точки z , поэтому функция ф , как суперпозиция голо-морных функций, голоморфна при | X | < 1 + е для некоторого е >  0, следовательно ряд (3) будет сходиться при X = 1, что, в свою очередь, означает сходимость ряда (2) в точке z .

Точка z принадлежит D с некоторой окрестностью U ( z ), для всех точек U ( z ) можно повторить рассуждения, приведенные выше, поэтому ряд (2)

сходится в некоторой окрестности точки z , лежащей в D .

Пусть K компактно лежит в D . Каждому z e K соответствует некоторая достаточно малая окрестность U ( z ) c D , в которой ряд (2) будет сходиться абсолютно и равномерно для точек U ( z ). Совокупность U ( z ) является открытым покрытием K ; выбирая из этого покрытия конечное подпокрытие, получим равномерную сходимость ряда (2) во всех точках K . Теорема 1 доказана.

Зная разложение функции f по m -однородным полиномам с помощью матричного метода можно восстановить значения функции f всюду в m -звезде G m Миттаг-Леффлера функции f

Теорема 2. Пусть функция f задана рядом (2) в некоторой непустой окрестности начала координат, m e Nn и G = Gm - ее m-звезда Миттаг-Леффлера. Тогда существует такая бесконечная матрица комплексных чисел B := {b0l,...,bk l}/=0, что справедлива формула: да f (z) = Е b0,Л( z) +... + bl, 1P( z).        (4)

l = 0

Причем сходимость - равномерная на любом компакте в G , и матрица B не зависит от функции f , а зависит лишь от области G .

В случае одного переменного формула (4) имеется в двухтомнике Маркушевича [6, с. 495] и называется разложением Миттаг-Леффлера. В случае многих переменных для класса звездных областей теорема 2 доказана М. Довнарович по схеме, предложенной Си-чаком [7].

Доказательство. Для произвольной точки z0 из области G найдется окрестность этой точки V(z0), компактно лежащая в G, и жорданов путь Sz0 в C, охватывающий точки 0 и 1, такие, что к Jz e Cn : Z = (Xmz) = (Xm1 z1, ..., X”4),!

K : =

[X e S z 0 ; z e V ( z 0 )                        J

и K компактно лежит в G .

Тогда по формуле Коши имеем:

f ( z ) = -Lj f ( X ^mz ) EX = 2 n i "            X - 1

Sz 0

2 n i

J   f ( X m z ) 1 1

Sz 0            V

-

X

- 1

dX

.

X

Так как множество S_z 0 : = { X ¹ : X e S_z 0 } компактно лежит в { C \[1, да ] } , то в силу известной теоремы Рун-

Z 1 \-1

ге функцию 1 1 - х I можно равномерно аппрокси-

,,          1      _ s мировать полиномами Ml от x на Sz0

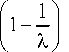
ГО

= Z Ml l = 0

I

Подставляя (6) в (5) заметим, что из равномерной сходимости ряда (6) на любом компакте из области { C \[1, го ] } , допустимо почленное интегрирование.

Полиномы из ряда (2) можно найти по формуле

Pi ( z ) = f a mz ) % 2 n i •              I ^{l + 1}

Sz ₀

Возьмем в качестве матрицы B коэффициенты полинома M_l . Полиномы M_l построены конструктивно в [6, с. 497] по методу П. Пенлеве и могут быть использованы вне зависимости от функции f . Теорема 2 доказана.