Об аналитическом решении уравнения движения электронов в цилиндрическом зеркале при учете электронов, имеющих азимутальную компоненту скорости

Задача решения уравнения движения электронов в цилиндрическом зеркале (ЦЗ) при учете электронов, имеющих азимутальную компоненту скорости, рассматривалась во многих работах. Среди этих работ можно выделить работы [1–4], в которых, на наш взгляд, сделан основной вклад в решение проблемы. В этих работах удалось свести уравнения движения, записанные в цилиндрической системе координат, к зависимости времени от радиальной координаты в виде интегрального представления (в обозначениях работы [5])

к точке эмиссии R ₀ , ϑ — угол между нормалью к плоскости XY (осью Z ) и вектором скорости, φ — азимутальный угол, отсчитываемый вокруг

точки R ₀ , между осью Y и проекцией V_xy вектора

скорости на плоскость XY;

k -— ( E/u ) ln ( : 2^ ) ;

E — кинетическая энергия электронов до влета

rm

T=2I

V . Г

dr sin2 9 — sin2 9 • sin2 ф -f—)

г л

, (1)

—

-ln ~

k

r

V ri 7

где T — время пролета электронов через дисперсное пространство; r_m — точка наибольшего удаления электронов от внутреннего цилиндра, являющаяся корнем функции, стоящей под знаком радикала

в дисперсное пространство; r ₁ , r ₂ — радиусы внутреннего и внешнего электродов ЦЗ; U — потенциал на внешнем электроде ЦЗ, имеет отрицательный знак (в данной работе U = –100 В); на внутреннем электроде ЦЗ установлен потенциал, равный нулю.

Решение уравнения движения в его преобразованном виде (1) требует решения двух задач: нахождения корня уравнения (2) и собственно решения (интегрирования) уравнения (1).

Представленная статья является продолжением работ [5, 6], в которых с помощью расчета траекторий изучались особенности функционирования цилиндрического зеркала. В этих работах числен-

ными методами находились такие величины, как

sin² ϑ

— sin² 9 • sin²

—

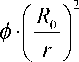
1_ln k

r

V ri 7

= 0.   (2)

Начальные условия для уравнений движения: R ₀ — радиус для точки вылета электронов из источника; V ₀ — скорость электронов до входа в дисперсное пространство; ϑ , φ — углы в локальной сферической системе координат, привязанной

распределение моноэнергетичного пучка электронов по поверхности цилиндра, содержащего выходную диафрагму (ЦВД), распределение светосилы по поверхности эмиттера, аппаратная функция и прочие. В этих условиях важно иметь возможность проверять проводимые вычисления. Одним из возможных способов проверки получаемых результатов является применение различных методов расчета.

В работах [5, 6] для каждой траектории сперва вычислялось расстояние наибольшего удаления

электронов от внутреннего цилиндра ( r_m ), далее проводилась проверка неравенства r m <  r ₂, которое означает, что электрон в процессе своего движения через дисперсионное пространство не касается верхнего электрода. И после этого для вычисления интеграла в (1) было применено правило вычисления [7], имеющее наивысшую алгебраическую точность (типа Гаусса).

Другой метод расчета траекторий — расчет методом Рунге—Кутта [8] в трехмерном декартовом пространстве. Недостатком метода Рунге—Кутта является относительно большое время счета. Cравнение метода интегрирования уравнения (1) и метода Рунге—Кутта показало, что при сравнимой точности расчета последний метод работает до 3 порядков медленнее [5]. Поэтому нет возможности применить метод Рунге—Кутта параллельно с методом (или вместо него) интегрирования уравнения (1) для всего массива вычислений, таких как в [5, 6]. А можно применять только в некоторых точках. Сравнение точности этих двух методов, проведенное в работе [5], показало совпадение результатов с точностью не хуже 10 ^{- 8} м.

Еще одним методом решения уравнений движения является разложение редуцированных к виду (1) уравнений движения в ряд Тэйлора. В работе [1] было применено разложение выражения, стоящего в правой части (1), в ряд Тэйлора по малому углу γ с точностью до членов, порядка tg²( γ ) , где γ –– угол, пропорциональный азимутальному углу. С одной стороны, в этом случае нельзя требовать изотропности начального распределения электронов по этому углу. С другой стороны, остается вопрос: достаточно ли разложение до членов порядка tg² ( γ ) для получения приличных по точности результатов. В работе [5] в каждой точке эмиссии рассматривалась (местная) сферическая система координат (СК). Поэтому для этого случая изотропное распределение эмитируемых электронов является обоснованным.

Чтобы искать решение выражения (1) в виде разложения в ряд по углу φ , необходима малость этого угла. Поэтому следует изучить телесный угол ( ϑ , φ ) , под которым из точки эмиссии видна выходная диафрагма (ВД). С точностью до константы этот телесный угол равен светосиле [9].

ТЕЛЕСНЫЙ УГОЛ (СВЕТОСИЛА)

Все вычисления в данной работе проведены для ЦЗ с радиусом внутреннего цилиндра r = 2 см и радиусом внешнего цилиндра r ₂ = 5 см. На внутреннем цилиндре установлено напряжение, равное нулю, на внешнем цилиндре — U = - 100 B.

Для фиксированных значений R ₀ , E и для каждого x ( x = cos( S )) рассчитываем траектории при разных значениях угла φ методом, описанным в работе [5]. В результате получаем значения z -координат точек пересечения траектории и цилиндра, содержащего ВД, L_k ( x_k , φ_k ). Предположим, что определено некоторое положение ВД: L _B , L _E — значения расстояний вдоль оси Z от источника до ближнего и дальнего краев ВД. Тогда мы имеем возможность сравнивать два последовательных значения L k и L k _{+ 1} с L B и L E . Если при каком-то значении индекса k выполняется неравенство L_k <  L _в <  L_{k + 1}, то далее простой линейной интерполяцией можно вычислить угол φ _B , стартовав с которым (и при фиксированных значениях x , R ₀, E ) электрон попадет в передний край ВД:

Ф в = Ф к + ( Ф к + 1 - Ф к ) L L ^Lk + 1 ^- L k

С дальним краем ВД вычисления производятся вполне аналогично при L_k <  L E <  L_{k + 1} :

^Ф Е = ^Ф k ^{+ ( Ф} k + 1 - ^Ф k ) _т ^L E    ^Lk_T

^Lk + 1 - ^Lk

В результате мы получаем φB(x) и φE (x) — значения азимутального угла, стартовав с которым, электроны попадают в ближний и дальний края ВД. Разность ФЕ (x) - Фв (x) дает нам диапазон азимутальных углов, стартовав в котором, электроны попадают на детектор. Телесный угол изображается некоторой областью на плоскости (ϑ,φ), ограниченной линиями. В нашем случае это линии φB (ϑ) и φE (ϑ) . Вычисляется телесный угол как двойной интеграл U sin Э^Ф dS по этой облас-

ти. Поэтому нахождение этого телесного угла (зависимости φB,E (ϑ) ) может служить еще одним ме- тодом вычисления светосилы, светимости и т.д.

Некоторые возможные виды телесного угла (ТУ) представлены на рис. 1–3, на которых в различной комбинации варьируются четыре параметра: P_y — радиус цилиндра, содержащего ВД; E — энергия электронов; R ₀ — радиус для точки эмиссии; d _Diaphr — ширина ВД. При рассмотрении рис. 1–3 следует иметь в виду, что на этих рисунках приведена только половина телесного угла. Полный телесный угол симметричен относительно оси ϑ ( Ф = 0 ° ). На рисунках линии, ограничивающие телесный угол, имеют маркировку из 2 символов:

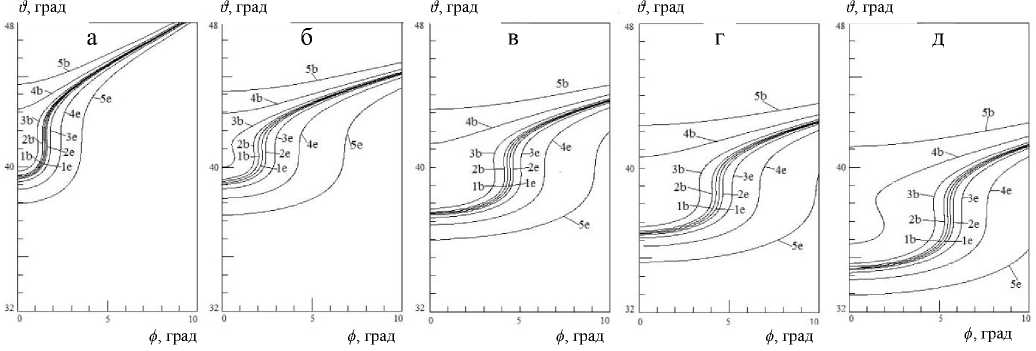
Рис. 1 . Телесный угол в зависимости от ширины выходной диафрагмы для разных значений радиуса ЦВД. Пояснение в тексте

1-й — цифровой (от 1 до 5) на рис. 1 указывает на ширину ВД, 2-й буквенный — b или e — соответствует индексам B, E в формулах (3), (4). На рис. 1 показан телесный угол для значений ширины выходной диафрагмы 1 — d _Diaphr = 1 мкм, 2 — d _Diaphr = 3.3 мкм, 3 — d _Diaphr = 10 мкм, 4 — d _Diaphr = = 33 мкм, 5 — d _Diaphr = = 100 мкм при разных значениях радиуса ЦВД для "окон" рис. 1: а — P_y = 1 мм , б — P_y = 5 мм , в — P_y = 10 мм , г — P_y = 15 мм , д — P_y = 20 мм . Энергия установлена на величину E = E_p , при которой максимум распределения электронов по ЦВД находится на ЦВД с радиусом P_y : для а — E_p = 133.04 эВ, для б —

E_p = 125.54 эВ, для в — E_p = 114.96 эВ, для г — E_p = = 102.46 эВ, для д — E_p = 87.34 эВ (значения E_p взяты из работы [5]), точка эмиссии R ₀ = 5.01 мм выбрана посредине ширины кольца эмиссии.

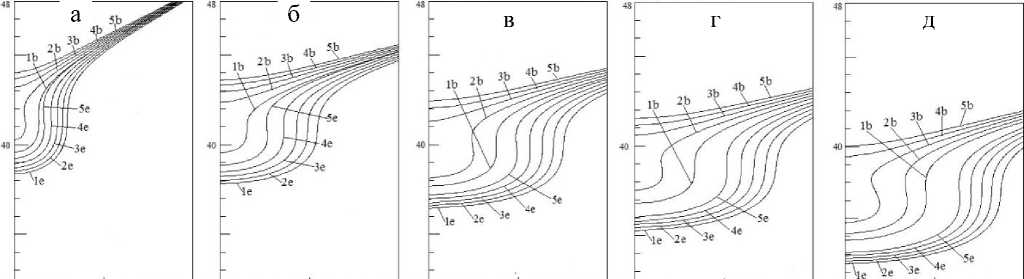
На рис. 2 представлены результаты вычисления телесного угла в зависимости от энергии электронов в окрестности энергии E_p . 1-й символ в маркировке линий на рисунке: 1 — E = E_p – – 0.02 эВ, 2 — E = E_p – 0.01 эВ, 3 — E = E_p , 4 — E = E_p + 0.01 эВ, 5 — E = E_p + 0.02 эВ. В "окнах" рисунка кривые при значении радиуса ЦВД: а — P_y = 1 мм , б — P_y = 5 мм , в — P_y = 10 мм , г — P_y = 15 мм , д — P_y = 20 мм . О величине E_p для

ϑ , град                       ϑ , град                       ϑ , град                       ϑ , град                        ϑ , град

О                    5                   10 О                    3                    10      0                    3                   10 О                    3                   10 j                                         I

ϕ , град                          ϕ , град                         ϕ , град                       ϕ , град                          ϕ , град

Рис. 2. Телесный угол в зависимости от энергии электронов в окрестности E = E_p для разных значений радиуса ЦВД. Пояснения в тексте

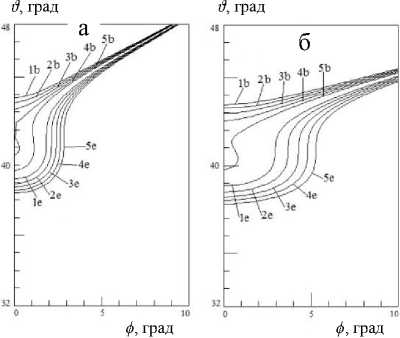
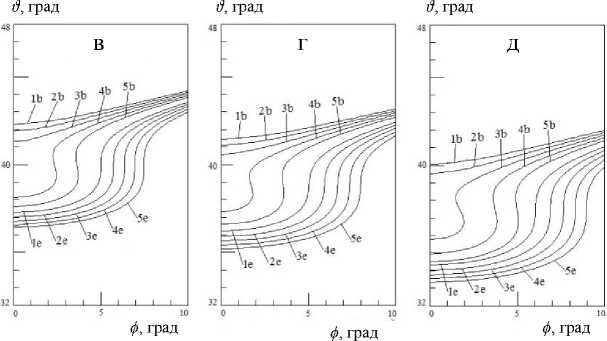
Рис. 3 . Телесный угол в зависимости от положения точки эмиссии для разных значений радиуса ЦВД. Пояснения в тексте

каждого P_y и величине R ₀ см. пояснения к рис. 1. Ширина ВД выбрана d _Diaphr = 33 мкм.

На рис. 3 приведены результаты вычисления телесного угла в зависимости от положения точки эмиссии: 1b, 1e — R 0 = 5.00 мм; 2b, 2e — R 0 = = 5.005 мм ; 3b, 3e — R 0 = 5.01мм ; 4b, 4e — R 0 = = 5.015 мм; 5b, 5e — R 0 = 5.02 мм для разных значений радиуса ЦВД; "окна" рисунка: а — P y = 1 мм, б — P y = 5 мм, в — P y = 10 мм, г — P y = 15 мм , д — P y = 20 мм. При этом ширина ВД d Diaphr = 33 мкм, энергия электронов E = E_p — энергия, при которой максимум распределения электронов по ЦВД находится на ЦВД с радиусом P_y (см. пояснение к рис. 1).

При рассмотрении рис. 1–3 с телесным углом важно понять, что делать, когда φ _E ( x ) существует, а φ _B ( x ) — нет. Например, на рис. 1 кривые 5b и 5e. В диапазоне углов 38 ° <  9 <  43 ° кривая 5е существует, а 5b — нет. При ф = 0 кривая 5е упирается в ось 9 в районе 9 = 38 ° . Этому соответствует попадание электронов в дальний край ВД. При ф = 0 и 9 ~ 43 ° электроны попадают в ближний край ВД. А в промежутке 38 ° <  9 <  43 ° точка попадания электронов перемещается от дальнего края ВД к ближнему. Так что в этом промежутке угла ϑ в качестве φ _B ( x ) можно использовать ф в = 0.

Отметим, что на рис. 1–3 функция φ ( ϑ ) однозначна, а функция ϑ ( φ ) не является однозначной.

НАХОЖДЕНИЕ НАИБОЛЬШЕГО УДАЛЕНИЯ ЭЛЕКТРОНОВ ОТ ВНУТРЕННЕГО ЦИЛИНДРА

Наибольшее удаление электронов от внутреннего цилиндра определяется как решение уравнения (2) и выражается через функцию Ламберта [10]

rm = rm 0 Х х exp <

LambertW 2

Г .        . г2 А1

- 2sin² 9 - sin² ф - -0- > v                      r m 0 J,

, (5)

где r m о = r i ' e k ' sin ⁹ — наибольшее удаление электронов от внутреннего цилиндра при ф = 0, т.е. без азимутальной компоненты скорости (коэффициент k определен выше), напомним, что для электронов U имеет отрицательный знак и в данной работе U = - 100 в.

Решение уравнения движения мы собираемся искать в виде разложения в ряд по углу φ (или по некоторой функции от φ). Поэтому вполне логич- но расстояние rm также искать в виде разложения в ряд. Для функции Ламберта существует разложение в степенной ряд [10] по переменной x = - 2sin2 9 - sin2 ф - 0- в окрестности x = 0: rm20

LambertW( x ) =

2   3 3   8 4   125 5

= x - x + —x —x +--x--x .(6)

2     3     245

Сравнение расстояния r_m , вычисленного по

Табл. 1. Расстояние r_m , вычисленное по формулам (5, 6), и это расстояние, полученное при решении уравнения (2) методом половинного деления (см. [5]). (Все расстояния приведены в мм. Пояснения в тексте.)

Метод, степень ряда разложения	ϕ = 0°	ϕ = 5°	ϕ = 10°	ϕ = 15°	ϕ = 20°
Работа [5] x 1 + x 2 + x3 + x4 + x5	32.6834057772 — ˮ — — ˮ — — ˮ — — ˮ — — ˮ —	32.6805402909 32.6805407933 32.6805402910 32.6805402909 32.6805402909 32.6805402909	32.6720264516 32.6720343726 32.6720264598 32.6720264516 32.6720264516 32.6720264516	32.6581101140 32.6581492394 32.6581102048 32.6581101142 32.6581101140 32.6581101140	32.6391943608 32.6393138103 32.6391948449 32.6391943631 32.6391943608 32.6391943608

формулам (5, 6), и этого расстояния, полученного при решении уравнений (2) методом половинного деления (см. [5]), приведено в табл. 1 для значений угла ϕ : 0, 5, 10, 15, 20°.

В строке "Работа [5]" даны результаты решения уравнения (2) методом половинного деления (см. работу [5]). Строки, лежащие ниже, представляют результаты, полученные с применением формул (5, 6). В строке "  x ¹ " приведены результаты, для получения которых в формуле (6) оставлен только член с x в 1-й степени. В строке "+ x ² " оставлены члены с x в 1-й и 2-й степенях. И так — до x в 5-й степени. В столбце ф = 0 ° все результаты одинаковы, т.к. при этом угле r m = r m 0 . При больших углах φ результаты применения формул (5, 6) показывают, что количество членов, необходимых для получения хорошего результата, невелико. Так, для ф = 20 ° использование в формуле (6) членов до x ⁴ дает результат с точностью 10 знаков после запятой (в мм), не отличающийся от результата, полученного с помощью алгоритма работы [5]. Применение в (6) членов с x ⁵ дает результаты, не отличающиеся от результатов с x ⁴ . Поэтому результаты с x ⁶ не приведены. Ясно видно, что для получения r_m с относительной точностью не хуже 10 ^{- 10} в формуле (6) достаточно оставить члены до x ³ включительно.

РЕШЕНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ

Обратимся к уравнению (1). Нас интересует присутствующий в этом уравнении в качестве параметра азимутальный угол φ (в sin² φ ). Удобно выбрать в качестве параметра разложения в ряд

x = sin² ф . Этот параметр входит не только в подынтегральное выражение, но и в верхний предел интегрирования.

Первый коэффициент разложения правой части уравнения (1) в ряд (коэффициент при x ⁰ )

r m 0

T (0) =—• f

V _{0    r 1}

d r

/ Л

sin² 9 -

-ln -

k

r

I rl )

представляет собой время прохождения дисперсного пространства электронами, имеющими нулевую азимутальную компоненту скорости. Это выражение было рассмотрено в работе [11]. Для него легко получить

T (°> = ±Jk r m 0 p e- y ² d y

V 0       0

Стоящий в правой части интеграл может быть сведен к функции ошибок, для которой есть интерполяционные формулы. Но если вычислить этот интеграл по формуле Гаусса, то точность можно получить заметно лучшую.

Второй коэффициент разложения (коэффициент при x ¹ ):

T ⁽¹⁾ = A. k ^3/2 . sin² 9 . r 2 x

^V 0                 ⁰

x

r m 0

I— r ^{1 2} . r ² .

V

d r

?

k • sin² 9 - In

V

3/2

r I

V rl))

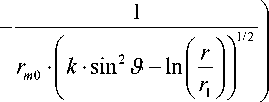
В результате получаем

T ⁽¹⁾ =

Подобно работе [11], делаем замену переменной

= — k ^3/2 • sin² 9 ^ • e^p x — + 2 • Daw( p ) I . (9)

V 0               r m 0        V p             )

r I y = k • sin2 9 - In — . Отсюда получаем r = r • e

V r )

kkx - yy

Вполне аналогично получаем выражения для следующих коэффициентов ряда:

= r_{m 0} • e ^y , d r = - 2 y • r_{m 0} • e ^y • d y и выражение для

T ⁽¹⁾ преобразовывается:

T (2) =     • k ^5/2 • sin⁴ 9 ^ r^ • e^{3p 2} x

^{2 V} 0                ^rm 0 ³

T (1) = — • k^3/2

V 0

2 P у ²

• sin² 9 * — • f—2-d y - ^rm о V о У

I - ^yy '0 )

- 3^ V ³ p

— +

p

I

4 V3 • Daw(V3 p ) )

Видны две бесконечности: при нижнем пределе интегрирования и во втором члене, стоящем в скобках. Представим выражение, стоящее в скобках, в виде предела

T <³> = — • k ^7/2 • sin⁶ 9 • -r °- • e^{5p 2} x 4 V 0                 r m 0 ⁵

x

^p y ²

e  _{d y}

₀ y ²

Л

p

y

(r

= lim

£ ' 0

VV

y

y ' 0 )

e y ²

+

y

= lim f e y d y £ ' 0 J y ²

£ ' 0

V ^£

I ^{p n} • b^{erf (i} y ) ) _£

—

y y'£ )

Л

£

)

Видно, что члены с — £ сокращаются, erf(i0) = 0

и после перехода к пределу остается только

г

V

e^{p 2}

+

p

I • 1 • e ^rf(i p ) )

где второй член равен

x

2               22

(см. [10]) - 2 ep • Daw( p ), Daw( x ) = e J e • d t — 0

функция (интеграл) Доусона, для которого существует интерполяционная формула и можно получить значения численным интегрированием.

-

V ⁵ p

—- — + 40 V5 • Daw( V5 p )

3 p ³ 3 p

Полное время пролета электрона через дис-

персное пространство

T = T <⁰⁾ + T ⁽¹⁾ • sin² Ф + T <²⁾ • sin⁴ Ф + T <³⁾ • sin⁶ Ф . (12)

Расстояние вдоль оси Z , проходимое электроном при пролете через дисперсное пространство,

L = T • V ₀ • cos( 9 ). (13)

Сравнение расстояния, пройденного электроном в дисперсном пространстве, полученного прямым интегрированием в формуле (1) (см. работу [5]), с этим же расстоянием, вычисленным по формулам (12, 13), для углов вылета ϕ = 0, 5, 10, 15, 20° приведено в табл. 2. В первом столбце применяются следующие обозначения: "Работа [5]"— в этой строке приведены результаты прямого интегрирования в формуле (1) (см. работу [5]).

Табл. 2. Сравнение результатов решения уравнения движения в приведенном к интегральному виду (1) методом прямого интегрирования (см. работу [5]) и методом разложения в ряд (7–13). Подробности в тексте

Метод, степень ряда разложения	ϕ = 0°	ϕ = 5°	ϕ = 10°	ϕ = 15°	ϕ = 20°
Работа [5]	63.81075911	63.80767615	63.79851575	63.78354129	63.76318471
sin0 ϕ	63.81075939	63.81075939	63.81075939	63.81075939	63.81075939
+sin2 ϕ	— ˮ —	63.80767686	63.79852295	63.78357579	63.76328954
+sin4 ϕ	— ˮ —	63.80767642	63.79851603	63.78354164	63.76318540
+sin6 ϕ	— ˮ —	63.80767642	63.79851603	63.78354156	63.76318499

В строке "sin⁰ ϕ " приведены результаты, для получения которых в (12) оставлен только член с T ⁽⁰⁾. В строке "+sin² ϕ " — оставлены T ⁽⁰⁾ + T ⁽¹⁾sin² ϕ и т.д. до "+sin⁶ ф ". В столбце с ф = 0 ° по формулам (12, 13) получаются результаты с отсутствующей азимутальной компонентой скорости. Понятно, что они должны быть одинаковы. Результаты, приведенные в строке "+sin⁶ ϕ ", оказываются совпадающими с результатами строки "+sin⁴ ϕ " с точностью 1 - 10 ^{- 6} мм вплоть до ф = 20 ° . Это говорит о том, что если оставить в формуле (12) члены вплоть до T ⁽³⁾ , то результат будет иметь относительную точность не хуже 10 - 8 .

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Изучение телесного угла, стартовав в пределах которого электроны попадают на детектор, показало, что вдоль диапазона изменения энергии и вдоль диапазона изменения радиуса эмиссии, наблюдается максимум телесного угла. Из этого следует, что возможно получение максимума светосилы.

Из рис. 1–3 видно, что выбор диапазона изменения угла ϑ может привести к определенности диапазона изменения угла φ . Можно выделить три диапазона изменения углов ( ϑ , φ ) : на первом, начальном отрезке, кривая φ _E( x ) перпендикулярно отходит от оси ϑ и далее идет почти перпендикулярно к оси ϑ . После некоторого переходного участка наблюдается отрезок, на котором φ _E ( ϑ ) почти параллельна оси ϑ . На третьем участке наблюдается значительный рост φ _B( x ) и φ _E( x ) . Причем с увеличением P_y наклон кривых φ _B ( x ) и φ _E ( x ) увеличивается. Исключением из этого является φ _B ( x ) для самых больших значений ширины ВД (33 мкм и 100 мкм), когда φ _B ( x ) не имеет почти горизонтальной части (кривые 4b и 5b для P y <  15 мм и кривая 5b для P y = 20 мм).

Весьма интересный эффект можно наблюдать на рис. 1. Если рассматривать разность ф_Е ( 9 ) - ф_в ( 9 ) на участке изменения 9 , на котором график функции φ _E ( ϑ ) почти параллелен оси ϑ , то видно, что ф _5е - ф _5Ь растет при росте P y , Ф 4 _е — ф _4Ь растет от рис. 1, а, до рис. 1, г, а на рис. 1, д, эта разность меньше, чем на рис. 1, г. Разность ф _3е - ф _зь имеет максимум при P y = 5 мм.

На рис. 2, б–д хорошо видно, что кривые 1е–5е идут с почти равным сдвигом друг относительно друга. А вот разница ф - фв сперва увеличивается (с увеличением энергии) от 1-й к 3-й кривой и, начиная с третьей кривой, уменьшается. Т.е. на этом рассматриваемом нами отрезке изменения энергии телесный угол и светосила имеют максимум вблизи E = Ep .

По-другому ведет себя разность ф _Е - ф на начальном участке изменения угла ϑ , там, где φ _B отсутствует и приходится брать ф _в = 0. На этом участке φ _E растет с ростом энергии и поэтому телесный угол и светосила растут.

На третьем участке изменения угла ϑ визуально трудно определить, как изменяется разность ф _Е - ф _в с ростом энергии.

На рис. 3 ситуация похожа на рис. 2. Начиная с рис. 3, б, графики φ _E ( ϑ ) выглядят сдвинутыми друг относительно друга на примерно равное расстояние ( А ф ~ сonst). А вот между графиками ф _в расстояние неодинаково, и сами графики не выглядят подобными. Это позволяет говорить о том, что разница ф _Е - ф _в имеет максимум вблизи R ₀ = 5.01мм, т.е. вблизи середины ширины кольца эмиссии.

Нахождение радиуса наибольшего отклонения электронов от внутреннего цилиндра ЦЗ методом решения уравнения (2) и последующим разложением функции Ламберта в степенной ряд показало хорошую сходимость и хорошее соответствие с результатами, полученными решением уравнения (2) методом половинного деления. Проверка проводилась для углов 0 ° <  ф <  20 ° , а точность совпадения была не хуже 10 ^{- 10}.

Решение уравнения движения в форме (1) методом разложения в ряд Тэйлора по параметру x = sin²( ф ) показало хорошее совпадение с результатами прямого интегрирования уравнения (1) (см. [5]) с относительной точностью не хуже 10 ^{- 8}.

В решении уравнения (1) (формулы (8)–(12)) не используется точное значение радиуса наибольшего отклонения электронов от внутреннего цилиндра ЦЗ r_m , а применяется r_{m 0} — радиус наибольшего отклонения электронов от внутреннего цилиндра ЦЗ для электронов без азимутальной компоненты скорости. Из этого, однако, не следует, что r_m вычислять не следует. Радиус r_m используется для сравнения с радиусом внешнего цилиндра r ₂ . Если для некоторой траектории r₂ >  r m , то такая траектория касается или пересекает верхний электрод ЦЗ. Т.е. эта траектория не проходит на детектор.