Об асимптотике уединённой внутренней волны в режиме волны разрежения

В данной работе рассматривается уравнение в частных производных вида.

D + ■   = _м е R,_t . 0                      (!)

с заданным начальным условием типа Римана

и(ж, 0) = по(ж),                                             (2)

где но (ж) — непрерывная вещественная функция вида н-, ж < ж- но(ж) = <

у (ж), ж- < ж < ж+,

ун+, ж > ж+ где н- < н+,ж- < ж+ — некоторые константы.

Ещё в середине 19 века были найдены примеры гладких функций Ғ (н) и но (ж), для которых решения н(х<Ь) задачи (1), (2) имеют разрывы, названные позднее в газовой динамике ударными волнами. В связи с этим возникает необходимость в определении обобщённого решения — такого решения н(ж, t) в классе обобщённых функций, для которого возможно было бы сформулировать и доказать его существование и единственность для задачи Коши (1), (2). Рассмотрим определение, приведённое в работе [1] для более общего случая систем, в рамках нашей системы (1), (2).

Определение. [1] Ограниченная измеримая функция н(ж,t) называется обобщённым решением задачи (1), (2) в слое n_t = R х [0,Т\, если:

1)Для любой константы к и любой гладкой финитной в n_t функции w(ж,t) > 0 выполняется неравенство

(|н — k|w_t + sign{u — к}[Ғ(н) — Ғ (к)]w_ж)dжdt > 0.

nt

• 2)    Существует такое множество Е нулевой меры на [0,Т\, что при t Е [0,Т] r Е функция н(ж,t) определена, почти всюду в R и что для любого множества Кр = {|ж| <  R} С R :

lim         |н(і, ж) — uо(ж^\dж = 0.

t^0,tE[0,T]rE J

Там же, в работе [1], доказывается для более общего случая теорема, о существовании и единственности подобного решения для соответствующей задачи Коши.

Возникает вопрос о поведении подобных решений н(ж, t) при t ^ то. Этот вопрос был решён Гельфандом в работе [2] для специальных начальных условий вида.

но(ж) =

{ и-, ж < жо н+,ж > жо,

где н- < н+ — некоторые константы.

Теорема. Гельфанда, впоследствии была, обобщена, в статье 1987 года. [3] для случая непрерывных монотонных начальных условий. Мы же приведём здесь недавний результат из статьи [4], обобщающий теорему для случая немонотонных начальных условий (такие условия могут встречаться в различных прикладных задачах, например, в математической физике или при моделировании шумпетеровской динамики распространения новых технологий (см. [5], [6])). Далее будем считать, что у(н) = Ғ (н).

Теорема. [4] Пусть ф(н) — непрерывно дифференцируемая функция, производная которой имеет только изолированные нули, и S = {н | Ғ **(н) <  Ғ (н)}, где будем считать, что S представимо в следующем виде: S = (н°_,н+) U (н-,н+) U ... U (н-,н+), где н- = н_-,н+ = н+, а такснсе dф(н±)/dн = 0, Z = 0, ...,L . Тогда решение задачи Коши имеет следующую асимптотическую структуру:

Н^Д) — н(^,t)||ы(кж) ^ 0, t ^ +то, н-, ж < со • t + dо

н(ж, t) = ^ 1 (ж/t), С/ • t + d/ < ж < С;+1 • t + dz+1,

I = 0,...,L — 1,

,н+,ж > cl • t + di где функция Ди) определена на дополнении к мноэюеству S , ci соответственно опреде лены по формулам

F(и¹₊) — Ғ (и—) и¹₊ — и—

I = 0,...,L,

a di могут быть определены из начальных условий с помоицъю правил Максвелла'.

di

] (ио(х)

У-

— и- ) dx +

у+

У (ио(х) di

— u^l₊)dx = 0,

где

ио(у1-) = и—, I = 1,...,L, ио(у+ )=ul+, I = 0,...,L — 1, ио(у—) = и-, ио(у+) = и+.

При этом функции у± определены следуюсцим образом;

Если и± / {и—,и+} или и± G {и—,и+} и dp(иl.t)/dи > 0, то ио (yL) = и—,  ио (у+) = и1+ х+ j (ио(х) — и—)dx у1

-

х+

= max / (ио(х) — и— )dx,

'У J

У х+

У (ио(х) — и^l+)dx у¹+

Если nice и± G {и_—,и+} 11 dp(и^l±)/dи <  0.

х+

■ - у.....^..  ........

то

ио (у— ) = и—,  ио (у+) = и+, у1у j (ио(х) — и—)dx = max j(ио(х) — и—)dx, X-X- у+у

У (ио(х) — иl+)dx = max j (ио(х) — иl+)dx. X-X-

Эта теорема показывает, что решение сходится к асимптотике по норме Li, причём асимптотика может быть получена из начальных условий, но остаётся вопрос о характере сходимости. Структура асимптотики — это чередование участков ударных волн и волн разряжения.

Для случая и_— > и+ и специальных начальных условий, отвечающих случаю одного участка ударной волны, в статье [7] доказано, что решение сходится к асимптотике за конечное время.

Теорема. [7] Пусти F(и) — выпуклая и пусти для началиного условия выполнено: ио(х) = и+ при х > N и ио(х) = и— при х < —N Д— > и+). а такэісс ио(х) — ограпииспа и измерима. Тогда До > 0 такое, что решение; и(х, t) задачи Коши при t > іо совпадает с u+ при х — kt — хд > 0 и с u— при х — kt — хд > 0, где к = ^(щ^тщ^-; a xq определено равенством

Х 0                 +^

J (ug(x) — u-)dx + j (ug(x) — u+ )dx = 0.

— ^                  X 0

Тем не менее в случае u_—< u+ сходимость за конечное время в общем случае отсутствует. Подобный эффект вызван внутренними ударными волнами, то есть ударными волнами, которые исчезают в асимптотике. Именно поэтому их изучение важно для разрешения вопроса о скорости сходимости к асимптотике в случае u_—< uy.

В недавней работе Петросян [8] получены верхние оценки на скорость сходимости: Пусть F(u) является дважды непрерывно дифференцированной и строго выпуклой. Предположим, что начальная функция uq(x) имеет односторонние предельные средние значения, не зависящие от смещения: Vag € R а+у

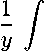
ug(x)dx ^ u_— щ>и у ^ —то равіюмеіию при а < ад, а а + у

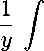
ug(x)dx ^ u+ щ>и у ^ +то равіюмеіию при а > ад.

а

Теорема. [8] Предполосисим, что Vag € R а+у

(ug(x) — u_—)dx = О(|у|^а-) п ри у ^—то, а

0 < а = coi 1st < 1. равномерно при а < ад, а+у

(ug(x) — u+)dx = О(у^а+ ) п ри у ^ +то,

а

0 <  а⁺ = coi 1st < 1. равномс'.рно при а > ад.

Пусть а = тах{а ,а ' }. u_ < uy. Тогда суні.ествует константа Т >  0. такая что

| u ( x, t) — u(x, t) | <  С • t ^{1+ 2-a} , C = coiist > 0

для t > Т и х € R. где- u(x,t) = H(x/t)

u_,x < pu—) • t

H (t) = p ¹ (x/t),p(u_—) < х/t < p(u+)

yu+, х > p(u+) • t.

Для начальных условий типа Римана мы можем считать, что величина а из теоремы выше стремится к —то, то есть верна оценка

V e >  0 ЗС = соnst > 0, ЗТ >  0 : | u ( x, t) — u(x, t) | < С • t ^1+е Vt > Т, V x € R.

В данной работе для специальных начальных условий типа Римана выводится результат о том, что существует нижняя оценка вида

З(С = со1 ist > 0, ЗТ> 0: |u(x,t) — S(x,t)| ><С • t—1, Vt > Т, Vx € R, то есть оценка из статьи Петросян для условий типа Римана не может быть улучшена в общем случае.

• 2.    Постановка задачи и основной результат

Рассмотрим уравнение (1) с начальным условием

п(ж, 0) = по(ж),

где Ғ(п) — равномерно выпуклая дважды непрерывно дифференцируемая функция, п-,ж < — N

G(ж),ж € [—N; 0]

пп (ж) =

J (ж), ж € [0; М ]

п+, ж > М, а п- и п+ — некоторые константы, п- < п+, G(ж) и J(ж) — строго монотонно возрастающие дифференцируемые функции, для которых G(0) > J(0), G(—N) = п-, J(М) = п+, M,N € R+- Таким образом, в начальный момент времени мы имеем разрыв в точке ж = 0. за эволюцией которого в дальнейшем хотим пронаблюдать. Известно, что для задачи (1),(3) новых разрывов появиться не может (это следует, например, из формулы Лакса-Олейник [9]), следовательно, только изначальный разрыв будет влиять на сходимость к асимптотике.

Сразу сделаем замечание, что замена координат позволяет привести любые подобные начальные условия с разрывом не в нуле к случаю выше, поэтому на самом деле положение разрыва в нуле не существенно и было выбрано нами для удобства рассуждений.

В каждый фиксированный момент времени t* мы можем рассматривать зависимость решения от координаты ж: п(ж, t*) может быть представлено в виде графика. Обозначим за hi(t) зависимость ординаты нижней точки разрыва от времени, а за Һ2 (t) зависимость ординаты верхней точки разрыва от времени. В этих обозначениях, h₂(0) = G(0), hi(0) = J(0). Обозначим R(t) = h₂(t) — h1(t).

Теорема 1. Для задачи Коши (1),(3) справедлива оценка R(t) > ^у, где С >  0 — некоторая константа, a R(t) определена више.

Доказательство

Пусть G*(h) = G^-1(ж). a J *(h) = J^-1(ж). Благодаря тому, что G и J — строго монотонно возрастающие функции, G* и J* существуют и также являются строго монотонно возрастающими. Получаем следующее уравнение, вытекающее из метода характеристик [9], смысл которого состоит в том, что в момент времени t характеристики точки на левом участке возрастания и разрыва пересекутся (справа записана характеристика точки на левом участке возрастания, а слева — характеристика разрыва):

G*(^2(t)) + Ғ‘ (^2(t)) • t = 0+ Г ^F h2 ' ^{F h} ' dT.

0      ^h2 ^{( t} ) ^— ^ 1 ^{( t} )

Аналогичное уравнение может быть записано для описания пересечения характеристик разрыва с характеристиками точек на правом участке возрастания.

Таким образом, получаем систему, неявно задающую hi(t) и h2(t):

(Ж(М+ + ^Ғ‘ (М+ • t = 0 + Jo‘ ^(T^SAwp^{1 d}T IJ -(hi(t)) + ^Ғ‘ (Mt)) • t = 0 + /„' ^{F ;} ' » ^dT.

Предложение 1. Для задачи (1),(3) функции hi(t) и h₂(t), введённые ранее, дифференцируемы по 1.

Данное предложение напрямую следует из формулы Лакса-Олейник.

. где

' е

Лемма 1. Для задачи (1),(3) справедлива оценка R(t)    >

С> 0, Е = min(F’’ (п) | п € [hi(0), h₂(0)]). к = max(F’’ (п) | п € [hi(0), h₂(0)]).

Доказательство

Продифференцируем систему (4) по t (мы имеем право это сделать, так как все функции, входящие в систему (4), дифференцируемы по своему аргументу на всей области определения) :

(G*^ (Һ2(t)) • h2(t) + Ғ' (h2(t)) + Ғ " M(t)) • h2(t) • t = ^F^^^ ,

^2(0) = G(0)

и ^ /л (

^2 (t) —^1 (t)

(j *)‘(hi(t)) • hi (t) + f' (Mt)) + F" (Mt)) • h^t) • t = _ч Д1(0) = J (0).

Выразим отсюда h^t) и hi (t):

h2(t) =

- F '(Ң + [ ^F ^Ь^¹) ]

(G*)' (h₂)+F " (h₂)-t ’

h2(0) = G(0),

h1(t) =

- F ' ( h i )+[ ^F^-F"¹) ]

( j *)' m+f " ( h₂>t ’

hi(0) = J (0).

Числитель правой части первого уравнения меньше нуля при любых Һ2 > hi в силу равномерной выпуклости F (п). Аналогично, числитель правой части второго уравнения больше нуля при любых Һ2 > hi. Так как функция F (п) равномерно выпукла, то можно оценить её вторую производную на участке [hi (0); h₂(0)] как 0 < е < е <  F (п) < к < +то. Из монотонного возрастания функций G* и J* и того факта, что t >  0, следует, что оба знаменателя являются положительными, то есть Һ2Д) < 0 Vt > 0 , a М (t) > 0 Vt > 0. Тогда мы можем записать следующую оценку:

h2(t) >	- F '(M+[ f ( " 22)- F 1 ( " 1) ] e ^ t
h2(0) =	G(0),
hi(t)<	- F ' ^ iM F F^_ e ^ t	-F("1) ] - "1       -1

4hi(0) = J (0).

Вычитая из первого неравенства системы второе, получаем следующую оценку:

I

R' (t) >

F '(M-F W e-t

R(0) = G(0) - J(0) > 0,

> F‘(hi) - Ғ‘(Һ2) = F " (Д • -R(t) > к • -R(t) ^_ е • t             е t ^— е t

Покажем, что из этого следует оценка х х const

R(t) > R(1) • ——.

Будем действовать в духе доказательства леммы Гронуолла:

R' (t) > ^К •^й . е t

Перенося всё в левую часть и домножая на эксопненту, являющуюся положительной величиной, получаем

R' (t) • exp Q^ Мт ) + R(t) • -j- • exp Q Mt ) > 0.

Заметим, что выражение справа может быть переписано в виде dt R^ (і dr)) > 0.

Отсюда получем следующее утверждение:

. const С R(t) > R(1) •       =    , что и требовалось доказать.

Таким образом, при любом конечном Т > 0 можем считать, что R(T) > 0 — некоторое число.

Тогда будем рассматривать е(Т)   = min(F (n) | n G [h1(T),h2(T)]) и к(Т) = max(F (n) | n G [Ді(T),h2(T)]). Так как производная hi по времени больше нуля, а производная h2 по времени меньше нуля, то [hi(Т),ҺДТ)] постоянно сжимается с двух сторон с ростом Т, из чего следует, что если Һ2(Т) ^ ҺДТ) при Т ^ +то, то и к(Т) ^ е(Т) при Т ^ +то.

Предложение 2. Для задачи (1),(3) справедлива оценка R(t) < —^—, где ’                           t '-      ’

С > 0, е  = min(F (n) | n G  [h₁(0), h₂(0)]), к =  max(F (n)  | n G  [h₁(0), h₂(0)]).

При этом  h₂(t) ^ h₁(t) пр и t ^ +то и «(t) ^ e(t)  п ри t  ^ +то, где

«(t) = max(F (n) | n G [h₁(t), h₂(t)]) и e(t) = min(F (n) | n G [h₁(t), h₂(t)]).

Это предложение непосредственно следует из результата Петросян, приведённого ранее.

Покажем, что всегда можно уточнить оценку снизу, рассматривая поведение системы не в начальный момент времени, а в момент времени Т:

/R‘(t) >

(R(0) = G(0) - J(0) > 0,

‘       F‘(h1) - F‘(Һ2) ₌ F t   -Rt)     «(t) -R(t)

R (t) >       е(Т) • t           e(t)        t > e(t)t ’

Будем действовать аналогично предыдущему доказательству для нижней оценки:

R' (t) > «| • R, откуда получаем f t K(t)    \              K(t)          / t K(t)\

^)dr + R(t) • ^) - exp     ^)dr > 0,

J T r I             ^-         \ J T r I откуда в свою очередь d_ dt

> 0, из чего следует, что

(г t^ ^l  \            t _ft     \

R(t) > R(T) • exp I —    -^)dr I > R(T) • exp I —    -^^(T)-dr I = R(T) • _{k ( t} , .

\   7 t ^r    I                \   7 T   ^r i            t Ft)

Так как мы знаем, что к(Т) ^ е(Т ) при Т ^ +то, то есть ^^т) ^ 1 пр и Т ^ +то, то остаётся вопрос о том, сходится ли -R- к 1 при Т ^ +то.

t "=7 < 7

Запишем разность в виде дроби:

«(*) t^e(t)

-

1 = 1 t

-

«^(t) _-1 t^e(t)

иМ te(t)

.

Можно утверждать, что существует сходимость -H(ty к 1 при t ^ +то, если ограничен t "=№ числитель данной дроби. Числитель ограничен тогда и только тогда, когда ограничен его логарифм:

""(t) — 1^ • b(t) < const.

Для доказательства сходимости нам необходимо доказать справедливость утверждения выше.

Вспомним, что "(t) и 6(t) — это максимум и минимум на отрезке [^i(t); ^2(t)] непрерывной функции F (и). Тогда, об означая за А максимум производной F (и) на отрезке [Һ1 (0); ^2(0)], получаем следующую оценку:

"(t)

-

6(t)

Отсюда, зная верхнюю оценку для

₌ "^{(t) — 6(t)}

6(t)     "

R(t) • А

′

.

R(t), получаем, что

"^(t) _— 1

6(t)

≤

R(t) • А

′

≤

const• А

Из этого при t ^ +то следует оценка вида |(7й

—1

≤

что -^ ^ ¹ щ^{)П т} ^ ^х t ^e(t)

Таким образом, мы показали, что для системы оценка: R(t) >  ^А. Теорема доказана.

′

R ( t\A

′

€

(1),(3)

·

e .

t ' -

— Tnfty- Таким образом получаем,

справедлива следующая нижняя

Замечание 1. Учитывая, что мы показали, что координата верхней границы разрыва со временем уменьшается, а нижней — увеличивается, можно ослабить требования на F (и), потребовав строгую выпуклость лишь на [Н (0) ,G (0)].

Замечание 2.: Данная оценка очевидно может быть перенесена на класс начальных условий, которые за конечное время приходят к виду (3). Более того, существуют начальные условия, при которых скорость сходимости верхней и нижней границ разрыва имеет вид ^опвф то есть оценка не может быть улучшена для общего случая начальных условий вида (2). Пример таких начальных условий для F (и) = и²:

ио (ж) = <

— 1, ж < —1, 5,

3 ж + 1, ж е [— 1, 5; 0], 3ж — 1, ж е [0; 1, 5], 1, ж > 1, 5.

Как несложно получить, к примеру с помощью задачи Коши (1),(5) будет

формулы Лакса-Олейник, решением

—1, ж

< —1, 5 —

и(ж, t) = <

4ж+3

3+8 t , ^{ж е [} 1, ⁵

2t,

— 2t;0],

43+ - I ,ж е [0;1, 5 + 2t], 1,ж > 1, 5 + 2t.

В данном случае при каждом фиксированном t при ж = 0 решение будет иметь разрыв, размер которого зависит от t как R(t) = 3+87 •

Работа выполнена при финансовой поддержке РФФИ (проект 20-07-00285).