Об интегральном представлении типа Меллина-Барнса решения системы полиномиальных уравнений специального вида

Введение. Интегралы Меллина-Барнса являются обратными преобразованиями Меллина для отношений произведений конечного числа гамма-функций в композициях с линейными функциями. Частные случаи этих интегралов впервые появились в работах Б. Римана, связанных с теорией гипергеометрических функций. Позднее Х. Меллин развил их теорию [1], а Е. Барнс разработал метод получения асимптотических разложений для разных классов функций, определяемых степенными рядами и интегралами [2]. Отдельно следует подчеркнуть роль интегралов Меллина-Барнса в теории алгебраических уравнений. Впервые такое их применение было продемонстрировано Х. Меллином в работе 1921 года [3], где были найдены интегральные формулы для решения общего алгебраического уравнения. Интегральную формулу и неполную область сходимости Меллин привел без доказательства. Полное доказательство этой формулы с указанием истинной области сходимости было предъявлено И. А. Антиповой [4].

Проблема сходимости интегралов Меллина-Барнса привлекала внимание специалистов на протяжении последнего столетия. В одномерном случае вопрос о сходимости был решен в серии статей и монографий: А. Диксон и Б. Феррар [5], Л. Слейтер [6], Г. Бейтмен и А. Эрдейи [7]. Шаги к решению этой проблемы в многомерном случае были сделаны Х. Меллином, Р. Бушманом и Х. Сриваставой [8], О. Н. Ждановым и А. К. Цихом [9]. Окончательно область сходимости многомерного интеграла Меллина-Барнса найдена М. Пассаре, А. Цихом и Л. Нильсон [10].

Представляет интерес задача исследования сходимости интегралов Меллина-Барнса в граничных точках их областей сходимости. Для интеграла Меллина-Барнса, представляющего решения алгебраических уравнений, эта задача рассмотрена в работах [11; 12]. Интегральные преобразования Меллина для решения общей системы алгебраических уравнений исследовались в ряде современных работ [13; 14], в которых прямое преобразование было вычислено с помощью линеаризации системы (замены переменной специального вида). В данной работе исследовано множество сходимости интеграла Меллина-Барнса, представляющего решение полиномиальной системы уравнений специального вида.

Преобразование Меллина мономиальной функции решения общей полиномиальной системы. Рассмотрим приведенную систему n полиномиальных уравнений:

y mi + 2 X Л‘) У ' — 1 = 0, i = 1, - , П (1) л \('^:

с неизвестными у = ( y 1 , ..., y_n ) е Tⁿ и переменными коэффициентами x Л¹) , где Л ⁽¹) с X ” - фиксирован- λλ λ ные конечные   подмножества;    у = У 1¹ — У п^п ;

mi еX+;    г = 1, ..., n.    Обозначим через Л дизъюнктное объединение множеств Л( 1), и пусть N = #Л - число коэффициентов в системе (1). Множество коэффициентов этой системы пробегает векторное пространство CЛ = Cx, в котором координаты точек x = (xЛ1)) индексируются элементами Л е Л. В работе [15] для мономиальной функции

у ^{Г ( - x} )" у Г* ( - X ) — у Г ⁿ ( - X )’

Г>0,      (2)

составленной из координат У j (- x ) решения системы уравнений (1), было вычислено прямое преобразование Меллина, определяемое интегралом

M

У ^ц ( — x )

( z )= I" —-— x z I dx , K N У "  (^- x )

где x z I = x z ^{1 1} — x N 1 , dx = dx 1 — dx_N

Множество сходимости интеграла, представляющего функцию вектор-решения полиномиальной системы уравнений специального вида. Рассмотрим приведенную систему двух полиномиальных уравнений вида

У™1^ xyл(°-1 = 0, 1 = 1, 2,(4)

Ф =

с двумя переменными коэффициентами x 1 , x ₂ . Обозначим через А определитель матрицы

" Л(1) - m1 л ч Л21)      Л(22) - m2

и предположим, что А >0. Введем векторы хр ^ = ( Лр ¹ , m 1 - Л ⁽¹⁾ ) , хр ₂ = ( m ₂ - Л^ , Л 21) ) , ортогональные вектор-строкам матрицы Ф .

Теорема. Мономиальная функция —-—, состав У ^Г ( - x )

ленная из координат решения системы (4), представляется следующим интегралом Меллина-Барнса:

1 2

1 П (2п 1 ) 2 /=1 ^{v 7} Y+ 1' К^{2 1 1}

I + ( *, z >)г ( z^ ( m m

ГI + ±( *, z > + 1 ( m m

х Q (z1, z 2) x1 z1 x 2 z2 dz1 dz 2, где полином

Q ^{( z} 1, ^z 2)=^— ^{х m} 1 m 2

• ^х ( Г 1 Г 2 ⁺ Г 1^Л2) ^z 1 ⁺ Г 2^Л1²⁾ z 2 ^{-A z} 1 z 2 ) ,

а вектор у е К ² выбирается из открытого множества

U = { и е К + : г + (* ₁ , и > > 0, 1 = 1, 2 } .        (6)

Множество сходимости интеграла (5) в переменных 0 = arg x определяется неравенствами

Iон;П ( m - - ^Л-’ ) • К* ■ •⁰) 1<;П^{А ,} " ¹ - ² - ⁽⁷⁾

Доказательство. Идея доказательства представления мономиальной функции —-— интегралом (5) У ^{р ( -} x )

в секториальной области, определяемой неравенствами (7), заимствована в работе [4], поэтому первая часть доказательства излагается кратко.

1. Для простоты положим р 1 = р ₂ = 1. Начнем с описания секториальной области голоморфности функции

У (-x(,)) = У1 (-x (S)) У2 (-x(,)),          (8)

где зависимость x (,) = ( X i (^ i ,, 2 ), x 2^,^ 2 ) ) определена заменой переменных (линеаризацией) в системе 1

Кроме того, функция y ( - x ) голоморфно продолжается в область S Po = x ( S _т ‘ ) - образ секториальной области S _т ' с С 2 при отображении x (,). Область S Po есть секториальная область над внутренностью выпуклого многоугольника P следующего вида

P =

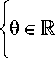
К ♦"• 6)1

- ( т. - X ( ¹ ) ) , m_i

I

< — X , i = 1, 2 k ^m.

[15], причем ветви радикалов W™^j выбраны условием их положительности при , е R 2. . Рассмотрим 1

функцию У( ( - x ( , ) ) = ( 1 + , i ) mi . Она голоморфна (как многозначная функция) вне прямой L i = { , е T ² :1 + , . =0 } , где T ² = ( С \ { 0 } ) ² . Более того, функция y i ( - x (,) ) голоморфна (и однозначна) в секториальной области S _т i над выпуклым множеством т i = { те К² :| т i | < п } , где т i = arg, i , i = 1, 2.

Следовательно, функция (8) голоморфна и однозначна в секториальной области S _т над множеством т = { т е К ² :| т i | < п, i = 1, 2 } . Заметим, что якобиан

„    d( x )

Итак, поскольку якобиан д^) не обращается

в нуль в S _т ' , x (,) отображает S _т ‘ на S Po локально биголоморфно. Тем самым для x = x (,) е S Po функция y ( - x ), будучи представленной как

П(1 + ,j)mj       , является голоморфной. В силу j                  ,=,-*( x)

односвязности S Po она голоморфна, следовательно,

голоморфна функция

1 y ^{( - x} ).

Для доказательства представления мономиальной

d ( x )

д^у линеаризации (в случае n = N = 2) обращается

в нуль на множестве

функции ----- интегралом (8) нам необходимо

y ^{( - x} )

констатировать еще одно ее важное свойство:

на множестве S Po она удовлетворяет условию

^V , =

< , е T ² :1 +

т 1 - X ^{(1) m} 1

,1 +

1 y ^{( - x} )

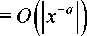
для всех а е U 1 , где U 1 - открытое

+

т ₂ - X ₂ ²⁾

^т - 2

А

, 2 +----- , 1^2 =0

1 ^m

(см. [15]). Оно при такой замене переходит в множество ветвления алгебраической функции y ( - x ), т. е.

дискриминантное множество V системы уравнений (4). Полином переменных , 1 , ,₂, определяющий нулевое

множество якобиана V , , имеет положительные

коэффициенты у всех мономов, поэтому существует выпуклое множество т' с т с К ² , 0 е т ' , такое, что в секториальной области S _т‘ над каждой точкой те т'

множество (6) при р 1 = р₂ =1.

Таким образом, применяя формулу обращения для многомерного преобразования Меллина (см. [4]), 1

получаем представление функции ----- в виде

y ^{( - x} )

интеграла Меллина-Барнса вида (5) в секториальной области S .

Po

2. Исследуем интеграл (5) на сходимость в граничных точках области S Po . Идея доказательства подробно изложена в работе [12]. Можно оценить модуль подынтегральной функции в (5) при | и Ч да

расположен ортант е^{1 т} К + = { , = ( r_x е^{1 т}1 , r ₂ e^{1 т}2

h>° j ,

выражением вида

свободный от точек V , .

Функции ( 1 + , i ) mi , i = 1, 2, допускают выделение ветвей (со значением 1 при , i =0) в секториальной области S _т. Следовательно, таким же свойством обладает отображение x (,) и функция (8).

2 п j =1

( ^{| и} j ^{1 + 1} ) ^{n j} (I j , ^и)| ⁺ 1 ) , ^j

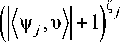
2 (

^X exp j (^u,9)^{- п} ^ ^{1 u} j ¹ + ² j =1 1

I <^j, u)| mj

Q ( u ,и) X

I < V j , u ) |

где     Q ( и , u) = Q ( z )|,

а

показатели степеней

не смогут «погасить» рост экспоненциального

определяются следующими

формулами: n j = U j

^^^^^^в

2,

множителя.

Пусть 9 е д P . Если матрица V , составленная из

,      1             0 j

^j =—\V j, u)+-- mjmj

w

μ j

m

2,

Z j =

μ j

mj

2,

показателей системы (4), не содержит нулевых

элементов, то Р представляет собой восьмиугольник на рис. 1. Вершины восьмиугольника Р имеют коор

j = 1, 2.

Из вида выражения (9)

следует, что сходимость

динаты K 1 1 - п

интеграла (5) контролирует показатель экспоненты

- Х<0 m, - X® --—, п 2--— m1        m 2

K 2

mx - X(1) п —--— m1

П .I

^{U K} °) -^ । ^U j । ^{+ 2} j =1 1

I (ФрУ> I I J,y> I ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^B  ^^^^^^B  ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^B

m

m

,

m ₂ - X 2²⁾ 1 Л   X 2°   m ₂ - X® ) Г   X? ’

--------- ,   K ₃ ^{- п}---- ,^п--------- , K ₄ ^-п----, m ₂     J I m ₂ m ₂ J I     m ₂

степенной множитель

2 п j =1

ξ j

m2 - X22’ п------- m 2

I Jm K 5 ^п

- X (1’        1 Д m - xP’

-----,^{- п}      , K 6 ^-п-------- m 1         m 2 J I       m 1

ζ j

,

а также функция Q ( и , и), отличная от константы в

X ⁽²⁾ 1 п ¹ , m 2 J

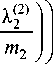
случае интеграла, представляющего решение системы уравнений.

Если при фиксированном 9 = (9 1 ,9₂) е К ² показатель экспоненты (10), зависящий от и = (и 1 ,и₂) е К ² , есть величина отрицательная, то экспоненциальный множитель (9) убывает и степенной множитель (11), и функция Q ( и , и) не могут нарушить сходимость интеграла. Эта ситуация будет иметь место при 9 е P ^o . Напротив, неограниченное возрастание показателя экспоненты (10) для какого-либо направления и = (и 1 , и₂) говорит о том, что для выбранного 9 = (9 1 ,9₂) интеграл будет расходиться, так как степенной множитель (11) и функция Q ( и , и)

стороны будем обозначать [KiKj ]. Множество точек относи тельной внутренности стороны [KiKj ] будем обозначать (KiKj).

Он может вырождаться в шестиугольник, если один из показателей X21’ или X(2’ равен нулю. Если X0’= X(2’= 0, то система (4) распадается на два уравнения, и эту ситуацию мы не рассматриваем. Проведем доказательство для случая, когда Р -восьмиугольник. В других случаях оно будет аналогичным.

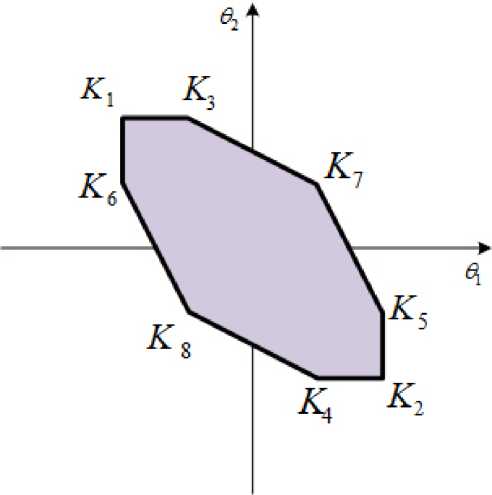
Рис. 1. Восьмиугольник Р

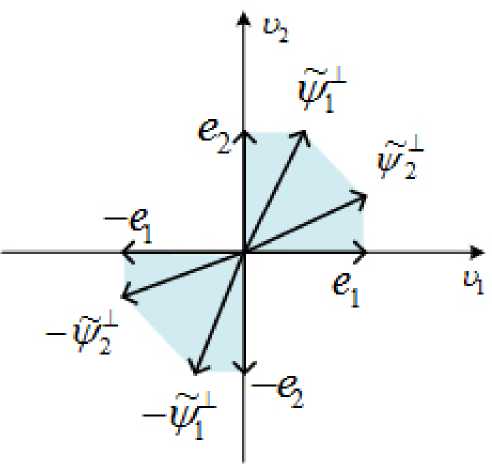
Рис. 2. Множество X

Как отмечалось ранее, поведение подынтегральной функции в (5) во многом зависит от размерности множества направлений и, на которых показатель экспоненты в оценке (9) обращается в нуль при фиксированном 6 . Объединение таких множеств по всем 6 ед P обозначим 2 . Это множество состоит из одномерных конусов о ± ( e i ) := { re i е R ², r > о } , о ± (/^X):= { п / ^X е R ², r > о } , j = 1, 2 и двумерных конусов

+ X              X 2

^о2 ^{( e} 1 , У 2 ^): = { r l e l ^{+ Г} 2 ^ 2 ^{е R} , r j > ⁰ } ,

О± (ФX , e2):= { rXX + r2e2 е R2 , rj > 0} , о±ОФX, VX):= {ri'/X+ r2VX е R2, rj> 0}.

Для случая, когда Р - восьмиугольник, множество 2 изображено на рис. 2. Если 6 е (K1K3), то показатель экспоненты (l0) обращается в нуль для всех и е о+ (e2) (и только для них). Для стороны (K1K6) соответствующим множеством зануления будет одномерный конус о-(e1). Для наклонных сторон (K3K7), (K7K5) показатель экспоненты (10) обращается в нуль в одномерных конусах о+ (х/ ) и о+ (х/2 ) соответствен- с     о f mi —Z(1) m2 — Z°2) 1 г но. Если 6 = -п —1---—, п —---— (вершина K1), I       m1          m 2   J показатель экспоненты (10) обращается в нуль для всех и е о+ (e2) и о- (e1). Для вершин K3, K7, K5 такими конусами будут двумерные конусы о+ (х/X, e2), о 2 (L, / 2),    о+ (e1, / 2) соответственно. Для остальных сторон и вершин восьмиугольника картина будет симметричной (см. рис. 1, 2).

Требует детального исследования поведение интеграла (5) в окрестностях направлений и = (и ₁ , и ₂ ), на которых (10) обращается в нуль.

Рассмотрим сторону [ K ₃ K ₇] восьмиугольника P . Для других сторон рассуждения будут аналогичны. Зафиксируем точку 6 = (6 ₁ ,6 ₂ ) е ( K ₃ K ₇ ). Конус о + (V ^X ) является гранью двумерного конуса о 2 (/ , e ₂). Показатель экспоненты (10) для направлений и из конуса о + (хр ₁¹, e ₂) примет вид

const JJ о+ <’1'1,e 2)

^(и1 + ^{1)П1 (и}2 + ^1)П2

**

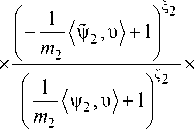
х Q ( и , и) exp <  I 6₂

m п—

Л 1

^m 2

(/₁,и) Г d и₁ d и₂. (12)

Справедлива следующая лемма.

Лемма. Интеграл (12) расходится.

Доказательство леммы. В интеграле (12) сделаем замену переменных:

U 1 = Ю 1 ,

( V 1 ,^и) = ® 2

якобиан которой равен ненулевой константе. В результате такой замены интеграл (12) примет вид

N ^²

где

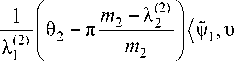
1 Га    m -' La а I Г.

причем — 62 -п ——— <0 для 62 е п 1—1— , лу1 |        m2 J ||   m1 m2 J

_ m2 - Х2) 1_ п------- . С учетом оценки (9) исследование m 2 J интеграла (5), при фиксированном 6 е (K3 K 7), сводится к исследованию сходимости следующего интеграла:

J

^R +

V ^Z1 R ^Z2

х

x Q ₁ ( и , ю) exp < I 6

m п —

^m 2

х ⁽²) 2

-^— I ю ₂ Г d ю ₁ d ю ₂ ,

L (ю) = ю ₁ + 1, V (ю) = ^ 2- + ю ₁ + 1, m ₁

M (ю)^ ( - (L ) /^{(2) х}

- m 1 )to 1 ) + 1,

N (ю) = ^рт (А Ю 1 - (Х 2^{2) m} 2 ^ ⁽ )

^{- m} 2^)ю2 ) ^{+ 1} ,

^{R (Ю)} = 7(2)" ( ( m 1 m 2 - ^Xl¹⁾ m 2 ^-А ) ^Ю1 ^{+ Х}2²⁾ ™ 2 ) ^{+ 1} , m 2 ^ 1

C Q 1 ^{( и} , ^ю) = Q 2 ^{( и}1 , ^и 2 , ^ю1,----VTTT ^(ю2 ^- М^{2) )ю}1 ).

m ₁ - л ()

Представим интеграл (14) в виде повторного:

”       Гал    X¹

J I ( ^ю2 ) I — ^{+ 1} I

0       2 ^m 1    I

exp 2 1 6 2

- п

m 2 - ^ 2^{2) m} m 2

ю₂ Г d ю₂, (15)

где

X

I ^{( Ю}2 ) = J 0

L ⁿ¹ M ^П2 N ^Z2

V ^Z1 R ^Z2

Q ₁( и , ю) d ю₁.

Исследуем сходимость интеграла (16). Степень подынтегральной функции по переменной ю1 в (16) равна

Ё( П- Z7) + ^2

j =1

+ 2 = - 3

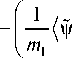
m ₁

+ 2 =

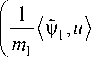
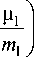
Здесь выражение в скобках больше нуля в силу условий (6). Степенной множитель Q 1 ( u , ω) дает существенный вклад (слагаемое, равное 2) в сумму (17), так как degQ ( z 1 , z ₂) = 2 при условии A >0. Из неравенств (17) следует, что интеграл (16) расходится. Как следствие, расходится и интеграл (15). Лемма доказана.

Исследуем вершины восьмиугольника Р . Точке K 1 соответствуют в множестве 2 два одномерных конусах о + ( e ₂) и о - ( e 1 ). Поэтому, чтобы констатировать расходимость интеграла (5) в точке K 1 , необходимо и достаточно исследовать эту точку в составе сторон [ K 1 K 3 ] и [ K 1 K 6 ]. Аналогичным свойством обладает симметричная точка K 2 .

Прообразы вершин K 3 , K 7 , K 5 , K 4 , K 8 , K 6 восьмиугольника P также не входят в множество сходимости интеграла (5). Действительно, в этих точках зануление показателя экспоненты (10) происходит по всем направлениям υ = (υ 1 , υ 2 ), принадлежащим двумерным конусам, которые были перечислены выше. Поэтому задача сводится к исследованию сходимости двойных интегралов от степенных функций по этим конусам. Эти интегралы расходятся, так как степенной множитель (11) и функция Q ( u , υ) имеют суммарную степень по переменным υ 1 , υ 2 , равную –1.

Итак, мы можем сделать вывод: множество сходимости интеграла (5) есть секториальная область S Po , основание которой определяется неравенствами (7). Таким образом, теорема доказана.

Заключение. В данной работе получено интегральное представление типа Меллина–Барнса мономиальной функции вектор-решения системы полиномиальных уравнений специального вида с указанием множества сходимости.

Acknowledgments. This work was supported by the Russian Foundation for Basic Research № 15-31-20008-mol_a_ved, 14-01-00283-a.