Об инвариантах структуры серий и критериях случайности последовательной выборки

Самарский государственный аэрокосмический университет

В статье рассмотрены закономерности формирования серий, образуемых в последовательной выборке непрерывной случайной величины положениями индивидуальных значений относительно центральной линии (медианы) и отношениями порядка между соседними значениями. Показана возможность обобщения результатов теории рекуррентных событий Мизеса-Феллера для серий, образуемых отношениями порядка. Получен общий вид производящей функции времени возвращения и асимптотические оценки числовых характеристик числа серий фиксированной длины для серий указанного типа. На основании установленных законов распределения выявлены инварианты структуры серий, сформулированы критерии случайности выборки и проведена их экспериментальная проверка путем статистического моделирования методом Монте-Карло.

Одним из основных исходных понятий в приложениях теории вероятностей является понятие случайная выборка (из генеральной совокупности). При этом категория случайности, строго определяемая, как равновероятность попадания в выборку каждого из значений генеральной совокупности при постоянстве последней, зачастую интерпретируется, как отсутствие какой бы то ни было закономерности в последовательности выборочных значений, то есть как хаотичная последовательность. Однако это не совсем так и при ближайшем рассмотрении случайность, а именно, равновероятность, обнаруживает признаки закономерности вполне детерминированного характера.

Одним из проявлений закономерностей в случайной последовательности является образование в ней по мере возрастания длины характерных структур (структурных инвариантов), которые представляются интересными с точки зрения возможных приложений и могут служить критериями случайности.

Известными элементами таких структур являются инверсии, циклы и серии [1,2].

В [3] был рассмотрен закон распределения длины максимальной серии. Далее речь пойдет о некоторых результатах, касающихся более детальной структуры серий. Прежде видимо следует в двух словах повторить преобразования, позволяющие установить связь между последовательной выборкой и классической теорией серий.

Рассмотрим последовательную выборку непрерывной случайной величины (С.В.). Для каждого выборочного значения очевидно существуют два и только два равновозможных и взаимоисключающих положения относительно медианы ((>>//<<)). Причем, положения всех значений (точек) независимы в совокупности, следовательно, закон их чередования идентичен закону чередования исходов опытов с симметричной монетой.

Для каждой пары соседних точек существуют также два равновозможных отношения порядка (два знака последовательной разности). Однако последовательные разности (П.Р.) уже не являются независимыми. Любые две соседние П.Р. коррелированы с коэффицентом rr=- 2 [[4]]. Применительно к опытам с монетой можно представить дело таким образом, что монета “запоминает” пре-

дидущий исход и с вероятностью 3 воспро- изводит его в следующем опыте. Соответ- ственно с вероятностью 3 реализуется аль- тернативный результат [3,4].

Серией в двоичной последовательности, однозначно определяемой исходной выборкой, является группа последовательных то- чек одного знака. Причем, следуя В. Феллеру [[11]], определим серию, как рекуррентное событие. Например, отрезок последовательности …0111110… одновременно содержит 5 серий “1” (успехов) длиной 1, 2 серии длиной 2 и по 1-ой серии длиной 3,4 и 5. Такое определение серий позволяет использовать аналитический аппарат теории рекуррентных событий, являющейся , в свою очередь, частным случаем теории восстановления [1].

Серии положений точек относительно медианы являются сериями успехов в последовательности испытаний Бернулли с веро- зоваться аппаратом производящих функций.

Пусть u_n ^{( l )} – вероятность того, что на шаге с номером n образуется очередная серия длиной l . Тогда для u_n ^{( l )} справедливо рекуррентное соотношение [1] :

( ¹ ) „_м( ¹ ) _d²_u( ¹ )            l ^{- 1} -М ¹ )

u n ⁺ pu n - 1 ⁺ p u n-2 ⁺ ... ⁺ p u n - l + 1 ^- p ,

( l )            ( l )        ( l )                ( l )                               (1)

u о      j. , u 1       u 2       ... U | 1 v)

Умножая первое соотношение (1) на s ^k и суммируя по всем к >  l , получаем производящую функцию последовательности u_n ^{( l )} :

ятностью успеха p - — ,

для которых в лите-

U ( s ) -

1 - s + (1 - p ) p's^{1 + 1} (1 - s )(1 - pV )

ратуре имеется исчерпывающие или почти исчерпывающие результаты (относительно рассматриваемой задачи). Их краткое изложение ниже приведено исключительно с целью сокращения последующих выкладок, касающихся серий отношений порядка, путем рассуждения по аналогии там, где это представится возможным.

Рассмотрим последовательность исходов испытаний Бернулли и введем в рассмотрение целочисленные С.В. T_l – длину последовательности, при которой образуется первая серия успехов длиной l – время возвращения серии длины l и R_n ^{( l )} – число серий длины l в последовательности длиной n >  l . Как показано в [1] , серия успехов длины l является достоверным рекуррентным событием с конечным средним временем возвращения µ_T =М[[ T_l ]] и конечной дисперсией σ_T ² =D[[ T_l ]]. Для числа серий при больших n , как гласит теорема Мизеса-Феллера[1], справедлива асимптотическая нормальная оценка:

Переходя к производящей функции хвостов времени возвращения, используя соотно-

шение

Q l ( s ) -

(1 - s U , ( s )

[11], получаем :

R n ^{( l )} ~ N ( ⁿ , σ T_l µ T_l

n ₎

^µ T ³ l    ^.

Таким образом, задача установления закона распределения числа серий R_n ^{( l )} сводится к отысканию числовых характеристик времени возвращения T_l . Для вычисления числовых характеристик удобнее всего восполь-

~ A       1 - ps^l

Ql ^{( s} )^- -------- 7.-----_x . .         (3)

1 - s + (1 - p ) p s ^{1 v} ’

Числовые характеристики времени возвращения находим используя свойство фун- кции Q (s) и полагая p - 2:

Pt - Q l (1) - 2 ^{l + 1} - 2,

^ T - 2 Q l (1) + Q l (1) - Q l ² (1) - 2^{2( l + 1)} - (2 1 + 1)2 ^{l + 1} - 2 .

Далее, на основании теоремы Мизеса – Феллера получаем числовые характеристики числа серий успехов длины l :

_{n          2}     nσ_{T l}

^P R"^l ) ~"u" ,     ^R n ^l ) * ""^. (⁵⁾

µ T l                  µ T l

Для больших l очевидна асимптотическая оценка:

2 n

^P R ( ^l ) * ^ R n, ^l ) * 2 1 + 1      .           ⁽⁶⁾

Таким образом число длинных серий успехов имеет Пуассоновское распределение

(l)      n с параметром ^n - 27+r.

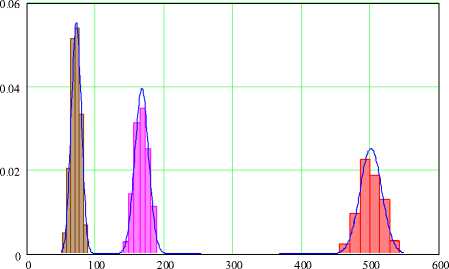
Рис. 1. Распределение числа серий успехов в выборке объема n=1000 в зависимости от длины серии ( l = 1 ^ 3 )

Общая формула для элемента такой

матрицы имеет вид: a ln

n l

. Определи-

тель А равен 1, следовательно существует А ^-1 . При этом среднее значение числа естественных серий можно вычислить и без решения системы уравнений. Они состав-

ляют

n

^Ц ~ ( ) = 2 7 + 2

Дисперсии

пред-

ставляют собой взвешенные суммы:

На рис. 1 представлены результаты статистического моделирования. Гистограммы числа серий для значений l = 1 ^ 3 (в порядке убывания средних) построены по 200 реализациям нормальной выборки объема n = 1000. Сглаживающие кривые представляют собой функции Гаусса с числовыми характеристиками, вычисленными в соответствии с (5).

Средние и дисперсии числа серий первого типа приведены в табл. 1.

Зная закон распределения числа рекуррентных (Феллеровых) серий, можно установить закон распределения “естественных” серий фиксированной длины R ^~ _n ^{( l )} , то есть когда короткие серии поглощаются покрывающей их более длинной серией. Так, в ранее рассмотренном примере будет содержаться только одна серия успехов длиной l = 5.

Числа рекуррентных серий связаны с числами естественных серий системой линейных уравнений c матрицей следующего вида:

	Г 1	2	3	4.
	0	1	1	2.
A =	0	0	1	1.
	0 ....	0	0	1.

2 _ V    - 1 ² 2

°Rnl) = ^ (ak ) ^rk) , где k=l ak 1 - элементы

матрицы А ^-1 . Отсюда следует, что числа рекуррентных серий обладают минимальными дисперсиями, стало быть, критерии, построенные на законах их распределения обладают большей эффективностью. То же самое справедливо и для суммарного числа серий успехов и неудач фиксированной длины.

Производящую функцию времени возвращения трендовой серии найдем по аналогии. Пусть, как и раньше, un(l) – вероятность образования на шаге с номером n очередной восходящей серии длиной l. В пространстве П.Р. соответственно образуется рекуррентная серия успехов (“1”) с параметрами: n* = n -1, l' = I -1. Как было показано в [33], вероятности серий в пространстве П.Р. инвариантны по отношению к закону распределения совокупности и определяются с помо- щью собственных функций:

u nl ) = J ф \ l ^{) ( x} ) d^x .

Для последних справедливы рекуррентные соотношения, аналогичные (1). Отличие заключается в том, что порядок рекуррентного соотношения на единицу меньше, а ум-

Таблица 1. Среднее значение и дисперсия числа серий в зависимости от длины серии

l 1 2 3 4 5 6 > 7 µ n 0,5 0,167 0,071 0,033 0,016 0,008 1 2 l+1 σ2 n 0,25 0,102 0,052 0,027 0,014 0,007 1 2 l+1 ножению на вероятность успеха p соответ- ствует операция j * dx. Например, для I =2:5 0

рекуррентные соотношения имеют вид:

тП2) (x) = x, x1

т П3 ⁽ x ) + J т П - ⁽ x ) dx = 7 x ² , 0 2

(4) x (4)              x x (4)               1

T n  ⁽ x ) + j T n - 1 ⁽ x ) dx + jj ^ n - 2 ⁽ x ) dx д x ,

0             00

x           xxxxx тП5’(x)+j тП-(x) dx+j j тП-)2(x) dx+j j j тП-з(x) dx =—x4.

0                 0 0                  0 0 0

В общем виде, при произвольном l , рекуррентное соотношение выглядит следующим образом:

тП1)(x)+ jтП-1(x)dx+...+ jjтП-i+2(x)dx = 7x77, , 0                         0     0                      (11)!

т 1¹ )⁽ x ) ^{s 1} , т 2 ¹ )⁽ x ) = ... = тУ )⁽ x ) = 0 .

По аналогии с сериями успехов в последовательных испытаниях Бернулли, производящую функцию

U l ( 5 ) = 1 + u ^{( 1} ) s^{l 1} + U ^1 s ¹ + ...

можно получить непосредственно из рекуррентного соотношения (7):

ТГ/\ ,   ¹ J ( sx ) '

U, (s) = 1 + j (1 -

1^{1 -1}          /

-V + s

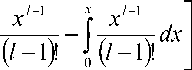
+ .3 dx ,

+ s

1 + 1

x 1 - 1      x

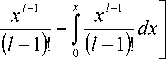
Приводя подобные по степеням x и суммируя образующиеся геометрические прогрессии с показателем s , получим:

U 1 ( s ) = 1 + -L

1 - s

—

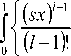
^{( sx} ) ¹ ₊ l !

/ \ 2 1 -2     / \2 1 -1

( sx )       ( sx )

( 2 1 - 2 )! ( 2 1 - 1 )!

+ ... ^ dx

Выражение под интегралом в (9) представляет собой ряд Макларена функции

ψ_l ( sx ) , которая является решением рекурсивного уравнения, соответствующего (7):

x

Yt (x) + j^1 (x) dx +... + xx

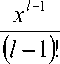
или d1 2^ 1 d1 3^1 dx1-2 dx1-3

dψ

...

dx

+ ^ = x .

В компактной записи соотношение (9) примет вид:

1 ¹                                1 ^s

U ( s ) = 1 +-- y ₁ ( sx ) dx = 1 + —7---- x v ₁ ( x ) dx

^{1 - s} 0                    ^{s ( 1 - s} ) 0          .

Переходя к производящей функции хвостов времени возвращения, получаем:

Qi ( s ) =------ ¹------

’   (1 - s ) U 1 ( s )

s

S s (1 - s) + j^ (x) dx

Рассмотрим уравнение (10) для случая > 2. Данное уравнение представляет собой неоднородное линейное с постоянными коэффициентами (все равны 1). Его частный интеграл имеет вид:

l//( x ) = x - 1 .

Общий интеграл однородного уравнения будем искать с помощью преобразования Лапласа. Исходя из вида уравнения (10) получаем характеристическое уравнение:

1 + q + q ² + ... + q ^{1 - 2} = 0         (13)

Корни уравнения (13) в Эйлеровом тригонометрическом виде образуют группу по умножению:

qk = e * , k = 0,1,...,1 -2, за вычетом точки q0 = 1.

Таким образом общий интеграл (10) получаем в виде:

I - 2

1 / 1 ⁽ x ) = x ^{- 1} + £ b k e^xqk .       (14)

k = 1

Неопределенные коэффициенты bk , k = 1,...,1 - 2 находим из однородных на чальных условий в точке x = 0 :

dk - / 1 , . k - 1      0

Таблица 2. Средние и дисперсии числа трендовых серий

l	2	3	4	5	> 6
µ n - 1	0,5	0,132	0,034	6,9 ■ 10 - 3	l ( l + 1)!
σ 2 n - 1	0,074	0,060	0,026	6,5 ■ 10 - 3	l ( l + 1)!

Для l = 2 ^ 5 получим:

1— i1

x ,          (л + i e " ~ x +(Л - i e " ~ x.

i /₂ = x , ^ = e + x - 1,        ^ ₄ = ^А-------------f------------+ x — 1,

^ =1 e -x + — eix + — e " x + x — 1. 52       44

При больших l можно получить асим-тотическую оценку ψ_l ( x ), вполне удовлетворительную для поставленных целей, и, соответственно, оценки искомых числовых характеристик числа серий.

Рассмотрим более детально ряд Маклорена функции ψ_l ( x ) .

Исходя из вида уравнения (10) следует, что последовательность производных ψ_l ( x ) в нуле имеет период l - 1, а именно, отличны от нуля только члены, кратные l - 1 и на “1” старше. Причем, все члены первой подпоследовательности равны “1”, второй – “-1”.

Поскольку члены ряда имеют факториальную скорость убывания, то на интервале x е [ 0;1 ] главным значением ряда будет сумма двух первых членов, а остаток можно оценить порядком третьего (первого отброшенного) члена:

, А - x ¹ - *      x l          x 2 ⁽ l - 1) .

^{V l (} x ) ( l - 1 )! l ! ⁺°⁽ ( 2 l - 2 )! ) .

Откуда получаем асимтотические оценки:

^{l - 1}     f. ^l

^ l ⁽¹⁾* "T ’ f l ^{( x} ) ^dx *(m)!• (15)

Далее, на основании (8) и (4) находим среднее и дисперсию времени возвращения трендовой серии:

- 1

^ T, = 3 ^ T ^{+[ 1 —} 2 ^1 ⁽¹⁾ K

^ t

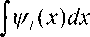
При использовании теоремы Мизеса-Феллера следует учесть, что длина цепи последовательных разностей на 1 короче длины исходной выборки. По этому формулы для числовых характеристик числа серий будут несколько отличаться от (5):

n - 1          ₂     ⁽ n ^{- 1) ct} t

^R ( l ) * ,      ^gr ( l ) *T

^Rn       Mt,             ^Rn     ( 1 + M t, ) ^. ( 7)

Подставляя в (17) (16) и (15), получаем оценки числовых характеристик числа серий при больших l :

µ(l)    σ2(l)        l nn n-1 ~ n-1 ~ (l +1)!

Для практических целей полученными Пуассоновскими оценками (18) с достаточной точностью можно пользоваться уже начиная с l =6. Точные значения числовых характеристик для коротких серий приведены в табл. 2.

Результаты статистического моделирования представлены на рис. 2. Как и в предыдущем случае, гистограммы числа возрастающих трендовых серий построены по 200 реализациям. Сглаживающие кривые – функции Гаусса с числовыми характеристиками (17).

Как видно из представленных на рис.1, 2 графиков, отличие в структурах серий разных типов лишь количественное, заключающееся в различии рядов средних и дисперсий. Практически полное совпадение наблюдается лишь при l = 4 (табл.1, 2.) При этом число, а точнее поток серий имеет отчетливую спектральную структуру. Количество различимых спектральных полос и их контраст- ность возрастают пропорционально n . Такое свойство структуры серий позволяет установить надежный критерий случайности –

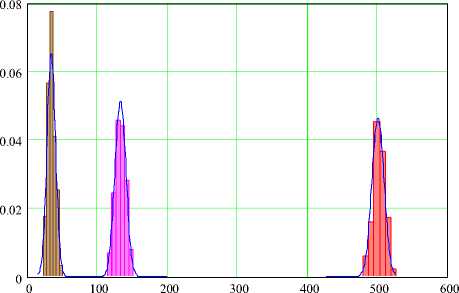
Рис. 2. Распределение числа восходящих трендовых серий в выборке объема n=1000 в зависимости от длины серии 1 = 2 ^ 4

отсуствие инверсий среди контрастных спектральных полос. Или, другими словами, наличие хотя бы одной инверсии в спектре числа серий можно обоснованно интерпретировать, как искусственное упорядочение последовательной выборки.

В заключение следует указать на еще один интересный эффект в структуре серий случайной последовательности – наивероятнейшее появление серии в первом из возможных исходов. Это явление, природа которого, по видимому, имеет нечто общее с “Петербургским парадоксом” [1], обусловлено тем, что ряд распределения времени возвращения f (¹ ) = P { T _l = n } монотонно убывает, и первый отличный от нуля член ( n = 1 ) является существенно доминирующим [1, 3].

Другим, более значимым проявлением указанной закономерности является “притя- жение” длинных серий (преимущественно разного знака). Дело в том, что в рекуррентной трактовке любая конечная последовательность рассматривается как отрезок бесконечной в обе стороны последовательности, и после точки, завершающей очередную серию, отсчет начинается заново. В связи с этим максимальным правдоподобием среди возможных расположений двух или более серий в отрезке последовательности обладает конгломерат, то есть имеет место “эффект притяжения” серий. И напротив, большое расстояние между сериями является маловероятным, а, если наблюдается, то может свидетельствовать о неслучайном характере последовательности.