Об использовании стробоскопических выборок при анализе движения ионов в квадрупольных радиочастотных полях. II. Исправление концепции

Данная работа является прямым продолжением публикации [1], посвященной критическому анализу результатов [2]. Номера формул и рисунков из публикации [1], на которые ссылается данная статья, снабжены префиксом "I" и имеют вид (I.1), (I.2) и т. д.

ИСПРАВЛЕНИЕ КОНЦЕПЦИИ ЭФФЕКТИВНОГО ПОТЕНЦИАЛА

ДЛЯ СТРОБОСКОПИЧЕСКИХ ВЫБОРОК

Рассмотрим, как можно исправить предложенную в [2] концепцию эффективного потенциала для описания движения ионов в квадрупольном фильтре масс в произвольной рабочей точке и при произвольном профиле радиочастотного сигнала, одновременно устранив перечисленные в [1] недостатки. Для этого будет использоваться математическая модель движения заряженных частиц в квадрупольных радиочастотных полях, предложенная в [3, 4] и основанная на представлении точных решений линейных дифференциальных уравнений с периодическими коэффициентами с помощью матриц Флоке—Ляпунова, выраженных через матрицы монодромии.

В безразмерных координатах в квадрупольном радиочастотном поле движение x ( t ) по координате x для иона с массой m и зарядом e описывается уравнением Хилла (воспроизводим с нумерацией из [1])

dj ^x + ( a + 2 qf ( ^ ) ) x = 0, (I.1) где ^ = Q t / 2 — безразмерное время, a = 8 eU 0/ m О ² r ₀ ² и q = 4 eV ,/ m Q ² r ₀ ² — безразмерные параметры, f ( ^ ) = F ( 2 ^ Q ) — периодическая функция с безразмерным периодом T' = п (безразмерной круговой частотой О’ = 2). Для квадруполя c косинусоидальным радиочастотным напряжением f ( ^ ) = cos ( 2 2 + ф ₀ ) , где ф ₀ — фаза радиочастотного напряжения в момент старта иона, уравнение Хилла превращается в уравнение типа Матьё.

Внутри зоны устойчивости вследствие того, что для коэффициентов матрицы монодромии выполнено неравенство -2 < mxx + mvv < 2 и определи тель матрицы монодромии mxxmvv - mxvmvx равен единице, коэффициенты матрицы монодромии могут быть выражены с помощью вспомогатель- ных параметров βx , λx , µx по формулам [5, 6]

mxx = COS пвх - Hx sin пвх , mvv = COS nex + Hx sin nex , mxv = Ax V1 + ^x sin nex, mVx =- Л/1 + Hx2 sin пв A , vx                 x          x x где

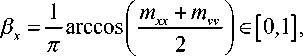
т -т„ vv xx

Стробоскопическая выборка отсчетов x n -- х ( nT ' ) , v_n - v ( nT ') в соответствии с [1, (3, 4)]

µ

2sin πβ _x

подчиняется соотношениям

x n

Vvn J

- M"ⁿ

Cx° 1

V ^v 0 J

, где

mxv

^Х   /--------- .

x 2

4 1 + Ц sin ^пв х

x ₀ - x ( 0 ) , v ₀ - v ( 0 ) — начальные значения.

Для матричной функции

S x ( 5 ) -

cos A ^{5 -} Ц x sin A ⁵ v ^- 71 + ^ 2 sin aa/a

К 71 + ^ 2 sin AA cos в5 + Ц_x sin в5 J

выполнены соотношения M_x - S_x ( T ') и S x ( 5 ) S x 5 ) - S x ( 5 + 5 2 ) , так что M X -- S_x ( nT ') . Теперь дискретная выборка x_n , v_n естественным образом доопределяется для любых промежуточных моментов времени с помощью функций X ( 5 ) , V ( 5 ) , заданных по формуле

f x5 1 1

А) -Фx(5)Sx(-5)Sx(-) „0J-

Vv(5)J                          Vv0 J

- ^Л x ( 5 )

X -)

V V (5) J

f X($*1

V V ( 5 ) J

Sx (5)'

V v 0 J

т. к. x_n - X ( nT ') и v_n - V ( nT ') , где X ( 5 ) и V ( 5 ) — синусоидальные функции.

Выражения (3), (4) выглядят математическим трюком, но в действительности эти формулы описывают синусоидальные секулярные колебания с секулярной частотой β_x . Действительно, пусть фундаментальное решение X_x ( 5 ) , V_x ( 5 ) уравнения (I.1) удовлетворяет начальным условиям X_x ( 0 ) - 1 , V_x ( 0 ) - 0 , а фундаментальное решение X . ( 5 ) , V v ( 5 ) удовлетворяет начальным условиям X_v ( 0 ) - 0 , V_v ( 0 ) - 1 . Коэффициенты матрицы монодромии M_x для [1, (4)] определяются как m x - X_x ( T ') , m_vx - V_x ( T ') , m_xv - X_v ( T ‘ ) , m_vv - V v ( T '), а общее решение (I.1) можно записать как

поскольку для матрицы (3) справедливо тождество S x ( 5 . ) S x ( 5 2 ) - S x ( 5 . + 5 2 ) и, следовательно, матрица S_x ( - 5 ) S_x ( 5 ) будет единичной.

В силу периодичности коэффициентов уравнения (I.1) пары функций X_x ( 5 + T ' ) , V_x ( 5 + T ') и X_v ( 5 + T '), V_v ( 5 + T ') также являются ее решениями и их можно представить как суперпозицию фундаментальных решений, т. е. в виде равенства

fXx (5 + T') Xv (5 + T')J

V Vx (5 + t ')   Vv (5 + t ')J

-f Xx ( 5 ) Xv ( 5 )Jf mxx mxv 1

V V x ( 5 ) V v ( 5 ) JV m vx m vv J ,

fx5 - fX 5> xvOfx0J V v (5 )J V Vx (5) V, 5 )JV v 0 J

Ф x (5 )

A ^x 0

V v0 J

, (5)

где Ф _x ( 5 ) — матрица фундаментального решения. Выражение (5) также можно записать как

(для проверки достаточно убедиться, что правая часть соотношения (7) обеспечивает для функций X x ( 5 + T ’) , V x ( 5 + T ') и X v ( 5 + T ') , V v ( 5 + t ’) правильные начальные условия в точке 5 - 0 , и воспользоваться утверждением о единственности решения обыкновенного дифференциального уравнения с заданными начальными условиями). В результате матрица Л _x ( 5 ) -Ф _x ( 5 ) S_x ( - 5 ) оказывается периодической с периодом T' :

л x (5 + t ')-ф x (5 + t ') Sx (-t '- 5 )-

-Ф x ( 5 ) S x ( T ') S x ( - T ') S x ( - 5 ) -

= Ф , ( ? ) S x ( - ? ) = л , ( ? ) ,          (8)

поскольку ^ф x ⁽ ? + T ') = ^ф x ⁽ ? ) M x , M x = S x ⁽ T ')

И V ?„ ^ 2 : S x ( ? , ) S x ( ? - ) = S x ? + ? - ) . ПО СУТИ представление решения x ( ? ), v ( ? ) в двухступенчатом матричном виде

Гл„(?) лxv(?)YX(?Ъ (л.(?) л„(?)АV(?))

л x ( ? )

(

X? h v ? ) J

Г X?)Т ( v (? )J

^Г cose? - H x sin в? л . ^ sin ^в ? )Г x 0' ( ^- V ^{1 +} H x ² sⁱⁿ P?P cos P x ? ⁺ H x ^sin P x ? ⁾ ( v 0 J

где л _x ( ? ) — периодическая матрица с периодом T’ , не зависящая от начальных условий и обращающаяся в единичную при ? = 0 , является представлением Флоке—Ляпунова для линейных дифференциальных уравнений с периодическими коэффициентами [7–11].

Поскольку матрица л _x ( ? ) = Ф _x ( ? ) S_x ( - ? ) является периодической, ее достаточно вычислить численно для одного периода времени. После этого формула (9) позволяет вычислить точно решение x ( ? ) , v ( ? ) для любого момента времени без привязки к стробоскопическим дискретам ? n = nT ', а истинное движение x ( ? ), v ( ? ) разбивается на секулярное движение X ( ? ), V ( ? ) , заданное аналитически, и на периодическое радиочастотное возмущение, заданное матрицей л ( ? ) .

Функции X(?),V(?), заданные в соответствии с (3), (4), представляют собой общее решение системы стационарных дифференциальных уравнений dX? = (-HxPx)X(4)+(Х.Р.Х+й5-)V(?).

-d ? = ( - e x   +< /х ) X ? ) + ( ha ) ^v ( ? )

с начальными условиями X ( 0 ) = x ₀ , V ( 0 ) = v ₀ .

Из (10) следует, что X(?) удовлетворяет дифференциальному уравнению d--X? + ex X (? ) = 0, (11)

которое не совпадает с (I.16) даже с учетом разных масштабов для безразмерного времени ξ и индексов стробоскопических отсчетов n = п? .

Уравнение (11) можно интерпретировать как движение механической частицы с единичной массой в поле с безразмер н ым эффективным механическим потенциалом U_x ( ? ) = в ;^- ? ²/- . Преобразования для движения по координате y ничем не отличаются от преобразования движения по координате x , за исключением замены матрицы монодромии M_x на матрицу монодромии M_y для уравнения (I.2). Отсюда, в частности, следует, что поскольку частоты в уравнениях (I.16) и (11) отличаются, а функции X ( ? ), V ( ? ) в точности интерполируют стробоскопические отсчеты, то, за исключением вырожденного случая в_у = 0 , функции Y ( n ), W ( n ) , вычисленные из уравнений (I.15), (I.16), будут быстро расходиться с истинными стробоскопическими значениями y_n , w_n .

Инвертирование координат и скоростей после умножения на M_x с заменой P_x на 5_x = 1 - P_x позволяет построить континуальный аналог для описания биений:

S x ( ? ) =

cos ^? + H sin Pt? xxx

( V^{1 +} H x ² sin 5 x?/ ^X x

- X >11 + H- sin Pt?Л xxx cos P? - H sin Pt? J xxx

где M_x” = ( - 1 ) ⁿS_x ( nT ‘ ) , функции X ( ? ) и V ( ? ) , заданные с помощью условия

Г ^X ( ?t

( V (? )J

= S x ( ? )

^x 0

( ^v 0 J

представляют собой синусоидальные функции, а для стробоскопических отсчетов выполняются точные соотношения xn - (— 1) nX (nT'), vn --(-1)У(nT■). Матрица A,(5)=Ф.(5)У(-5) удовлетворяет условию Л x (5 + T') - -Л x (5 ), функция X(5), описывающая биения, удовлетворяет дифференциальному уравнению d2 X (5)/d52 + 3, X (5) - 0, а точная траектория x 5 ), v 5 ) может быть представлена как биения X (5), V (5), подвергнутые линейному периодическому радиочастотному преобразованию, задаваемому матрицей Лx (5). Однако в этом нет особой необходимости, поскольку вся нужная информация может быть извлечена из секулярных колебаний. Отметим только, что соответствующие дифференциальные уравнения снова будут заметно отличаться от уравнений (I.12) и (I.13), полученных в [2]. Поэтому, за исключением вырожденного случая в, - 1, функции X (n), V (n), вычисленные из уравнений (I.12), (I.13), и истинные стробоскопические значения (-1)” xn, (-1)” vn, будут достаточно быстро рас ходиться.

Система уравнений (10) представляет собой гамильтоновы уравнения движения с эффективным гамильтонианом секулярного движения H ( У , X )- ^IxEB-у ² — ^VX + ^ ^E K x ² . (13) 2            ^{x x}        2 λ_x

Тот факт, что гамильтониан секулярного движения X ( 5 ) V ( 5 ) , заданного уравнениями (10), не распадается на сумму кинетической и потенциальной энергий, является неустранимым свойством. Из представления Флоке x ( 5 ) -- g ( 5 ) ( C a exp ( iP5 ) + C b exp ( - i P5 ) ) , где функция g ( 5 ) является периодической с периодом T ', следует, что вычисленная в точках 5_п - nT ' секулярная скорость         v ( 5_n ) — d x ( 5_n ) Jd 5 -

— c‘ exp (iP5n) + cb exp (-iP5n) будет неизбежно отличаться от формальной производной для вычисленной в стробоскопических точках 5 — nT' секулярной координаты x (5n) - ca exp (iP5n) + +cb exp(-iP5n) (надо учесть, что для стробоскопической выборки g (5n ) -1 и g '(5„ ) ^ 0 — кон- станты, не зависящие от индекса n). Это связано с тем, что секулярная скорость и секулярное движение — вспомогательные математические конструкции, лишь опосредованно связанные с истинным движением.

В процессе движения, описываемого уравнениями (10), гамильтониан (13) остается константой. Максимальное отклонение секулярных траекторий X ( 5 ) , У ( 5 ) для заданных безразмерных начальных условий x ₀ , v ₀ определяется из соотношений

H ( V о , X о ) - H ( V max , X m_ax )----- ^P      X max ,   (14)

2 x 71 + M 2

где ^У max ^- M x /[^ x 7^{1 +} M X ) ^X max ^бе р ^{ется из (10)} при наложении условия d X _max ( 5 ) [d5 - 0, соответствующего максимальному отклонению X ( 5 ) от оси квадруполя. То есть

(                       )

^X max ^{- ( 1 +} M x " ) ^ x^V 02-- \ ^V 0 x 0 ⁺ x 02

t 71 + m F        )

где v ₀ - d x ( 5 ) jd^^-Q имеет ту же размерность, что и x 0 ^- x ^{( 5} ) _{5 - 0} , а параметры ^e x , ^ x , M x и ^{5 —} безразмерные. (Для начальных условий уравнений (10) и (I.1) используются одни и те же обозначения, поскольку они и в самом деле совпадают: в условии (6) матрица Л ( 5 ) при 5 - 0 — единичная.)

Остается определить, как связаны между собой максимальные отклонения от оси квадруполя для секулярных колебаний X ( 5 ), У ( 5 ) и для истинных движений x ( 5 ), v ( 5 ) . В соответствии с (9),

^x ( ⁵ ) ^-Л xx ( ⁵ ) ^х

х ( x 0 ( cos P x ^{5 -} M x sin ^e x ⁵ ) ^{+ V} 0 ( X x J ^{1 +} M x 2 sin P x ⁵ ) ) ⁺

+Лxv (5)х х x0 (-71 + Mx2 sin Px5Xx )+ v0 ( cos Px5 + Mx sin px5)).

^x                            (16)

Тогда

x2 (5)-X0 (5) + Xc (5) cos2Px5 +

+ X s ( 5 ) sin2 P x 5 -

- X 0 ( 5 ) + X r ( 5 ) cos ( 2P x 5 - Ф R ( 5 ) ) ,       (17)

где V r ⁽ 4 ) = arctan ( X s ⁽ 4 ) / X c ( 4 )) , ^x r ( 4 ) = = 7 X 2 ( 4 ) + x; ( 4 ) , а X 0 ( 4 ) , X c ( 4 ) , X s ( 4 ) выражены через функции Л _хх ( 4 ) , Л _xv ( 4 ) и будут периодическими с периодом Т ' .

Если периоды Т' _х = 2лв_х и Т' = п в достаточной степени несоизмеримы (т. е. их отношение не является простым рациональным числом), то в последовательности чисел 4 k * = 4 * + kT ' (где 4 * е [ О, Т '] — произвольное фиксированное значение), для членов которой функции X ₀ ( 4 ) , X_c ( 4 ) , X s ( 4 ) принимают постоянные значения ^X 0 ^{( 4} * ) , ^Xc ^{( 4} * ) , ^Xs ^{( 4} * ) , найдутся такие числа ⁴ * ,что cos ( 2 P x ⁴ k * - v _r ) будет сколь угодно мало отличаться от единицы. Это означает, что максимум выражения (17) равен величине X ₀ ( 4 * ) + X_R ( 4 * ) , максимизированной по периоду 4 * е [ О, Т ' ] (исключениями будут точки a , q , для которых β_x — простая дробь). Поскольку X R ( 4 ) = X c ( 4 ) + X ;( 4 ) - X О ( 4 ) , а X 0 ( 4 ) раскладывается на два множителя, один из которых зависит от х ₀, v ₀ , а второй от Л _хх ( 4 ) , Л _xv ( 4 ) , то условие, что х ² ( 4 ) не превышает r ₀ ² (квадрата нормированного радиуса апертуры квадруполя), приобретает вид:

При этом для тех точек a , q , где отношение секулярной частоты β_x к частоте радиочастотного возбуждения близко к отношению двух небольших целых чисел, оценка (18), (19) будет чрезмерно пессимистической, а реальный аксептанс будет заметно больше этой оценки и не будет иметь эллиптическую форму [3, 17].

Условия (18), (19) позволяют определить безр а змер н ую глубину псевдопотенциальной ямы D_x = V_x ² /2 (максимальную кинетическую энергию, для которой ион, стартующий с оси квадруполя, еще удерживается радиочастотным полем в пределах апертуры квадруполя при любой начальной фазе радиочастотного поля) и бе з размерную ширину псевдопотенциальной ямы R_x (максимальный начальный сдвиг иона от оси, для которого ион, стартующий с нулевой кинетической энергией, еще удерживается радиочастотным полем в пределах апертуры квадруполя при любой начальной фазе радиочастотного поля):

max x

4 e ( —rn , +rn )

2 (4 ) = Л L (1 + нх )х

X х о² + Л,² V о² к

—

^

2 λ_xµ_x

/------7 ^х о ^v о

ДН J

^{- r} 0² , (18)

^л m _a x

= max Л^ (4) + —

4 е ( о, т ■ )                      5 ²

к

λ x

Л 2v (4) +

2 µ

+----/

Л х V1 + Н

Л

Л uu ( 4 ) Л uv ( 4 ) .

После сравнения (18), (19) с (15) ясно видно, что Л _max определяет, во сколько раз радиочастотное возмущение масштабирует амплитуду секулярных колебаний. Так как Л _хх ( о ) = 1 и Л xv ( 0 ) = 0 , то Л max >  1 .

Уравнения (18), (19) описывают фазовые эллипсы аксептансов для фиксированной начальной фазы радиочастотного поля и отличаются от фазовых эллипсов в [12–16] лишь обозначениями.

начальной фазы ϕ ₀ ), где выражение (20) пересчитано к максимальной начальной безразмерной скорости вместо максимальной начальной кинетической энергии. Зная V_x и R_x , можно оценить минимаксный аксептанс πV_x R_x при движении по оси x , если его можно аппроксимировать фазовым эллипсом (, х ₀ / V_x ) 2 + ( х ₀ ^К_х ) 2 - 1 .

Движение по направлению y , которое описывается уравнением (I.2), разбирается аналогичным образом. Поскольку процессы движения ионов в радиочастотных квадруполях в условиях устойчивости вполне определяются секулярными частотами ω_s , нет необходимости рассматривать еще и частоты биений to b = ( Q — 2to_s )/2 , по сути представляющие из себя некоторую математическую фикцию. Однако предложенная в [2] запись секулярных уравнений в безразмерной форме с биениями (что сводится к замене в уравнении ⁽¹¹⁾ Р х ^{на 1 —} Р х , Н х ^{на —} Н х , ^Л х ^{на — Л} х ) ^имеет то преимущество, что при в_х « 1 малый параметр

V x 2	2 =           Г     ro      '       п max [ Л 2 ( 1 + н 2 ) Л 2 тах ] , x       x    max Ф 0 е1 0,2 п ]	(20)
R x 2	2 = r 0 max 1 ( 1 + н 2 )Л2х 1 Ф ое [ О,2 п ]LV     ^х/ max"1	(21)
(каждый	из параметров Л х , Н х , Л max	зависит от

1 — в_х , задающий степень близости рабочей точки к границе зоны устойчивости, входит в уравнения в явном виде.

ДВИЖЕНИЕ ИОНОВ В РАДИОЧАСТОТНОМ КВАДРУПОЛЕ В ОКРЕСТНОСТИ ВЕРШИНЫ ПЕРВОЙ СОВМЕСТНОЙ ЗОНЫ УСТОЙЧИВОСТИ

Рассмотрим на основе предложенной в предыдущем разделе теории поведение движения иона в окрестности вершины первой совместной зоны устойчивости косинусоидального линейного квадруполя. Координаты вершины задаются как ac = 0.236994 , qc = 0.705996 [2], а 5a = a — ac и 5q = q — qc — отклонения рабочих параметров a,q уравнений (I.1), (I.2) от вершины ac,qc . Для определения матрицы монодромии (I.3) будем находить численно базовые решения Xx (5 ), Vx (5), Xv(5), Vv(5) уравнения (1.1):

5 X 20) = 0,	f V v f0 ) = 0,
д a	д a
д X 8 v =д V v_ д q    д q ’	8 -qx = —( a + 2 q cos ( 2 5 + ф 0 ))^
	— 2cos ( 2 5 + Ф о ) X v ,
a X v (2 ) = 0,	V 0 ) = 0,
д q	д q

—

(способ аналогичен методу тау-вариаций, предложенному в [18, 19]).

Операции с периодическими функциями ^Л xx ^{( 5} ) , ^Л xv ^{( 5} ) , ^Л vx ^{( 5 )} , ^Л vv ^{( 5 )} можно Упро стить, если учесть, что для первой зоны устойчивости определяющими членами в них являются первые гармоники cos2 ξ , sin 2 ξ , а старшие гармоники обеспечивают лишь незначительные поправки, и их вклад на порядок отличается от основных гармоник:

X x = V x ,    V x =— ( a + 2 q cos ( 2 5 + Ф о ) ) X x ,

X v = V x ,    V , =- ( a + 2 q cos ( 2 5 + Ф о ) ) X_v ,       (22)

X x ( 0 ) = 1,    V x ( 0 ) = 0, X v ( 0 ) = 0, V x ( 0 ) = 1.

Л xx ( 5 ) * 1 — ^ ’( 1 — cos 2 5 ) + B xx > sin 2 5 —

^{— A}xx ( 1 ^{— cos4 5} ) ⁺ B xx sin ^{4 5 +} - ,

Для того чтобы определить вариации коэффициентов матрицы монодромии при варьировании рабочих параметров a , q , добавим к системе уравнений (22) дополнительные функции 8 X x ( 4 )/8 a , 8 V x ( 5 )/8 a , 8 X x ( 5 )/8 q , 8 V x ( 5 )/8 q , 8 X v ( 4 )/8 a , 8 V v ( 5 )/8 a , 8 X v ( 5 )/8 q , д V_v ( 5 )/д q , ... (при необходимости до второго порядка включительно) и соответствующие им дополнительные уравнения:

Л xv ( 5 ) *— A xv *( 1 — cos 2 5 ) + B xv ’ sin 2 5 —

^{— A}x ² ) ( 1 — cos ^{4 5} ) ^{+ BV}xv ²⁾ sin ^{4 5 +} ■■•,   (24)

Л vx ( 5 ) -— A ( 1 ) ( 1 — cos2 5 ) + B v 1 ) sin 2 5 —

д X_x = д V_x д a     д a ’

д V_x д a

д X

— (a + 2 q cos (25 + фо)) —x — Xx, д a

5 X dS = 0,   f V f⁰ ) = 0

д a          д a

д X_x = д V_x д q    д q ’

= —(a + 2 q cos (25 + фо ))-^

—

— 2cos ( 25 + Ф о ) X x ,

^— A vx ^!)(1 ^{— cos4 5} ) ⁺ B™ ^!) sin ^{4 5 +} ^ ,

Л vv ( 5 ) * 1 — A ( 1 ) ( 1 — cos2 5 ) + b v 1 ) sin 2 5 —

— Av v2) (1 — cos45) + bv v2) sin 45 + • -, где учитывается Л xx (0)= 1, Л xv (0) = 0, Л vx (0) = v, Л vv (0) = 1. При этом следует отметить, что хотя по отдельности величины Xx (5), Vx (5 ) , Xv (5 , Vv (5 ) , ex , Mx , Xx ведут себя как функции параметров a, q при приближении к границе зоны устойчивости нерегулярным образом, но, как и коэффициенты матрицы монодромии, функции Л xx (5) , Л xv (5 ) , Л vx (5 ) , Л vv (5 ) вполне

дXx ( 0 ) = 0   д Vx ( 0 ) = 0

д q      ’     д q

д X v J^V, д a    д a ’

д V v д a

д X

— ( a + 2 q cos ( 25 + ф о ) ) — — X_x , ^x                       ' д a

регулярны.

Из параметризации (9) и того факта, что функции x ( 5 ) , v ( 5 ) = d x ( 5 ) /d 5 удовлетворяют дифференциальным уравнениям (I.1) при f ( ^{5 )} = cos ⁽ 2 ⁵ + Ф 0 ) , следует, что ^Л xx ^{( 5} ) , Л xv ( 5 ) , Л vx ( 5 ) , Л ( 5 ) удовлетворяют диффе-

ренциальным уравнениям

Х х ( 5 ) = в х М х Л хх ( 5 ) +

, ^вх 71 ⁺ ^х к ( к \ , к ( с\

⁺ _Х ----Л хх ^{( 5} ) + Л _m⁽ ^ ) ,

A Xv ( 5 ) = - в х ^ х 1 +^ Л хх ( 5 ) -

- в х М х Л хх ( 5 ) + Л vv ( 5 ) , ^л Хх ( ⁵ ) = ^- ( a ^{+ 2} q cos ( ^{2 5 + ф} о ) ) ^л хх ( ⁵ )⁺

+ в х М х Л хх ( 5 ) + ^вх ^^ Л vv ( 5 ) , Х х

^A vv ( ⁵ ) = ^- ( a + ² q cos ( ^{2 5} + ^ф 0 ) ) л хх ( ⁵ )^-

_          - в х Х х 71 + ^ 2 Л хх ( 5 ) - в х М х Л vv ( 5 ) .

Подстановка (24) в (25) приводит к чисто алгебраическим соотношениям для неизвестных коэффициентов А хk ^, В хk ^, • ••, откуда их легко можно вычислить.

Совместное численное решение уравнений (22), (23) для ф0 = 0 дает для коэффициентов матрицы монодромии M x аппроксимацию тхх ~

» -1.000000 -5a - 2.527266 -5q - 2.917327 + • •, тхх »

» + 3.750278 - 5 a - 5.181347 + 5q - 2.091033 + • ,

^, (26)

^тхх »

» +0.000000 + 5a -1.347775 + 5q - 1.555792 + •, mvv »

» - 1.000000 - 5a - 2.527267 - 5q - 2.917327 + • .

Отсюда следует, что вх *

» 1.000000 - 0.715633V - 5a - 1.154341 5q ,

Mx » 0,                                         (27)

Хх *

~ 1.668104 - 2.304636 5a + 0.930080 5q

~         -5a - 1.154341 5q

(поскольку (1/ n ) arccos ( - 1 + 5 ) « 1 - ( V2/ п \[5 ). В первом приближении вариация положения рабочей точки должна удовлетворять условию - 5a - 1.1543415q >  0 , чтобы оказаться внутри зоны устойчивости по x .

Как следует из [1, рис. 1, а], в окрестности вершины совместной зоны устойчивости для движения по координате x максимум величины (20) достигается при ф ₀ = 0 (см. также [2, 20]). Тогда максимум величины (19) достигается в точке 5 = 0 и равен единице. Оценка (20) дает с точностью до квадратичных поправок

₂ ^ _₂ ( - 5a - 1.154341 5q ) ^: ~ r⁰      2.782571

Эта оценка в целом совпадает с оценкой глубины псевдопотенциальной ямы для координаты x из публикации [2], но только если используется значение ет_хЬ = п ( 1 - в_х ) вместо ® хь = ^{2cos пв} х /2 .

Вычисление матрицы монодромии My для движения по оси y в окрестности вершины зоны устойчивости (23) при ф0 = п дает аппроксимацию myy ”

» +1.000000 - 5a • 6.205798 + 5q • 3.972621 + •, myw »

» + 6.821373 - 5a • 7.922811 - 5q • 2.838210 + • , (29) m wy “

» +0.000000 - 5a-1.819516 + 5q-1.164757 + •, mww »

» + 1.000000 - 5a - 6.205798 + 5q - 3.972621 + • .

Отсюда следует, что ву « 1.12140975a - 0.6401475q,

M y « 0,                                        (30)

Х ~ 1.936234 - 2.2488765a - 0.8056215q y ~        ^5a - 0.6401475q

(поскольку       ( 1 п ) arccos ( 1 - 5 ) « ( V2/ п )V 5 ).

В первом приближении вариация положения рабочей точки должна удовлетворять условию 5a - 0.640147 5q >  0 чтобы оказаться внутри зоны устойчивости по y .

Как следует из [1, рис. 1, б], в окрестности вершины совместной зоны устойчивости для движения по координате y максимум величины (20) достигается при ф0 = п (см. также [2, 20]), причем для этой фазы максимум величины (19) дости- гается в точке ^ = 0 и равен единице. В соответствии с оценкой (20) с точностью до квадратичных поправок

V 2 ~ _₂ ( 5a - 0.640147 5q ) y ~ r⁰     3.749003

.

Эта оценка в целом совпадает с оценкой глубины псевдопотенциальной ямы для координаты y из публикации [2], но только если используется значение ю = пВ, вместо ю = 2 sin пВ, /2 .

ys        y               ys                y

Вычисление ширины псевдопотенциальной ямы будет не намного сложнее. Как следует из [1, рис. 1, в] (см. также [20]), в окрестности вершины совместной зоны устойчивости для движения по координате x максимум величины (21) достигается при ф ₀ = п /2 . Совместное численное решение уравнений (22), (23) при ф ₀ = п /2 дает аппроксимацию для коэффициентов матрицы монодромии ^l

M x :

4- mxx ”

» 0.803639 - 5 a • 3.760821 - 5q • 0.631918 + • • ,

4- mxv »

» + 1.344081 - 5 a • 3.714615 - 5q • 1.992345 + ■ • ,

_                                                     , (32)

m vx »

» - 2.420326 + 5 a • 0.382213 - 5q • 5.380316 + • ,

^4

m vv »

» - 2.803639 - 5a • 1.293712 - 5q • 5.202736 + • .

Отсюда следует, что

B x =

= e x » 1.000000 - 0.715633V - 5a - 1.154341 5q ,

-0.401124 + 0.2743395a - 0.5082695q(33)

V-5 a - 1.1543415q’

1.490410 - 4.119022 5a - 2.20925 15q

1 - 7.5828595a - 4.6400185q"

Вычисление коэффициентов Фурье для периодической матрицы Л _x ( ^ ) дает аппроксимацию:

j XX >»- 0.181720 +

+ -0.198896 + 0.3269465a - 0.02687535q 7-5a - 1.1543415q’

Bl XV ) «- 0.103534 +

+ 0.294714 - 0.3604755a + 0.07599605q 7-5a - 1.1543415q’

В XV 0.604030 +

• - 0.296437 + 0.0905267 5a - 0.394689 5q

  7-5a - 1.1543415q’

  Bl V 1 ) «- 0.399708 +

  • - 0.2230758 + 0.769068 5a + 0.378240 5q

    7-5a - 1.1543415q’

    j? V 1 ) «- 0.322444 +

    0.160021 - 0.0102023 5a + 0.2541 525q

    • -5a - 1.1543415q’

      ^4V 1 >« 0.419287 +

      • - 0.343924 + 0.0565688 5a - 0.574189 5q

        7-5a - 1.1543415q’

        j? V 1 >» 0.0216691 +

        0.238497 - 0.180302 5a + 0.105056 5q

        7-5a - 1.1543415q"

Для начальной фазы ф0 = п/2 и координаты x максимум величины (19) достигается в точке ^ = 3п/4 и равен xmax

« 2.348011 - 0.398533 5a + 0.019545 5q +

+ 0.1383417 - 5a - 1.154341 5q .

Поэтому в соответствии с оценкой (21) с точностью до квадратичных поправок r2 ^ _2 (- 5a - 1.1543415q)

^{x    r 0}       0.377797

.

В?XX >« 0.485882 +

- 0.197740 + 0.128612 5a - 0.250666 5q

V - 5a - 1.154341 5q

Этот результат очень сильно не совпадает с соответствующими результ а тами из публикации [2], 22

где предполагается, что R_x ~ r ₀ .

Как следует из [1, рис. 1, г] (см. также [20], в окрестности вершины совместной зоны устойчивости для движения по координате y максимум

величины (21) достигается при ф 0 = П 2 . Численное решение уравнений (22), (23) при ф ₀ = П 2 Дает аппроксимацию для коэффициентов матрицы монодромии M_y :

.-- myy -

• -    - 1.467732 - 5a • 4.625349 + 5q • 7.155349 + • •,

.-- myw -

• -    + 3.631194 - 5a • 6.068713 + 5q • 2.495370 + • ,

  -                                                        ⁽³ 7)

m wy ^-

• -    - 1.677052 - 5a • 4.072736 + 5q • 7.666445 + • ,

m ww ^-

• -    3.467732 - 5a • 7.786247 + 5q • 0.789892 + • .

Отсюда следует, что вy = py - 1.121409V5a - 0.6401475q,

^—

Ц у ^-

_- 0.350231 - 0.224304 5a - 0.451706 5q

~         5a - 0.640147 5q

^—

^ y

~ 2.942941 - 4.918454 5a + 2.022400 5q

~   V1 + 6.871627 5a - 7.798284 5q

Вычисление коэффициентов Фурье для периодической матрицы Л x ( ^ ) дает аппроксимацию:

A yy - - 0.123565 + 0.095522 5a + 0.286562 5q , 7 ^ - + 0.374432 + 0.365073 5a - 0.823364 5q , A yw - + 0.363644 - 0.289647 5a - 0.358930 5q , 7 W - - 0.121185 - 0.0319335 5a + 0.355190 5q , A w ) - + 0.748863 + 0.285615 5a - 1.362163 5q , 7? w ) -+ 0.116244 - 0.0978184 5a - 0.244715 5q , V A ww - - 0.242371 + 0.0800064 5a + 0.618280 5q , 7? ww - - 0.342098 + 0.295901 5a + 0.264479 5q .

Для начальной фазы ф ₀ = П 2 и координаты y максимум величины (19) достигается в точке ^ = П 4 и равен

^Л у max ^-

- 1.777564 + 0.720698 5a - 1.585773 5q .

Поэтому в соответствии с оценкой (21) с точностью до квадратичных поправок

_{2 -} _₂ ( - 5a - 1.154341 5q ) y ^- r 0      0.218039

Этот результат очень сильно не совпадает с соответствующими результ а тами из публикации [2], где предполагается, что R y - Г 0² .

ВЫВОДЫ

Рассмотренные в [1] аргументы вынуждают считать концепцию эффективного потенциала, предложенную в работе [2], не вполне доработанной. Альтернативный вариант квадратичного эффективного потенциала для движения ионов в радиочастотных квадрупольных электрических полях, рассмотренный в этой статье и в работах [3, 4], представляется более работоспособным. Поскольку результаты работы [2] активно используются ее авторами и в последующих публикациях (например, [21, 22]), то скорее всего и эти результаты нуждаются в определенной корректировке. В частности, представляется не совсем надежным использование методов теории возмущений при приближении к границам зон устойчивости, поскольку при в - 0 и в - 1 основные члены для уравнений (I.12), (I.13) оказываются фактически того же порядка малости, что и "малые" поправки, переносимые в правую часть уравнений. (Следует также отметить, что метод возмущений нельзя применять в точке резонанса, в том числе и параметрического резонанса, если предварительно не выделить и не перенести в основное уравнение члены возмущения, связанные с резонансными частотами [23, 24].) При этом необходимо подчеркнуть, что понятие глубины псевдопотенци-альной ямы, введенное авторами [2] в самом общем случае без применения обычно используемого допущения о малости параметра q и без привязки к конкретной модели псевдопотенциала, является важным вкладом в общую теорию движения ионов в радиочастотных электрических полях и заслуживает всяческого внимания.

Данная работа выполнена в рамках гос. задания № 007-00229-18-00 для ИАП РАН. Авторы благодарны Николаю Витальевичу Коненкову, Евгению Васильевичу Мамонтову, Анатолию Петровичу Щербакову, Михаилу Игоревичу Явору, Антону Леонидовичу Булянице и Владимиру Ефимовичу Курочкину за полезные консультации по данной тематике.