В настоящее время известно большое число работ, посвященных непараметрическому восстановлению функций регрессии по наблюдениям с ошибками [1; 2]. Однако при обработке реальных данных приходится сталкиваться с ограниченными неравномерными выборками переменных {xi, yi, I = 1, …, s}, содержащих сгущения, пустоты и разреженности в выборочном пространстве. В таких ситуациях классические непараметрические оценки кривой регрессии дают неудовлетворительные результаты, поэтому возникает необходимость введения новых непараметрических оценок функции регрессии, которые отличаются от известных использованием специальных ядерных функций. Исследуются также асимптотические свой- ства полученных оценок и приводятся результаты статистического моделирования.

Непараметрические оценки функции регрессии. Пусть ( x , y ) – случайная величина со значениями в пространстве Q ( x , y ) c R 2 , p ( x , y ) > 0 - плотность распределения двумерной случайной величины ( x , y ), она неизвестна, кроме того p ( x ) > 0. Дана выборка из s статически независимых наблюдений двумерной случайной величины ( x , y ) – ( x 1 , y 1 ), ( x 2 , y 2 ), … , ( x s , y s ).

Обычно за непараметрическую оценку функции регрессии принимают статистику [1; 2]

_Л| х — х, | v .| х - х, |

• y s ⁽ x ) = L У / ^ф|-^ 1/ ^ ^ф|      ^; I ,       ⁽¹⁾

• i =1        ^ C s ) i =1 ^ C s )

  где интегрируемая с квадратом функция Ф ( C s '( х — х , )) и параметр C s (коэффициент размытости) удовлетворяют некоторым условиям сходимости [3].

  Новые непараметрические оценки кривой регрессии. В качестве непараметрической функции регрессии предлагается класс статистик:

  
  

  lim С ;'( Ф , ( С ;'( х — х , )) + s ^rc

  ^+Ф 2 ^{( C}s' ⁽ х ^— х ))) = ^{5 ( x —} x ),

  
  
  
  

  c;¹ J (ф,( c ;'( х — х , )) +Ф 2 ( c ;'( х — х , ))) dx = 1. (7) Q( x )

  Если ( x ,... , х_п ) с R n , то непараметрическая оценка кривой регрессии (5) принимает вид:

  
  

  У* ⁽ x ) =

  
  

  V"¹ _ I х — х, 1_ I х — х, / У,- ф> — ф₂ — 1                    2

  - =1        V ^Cs ) V ^Cs

  
  

  ■^ I х — х ,. | _ I х / Ф> ---- Ф₂ -

  -=1      V ^Cs ) V

  
  

  —

  
  

  х а,

  
  
  
  

  sn

  z у п |Ф 1 ^х

  
  

  —

  
  

  С s

  
  

  У s ( x ) ₌ ±С ^ к_А_ ^s     sn

  zп |ф 1 I х

  i =1 j =1 v v

  
  

  С s

  
  

  х, I I х — х, II +Ф₂ ----^L

  ^{1      2 1} С ¹

  s -T---- z^V    s Л . (8)

  
  

  _—

  
  

  С s

  
  

  х, I I х — х, +Ф₂ ----^L

  I       ² 1 с

  s ) V s

  
  

  где функции Ф 1 ( C_s *( х — х , )), Ф ₂( C_s *( х — х , )) и параметр C s также удовлетворяют условиям сходимости [3] и свойству

  C s ¹ J Ф , ( C s ' ( х — х , )) Ф 2 ( С — ' ( х — х , ))dx = 1. (3) Q( x )

  
  

  В случае, когда ( x , ..., х_п ) с R n , непараметрическая оценка кривой регрессии (2) принимает вид

  
  

  sn

  Z У - П Ф 1 I x

  y s ( X ) = '= 1     j = 1   /

  
  

  — x ' , | I x, — x'-

  J---j Ф, - j---j

  C I ²1 C

  s ) V s

  
  

  sn

  ЕП ф . j i =1 j =1       I ^Cs

  
  

  x ' - I I x, — x'-

  -j Ф, - j—j

  I ² 1 C

  ) I ^s

  
  

  .

  
  
  
  

  Возможный вид функций Ф 1 ( - ), Ф 2 ( - ) представлен на рис. 1.

  Также может быть введена оценка следующего вида:

  
  

  s

  Z у |Ф 1 p

  У s ( X ) ⁼

  ^s

  х

  I ^Фг

  , =1 V V

  
  

  ^{х —} х | _{+ ф} I ^{х — х} i с J ² 1 с ss

  
  

  ^,

  
  

  — х, I I х — х, +Ф₂

  с I ²1 С

  s ) V s

  
  
  
  

  где интегрируемые с квадратом, ограниченные, четные, дельтообразные функции Ф 1 ( C s ¹ ( х — х , ) ) , Ф ₂ ( С ^— ( х — х , )) и параметр C_s (коэффициент размытости) удовлетворяют условиям сходимости:

  
  

  Непараметрические оценки функции регрессии имеют непосредственное отношение к задаче идентификации дискретно-непрерывных процессов по наблюдениям «входных–выходных» переменных. При этом выборочное пространство наблюдения соответствующих переменных может иметь некоторые особенности, в частности, сгущения, пустоты, разреженности.

  Для непараметрических оценок функции регрессии y_s ( x ) (2) и y_s ( x ) (5) имеют место следующие теоремы.

  Теорема 1. Пусть у ( x ) дважды дифференцируема и с вероятностью 1 p ( x ) >  0 , V x g Q ( x ), а функции Ф 1 ( C s '( х — х , )), Ф₂( C s '( х — х , )) и параметр размытости C_s удовлетворяют условию сходимости (3), тогда:

  lim M {( у ( x ) — y_s ( x ))²} = 0, V x gQ( x ). s ^rc

  Теорема 2. Пусть у ( x ) дважды дифференцируема и с вероятностью 1 p ( x ) >  0 , V x g Q ( x ), а функции Ф 1 ( C s '( х — х , )), Ф₂( C s '( х — х , )) и параметр размытости C_s удовлетворяют условиям сходимости (6) и (7), тогда:

  lim M {( у ( x ) — у s ( x ))²} = 0,

  s ^rc

  
  

  V x g Q ( x ) .

  
  

  ф I х-х ¹ V C s

  

  —

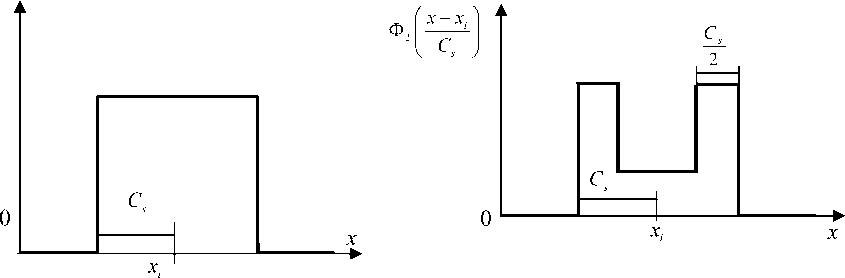
  С s

  Рис. 1. Вид функций Ф 1I —

  х , I I   х — х,

  и Ф

  
  

  I ²1 С

  ss

  
  

При доказательстве теорем использованы приемы, предложенные в [1; 4]. Более подробные доказательства приведены в [5; 6].

Исследование непараметрических оценок методом статистического моделирования. В процессе исследований использовалась истинная зависимость вида у ( x 1 ,x 2 ) = x 12 + ^^x2 + 2 x 1 x ₂ + h , где h - уровень помех, распределенных по нормальному закону с нулевым математическим ожиданием и ограниченной дисперсией, а значения ( x ₁, x ₂ ) генерировались из интервала [0, 4] таким образом, что стохастически зависимые переменные х 1 и х 2 образуют «трубчатый» процесс в выборочном пространстве ( у , x ₁ , x ₂ ) . Зависимость у ( x ₁, x ₂) необходима для получения выборочных данных, но при восстановлении регрессии информация о ее параметрической структуре считается неизвестной. Эксперименты проводились при различных объемах выборок «входных–выходных» переменных s , с различным уровнем помех h . Для восстановления у ( x ₁, x ₂) использовались непараметрические оценки кривой регрессии у _s ( x ₁, x ₂) вида (4), где n = 2, и у s ( x 1 , x ₂) вида (8), где n = 2. При построении непараметрических оценок функции регрессии использовались функции Ф 1 ( - ) и Ф ₂( - ), приведенные на рис. 1. Параметры размытости С_s выбирались путем минимизации критерия оптимизации:

1 ^s

w( Cs ) = ~ Е ( Уj — ys ( x1j, x2j )) ^ min , s j=1                                     s рессии уs (x1, x2) вида (8) более эффективна на данной выборке, чем оценка уs(x1,x2) вида (9).

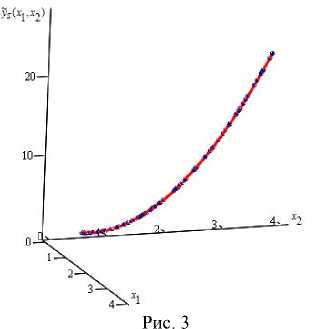
На рис. 3 график оценки кривой регрессии у_s ( x 1 , x ₂) представлен линией, исходная выборка процесса – точками. Объем выборки s = 60 точек, на интервалах [0,5; 2,1], [2,3; 2,7], [2,8; 2,9], [3,4; 3,5] и [3,7; 3,8] присутствуют сгущения, на интервалах [3; 3,3], [3,6; 3,7] и [3,9; 4] имеются разреженности, и на интервалах [2,1; 2,3], [2,7; 2,8], [2,9; 3], [3,3; 3,4] и [3,8; 3,9] отсутствуют элементы выборки. Уровень помех h = 0 %. Значения параметров размытости функций Ф 1 ( - ) и Ф ₂( - ), соответственно, C s 1 = 0,13 и C s ₂ = 0,18. Ошибки аппроксимации w_s = 0,03, w s = 0,12 . Таким образом, новая оценка кривой регрессии у_s ( x 1 , x ₂) вида (8) более эффективна на данной выборке, чем оценка у_s ( x ₁, x ₂) вида (9).

где ys(x1

x n ) =

sп

Е y H t i =1       j =1

x j

—

xⁱ j

С s

sп

ЕП Ф 1

i =1 j =1

, п = 2,

либо y_s ( x 1 , x ₂) вида (4), либо у_s ( x 1 , x ₂) вида (8).

В качестве точности аппроксимации использовалась квадратичная ошибка. Для оценки кривой регрессии у_s ( x ₁, x ₂) вида (9) ошибку обозначим как w_s , для оценки у _s ( x ₁, x ₂) вида (4) – как w _s , для оценки у_s ( x 1 , x ₂) вида (8) - как w_s .

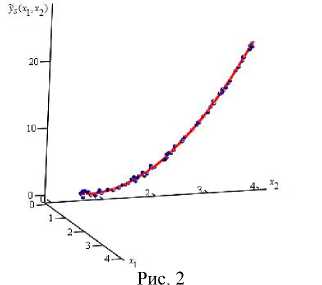
На рис. 2 график оценки кривой регрессии у_s ( x 1 , x ₂) представлен линией, исходная выборка процесса – точками. Объем выборки s = 80 точек, на интервалах [0,5; 1], [1,7; 2,1], [2,4; 2,8], [3,4; 3,6] и [3,9; 4] присутствуют сгущения, на интервалах [1; 1,7], [2,9; 3,3] и [3,7; 3,8] имеются разреженности, и на интервалах [2,1; 2,4], [2,8; 2,9], [3,3; 3,4] и [3,8; 3,9] отсутствуют элементы выборки. Уровень помех h = 10 %. Значения параметров размытости функций Ф 1 () и Ф ₂( - ), соответственно, C s 1 = 0,11 и C s ₂ = 0,14. Ошибки аппроксимации w_s = 0,05, w s = 0,15. Таким образом, новая оценка кривой рег

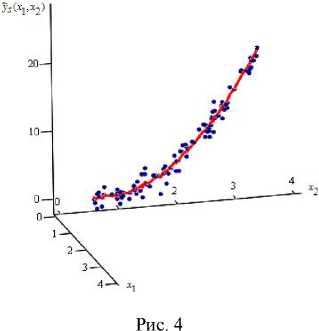
На рис. 4 график оценки кривой регрессии у_s ( x 1 , x ₂) представлен линией, исходная выборка процесса – точками. Объем выборки s = 100 точек, на интервалах [0,5; 2], [2,7; 3,1] и [3,4; 3,6] присутствуют сгущения, на интервалах [2,1; 2,6] и [3,1; 3,2] имеются разреженности, и на интервалах [2,6; 2,7] и [3,3; 3,4] отсутствуют элементы выборки. Уровень помех h = 25 %. Значения параметров размытости функций Ф 1 ( ) и Ф ₂( - ), соответственно, C s 1 = 0,07 и C s ₂ = 0,08. Ошибки аппроксимации i w_s = 0,08, w s = 0,19. Таким образом, новая оценка кривой регрессии у_s ( x 1 , x ₂)

вида (8) более эффективна на данной выборке, чем оценка у_s ( x ₁, x ₂) вида (9).

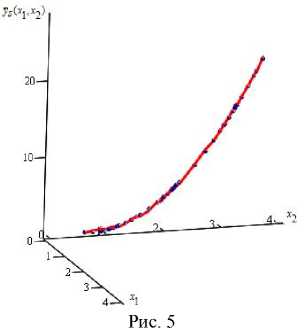
На рис. 5 график оценки кривой регрессии у _s ( x ₁, x ₂) представлен линией, исходная выборка процесса – точками. Объем выборки s = 50 точек, на интервалах [1; 1,3], [2,1; 2,5] и [3,4; 3,5] присутствуют сгущения, на интервалах [0,6; 1], [1,3; 2,1], [2,9; 3,4] и [3,6; 4] имеются разреженности, и на интервалах [2,5; 2,7] и [2,7; 2,9] отсутствуют элементы выборки. Уровень помех h = 0 %. Значения параметров размытости функций Ф 1 () и Ф ₂( - ), соответственно, C s 1 = 0,25 и C s ₂ = 0,29. Ошибки аппроксимации w s = 0,06, w s = 0,17 . Таким образом, новая оценка кривой регрессии у _s ( x ₁, x ₂) вида (4) более эффективна на данной выборке, чем оценка у_s ( x ₁, x ₂) вида (9).

На рис. 6 график оценки кривой регрессии уs(x1,x2) представлен линией, исходная выборка процесса – точками. Объем выборки s = 90 точек, на интервалах [2,9; 3,1] и [3,2; 3,3] присутствуют сгущения, на интервалах [0,7; 1,7], [1,8; 2,9] и [3,3; 4] имеются разреженности, и на интервалах [1,7; 1,8] и [3,1; 3,2] отсутствуют элементы выборки. Уровень помех h = 20 %. Значения параметров размытости функций Ф1() и Ф2(-), соответственно, Cs 1 = 0,09 и Cs 2 = 0,08. Ошибки аппроксимации ws = 0,1, ws = 0,22 . Таким образом, новая оценка кривой рег- рессии уs(x1, x2) вида (4) более эффективна на данной выборке, чем оценка уs(x1,x2) вида (9).

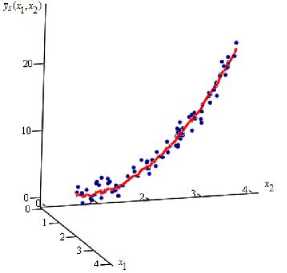
Рис. 6

На рис. 7 график оценки кривой регрессии у _s ( x ₁, x ₂) представлен линией, исходная выборка процесса – точками. Объем выборки s = 120 точек, на интервалах [0,6; 1,5] и [2,3; 3] присутствуют сгущения, на интервалах [1,5; 2,3], [3; 3,4], [3,5; 3,7] и [3,8; 3,9] имеются разреженности, и на интервалах [3,4; 3,5] и [3,7; 3,8] отсутствуют элементы выборки. Уровень помех h = 8 %. Значения параметров размытости функций Ф 1 ( ) и Ф ₂( - ), соответственно, C s 1 = 0,05 и C s ₂ = 0,05. Ошибки аппроксимации w s = 0,09, w_s = 0,2 . Таким образом, новая оценка кривой регрессии у _s ( x ₁, x ₂) вида (4) более эффективна на данной выборке, чем оценка у_s ( x ₁, x ₂) вида (9).

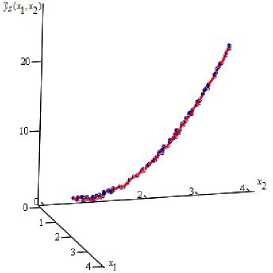
Рис. 7

Если (x1,...,x5)еR5, использовалась истинная зависимость вида y (x1,..., x5) = x12 + ^х 2 + 5sin( x 3) --3 lg(x4) + x5 + h , где h - уровень помех, распределенных по нормальному закону с нулевым математическим ожиданием и ограниченной дисперсией, а значения (x1,...,x5) генерировались из интервала [0, 4] таким образом, что стохастически зависимые переменные x1,...,x5 образуют «трубчатый» процесс в выборочном пространстве (у, x1,..., x5) . Зависимость y(x1,...,x5) необходима для получения выборочных данных, но при восстановлении регрессии информация о ее параметрической структуре считается неиз- вестной. Эксперименты проводились при различных объемах выборок «входных–выходных» переменных s, с различным уровнем помех h. Для восстановления y(x1,...,x5) использовались непараметрические оценки кривой регрессии уs (x1,...,x5) вида (4), где n = 5, и ys(x1,...,x5) вида (8), где n = 5. При построении непараметрических оценок функции регрессии использовались функции Φ1(⋅) и Φ2(⋅) , приведенные на рис. 1. Параметры размытости Сs выбирались путем минимизации критерия оптимизации:

1 ^s

w(Сs) = ∑(yj-ys(x1j,...,x5j))2 →min, s j =1 Сs где ys(x1,...,x5) вида (9), п = 5, либо уs(x1,...,x5) вида (4), либо уs(x„...,x5) вида (8).

В качестве точности аппроксимации использовалась квадратичная ошибка. Для оценки кривой регрессии y_s ( x ₁,..., x ₅) вида (9) ошибку обозначим как w_s , для оценки у _s ( x ₁,..., x ₅) вида (4) – как w _s , для оценки у s ( x 1 ,..., x ₅) вида (8) - как w s (см. таблицу).

Таким образом, при восстановлении функции регрессии по результатам экспериментальных данных в выборочном пространстве наблюдений могут иметь место сгущения, разреженности, пропуски данных. В этом случае классические непараметрические оценки восстановления стохастической зависимости типа (9) могут оказаться недостаточно эффективными. Предложен прием формирования ядерных функций некоторым специальным образом (рис. 1). Для новых непараметрических оценок функции регрессии доказаны соответствующие теоремы сходимости.

Проведение численных исследований показывает более высокую эффективность непараметрических оценок функции регрессии у _s ( x ₁,..., x_п ) вида (4) и у s ( x 1 ,..., х п ) вида (8). При использовании функций (4) и (5) квадратичная ошибка в среднем уменьшается в два раза. Следует обратить внимание, что исследование непараметрических оценок проводилось для процессов «трубчатой» структуры.