Об эффекте усиления при возбуждении и регистрации параметрических эхо-сигналов

Настоящая работа посвящена эффекту усиления, присущему т. н. параметрическому эхо-сигналу — нестационарному отклику физической системы на внешнее возбуждение двумя радиочастотными импульсами, когда второй (параметрический) импульс подается на несущей частоте 2 ω , удвоенной по отношению к несущей частоте ω первого (резонансного) импульса. Будучи во многом сходным с обычным откликом в последовательности ω— ω [1], параметрическое эхо обладает рядом особенностей, благоприятствующих его использованию в устройствах обработки информации [2, 3].

Данное явление наблюдается в разных объектах (в системах ядерных спинов [4], на акустических модах [5]), но основные свойства сигнала всюду одинаковы. Далее для определенности мы будем рассматривать эхо на собственных магнитоупругих колебаниях монокристаллических пластин бората железа — материала, в котором при комнатной температуре регистрируется интенсивный отклик с относительно большими временами релаксации [6, 7].

ПАРАМЕТРИЧЕСКОЕ УСИЛЕНИЕ ЭХО-СИГНАЛОВ

Временнáя диаграмма импульсной последовательности и возбуждаемых ею откликов физической системы приведена на рис. 1. Резонансный импульс (импульс 1 на рис. 1, а) возбуждает в образце магнитоупругие колебания с частотами, расположенными вблизи ω в диапазоне ~1 τω . В момент его окончания начинается расфазировка отдельных мод, и, после того как их фазы распреде- обработки информации на основе явления эха.

ляются в интервале (0, 2 π ), исчезает сигнал индукции (кривая 3 на рис. 1, а). Эволюция отдельных собственных колебаний при этом однако не прекращается, и они продолжают спадать, как показывает кривая 1 на рис. 1, б, с характерным временем затухания звука τ _s .

Во время действия параметрического импульса (импульс 2 на рис. 1, а) за счет модуляции скорости звука развивается параметрический процесс. В зависимости от фазы собственное колебание, имеющее к моменту прихода параметрического импульса амплитуду m , может быть усилено или ослаблено, причем усиление пропорционально exp( λτ _{2 ω} ) , а ослабление — exp( - λτ _{2 ω} ) ( λ — параметр, зависящий от свойств вещества и интенсивности параметрического импульса) [2, 7].

Раскладывая произвольную гармонику с фазой ϕ на ослабляемую и усиливаемую компоненты, для ее амплитуды после окончания действия параметри ческого импульса нетрудно пол учить m ′ = m exp(2 λτ _{2 ω} )cos² ϕ + exp( - 2 λτ _{2 ω} )sin² ϕ (система координат выбрана так, чтобы усиливалась x -составляющая). Поскольку условием усиления является m ′ m > 1 , усиливаться будут моды, на фазы которых наложено ограничение cos² ϕ > > ( k + 1) ^{- 1} , где k = exp(2 λτ _{2 ω} ) . Для реальных условий (по данным работ [6, 7]) оценка λ составляет ~ 10⁶ с^–1. Легко видеть, что даже при небольшой длительности второго импульса τ _{2 ω} ≈ 1 мкс из всей совокупности гармоник усиливается уже около 70 %.

Увеличение амплитуды или длительности параметрического воздействия приводит к быстрому нарастанию количества усиливаемых мод, большей также становится величина m ′ m в отдельной моде.

t 12 t 12

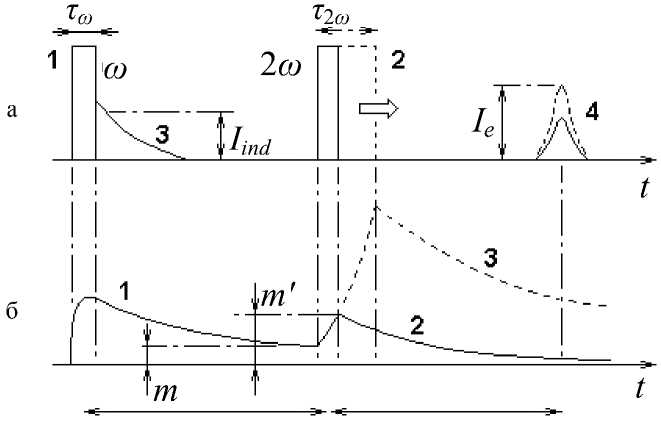
Рис. 1. Импульсная последовательность и реакция физической системы на ее воздействие.

а — временная диаграмма поступающих импульсов: 1 — резонансный импульс на частоте го , 2 — параметрический импульс на частоте 2 го и регистрируемых откликов: 3 — сигнал индукции, 4 — сигнал эха. Стрелкой показано увеличение длительности параметрического импульса.

б — поведение отдельной моды, принимающей участие в образовании откликов: 1 — спад магнитоупругих колебаний после резонансного импульса; 2 — спад магнитоупругих колебаний, усиленных коротким параметрическим импульсом; 3 — спад магнитоупругих колебаний, усиленных длинным параметрическим импульсом

Последнее обстоятельство отражено на рис. 1, б, где показано, как при увеличении т_{2 т} растет m' . Таким образом, можно утверждать, что уже на этапе возбуждения нестационарных откликов (то есть во время действия импульсной последовательности) в параметрической системе проявляется усилительный механизм.

Сигнал эха является результатом сложения всех мод, фазы которых так преобразуются параметрическим импульсом, что по прошествии времени 2 t ₁₂ после резонансного импульса происходит их "фокусировка" [2]. Следовательно, по своей природе параметрическое эхо является сигналом усиленным. Это однако не означает, что оно всегда превосходит входной сигнал, т. к. релаксация уменьшает амплитуды участвующих в формировании эха гармоник (рис. 1, б).

Будем считать, что возбуждение магнитоупругих колебаний линейно по резонансному воздействию, как это предполагается моделью, рассмотренной в [7]. Тогда обратное воздействие отклика наводит в приемной системе напряжение, находящееся в таком же отношении с напряжением, наведенным сразу после резонансного импульса, в каком амплитуда суммарных магнитоупругих колебаний в момент формирования эха находится с амплитудой магнитоупругих колебаний в момент окончания резонансного импульса. Это означает, что отношение сигнала эха Ie к сигналу 10, наводимому начальными колебаниями, может быть принято в качестве некоторого коэффициента преобразования входного сигнала, отражающего соответствующее соотношение для магнитоупругих колебаний. В том случае, если оно превышает единицу, данный коэффициент естественно назвать усилением. Отметим, что, строго говоря, 10 не является амплитудой сигнала индукции Ind, т. к. по условиям эксперимента Iind всегда измеряется с некоторой задержкой относительно окончания резонансного импульса.

Воспользовавшись строгим выражением для сигнала эха [7], запишем коэффициент полного

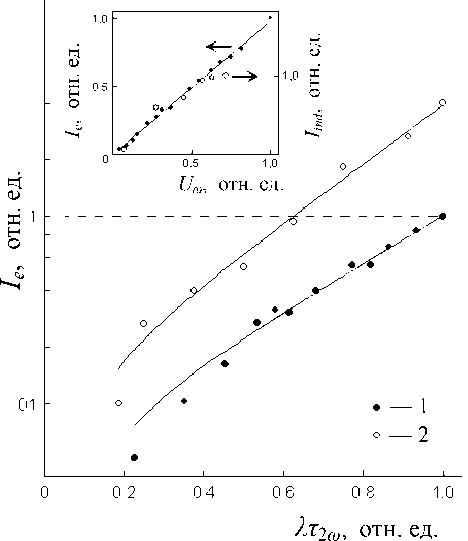
Рис. 2. Зависимости относительной амплитуды эхо-сигналов от интенсивности/длительности параметрических импульсов.

1 — последовательность ω —2 ω . 2 — последовательность ω —2 ω —2 ω : зависимость амплитуды дополнительного эха от второго параметрического импульса при относительной интенсивно-сти/длительности первого параметрического импульса λτ _{2 ω} = 1 . Горизонтальным пунктиром обозначена линия, на которой амплитуды первого и дополнительного эхо-сигналов становятся равными.

На вставке — зависимости амплитуд эха ( I _e ) и индукции ( I _ind ) от амплитуды резонансного импульса

2 t преобразования: K = I_eI ₀ = exp( - ¹² ) sh( λτ _{2 ω} ) . p                    τ _s

Два сомножителя в этом выражении описывают два основных фактора, определяющих амплитуду эха: экспоненциальное затухание каждой отдельной моды магнитоупругих колебаний (первый сомножитель) и собственно параметрическое усиление (второй сомножитель). Видно, что для принятой выше оценки λ , характерного значения τ _s ≈

≈ 20 мкс и τ _{2 ω} ≈ 1–2 мкс эхо является усиленным, т. е. превосходит по амплитуде начальные колебания при t ₁₂ ≈ 1–10 мкс.

На практике трудно наблюдать сигнал при столь малых задержках между импульсами в силу существования "мертвого времени" приемной системы и достаточно большой длительности индукции, но ясно, что в принципе на этапе регистрации может быть обнаружен усиленный отклик. Увеличение τ _{2 ω} по ряду причин часто бывает не вполне удобно, но если оно допустимо, интервал приема эха с K_p >  1 расширяется.

Дополнительную возможность усиления дает многократное параметрическое воздействие. Подавая, например, еще один импульс на удвоенной частоте спустя короткое время после формирования эхо-сигнала (последовательность ω— 2ω—2ω), можно получить второе эхо, большее по амплитуде, чем первое. При использовании данной методики маскирующие сигналы уже отсутствуют, и задержку можно сделать достаточно малой. Начальным сигналом здесь является первое эхо, амплитуду которого легко измерить и, следовательно, вычислить Kp . Очевидно, что если на образец поступит серия из N одинаковых дополнительных параметрических импульсов с одинаковыми интервалами, общее усиление эхо-сигнала N достигнет KpN .

РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ

Эксперимент выполнялся на установке, схема которой приведена в [2]. Длительность импульсов составляла порядка нескольких микросекунд, задержки — порядка десятков микросекунд, ω /2 π ≈ 70 МГц. Результаты эксперимента приведены на рис. 2. В двухимпульсной последовательности получено быстрое нарастание амплитуды эхо-сигнала с увеличением относительной "площади" параметрического импульса λτ 2ω .

Последовательность типа ω —2 ω —2 ω дает второй (дополнительный) сигнал эха, возрастающий с увеличением "площади" второго параметрического импульса. Обе кривые на рис. 2 описываются гиперболическим синусом (сплошные линии) с близким соответствием подгоночного параметра сделанным выше оценкам.

Очевидно, что в последовательности типа ω— 2ω—2ω зависимость амплитуды дополнительного эхо-сигнала от "площади" начинается, как и в двухимпульсной последовательности, от нуля и в некотором интервале значений λτ2ω не превышает амплитуды эха первичного. Лишь с определенного момента (при λτ2ω ≈ 0.6 , рис. 2) наблюдается превышение амплитуды второго сигнала над первым, когда дополнительное эхо, собственно, и должно считаться усиленным. Из рис. 2 видно также, что максимальное достигнутое Kp , равное отношению амплитуд дополнительного и первого эха, приблизительно равно четырем.

На вставке рис. 2 демонстрируется линейность откликов по резонансному воздействию, указывающая на допустимость использования развитого выше подхода. Таким образом, эксперимент подтверждает представление о параметрическом эхо-сигнале как об отклике, природа которого принципиально связана с усилением.

ВЫВОДЫ

В работе установлено, что нестационарные отклики физической системы, формирующиеся по параметрическому механизму, должны рассматриваться как усиленные. Показано, что в ряде случаев за счет поступления в систему энергии из параметрических импульсов они могут превосходить входной сигнал, возбужденный импульсом резонансным. На эксперименте достигнуто значительное (в несколько раз) увеличение эхо-сигнала. Данное свойство может быть использовано в эхо-процессорах — устройствах обработки импульсной информации на основе нестационарных откликов, для которых остро стоит проблема поднятия чувствительности.

Учет изученных в работе эффектов также может оказаться полезным при аналитических исследованиях различных физических систем (ядерных спинов, акустических мод и т. д.) и материалов с помощью импульсных методов.