Об эффективности алгоритмов Рейдера-Винограда

Хорошо известно [1], что для некоторых простых p = N существуют быстрые алгоритмы дискретного преобразования Фурье (БА ДПФ) с минимальным числом умножений. Синтез таких алгоритмов, как показал Рейдер [2]), сводится к эффективному вычислению циклической свертки длины ( p - 1 ) . Вычисление свертки эквивалентно параллельному вычислению произведений некоторых полиномов по модулям циклотомических полиномов P 1 ( t ) , ..., P d ( t ) , где P ( t ) ... P d ( t ) = t p ^{- 1} - 1.

Полуэвристическое нахождение формул «экономного» умножения в полиномиальных кольцах ( mod P j ( t ) ) является основой метода Винограда [3],[4], в рамках которого получены абсолютные нижние оценки мультипликативной сложности БА ДПФ и лишь для некоторых небольших простых чисел p синтезированы БА с хорошими вычислительными характеристиками [5]. Способ сведения ДПФ с простым числом отсчетов к циклической свертке, использующий цикличность мультипликативной группы простого конечного поля, предложен Ч.Рейдером в 1968 г. Без какой-либо общей теории быстрые алгоритмы коротких сверток были впервые описаны в [3]. В 1976 г. Ш.Виноград [4] предложил метод построения алгоритмов коротких сверток и доказал теоремы о сложности рассмотренных алгоритмов свертки для полей комплексных и вещественных чисел. К сожалению, некритическое прочтение работ Ш.Винограда сформировало у определенной части пользователей представление об оптимальности, неулучшаемости БА Винограда и их существовании для всех простых р . Сам Ш. Виноград показал зависимость сложности вычисления свертки от арифметических свойств поля, в котором производятся вычисления. В настоящее время оптимальные алгоритмы ДПФ известны для простых p = 2, 3, 5, 7, 11, 13, 17, 19 (см., например, [5]).

В данной статье показывается, что уже традиционное сведение вычисления ДПФ простой длины p к свертке длины ( p - 1 ) = 5 , в случае, когда 5 «плохо» факторизуется, может приводить к «быстрым» алгоритмам, сложность которых выше тривиального (непосредственного) вычисления ДПФ.

1.    Некоторые примеры

Пример 1. Рассмотрим вычисление дискретной круговой свертки p-i

z(m) = (x*y)(m) = ^x(n) y(m-n)         (1)

n = 0

вещественных последовательностей с периодом p =47. Пусть M ( N ) и C ( N ) – мультипликативные сложности вычисления N -точечного ДПФ вещественного массива и N -точечной круговой свертки вещественных последовательностей, соответственно; C *( N ) - мультипликативная сложность вычисления свертки вещественной и комплексной последовательностей. Примем типичное для БА Рейдера-Винограда соглашение, что вычисление ДПФ комплексного массива требует в два раза больше умножений, чем вещественного [1]. Будем также считать, что умножение комплексных чисел реализуется посредством трех вещественных умножений.

• 1.    Вычисление 47-точечной свертки по стандартной спектральной схеме требует вычисления двух 47-точечных ДПФ вещественных массивов, одного (обратного) ДПФ комплексного массива и 3 • 47 = 141 вещественных умножений для реализации умножения 47 спектральных компонент. Таким образом, справедливо равенство:

• 2.    Вычисление 47-точечного ДПФ, согласно основной идее метода Рейдера, сводится к вычислению 46-точечной свертки вещественной с комплексной последовательностью значений базисных функций ДПФ, что предполагает, по крайней мере, вычисление двух 23-точечных сверток функций указанного вида. Поэтому из (2) следует

• 3.    Так как число 23 также простое, то вычисление 23-точечных сверток опять сводится к вычислению 23-точечных ДПФ и дополнительным умножениям спектральных компонент. Так как ДПФ подпоследовательностей значений базисных функций 47-точечного ДПФ могут быть выполнены заранее, то справедливо равенство

C ( 47 ) = 4 M ( 47 ) + 141.                       (2)

C ( 47 ) = 2 • 4 • C * ( 23 ) + 141.

C *( 23) = 3 M (23) + 3 • 23, откуда, с аналогичной аргументацией, получаем:

C ( 47 ) >

> 24 M ( 23 ) + 141 + 3 • 8 • 23 >  693 + 48 C * ( 11 ) >

> 693 + 48 ( 3 M ( 11 ) + 33 ) = 2277 + 144 C * ( 10 ) >  (3)

> 2277 + 288 C ( 5 ) .

Лучший из известных алгоритмов вычисления 5точечной свертки содержит 10 вещественных умножений [6]. Поэтому из (3) следует C ( 47 ) >  5157 . В то же время, прямой метод вычисления правой части равенств (1) для m = 0, ..., 46 требует 47 • 47 = 2209 умножений, то есть приблизительно в 2 раза меньше. Основными причинами парадоксального результата в рассмотренном выше примере является существование «достаточно длинной» цепочки простых чисел

Р1 = 5, p2 = 2Р1 +1 = 11, p3 = 2p2 +1 = 23, p 4 = 2 p 3 +1 = 47                              (4)

и практически безальтернативная необходимость вычисления свертки простой длины спектральными методами. Общий результат о «исключительных» простых числах p , для которых, по всей видимости, не существует удовлетворительных алгоритмов вычисления ДПФ и свертки длины p, описывается следующим утверждением.

Теорема 1. Пусть p ₀ - простое, d ₀ , … , d_k -такие натуральные числа, что p_{t + 1} = d_tp_t + 1 -также простые числа. Пусть w = dk. - d ₀ p ₀ . Тогда справедливо неравенство

^M ( pk + 1 ) > -Л—Л ( ² • ^{4 k} - 1 ) . max { d j }

0 < j <  k

Доказательство. Аргументация аналогична рассуждениям Примера 1. Для любого t = 1, ..., k справедливы неравенства:

^M ( p. + 1 ) = ^C * ( d t p t ) >  d t ^C * ( p. ) >  ⁴ dM ( p. )^{+ 3} p. .⁽⁶⁾

Кроме того, для t = 0 аналогично (6) имеем

M ( p ) = C • ( d 0 p 0 ) > d 0 C •( p 0 ) > 2 d 0 C ( p 0 ) .    (7)

Нижние оценки Винограда для C ( p ₀ ) имеют вид C ( p ₀ ) >  2 p ₀ - t , где T - число неприводимых многочленов P j ( z ) в разложении многочлена Рейдера [1]:

z p ^{0 - 1} - 1 = P 1 ( z ) . Pt ( z ) . (8)

Число T зависит от поля, над которым рассматривается разложение (8) (см., например [2]), но в любом случае т <  p ₀. Поэтому C ( p ₀ ) >  p ₀.

Утверждение теоремы получается редукцией неравенства (6) с учетом соотношений (7)-(8) и очевидного неравенства p_{t + 1} <  d_td_t 1 . d ₀ p ₀.

Действительно

^M ( p_k + 1 ) > ^{4 d} k ^M ( p_k ) ^{+ 3} p_k >

• > ⁴ d k ^M ( p_k ) ^{+ 3} d k - 1 - ^d 0 p 0 >

• > ⁴² d k d k - 1 ^M ( p_k - 1 )⁺

• ^{+ 4} • ³ d k d k - 2 . ^d 0 p 0 ^{+ 3 d} k - 1 . ^d 0 p 0 >

• > 4 ^k • 3 d k d k - 1 - d 1 M ( p ) +

• + 3 § 4 ¹ ( d k - , )^- 1 d k - d 0 p 0 >

• 5 = 0

• >              ( 2 • 4 ^k - 1 ) .

max { d j }

• 0 < j <  k

Проводимое ниже следствие дает достаточно грубые, но легко проверяемые неравенства, характеризующее «исключительные» простые числа, для которых, как и в Примере 1, последовательное применение метода Рейдера приводит к алгоритмам ДПФ (или свертки), мультипликативная сложность которых выше, чем при непосредственном вычислении соответствующих сумм.

Следствие 1. Пусть p ₀ - простое, d ₀, … , d_k -такие натуральные числа, что p _{t + 1} = d_tp_t + 1 - также простые числа.

Если справедливо неравенство

• 6 k 4-1 >  log 2 p_k + 1 ,                                 ⁽⁹⁾

то справедливо и неравенство

M ( p_k + 1 ) > 2 p ^+1 .                                (10)

Доказательство. Так как max{d,)< w, ,

• 0 < j < k^{v й} p 0 2 ^k

то

----( 2 • 4 ^k - 1 ) > p ₀2 ^k ( 2 • 4 ^k - 1 ) > 2 • 2 ^k • 4 ^k - 2 ^k . max { d } 0 < j < k ^L j ^J

Поэтому из неравенства

• 8 k > p2+1 + 2 k(11)

следует неравенство (5). Но log 2 ( p 2 + 1 + 2 ^k ) =

L 2k 1

= ^2log 2 p_k + 1 ⁺ log 2 I ¹ + — I <  ^2log 2 p_k + 1 ⁺T

I   pk+1 J откуда легко следует (6).

Аналогичное неравенство справедливо и для вычисления p -точечной свертки при «исключительных» простых p .

Следствие 2. Пусть p ₀ - простое, d ₀, … , d _k -такие натуральные числа, что p_{t +1} = d_tp_t + 1 - также простые числа, k >  4. Тогда, если справедливо неравенство

6 k + 5 ,                                                      ...

• —— >  log 2 p_k + 1 ,                         ⁽¹²⁾

то справедливо и неравенство

C ( p_k + 1 ) > pL-                                (13)

Доказательство. В силу неравенства

C ( p_k + i ) = 4 C ( Pk + i )⁺ Pk + i > ⁴ M ( Pk + i ) ,

Примера 1, доказательство неравенства (13) проводится аналогично доказательству неравенства (10) предыдущего следствия.

Пример 2. Пусть p 0 = 2 ; p_{t + 1} = d_tp_t + 1, где d о = 2 , d 1 = 2 , d 2 = 8, d 3 = d 4 = d 5 = d 6 = d 7 = 2. Тогда   p ₈ = 2879 - простое число, все p_t

( t = 0, ..., 7 ) также простые. Неравенство (12) в этом случае выполняется:

6 k ¹ 5 = 11,75 >  11,55 >  log₂2879.

2. О плотности исключительных простых чисел в натуральном ряду

Анализируя вышесказанное, автор считает возможным высказать предположение, что «плохих» простых чисел, которые порождают такие натуральные N , что для этих длин не существует эффективных алгоритмов вычисления ДПФ и свертки, бесконечно много, но встречаются они весьма редко. Первая часть предположения базируется исключительно на субъективном авторском мнении.

Гипотеза. Существует бесконечно много конечных множеств натуральных чисел d ₀ , … , d_k и таких простых p 0 , что числа p_{t + 1} = d_tp_{t + 1} также являются простыми, причем для p_{k + 1} выполняются неравенства (9)-(10) или (12)-(13) .

Вторая часть предположения (о редкости «плохих» простых) базируется на вполне определенных количественных результатах.

Определение. Если простое p таково, что число q = 2 p + 1 также простое, то число p называется простым числом Софи Жермен.

Простые числа (4) как раз и являются простыми Софи Жермен. Первыми такими простыми являются числа 2, 3, 5, 11, 23, 29, 41, 53, 83, 89, 113, 131. Конечно или бесконечно множество простых Софи Жермен в настоящее время неизвестно. Известна только гипотетическая асимптотическая оценка количества 5 ( N ) простых Софи Жермен, на превосходящих данного N :

5 ( N ) - 2 C ₂

N

( ln N ) ²

где C ₂ = 0,6601618158... - так называемая «константа простых близнецов». Оценка (14) достаточно хорошо согласуется с результатами численных экспериментов [10]-[12].

Разумеется, даже в случае справедливости оценки (14) нельзя утверждать бесконечность множества чисел, для которых справедлива Гипотеза (число q = 2p +1 может быть и простым, а для простого p, простого Софи Жермен, «хорошо» факторизуется число (p -1)). Простые числа q = 2p +1 для простых чисел p Софи Жермен можно охарактеризовать и так: число (q -1) имеет «аномально мало» простых делителей (всего два). Простые числа с аномально малым количеством делителей у числа (q -1) рассматривались в работе [7]. Косвенным подтверждением высказанного в Гипотезе предположения о редкости «исключительных» простых и «плохих» натуральных, ими порожденных, явилась бы информация о количестве «обобщенных простых Софи Жермен», при которых q = kp + 1 также простое при некотором четном k и количественная информация о «редкости» простых q с «аномально малым» числом простых делителей у числа (q -1).

Обозначим N ( p <  x ; A ) число простых p <  x , для которых выполняется условие A . Справедливы следующие утверждения [7],[8].

Теорема 2. Для четного k,2 < k < x справедливо неравенство:

N ( p <  x ; p - 1 = kq , q - простое ) = O

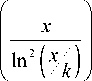
Пусть далее v ( n ) - число различных простых делителей числа n . Известно ([8], c.188), что «нормальное» число простых делителей числа n равно lnln n , то есть, за исключением o ( x ) значений n , n <  x , выполняются неравенства

(1 - £)lnlnn < v(n) < (1 + £)lnlnn .

Следующая теорема показывает, что числа ( p - 1 ) ведут себя так же, как и все натуральные.

Теорема 3. Для любого £ >0 выполняется асимптотическое равенство