Об эффективности анализа и распознавания изображений методом главных компонент и линейным дискриминантным анализом

Одной из важнейших проблем измерения и обработки информации является проблема распознавания объектов. Автоматизация процесса распознавания объектов ведёт к ускорению работы систем измерения и обработки данных и повышению их эффективности. Большой интерес к данной проблеме в различных областях науки и техники обусловлен многообразием прикладных задач, в которых используются либо сами изображения, либо результат их обработки. Необходимость в обработке и анализе изображений возникает не только при распознавании объектов, но и при изучении природных ресурсов Земли из космоса, управлении движущимися объектами, количественной оценке параметров объектов и т. п.

При анализе и распознавании изображений отдельное изображение представляется в виде вектора признаков, каждый из которых отражает значение яркости одного пикселя. Таким образом, если изображение описывается матрицей пикселей a х b , размерность вектора равна произведению a на b . Поскольку вектор каждого изображения имеет достаточно большую размерность, задача обработки большого количества изображений является нетривиальной.

Большинство систем анализа изображений основывается на методах построения пространства признаков меньшей размерности. Задача снижения размерности важна еще и потому, что сложность большинства алгоритмов экспоненциально возрастает с увеличением размерности изображений, а практическая реализация таких алгоритмов требует мощных вычислительных средств. Одним из широко распространенных методов сокращения размерности изображений является метод главных компонент (МГК). В настоящее время для решения задачи поиска и распознавания лиц предлагаются множество алгоритмов, использующих МГК.

Идея использования главных компонент для представления изображений лиц описывается в работе [1]. Любой набор изображений лиц может быть приблизительно восстановлен с помощью небольшого набора главных компонент и весовых коэффициентов для каждого изображения. Поскольку главные компоненты имеют ту же самую размерность, что и исходные изображения лиц, их часто называют «собственными лицами» или «собственными изображениями». Весовые коэффициенты, описывающие каждое изображение, будем называть главными факторами. Изображение хранится как набор главных факторов в базе данных в форме, которая может использоваться в качестве ключа поиска. В этом случае каждый фактор отображает не единичный пиксель, а группу пикселей, которые могут быть представлены в виде изображений (собственных лиц). Когда главные компоненты определяются на основе всех изображений, они создают полное пространство базисных векторов, то есть необходимая точность описания любого изображения достигается путем увеличения количества главных компонент. Если в качестве главных компонент используются все собственные вектора, то изображение восстанавливается точно.

Линейный дискриминантный анализ является мощной технологией распознавания лиц, преобразующей исходное пространство изображений в низкоразмерное пространство признаков, в котором изображения классов группируются вокруг их центров, а центры классов удаляются друг от друга настолько, насколько это возможно [2–4].

В работе [5] предложен подход, состоящий из двух шагов. На первом шаге используется метод главных компонент для сокращения размерности изображений. На втором шаге применяется ЛДА для преобразованных данных. Для вычисления главных компонент формируется учебная выборка, состоящая из изображений, сгруппированных в классы. Изображения одного класса описывают лицо одного человека. Один класс может содержать десятки и даже сотни изображений одного лица.

Вычисление главных компонент сводится к задаче собственных значений больших матриц. Известно, что вычисление собственных значений для небольших матриц практически закрытая проблема. Однако в случае больших матриц задача перестает быть тривиальной.

Методы понижения порядка матриц (конденсации) являются эффективным средством нахождения собственных векторов больших матриц, так как целью конденсации является получение матрицы меньшего порядка, которая была бы подобна исходной матрице в том смысле, что собственные значения этих матриц в заданном диапазоне совпадали бы с заданной точностью. Различные схемы конденсации (частотно-динамическая конденсация [6], частотная конденсация [7], линейная конденсация [8]) были предложены для повышения точности решений. Метод линейной конденсации используется для получения решений в заданном интервале собственных значений. В данной работе для повышения точности линейной конденсации предлагается использовать процедуру блочной диагонализации матрицы.

Распознавание изображений на основе МГК и ЛДА

Метод, основанный на МГК и ЛДА, состоит из 2 шагов: сначала мы проецируем изображение лица из исходного пространства признаков в подпространство собственных лиц с помощью метода главных компонент, затем используем ЛДА, чтобы получить линейный классификатор. Допустим, существует набор изображений, каждое из которых описывается вектором x_i ( i = 1, 2, 3, …, m ), где m – число различных изображений в обучающем наборе. Размерность n вектора x_i равна числу пикселей изображения. Таким образом, все изображения могут быть представлены в виде матрицы, столбцы которой являются векторами x_i . Средний вектор обу-

1 m чающих изображений v = —V xi вычитается из каждого изображения в обучающем наборе. Та-mi ким образом, получается новое пространство X0 = |^х0 x0 — x® J, где x0 = xi - v.

Подход МГК плюс ЛДА можно рассматривать как линейное преобразование исходной пространства изображений в проекцию пространства главных компонент, то есть

Z = W T X 0 ,                                                                      (1)

где Z - p x m матрица главных компонент, W - n x p матрица преобразования.

Как известно, метод главных компонент является техникой снижения размерности, основанной на извлечении желаемого числа главных компонент из многомерных данных. Первая главная компонента представляет линейную комбинацию исходных признаков, которая имеет максимальную дисперсию, а n -я главная компонента является линейная комбинация с самой высокой дисперсией среди m - n + 1 главных компонент и ортогональной n - 1 первых главным компонентам.

Известно, что матрица X ⁰ может быть представлена в виде сингулярного разложения.

X 0 = U _pca ЛV ,                                                                (2)

где Upca (m x p) и Vpca (n x p ) - матрицы левых и правых собственных векторов X0, Л - диа- тональная матрица (p х p), диагональные элементы которой щ , П2, • -, Пp являются положительными собственными значениями матрицы X0 . Здесь p – ранг матрицы X0 .

Ключевым моментом МГК является вычисление матрицы главных компонент V _pca . Матрица главных компонент V _pca формируется из правых собственных векторов v _{0 i} , которым соответствуют наибольшие собственным значениям n i •

Матрица собственных векторов V _pca может определяться как

V T_ctt = Л ^- 1 U Tca X 0 .                                                                              (3)

Матрица левых собственных векторов U _pca образуется из собственных векторов уравнения

( A m -X I m ) Uo = 0,                                                                          (4)

где Im - единичная матрица с порядком m, u0i - собственный вектор, а Xi = n2 — собственное значение матрицы

A m = 1 ( X ⁰ ) ^T X ⁰. m

Обозначим средний вектор класса к как vк, а среднее значение всех изображений как v mk v к= - Z zi;

m , = 1

K    mk

_{ν =} 1       1      _z k .

K к m_k ^Z i

Здесь K – число классов, а m_k – число изображений лиц в классе k .

Матрица межклассовых различий A _b может быть вычислена как

K mk

A     Zzizk-vк)(zk-vк) .(5)

^m к = 1 i = 1

Матрица внутриклассовых различий определяется как

1 ^K

Ab =—Zmk (vк-v)(vк-v) .

m _k

С помощью ЛДА ищется такое преобразование, которое максимизирует межклассовые и ми- нимизирует внутриклассовые различия

V dla = argmax

V e R n ^{х r}

V ^T A b V

V T A _m V

.

Чтобы определить V _lda , решается задача собственных значений

( A _b -X A „ ) v ld ^a = 0.                                                                        (8)

Решение уравнения (8) представляет обобщенную задачу собственных значений.

Комбинируя МГК и ЛДА, мы получаем матрицу линейного преобразования, которая проецирует изображение сначала в подпространство собственных лиц Z , а потом в пространство классификации

W = V,. V

lda pca , где Vlda – линейное дискриминантное преобразование в пространстве главных факторов. После такого линейного преобразования распознавание изображения выполняется в пространстве дискриминантных факторов с использованием различных метрик, например, Евклидова расстояния.

Вычисление главных компонент больших наборов данных

Разработка систем распознавания лица требует компромисса между универсальностью, требуемой точностью и быстродействием. Когда задача распознавания лиц ограничена небольшим набором людей, достаточно небольшого количества собственных лиц, чтобы описать интересующие лица. Однако если систему нужно обучить новым лицам или представить в ней значи- тельное число людей, потребуется больший набор собственных лиц. В этом случае необходимо решить проблему собственных значений для больших матриц.

Задача вычисления наибольших собственных значений уравнения (4) сводится к задаче нахождения наименьшего собственного значения уравнения

( I m — M A m ) V o = 0,                                                                         (10)

где m = 1/ X .

Мы делим вектор v0 на две части, а именно, вектор основных и вспомогательных перемен- ных. Вектор основных переменных содержит признаки, которые сохраняются при сокращении матрицы. Вектор вспомогательных переменных включает признаки, которые удаляются. В соответствии с таким делением уравнение (10) переписывается в разделенной форме следующим об- разом

I rr 0   f v o r 1      A rr i f — M

. 0 I _ss J I v o s [ A sr

A rs

^A ss

f v o r f I ^V0 s

= 0,

где индекс r относится к основным признакам, а индекс s – к вспомогательным признакам. Используя нижнее уравнение системы (11), можно определить связь вектора вспомогательных и основных переменных v0 s = M(l ss -MAss ) A sr v0 r • (12)

Путем подстановки вектора вспомогательных переменных (12) в уравнение (11) мы получаем

( I rr -m A rr + D rr ( m ) ) V 0 r = 0,

где D rr ^{(m) M} a rs ( ^M A ss  I ss ) A sr .

Сокращение матрицы Am осуществляется путем аппроксимации матрицы Drr (м) выраже- нием

* ^*

^D rr ^(m) ~ I rr - ^M A rr .

Коэффициенты подматриц A * _r и I r _r определяются из условия совпадения матриц D _rr ( м ) и

*

Irr-mArr в граничных значениях заданного диапазона собственных значений (M1, M2). Это соот ветствует линейной аппроксимации матрицы Drr (m) • В этом случае матрицы А* и Irr опреде- ляются по следующим формулам:

1 * п („        ^D rr ( M 1 ) - D rr ( M 2 ) .

I rr ^D rr ^(M 1 ) ^M 1                         ;

M l - M 2

ки в решении является то, что матрица D _rr ( ц ) аппроксимируется линейным матричным выражением. Ошибка аппроксимации матрицы D _rr ( ц ) определяется как

E rr ^(ц) = D rr ^{(ц) —} ( I rr - ^{ц А} rr ) .                                                                     ⁽¹⁸⁾

Значение коэффициента drr (ц) достигает бесконечности для ц = ц5, где ц5 - собственное значение матрицы A^. Таким образом, коэффициенты матрицы Еrr (ц) достигают бесконечно сти при ц = ц5.

Оценка максимальной величины ошибки собственных значений может быть получена на основе нормы матрицы Е rr ( ц ) . Чтобы получить такую оценку, вычтем из уравнения (13) уравнение (16), считая v_{0 r} = v 0 _r , в результате получается следующее уравнение

( Ац А r + E rr ( ц ) ) v o r = 0.                                                                        (19)

Оценка величины ошибки собственных значений может быть получена в виде

Ац< |a - ¹ E rr ( ц )| .                                                                                  (20)

Учитывая тот факт, что коэффициенты матрицы ошибок достигают максимального значения внутри диапазона ц1...ц ₂, середину диапазона ц m = ( ц1 +ц ₂)/2 можно использовать для оценки максимальной ошибки. Подставляя ц = ц m в соотношение (20), получим оценку максимальной ошибки собственных значений. Для ц 1 = 0 соотношение (20) будет иметь вид

Ац<

A - ¹ ( D rr ( ц m ) -^ m D rr ( ц 2 ) ц 2

Если ц5 (собственное значение матрицы A^) лежит в диапазоне ц1 ^ ц2, то Ац становится равным бесконечности, так как матрица ц Ass - Iss становится вырожденной. В качестве критерия, характеризующего величину Ац, можно использовать фактор ц5 /ц2 .

Метод линейной конденсации реализуется в форме алгоритма многоуровневой линейной конденсации, суть которого заключается в том, что признаки исключаются не все сразу, а группами. Алгоритм многоуровневой линейной конденсации включает пять шагов, которые описаны в работе [8]. Первый шаг представляет собой многоуровневую процедуру понижения порядка матриц, которая начинается с того, что все признаки сортируются в порядке убывания диагональных коэффициентов ковариационной матрицы A . На первом уровне выбирается группа признаков с минимальными диагональными коэффициентами a_ii . Блок удаляемых формируется из признаков с наименьшими диагональными коэффициентами. Решение об исключении выбранных признаков принимается при выполнении условия

Ц min >  k c ц 2^{. (22)} Здесь ц_тЬ - наименьшее собственное значение блока удаляемых переменных, k c называется фактором отсечения.

Таким образом, степень сжатия матриц уравнения (4) зависит от значений диагональных коэффициентов. Для повышения эффективности процедуры понижения порядка матриц предлагается использовать блочные вращения, диагонализирующие матричные блоки, лежащие на диагонали.

Процедура диагонализации выполняется до начала понижения порядка матриц. Пусть матрица A ^* разбита на f блоков

A ₁₁

^A 12  ""   ^A 1 f

^A f =

A 21

A 22

'" A 2 f

.^A f 1   ^A f 2   •"  ^A ff

Пусть имеется ортогональная матрица P _i , диагонализирующая матричный блок A _ii , т. е.

P T A * P i = L ii , где L ii - диагональная матрица.

Тогда вектор u ^pca

можно представить в виде

pca u0  =

P 1 0

P 2

u1tr ut2r

^ = Pu tr .

^P f J

tr l u f

Подставляя (24)

P ^T I _m P = I _m , получим

в

уравнение (4) и умножая справа на матрицу P ^T и учитывая, что

( A tr -X I _m ) U tr = 0, где A tr = P ^T A * P . С учетом блочного разбиения матрица A ^tr может быть представлена в виде

A ^tr

Σ 11

T

P ₂ A ₂₁ P ₁

P ^T f A f 1 P 1

T

P 1 A 12 P 2

Σ ₂₂

P ^T f A f 2 P 2

• -    P I T A 1 f ^P f

• -    P T ^A 2 f ^P f

Σ _ff

.

Нетрудно заметить, что ортогональная матрица P _i может быть получена из решения следующего уравнения

( A ,, -X 1 ₁ ) P = 0.

Экспериментальные исследования

В экспериментах используется подмножество базы данных FERET [9]. Подмножество состоит из 1731 изображения 121 человека в оттенках серого цвета. Каждый человек представлен в наборе минимум 10 образцами. Размер изображений 112 x 196 пикселей. Эти изображения охватывают широкий спектр вариаций освещения, выражений лиц, наклонов и поворотов головы. Предварительная обработка изображений не выполняется. Рис. 1 показывает некоторые примеры использованного подмножества.

Рис. 1. Некоторые образцы из базы данных FERET

Исследуется влияние точности вычисления главных компонент алгоритмом многоуровневой линейной конденсации на качество распознавания лиц. Для этого используется подмножество изображений из базы FERET, которое разделено на 2 набора данных: обучающий набор и тестовый набор. Обучающий набор состоит из 1089 образцов. Тестовый набор состоит из 642 образцов. Совпадений между двумя наборами нет.

Главные компоненты обучающего набора вычисляются с использованием метода линейной конденсации с различным значением фактора отсечения. Рассматриваются три вариации фактора отсечения: 1,5; 2 и 2,5. Точность главных компонент вычисляется по формуле εi = v*0i - v0i Il/llv0i , где v*0i – главные компоненты, вычисляемые алгоритмом линейной конден сации, а v0i – главные компоненты, полученные методом Хаусхолдера.

На рис. 2 показана зависимость ошибки главных компонент ( ε _i ) от их номера ( i ). Как видно из рисунка погрешность расчета достигает максимальных значений лишь для небольшого количества главных компонент. В то время как средняя погрешность главных компонент, как правило, на порядок меньше максимальных значений ошибки.

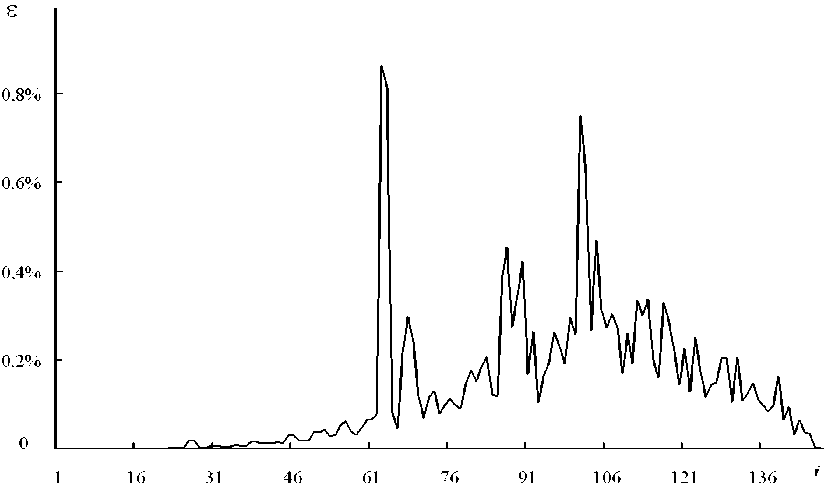
Рис. 2. Зависимость ошибки вычисления главных компонент от их номера

В таблице представляются максимальные значения ошибки расчета главных компонент при различных значениях фактора отсечения. Из таблицы видно, что чем больше значение фактора отсечения, тем меньше максимальная ошибка вычисления главных компонент.

Зависимость максимальной ошибки расчета главных компонент от фактора отсечения

Фактор отсечения	1,5	2	2,5
Ошибка расчета главных компонент	0,58	0,127	0,00862

Как видно из таблицы, наибольшая ошибка вычисления главных компонент достигается, когда значение фактора отсечения равно 1,5. Однако при значении фактора отсечения 2,5 величина ошибки уже незначительна.

Для оценки точности распознавания изображений используется тестовый набор, содержащий 642 изображения. В экспериментах для каждого обучающего набора вычисляются главные компоненты, которые используются при вычислении дискриминантных компонентов. Классификатор ближайшего центра класса используется для распознавания лиц. Этот классификатор исполь- зует среднее арифметическое всех изображений одного класса в качестве прототипа класса. Квадрат расстояния от x до класса i определяется по формуле di (x) = |x -vi||. Если расстояние между x и классом i минимально, то решением классификатора ближайшего центра класса является то, что x принадлежит классу i .

На рис. 3 представлена зависимость коэффициента распознавания изображений тестового набора K_test от числа дискриминантных компонент ( r ). Зависимости получены для 140 главных компонент, которые используются для вычисления дискриминантных компонент. Сплошная линия показывает результаты, полученные с использованием главных компонент, вычисленных методом Хаусхолдера. Коэффициенты распознавания, полученные при использовании главных компонент, вычисленных с помощью алгоритма линейной конденсации, изображены пунктирной линией (CF= 1,5), штриховой линией (CF=2), штрихпунктирной линией (CF = 2,5). Здесь CF (Cut-off Factor) – фактор отсечения.

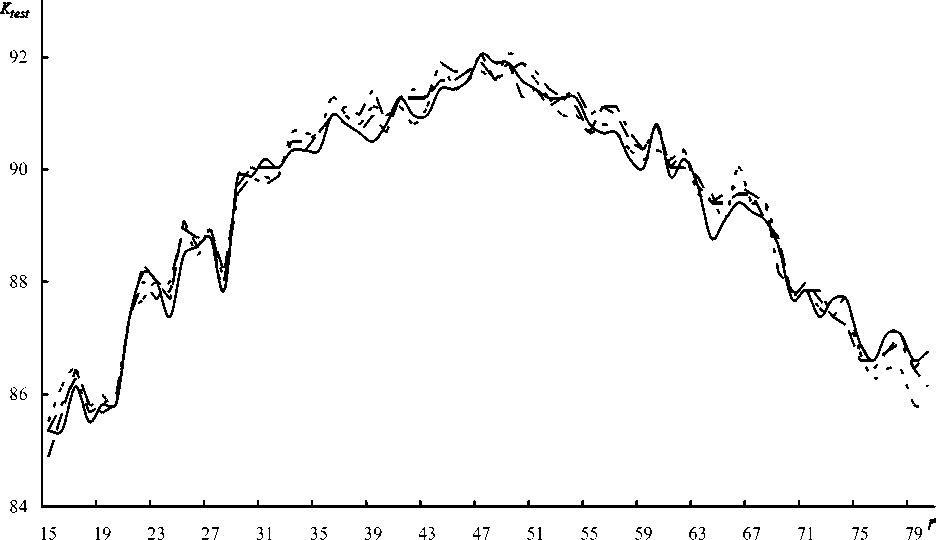
Рис. 3. Зависимость коэффициента распознавания тестового набора от числа дискриминантных компонент: метод Хаусхолдера ( сплошная линия), линейная конденсация ( CF = 1,5 – пунктирная линия; CF =2 – штрихпунктирная линия; CF =2,5 – штриховая линия )

Как видно из рис. 3, использование метода линейной конденсации для вычисления главных компонент не приводит к снижению точности распознавания.

Для демонстрации эффективности разработанной процедуры диагонализации вычисляются главные компоненты набора, состоящего из 1731 изображения, с использованием блоков различных размеров. Размеры блока диагонализации ( L ) варьировались от 50 до 600. Время вычисления главных компонент сравнивается с временем расчета главных компонент методом Хаусхолдера. Рис. 4 показывает относительное время T = Tc /T для вычисления 167 главных компонент в зависимости от размера блока диагонализации L . Здесь T_c – время вычисления главных компонент методом линейной конденсации, T_h – время для вычисления главных компонент методом Хаусхолдера.

Как видно из рис. 4, увеличение размера блока диагонализации способствует уменьшению времени расчета главных компонент, но только до определенных пределов. После того, как размер блока диагонализации превысил величину 350, относительное время вычисления начинает расти.

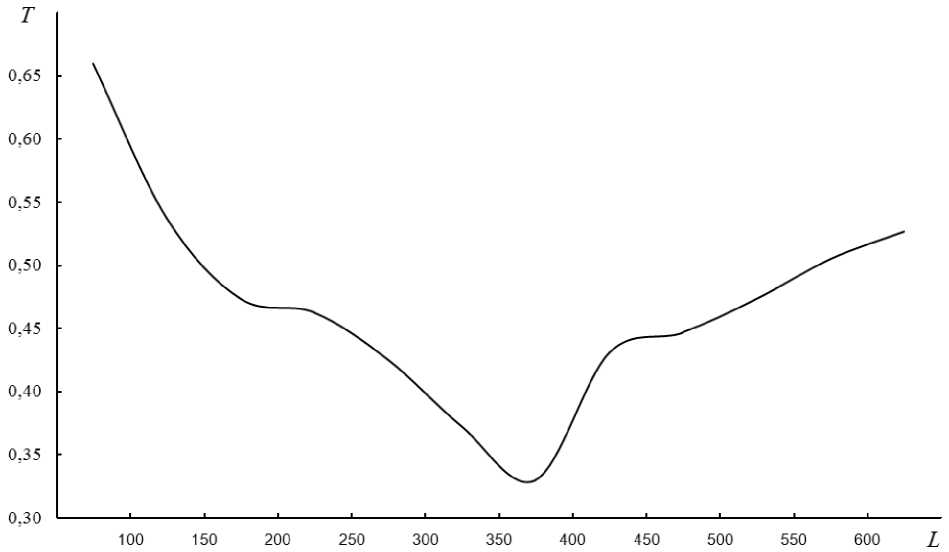
Рис. 4. Относительное время вычисления главных компонент в зависимости от размера блока диагонализации

Заключение

В статье рассмотрены некоторые аспекты использования метода главных компонент и линейного дискриминантного анализа для распознавания изображений. Основное внимание сосредоточено на вычислении главных компонент больших наборов изображений алгоритмом многоуровневой линейной конденсации. Алгоритм многоуровневой линейной конденсации использует аппроксимацию, позволяющую сократить порядок матриц с сохранением собственных значений в заданном диапазоне. Описана процедура блочной диагонализации матрицы, позволяющей повысить эффективность алгоритма. Демонстрация быстродействия разработанного алгоритма выполнена на примере обработки изображений базы данных FERET.