Об экономичном управлении нагревом металла в протяжных печах и агрегатах

В работах [1, 2] приведено достаточно скрупулезное обоснование принципа экономичного управления нагревом металла в печах. Реализация принципа обеспечивает такое распределение температуры по зонам, при котором достигается заданное качество нагрева, но при этом область наиболее высоких температур рабочего пространства смещается, насколько это возможно, к концу печи. За счет этого обеспечивается минимизация расхода топлива или электроэнергии на нагрев.

Принцип экономичного управления, как это отмечено в работе [2], поддается достаточно простому физическому осмыслению и объяснению. В самом деле, если основной нагрев – накопление основного количества теплоты – будет происходить в первых по ходу металла зонах печи, то во всех последующих зонах необходимо будет поддерживать высокие температуры рабочего пространства, так как качество нагрева должно быть заданным и допустить остывание металла нельзя. Понятно, что при такой ситуации вырастут удельные потери теплоты через кладку печей, а в топливных печах степень утилизации теплоты продуктов сгорания в пределах самой печи при прочих равных условиях существенно уменьшится.

Разумеется, что здесь речь идет о тех случаях, когда заданное время нагрева существенно больше времени максимального быстродействия. В задаче же максимального быст- родействия, очевидно, нет никакой свободы в выборе характера распределения тепловой нагрузки по зонам печи, понятно, что все отапливаемые зоны должны быть максимально нагружены. Естественно, что при этом степень утилизации теплоты, содержащейся в продуктах сгорания, в пределах топливной печи будет заметно меньше, чем в тех случаях, когда нагружены только последние по ходу металла зоны. Поэтому если сравнивать по экономичности режимы нагрева между собой, то для проходных и протяжных топливных печей режим максимального быстродействия может и не быть самым экономичным по расходу топлива.

Постановка задачи

Реализация указанной в работах [1, 2] закономерности оптимального процесса означает, по существу, адаптацию уровня температуры рабочего пространства в зонах к характеристикам нагреваемого металла и производительности печи. Применим эту закономерность для расчета экономичного распределения температуры по зонам горизонтальных протяжных печей (топливных и электропечей сопротивления) и агрегатов, используемых в метизной промышленности при термообработке проволоки и ленты. Дело в том, что сортамент нагреваемого металла и скорость его протяжки через такие печи и агрегаты изменяются сравнительно редко (в отличие от режима работы, например, методических пе- чей для нагрева слябов), вследствие этого здесь имеются более благоприятные условия для реализации оптимального управления, для наиболее полного использования преимуществ экономичного режима нагрева. Можно сказать, что характер работы протяжных печей метизной отрасли является в достаточной мере идеальным по отношению к методическим печам. Кроме того, математическое описание процесса нагрева термически тонких изделий существенно проще, что также облегчает задачу разработки алгоритма управления.

Разработка алгоритма расчета распределения температуры по зонам

Применяемые в метизной промышленности многозонные протяжные печи с косвенным обогревом металла (топливные печи и электрические печи сопротивления) [3, 4], как правило, оснащены локальными системами автоматического регулирования (САР) температуры рабочего пространства в зонах. При изменении режима работы печей локальные регуляторы автоматически вычисляют расход топлива или электрической энергии, требуемый для обеспечения заданного значения температуры рабочего пространства. Однако адаптация расхода топлива или электроэнергии к изменению режима работы печей, как показали исследования, является недостаточной. Для экономичного управления процессом нагрева необходимо ещё изменять и уровень самой температуры рабочего пространства в зонах печи, т. е. уставки локальных регуляторов температуры. Зачастую эта операция осуществляется обслуживающим персоналом вручную. Адаптация к изменяющимся условиям работы печей производится сравнительно редко и в очень ограниченном объёме. Обычно в зонах поддерживается избыточный уровень температуры рабочего пространства, обеспечивающий быстрый нагрев металла в первых зонах печей и, по существу, его выдержку в остальных зонах. Такой характер распределения температуры рабочего пространства по зонам гарантирует удовлетворительный нагрев металла в достаточно широком диапазоне изменения скоростей протяжки металла и его геометрических размеров. Вместе с тем внедрение современных систем управления температурным режимом на базе микропроцессорной техники позволяет дифференцированно управлять температурой ра- бочего пространства в зонах в зависимости от производительности печей и характеристик нагреваемого металла. При этом если, например, использовать принцип экономичного управления, то может быть получена значительная экономия топлива или электроэнергии при обеспечении качественного нагрева металла. Так, как это указано в работе [5], за счет реализации принципа экономичного управления был получен существенный экономический эффект – снижение расхода электроэнергии на нагрев проволоки в протяжных горизонтальных электропечах сопротивления составило 20 %. Имеются и другие данные о существенной эффективности применения принципа [1, 2, 6–9].

Таким образом, внедрение в практику эксплуатации печей принципа экономичного управления представляется весьма разумным подходом. В связи с этим рассмотрим реализующий этот принцип алгоритм расчета распределения температуры по зонам протяжной печи. Алгоритм расчета заключается в следующем.

Известно [10–12], что динамику нагрева металлоизделий типа проволоки и ленты в зоне i n -зонной протяжной печи можно описать следующей моделью:

( d^(L) = ^[ (_L)] _L^

) dL vTtL 3i 4 1 (1) ( t(0) = t*, где t(L) - температура металла в точке L по длине зоны; Li - длина зоны i; v - скорость протяжки металла через печь; Т - некоторая эквивалентная постоянная времени, определяемая при идентификации модели (1) для данной зоны и данного сортамента металла; t3i - температура рабочего пространства в зоне i; tHj - температура металла в начале зоны i, понятно, что она равна температуре металла в конце зоны (i — 1). Причем t3j должна удовлетворять следующему неравенству:

t '. ■ <  t ,i < t“ (2) где t “ⁱⁿ и t ™^ax - минимально и максимально допустимые температуры в зонах.

Используя решение дифференциального уравнения (1) при t₃ j = const, нетрудно показать, что температура металла в начале зоны i - t_H j , температура металла в конце зоны i - t_K j и температура рабочего пространства в зоне i - t₃ j связаны соотношением

tki = t3i + (tHi — t3i) ’ exp (—77)- (3)

и 1[/

Расчет распределения температуры по зонам n -зонной протяжной печи начинаем с зо-

ны п, при этом считаем, исходя из принципа экономичного управления, что температура в последней зоне печи - п поддерживается на максимально допустимом уровне - t ^^ax . Из технологической инструкции определяем требуемую температуру металла на выходе из печи - t_Kn . Зная скорость протяжки металла - п, параметр Т_п для последней зоны печи и дан-

ного сортамента нагреваемого металла, величины t ^^ax и L_n, из (3) находим температуру, которую должен иметь металл на входе в зону п - t_Hn , или что то же самое, температуру на выходе из зоны (п — 1) - t_K ( _n-1 ) , так как ^ к(п-1) = tm^.

допустимом уровне - t ™ⁱⁿ , i = 1, (п — 1). Обозначим эту температуру как t™ ⁿ .

Заметим, что расчет t ™ⁱⁿ , i = 1, (п — 1) нужно выполнить только один раз – при расчете температурного режима зоны п, а далее следует использовать полученные данные при расчете температурного режима всех предшествующих зон. Это обстоятельство в целом сокращает объем вычислительной работы.

Если t™ ⁿ > t_Hn, то для нагрева металла до требуемой по технологической инструкции температуры температуру рабочего пространства в зоне п следует снизить. Необходимая температура в зоне, очевидно, будет определяться из соотношения

^ кп ¹

tm =

Ц^1-е^хр(-^ _ )] ^ехр(^-^

.

^ кп

^ зп =

-^•ехр(-^)

^1-ехр(^-^   .

Далее, сравниваем t_K ( _n-1 ) = tm с температурой, которую будет иметь металл на вхо-

Расчет температурного режима печи в данном случае будет закончен – в последней

де в зону п при условии, что во всех предыдущих зонах температура рабочего пространства будет поддерживаться на минимально

зоне локальными регуляторами должна поддерживаться температура, определяемая по уравнению (5), а во всех предыдущих – на

минимально допустимом уровне.

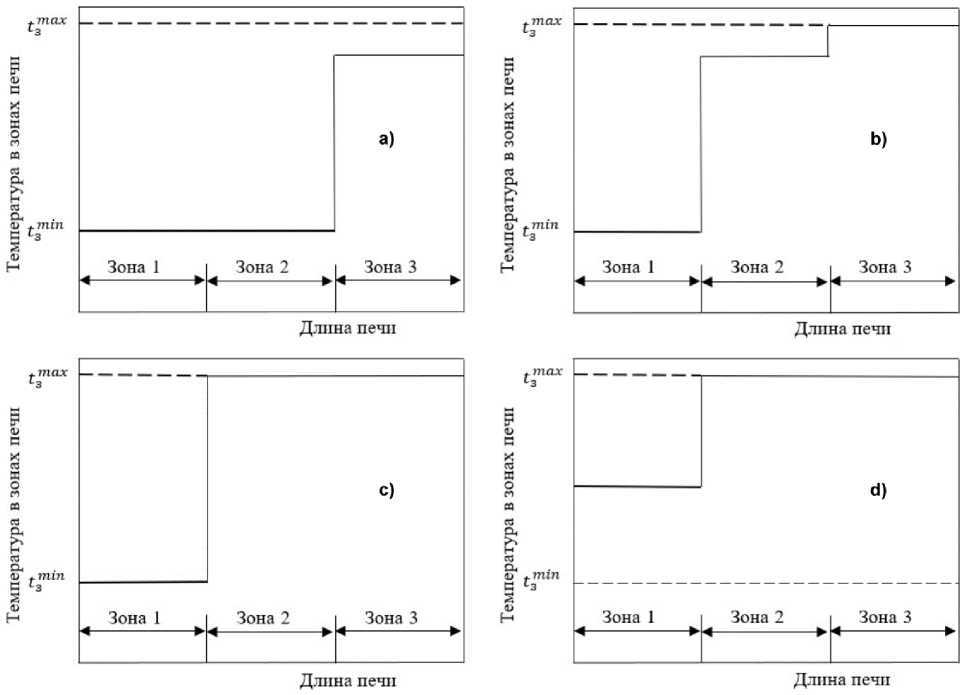
Рис. 1. Графики распределения температуры рабочего пространства по зонам трехзонной протяжной печи Fig. 1. Graphs of temperature distribution of the working space by zones of a three-zone broaching furnace

Если же t™ ⁿ = t_Hn, то в последней зоне должна поддерживаться максимально допустимая температура рабочего пространства, а во всех предыдущих – на минимально допустимом уровне.

При tH^ <  t_Hn считаем, что в зоне температуру нужно поддерживать на уровне t₃ “^ax и переходим к расчету температурного режима в зоне (п — 1), алгоритм расчета аналогичен расчету температурного режима зоны п.

На рис. 1 приведены получаемые по изложенному алгоритму графики распределения температуры рабочего пространства по зонам трехзонной протяжной печи для нагрева проволоки перед горячим оцинкованием. При этом следует иметь в виду, что в направлении от рис. 1а к рис. 1d производительность печи возрастает. Кроме того, здесь полагается, что минимально и максимально допустимые температуры одинаковы для всех зон.

Как это видно из рис. 1, при таком управлении печами отчетливо прослеживается реализация принципа экономичного управления – интенсифицировать нагрев только в последних по ходу металла зонах печи.

Для примера приведем результаты расчета экономичного распределения температуры рабочего пространства по зонам трехзонной печи длиной 26 м. В печи обрабатывается стальная проволока диаметром 2,4 мм, скорость протяжки при этом составляет 24 м/мин. Для данной печи t “ⁱⁿ = 300 °C,i = 1,3; t₃ "?^ax = 1100 °C, i = 13; F i = 17 с; T₂ = 20 с; T₃ = 20 с. Кроме того, температура металла на входе в печь составляет t_H1 = 20 °C, его конечная температура должна быть равна t_K 3 = 950 °C. В результате расчета установлено, что в соответствии с принципом экономичного управления температура рабочего пространства в первой зоне должна быть равна t₃₁ = t ™ⁱⁿ = 300 °C; во второй зоне -t₃₂ = 1009 °C, а в третьей - t₃₃ = t “^ax = = 1100 °C. При этом температура проволоки в конце первой зоны будет равна t_K1 = 221,7 °C, а в конце второй зоны - t_K2 = 743,2 °C.

При расчете конкретного режима нагрева может оказаться так, что при максимально допустимых температурах во всех зонах печи не обеспечивается нагрев металла до требуемой по технологии температуры, в этом случае в системе управления необходимо предусмотреть выдачу сообщения о необходимости уменьшения скорости протяжки металла через печь.

Заметим также, что если по требованиям технологии в некоторых зонах печей необходима выдержка металла при определенной температуре рабочего пространства, то при расчете распределения температуры величины t “ⁱⁿ и t ™^ax для данных зон следует положить равными температуре выдержки металла.

Вариант алгоритма для топливных печей с зоной предварительного подогрева

Необходимо заметить, что описанный алгоритм применим для горизонтальных электропечей сопротивления и топливных печей без зоны предварительного подогрева. Если у топливных печей такая зона имеется, то расчет требует следующей корректировки.

Предполагается, что температура рабочего пространства по длине зоны предварительного подогрева равномерно растет от некоторой температуры tc до температуры второй зоны t32, стабилизируемой собственным локальным автоматическим регулятором. В этом случае зависимость температуры рабочего пространства от длины вдоль этой зоны будет представляться следующим уравнением:

t3iG0 = tc+ ^^с-А, 0 < А < Л1.     (6)

^L 1

Как видно из соотношения (6), распределение температуры по длине зоны предварительного подогрева 1 однозначно определяется температурой зоны 2. Поэтому расчет температурного режима первой зоны – зоны предварительного подогрева – и второй зоны необходимо проводить совместно – в едином блоке, когда отыскивается или задается только температура металла на входе зоны предварительного подогрева и его температура на выходе из второй зоны, а также только температура рабочего пространства второй зоны.

Решая уравнение (1) для случая, когда температура рабочего пространства в пределах зоны предварительного подогрева изменяется по соотношению (6), найдем, что температура в конце этой зоны может быть вычислена по следующей формуле:

t(A1) = t32 + (tH1 — tc) • exp (— ^т) —

X VI1/

rT1^M1 — exp(—-M.         (7)

^ 1                        VI i

Поэтому температура металла в конце зоны 2 будет определяться по уравнению

tk2 = t32 + {(Сн1 — tc) exp (— Vr) —

—^1^[1—exp(—£)]}«* (—;V (8)

Данное соотношение используется как при определении t ^ⁱⁿ - температуры металла на входе зоны 3 при поддержании температуры рабочего пространства зоны 2 на минимально допустимом уровне - С_з^ ^п , так и при вычислении необходимой температуры рабочего пространства в зоне 2, обеспечивающей необходимое значение температуры металла на входе в зону 3 - t_H3. Необходимое для этого соотношение имеет вид:

t H ₃4t Hi -t c )exp[4(^+g)]-vt_c^[l^^

t₃ 2 ^—------------- , Тф ² / чм ------------ .                                       ⁽⁹⁾

^l-v z1 ^[l-exp(^- ^i^ )^]exp(^-;^)

При решении данной задачи можно применить подход работы [2] – вместо задания температуры t_c считать, что температура рабочего пространства в зоне предварительного подогрева линейно увеличивается по ее длине с коэффициентом к до температуры во второй зоне печи. В этом случае температура рабочего пространства по длине этой зоны будет вычисляться по формуле

t3i(L) —t32-k(Li-L),0

Реализация на агрегатах с ЭКН

Применяемые на АО «БМК» (Белорецкий металлургический комбинат) протяжные агрегаты с электроконтактным нагревом проволоки (ЭКН) представляют собой, по существу, протяжные печи-агрегаты, алгоритм расчета управляющего воздействия для которых является частным случаем вышеизложенного алгоритма – в любом случае нужна адаптация режима работы как к производительности агрегата, так и к сортаменту нагреваемого металла. Здесь только следует иметь в виду, что вид функциональной зависимости типа (1) несколько иной [13–15] и управляющим воздействием является не температура зоны, а действующее значение напряжения на данном участке нагрева.

Систему управления протяжными термоагрегатами с ЭКН на АО «БМК» реализовали на базе микропроцессорного контроллера Ремиконт [9, 15]. При этом весь сортамент термообрабатываемой на данных агрегатах проволоки разбивали на группы, для вычисления действующего значения напряжения, необходимого для нагрева проволоки данной группы до требуемой температуры, использовали алгоблоки с алгоритмами кусочно-линейной аппроксимации. Алгоблоки других групп при работе на данном сортаменте находятся в отключенном состоянии.

Система управления осуществляет автоматическую адаптацию управляющего воздействия – напряжения нагрева к скорости протяжки проволоки через агрегат, адаптация к характеристикам нагреваемого металла осуществлялась обслуживающим персоналом вручную путем выбора соответствующего положения переключателя сортамента проволоки.

Промышленная эксплуатация системы показала, что существенно повысилась точность нагрева, что привело к улучшению сортности проволоки, увеличилась производительность агрегатов, а расход электроэнергии снизился. При этом также нужно иметь в виду, что повышение точности нагрева приводит, в конечном счете, и к уменьшению удельного расхода топлива или электроэнергии на нагрев [16].

Некоторые замечания к решению задачи параметрической идентификации модели

Постоянные времени Tj, i — 1, и следует определять посредством решения задачи параметрической идентификации модели (1) по экспериментальным данным. Процедуры решения таких задач достаточно хорошо известны [17]. Здесь разумно рекомендовать подход работы [18] и использовать для решения задачи результаты измерения температуры металла на выходе из n-зонной протяжной печи. Обусловлено это тем, что измерение температуры движущегося металла в протяжных печах либо практически невозможно (например, в муфельных печах), либо не целесообразно из-за сложности реализации, существенного влияния на результат ряда факторов, как то печной атмосферы, меняющей свое значение степени черноты металла, фонового излучения кладки и т. п. В качестве критерия идентификации предпочтительнее брать модульный критерий

J(T1, T2, ■ , Tn) — 2т=1ккп,т

-

t р I ^ кп,т|,

р где tKn,rn и Скп,т — экспериментальное и расчетное значение температуры проволоки на выходе n-зонной протяжной печи; m - номер эксперимента. При этом, как это нетрудно видеть, расчетное значение температуры следует вычислять, например, для четырехзонной печи (без зоны предварительного подогрева) по соотношению

t« = 4» + {Из + Iел + [41+ (tHi - 41) • exp (-;^) - 41] х

х е!р(-Й - 'М • exp (-;й;)} - '=’■>> • exp (-;У.                               (12)

Здесь tfj, i = 1,4 - реальные значения температуры рабочего пространства в зонах печи при проведении эксперимента для идентификации.

Понятно, что в данном случае мы имеем дело с задачей нелинейного программирования – с задачей минимизации критерия (11) посредством выбора численных значений постоянных времени Tj, i = 1,4. Как показано в работе [18], эта задача вполне удовлетворительно решается методом конфигураций (Хука и Дживса).

Выводы

Разработан алгоритм расчета распределения температуры по зонам протяжных печей и агрегатов. Алгоритм реализует принцип экономичного управления нагревом металла в печах и обеспечивает адаптацию уровня температуры рабочего пространства в зонах к характеристикам нагреваемого металла и производительности печи. Варианты алгоритма применимы как для печей без зоны предварительного подогрева, так и для печей с наличием такой зоны. Указано, что с использованием соответствующих функциональных зависимостей алгоритм применим и для протяжных термоагрегатов с электроконтакным нагревом проволоки. Приведены рекомендации по решению задачи параметрической идентификации, используемой в составе алгоритма модели нагрева.