Об экспериментальной идентификации нелинейного динамического поведения конструкции малого космического аппарата

Как известно, не существует конструкций, динамическое поведение которых линейно, но принято исследовать такие конструкции, за исключением крупногабаритных трансформируемых конструкций [1-3], используя принцип линеаризации. Так, T.K. Caughey в своих основополагающих статьях [4-6] предложил заменить нелинейный осциллятор с внешним гауссовым возбуждением на линейное с таким же возбуждением, что среднеквадратичная ошибка между реальными нелинейными и линеаризованными системами сводится к минимуму в статистическом смысле. В литературе его часто связывают с методом статистической линеаризации, введенным Казаковым [7].

В связи с постоянным интересом к расширению диапазона характеристик конструкций космических аппаратов при одновременном сокращении их экспериментальной наземной отработке, существует необходимость в проек-

Филипов Александр Геннадьевич, аспирант.

Баляба Максим Владимирович, кандидат технических наук, инженер учебной лаборатории пневмогидравлических систем.

Глазков Игорь Евгеньевич, аспирант.

тировании более лёгких, сложных и, как следствие, более нелинейных конструкций. Поэтому довольно противоречиво наблюдать, что при анализе таких конструкций не учитываются их нелинейное динамическое поведение. Действительно, основные принципы, применимые к линейным динамическим системам и составляющие основу модального анализа, больше не действуют при обнаружении нелинейности в поведении конструкции.

Любой космический аппарат и его системы подвергаются динамическим нагрузкам как при запуске, так и на орбитальном участке полёта. Для обеспечения безаварийного выведения и штатной работы аппаратуры на всём сроке эксплуатации космического аппарата, необходимо получить как можно более достоверную математическую конечно-элементную модель объекта исследования. Это позволит наиболее точно оценить действующие на него нагрузки и степень влияния нелинейности на его динамические характеристики.

В работах авторов [8-12] проведены исследования по выявлению нелинейного динамического поведения. Так, например, K. Carney [10] проводил анализ нелинейности динамического поведения космического аппарата CASSINI. Он выяснил, что опоры фермы, которые используются на Cassini, могут вызвать нелинейность из-за сложности устранения зазоров и при попытке протестировать структуры с этим классом нелинейности важно иметь возможность возбуж- дать исследуемый образец до высоких уровней отклика. K. Carney пришёл к выводу, что можно определить истинный отклик конструкции на критических уровнях и, возможно, линеаризовать его.

Однако, ввиду высшей степени «индивидуалистического» характера нелинейных систем, не существует общего метода их анализа, который можно было бы применить во всех случаях, как при модальном анализе [13].

МЕТОД ИССЛЕДОВАНИЯ

Объектом исследования в данной статье является динамическое поведение малого космического аппарата дистанционного зондирования земли (МКА). Динамический макет МКА был закреплен на испытательную оснастку (см. рис. 1), в соответствии с граничными условиями его выведения с помощью ракеты-носителя.

На начальном этапе исследования был проведён эксперимент по выявлению нелинейного динамического поведения методом прямого и обратного сканирования амплитудно-частотных характеристик (АЧХ), но каких-либо адекватных результатов получить не удалось. То есть, смещение полученных резонансных частот между прямым и обратным сканированием не было выявлено (см. рис. 2).

Для исследования нелинейности в динамическом поведении МКА были выбраны некоторые его элементы (бортовая аппаратура и корпус телескопа). Схемы расположения датчиков на МКА приведены на рисунках 3, 4, где позиции указывают на места установки датчиков. В скобках указаны места их установки с противоположной стороны МКА.

В ходе эксперимента были проведены замеры при возбуждении МКА вдоль горизонтально оси Z.

Предварительно были определены АЧХ испытательной оснастки с целью обнаружения её влияния на результаты эксперимента в диапазоне частот до 100 Гц.

Испытательные режимы для определения нелинейного характера поведения задавались в соответствии с резонансными частотами, полученными при выявлении АЧХ МКА (см. рисунок 2). Резонансные частоты исследуемого объекта были определены в соответствии с методом, описанным в предыдущей работе автора [14]. На каждой резонансной частоте задавались уровни в соответствии с таблицей 1.

РЕЗУЛЬТАТЫ

По завершению испытаний по режимам таблицы 1 были получены результаты, приведенные в таблице 2 и рисунке 5-8. В таблице и на

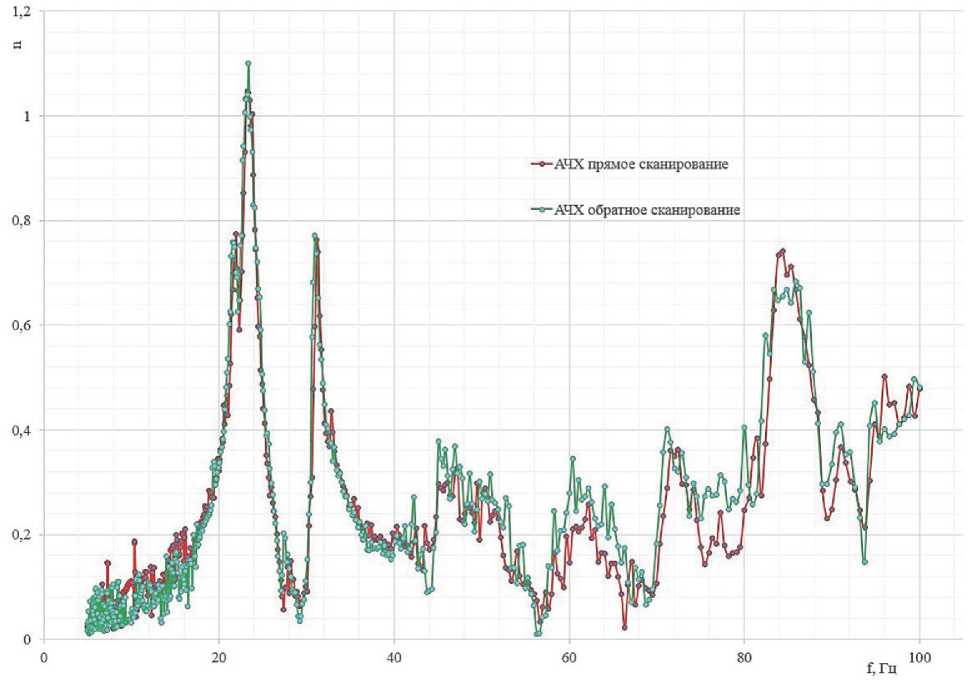
Рисунок 2 – АЧХ МКА при прямом и обратном сканировании

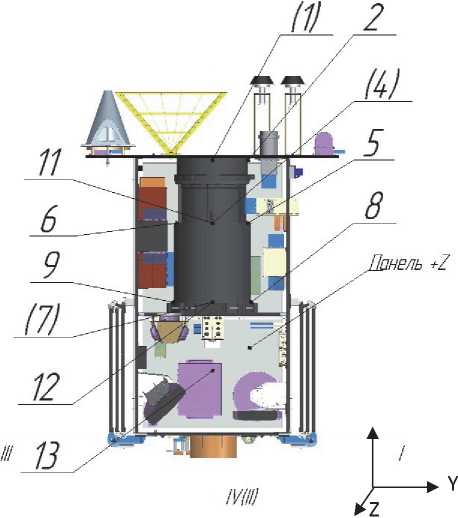
Рисунок 3 – Схема расположения датчиков на элементах МКА рисунках 5-8 приведены значения отклика в ускорениях (мм/с2) по датчикам, имеющим заметные результаты.

Как видно из таблицы 2, на частотах 30 и 32 Гц в местах установки датчиков на сотопанели и

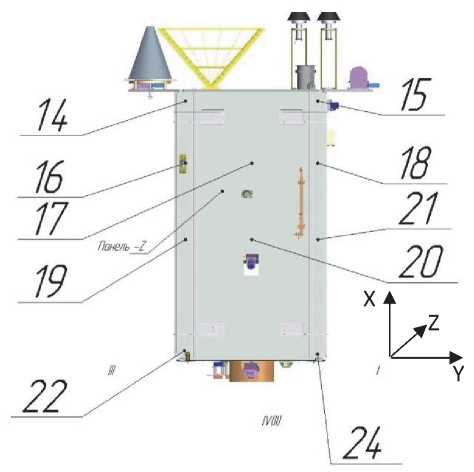
Рисунок 4 – Схема размещения датчиков снаружи на МКА (на панели –Z)

нижней части рамы конструкции МКА мы получили явный нелинейный отклик конструкции, которая имеет локальный характер. Данные эксперимента по другим частотам и местам установки датчиков имеют более линейную картину динамического поведения. Учитывая результаты сканирования АЧХ (прямое и обратное), а

Таблица 1 – Режимы определения нелинейности конструкции

Внутри КА (на телескопе)
Резонансные частоты, Hz	Уровни нагружения, g
15.5	0.1	0.2	0.3	0.4	0.5	0.8
29	0.1	0.2	0.3	0.4	0.5	0.8
С внешней стороны на раме КА
Резонансные частоты, Hz	Уровни нагружения, g
10	0.1	0.2	0.4	0.8	-	-
21	0,1	0,2	0,4	-	-	-
23	0,1	0,2	0,4	-	-	-
30	0,1	0,2	0,3	0,4	0,8	-
32	0,1	0,2	0,3	0,4	0,8	-

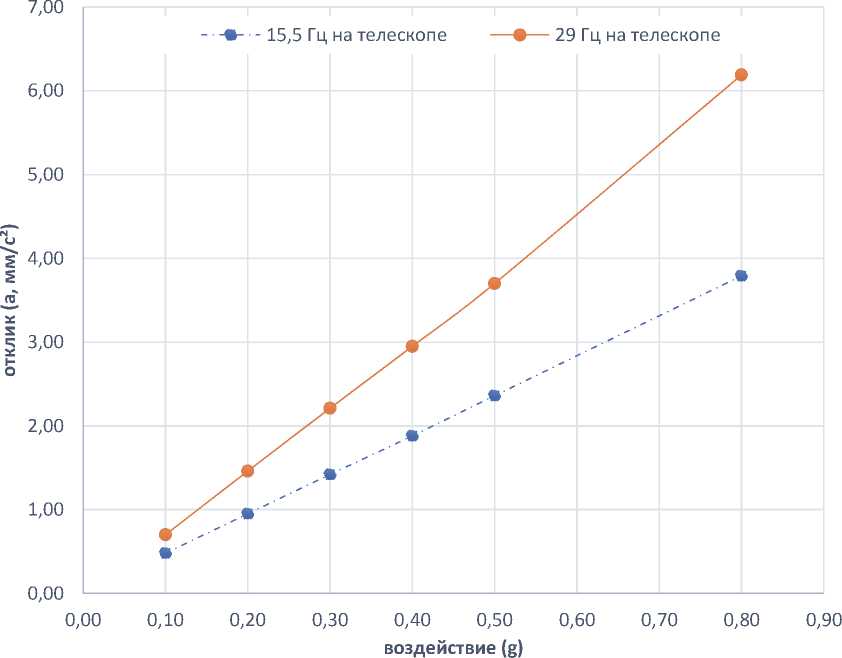
Рисунок 5 – Результаты испытаний внутри МКА (телескоп)

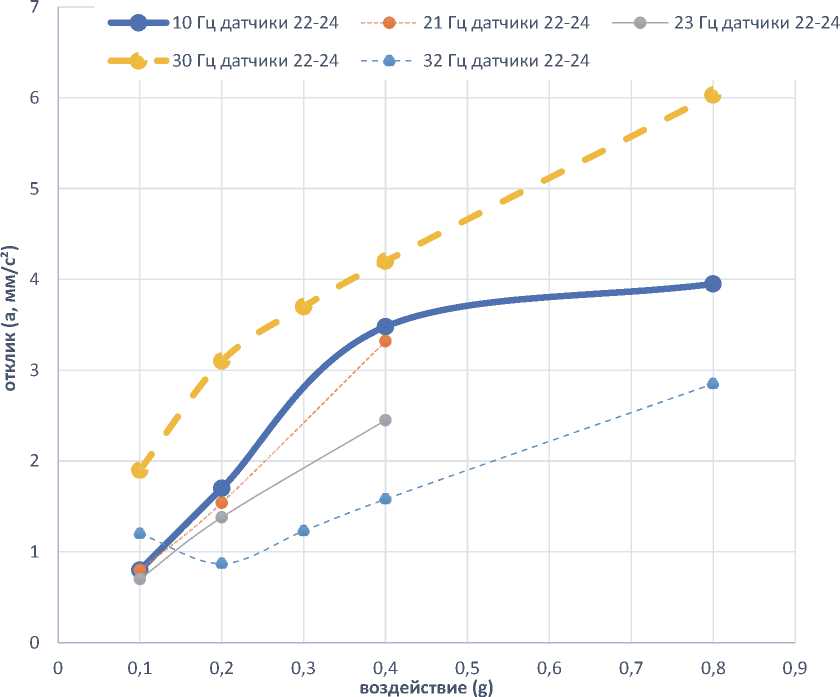
Рисунок 6 – Результаты испытаний у основания МКА (рама)

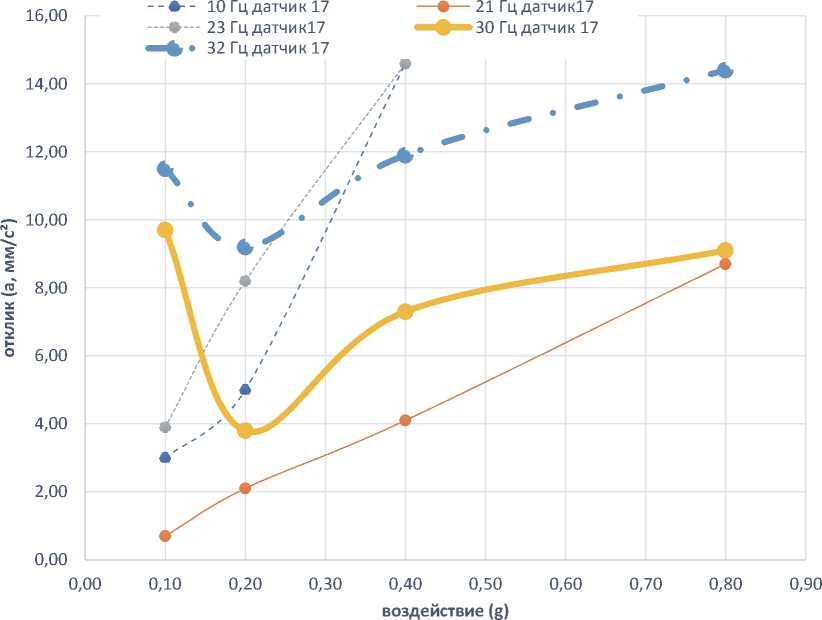
Рисунок 7 – Результаты испытаний на оболочке МКА (сотопанель)

воздействие (g)

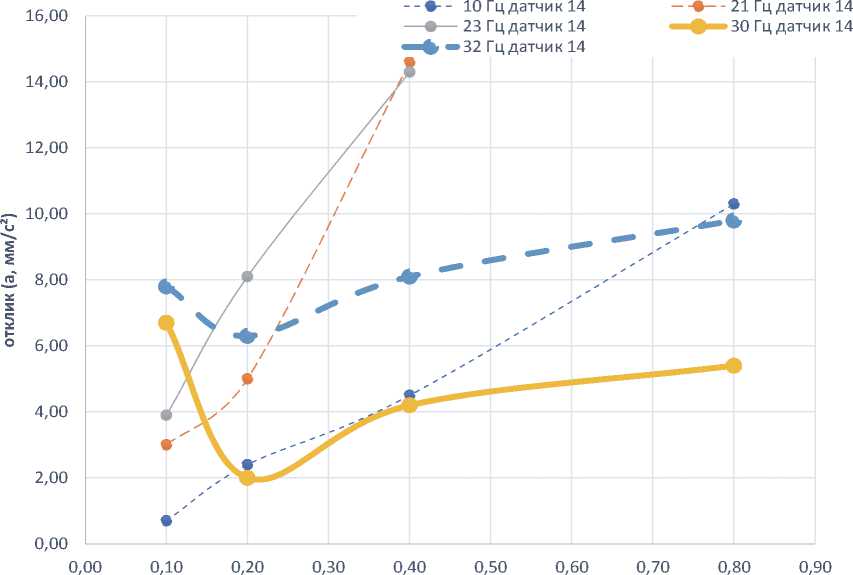
Рисунок 8 - Результаты испытаний на верхней части МКА (рама)

Таблица 2 - Результаты испытаний (значения перегрузок)

Внутри КА (на телескопе) Частоты, Hz Уровни нагружения, g 0,1 0,2 0,3 0,4 0,5 0,8 Отклик конструкции, а, мм/с2 15.5 0,48 0,95 1,42 1,88 2,36 3,79 29 0,7 1,46 2,21 2,95 3,7 6,19 С внешней стороны на раме КА (у основания КА) 10 0,8 1,7 3,48 3,95 21 0,8 1,54 3,32 23 0,7 1,38 2,45 30 1,9 3,1 3,7 4,2 6,03 32 1,2 0,87 1,23 1,58 2,85 С внешней стороны на сотопанели КА 10 0,7 2,1 4,1 8,7 21 3 5 14,6 23 3,9 8,2 14,6 30 9,7 3,8 7,3 9,1 27,4 32 11,5 9,2 11,9 14,4 23,2 С внешней стороны на раме КА (в верхней части КА) 10 0,7 2,4 4,5 10,3 21 3 5 14,6 23 3,9 8,1 14,3 30 6,7 2 4,2 5,4 18,4 32 7,8 6,3 8,1 9,8 15,7 также результаты таблицы 2, можно сделать выводы, что динамическое поведение конструкции описывает локальную нелинейность материалов конструкции.

Уравнение движения модели в данном случае примет вид:

M x (t, 0) + C x (t, 0) + Kx((t, 0) +

+f„l (x(t, 0), X(t, 0), 0) = f(t), где M, C, K ERNxN - матрицы массы, демпфирования и жесткости, соответственно. f(t) GRNx1 - внешнее возбуждение. X(t, 6), X(t, 6), x((t, 6) ERNx1 - векторы ускорения, скорости и перемещение, соответственно. fni (x(t, 6), Ш 6), 6) еRNx1 - нелинейная восстанавливающая сила.

Стоит отметить, что нелинейное динамическое поведение мы наблюдаем на резонансных частотах, очень близких друг к другу. Можно предположить, что это связано с явлением нелинейного биения, при которых две или более соизмеримых линеаризованных частоты обмениваются энергией между собой [15].

При расчёте динамических нагрузок необходимо будет учесть данные результаты путём коррекции матрицы демпфирования для определённых элементов конструкции.

ВЫВОДЫ

При анализе полученных результатов можно наблюдать, что отклики конструкции на разные уровни нагружения имеют нелинейный характер. Вероятно, это связано с диссипативными характеристиками конструкции и в данном случае имеет чисто локальный характер. Это и нужно выяснить на следующем этапе исследования.

По результатам исследования данного этапа работ можно сделать предварительный вывод о том, что явное нелинейное поведение не характерно для конструкций, имеющих малые габариты, как в случае с бортовой аппаратурой, и жесткую конструкцию - в случае с корпусом объектива.