Об экспоненциальной модели нагрева слябов в методических печах

Постановка задачи

Известно, что удовлетворение современных требований к автоматизации нагревательных печей прокатного производства возможно только в рамках систем управления с обратной связью по температуре нагреваемого металла [1–3]. При этом следует иметь в виду, что при нагреве слябов в методических печах для непосредственного измерения доступна лишь температура их поверхности. Температура внутренних точек, так же как и среднемассовая (среднеобъемная) температура, не может быть принципиально измерена инструментальными средствами. Определяются они расчетным путем, либо напрямую по математической модели, либо по разработанным на ее основе алгоритмам контроля [4–6].

В литературе известно большое количество работ, посвященных моделированию и алгоритмизации процесса нагрева, расчету температурных полей нагреваемых заготовок [см., например, 1–8], однако безупречного решения проблемы до сих пор нет, требуются дальнейшие исследования и проработки, в частности, задачи выбора приемлемой структуры математической модели. Обуславливается это во многом тем, что температурные поля заготовок при нагреве в печах характеризуются наличием чрезвычайно большого количества особенностей, причем их детальный учет возможен только в рамках достаточно сложных структур моделей, а это при создании АСУ ТП и нереально, да и нецелесообразно, поскольку система должна работать в режиме реального времени, а требуемая вычислительная мощность УВМ не должна быть слишком большой. Кроме того, должная отработка (должное предотвращение) всех нежелательных особенностей температурных полей заготовок практически невозможна, да и не является абсолютно необходимой. Для этого потребуется серьезное усложнение как самой системы обогрева металла, так и технической и, естественно, алгоритмической структур АСУ ТП. Для управления технологическим процессом достаточно иметь некий интегральный показатель качества нагрева (температурного поля), в качестве такового часто используется так называемая среднемассовая температура металла. Для ее расчета в ряде случаев достаточно успешно применяют так называемые экспоненциальные зависимости (модели) [9–11]. Причем полагается, что процесс нагрева условно разбит на n участков, на каждом из которых параметры модели имеют свои собственные численные значения. Считается, что таким образом (с помощью кусочно-постоянной аппроксимации параметров) учитываются сложные нелинейные процессы внешнего и внутреннего теплообмена в печах. Однако при этом подчеркивается, что экспоненциальная структура таких моделей выбрана в основном из эвристических соображений, связь с физикой процесса никак не отмечается, указывается на статистический характер этих зависимостей [10]. Вместе с тем интересно было бы знать, насколько экспоненциальные модели соответствуют физике процесса нагрева, какая точность описания при этом может быть достигнута. Ведь хорошо известно, что чем точнее модель соответствует физике явления, тем больше допустимый диапазон ее применимости (работы).

В данной работе показано, что экспоненциальные модели обуславливаются (с некоторой погрешностью) самой физикой процесса нагрева, описываемой дифференциальным уравнением теплопроводности. Также указывается достаточно простая схема перехода от параметров модели, ядром которой является дифференциальное уравнение теплопроводности, к параметрам упрощенной модели для среднемассовой температуры.

Решение задачи

Для решения поставленной задачи опишем процесс нагрева слябов в методических печах на рассматриваемом участке расчета полностью линеаризованным уравнением теплопроводности:

∂ t ( x , τ )     ∂ ² t ( x , τ )

=a        , 00(1)

∂τ∂ с начальным

t(x,0) =t0(x), 0≤ x≤L(2)

и граничными условиями:

∂t(0,τ) =0, τ≥0;(3)

∂ x

λ∂t(L,τ)=α[tП(τ)-t(L,τ)],τ≥0,(4)

∂x где t(x, τ) – температура в точке с пространст венной координатой x в момент времени τ ;

a и λ – соответственно коэффициенты тем- пературопроводности и теплопроводности; L – расчетная толщина заготовки, t0(x) – некоторая функция, описывающая начальное температурное поле заготовки; α – коэффициент теплоотдачи; tП(τ) – температура рабочего пространства печи.

Здесь полагается, что за счет разбиения процесса на n расчетных участков, на каждом из которых параметры указанной модели имеют свои собственные численные значения, удается должным образом учитывать сложные нелинейные процессы внешнего и внутреннего теплообмена в печах.

Отметим, что описание процесса в линеаризованной форме соответствует вышеупомянутой концепции кусочно-постоянной аппроксимации параметров при моделировании сложного нелинейного процесса нагрева.

Очевидно, что при одностороннем нагреве L равно действительной толщине сляба, а при симметричном нагреве L равно половине фактического сечения заготовки. Кроме того, как показано в работе [12], за счет выбора уставок (заданий) регуляторам температуры нижних зон при фактически несимметричном нагреве температурное поле заготовки можно тоже сделать симметричным, поэтому и в этих случаях под L следует понимать половину толщины сляба. Следует заметить, что результаты работы [12] можно рассматривать как теоретическую основу допустимости описания процесса в симметричной форме, это во многих случаях приводит к существенному упрощению решения задач – проблема выбора расчетной толщины заготовки автоматически снимается, а при оптимизации управления печами это позволяет в два раза уменьшить размерность искомого вектора управления.

Проинтегрируем уравнение (1) по координате x в пределах от 0 до L и разделим обе его части на L , тогда получим dt _ a d t(L, t) d t (0, t) d т  L   dx      dx

1L где t _ — jt(x, t)dx - среднее значение температуры заготовки (среднемассовая температура). L0

Подставим соотношения (3) и (4) в уравнение (5), тогда получим dt     а а г .        . . -1

_ - , [ t п ^{( т ) -} t ⁽ L , ^{т )} ]

d т X L

Описание нагрева металла с помощью экспоненциальных моделей означает, что дифференциальное уравнение процесса имеет вид d"^ = 9[ t п(т) - tF(T)], (7) где 9 -1 - некоторая постоянная времени, это единственный параметр экспоненциальной модели, который, как это понятно, должен быть определен по реальным данным. Здесь через tP (t) обозначено вычисляемое по экспоненциальной модели значение среднемассовой температуры металла.

Сравнивая вышеприведенные уравнения (6) и (7), нетрудно увидеть, что экспоненциальная модель полностью бы соответствовала физике процесса нагрева, если бы среднемассовая температура тела не отличалась от температуры его поверхности. Однако в реальных условиях это не так, поэтому для уменьшения погрешности расчета по модели (7) необходимо отыскивать опти- n                        а а “ мальное значение параметра 9, прямое приравнивание 9 _---, очевидно, годится только для

X L случая термически тонких тел (это когда температура поверхности t(L, т) тела равна его средне-

1L массовой температуре t _— jt(x, т) dx).

L ₀

Примем следующее начальное условие для дифференциального уравнения (7) 1L tP (0) _ — [ t0 (x, t) dx

Р _{L 0}

и проанализируем ошибку расчета среднемассовой температуры по модели (7), (8). Вычитая (7) из (6) с учетом начальных условий, получим, что ошибка расчета среднемассовой температуры 51 (t) _ t (t) - tP (t) удовлетворяет следующему дифференциальному уравнению первого порядка d5dT(T) _9[ф(t)-5t (t)]

с начальным условием

5 F (0) _ 0,

а а          а а где ф(т) _ (—- -1) tn (t) - -—t (L, t) + t (t).

X L 9         X L 9

Известно, что решение дифференциального уравнения (9) с начальным условием (10) представляется в виде

57 ( t ) _9 ехр( -9т ) j ехр( 9т ) ф ( t ) d t .                                                       (11)

Подставляя в уравнение (11) конкретное значение ф ( т ) , найдем, как изменяется ошибка расчета среднемассовой температуры. Понятно, что эта величина будет разной в различных случаях. Конечно, предварительно необходимо определить ф ( т ) для конкретного режима нагрева.

Решение уравнений (1)-(4) для произвольной функции t _П( т ), описывающей изменение температуры рабочего пространства печи во времени, известно [13]. Поэтому, используя это решение, найдем общее выражение для ф ( т ):

” С 2

ф ^(т) = Е)У   , ■

У [ L p i + sin p i • cos p i

p i

L

x

• [ t 0 ( x ) - t _n (0)] • cos p, — • dx —

₀         П           i_L

—

2sin p i

p i + sin p i • cos p i

т                        , X ■> sin p,—

•J exp( p 2  ) •     • _d Л _

0        L ²     d ^T

a a p,-------cos p,-

¹ X L 9       i

p i

. 2 a 7 exp^(—p i -^x

где p i ( i = 1,2,...) - корни уравнения -^^ = ctg p i . a L

При нагреве слябов в методических печах температура рабочего пространства в зонах обычно поддерживается на постоянном уровне, только в неуправляемой (неотапливаемой) методической зоне температура линейно растет к началу первой сварочной зоны. Поэтому прежде всего следует проанализировать особенности первого режима нагрева, возможность его описания экспоненциальной моделью.

Для этого режима нагрева установлено, что величина ошибки прямо пропорциональна разности начальной температуры металла и температуры рабочего пространства на данном участке расчета [14]. Эта характеристика (особенность) вполне понятна и объяснима, так как разность указанных температур прямо пропорциональна градиенту температурного поля на поверхности заготовки (см. уравнение (4)), а чем больше его величина, тем значительнее неравномерность температуры по ее сечению и тем сильнее среднемассовая температура заготовки отличается от температуры ее поверхности.

Далее, при нагреве при постоянной температуре рабочего пространства с увеличением времени среднемассовая температура обязательно приближается к температуре поверхности, поэтому величина ошибки тоже в пределе стремится к нулю, следовательно, для удаленных моментов времени описание нагрева с помощью экспоненциальных моделей становится более оправданным. А поэтому и наиболее рациональное значение параметра 9 в этом случае должно стремить- a a         a a _ ся к---, т. е. 9 ^ —. Однако для начальных моментов времени расчетного участка нагрева эта X L         X L разность температур, как правило, велика.

При t _П( т ) = t _п (0) = const и t ⁰( x ) = t ⁰ = const формула для определения ошибки расчета имеет вид

8 t ( т ) = 9 [ t ⁰

—

” t п(0)] Е ] i = 1

L ²

9 L ² — p ia

„ . _z .            a a

² sin p i (sin p i ^— p i — cos p i )           „ _T             )

------;-----:----^{X L 9}—--^[exp^(— p 2 -y)^— exp^(—9 t ^)] ) . ⁽¹³⁾

p i ( p i + sin p i • cos p i )                  L                J

Из формулы (13) отчетливо видно, что если бы 9=^^ для любого V i, то ошибка расчета была бы в точности равна нулю для любого момента времени и, следовательно, экспоненциальная модель абсолютно точно соответствовала бы физике процесса нагрева, описываемой дифференциальным уравнением теплопроводности. Однако это совершенно не возможно, параметр 9 не может быть равен одновременно различным числам. При этом, однако, выясняется, что при

9>

p ia

L ²

в формуле (13) слагаемое, соответствующее данному значению i , становится равным

нулю. Заметим, что при выяснении этого факта приходится по правилу Лопиталя раскрывать неопределенность вида 0/0 и учитывать соотношение ^i^ = ctg pi. Поэтому вполне очевидно, aL что за счет выбора числового значения параметра 9 следует обнулить самое большое слагаемое в сумме (13), а это, как известно, имеет место для i = 1 [15-17], т. е. разумно полагать, что

2 a                  , , о                           ^цХ

6 = ц1 — , где ц1 - первый корень уравнения = ctg ц, что в принципе согласуется с теорией La регулярного теплового режима [15–17], допускающей описание нагрева первым членом ряда, представляющего решение системы (1)–(4). Таким образом, настроенное на физику процесса нагрева уравнение (7) будет иметь вид d t (т)2

Р    =Н1Т2"[ t П(т)- tp(T) ],(14)

d т

Из уравнения (14) вытекает достаточно простой способ перехода от физической модели (1)–(4) к экспоненциальной модели (14) (или (7)): a и L определить по характеристикам заго- цХ товки, а ц найти из решения уравнения    = ctg ц. При этом, конечно, предварительно из ре-

1                                a L шения задачи параметрической идентификации модели (1)–(4) следует найти значение наиболее трудно определяемого коэффициента теплоотдачи a .

На рисунке приведены кривые изменения во времени первого слагаемого соотношения (13) (51(т) - кривая 1) и суммы всех остальных слагаемых (52 (т) - кривая 2) для относительной ошибки расчета 5t (т)/[t0 - tn (0)] при 6 = aa= 3,00 ч 1. Здесь рассматривался нагрев углероди-Х L стой заготовки с толщиной L = 0,1м при числе Био Bi = 1,5 . Заметим, что в данном случае наи- a

, при этом вся относительная

более рациональное значение параметра 6 = ц1 — = 1,95308 ч ошибка будет удовлетворять следующему неравенству: 5t (т) / [t0 -tП (0)] < 0,02. При разности начальной температуры металла и температуры печи на данном участке расчета в 1000 °С абсо лютная величина ошибки расчета в этом случае не будет превосходить 20 °С, что часто вполне приемлемо для практики [18–20].

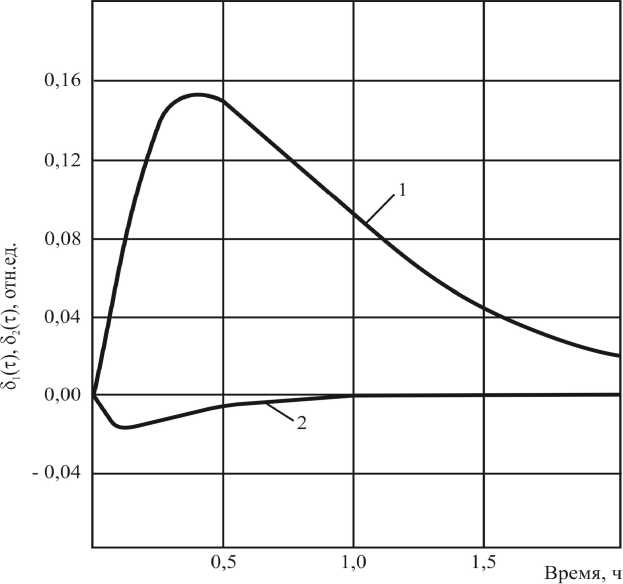
Изменение во времени первого слагаемого и суммы всех остальных слагаемых для относительной ошибки расчета

Как видно из рисунка, первое слагаемое действительно является основным по величине в сумме (13).

Далее отметим, что линейное изменение температуры рабочего пространства приводит к возникновению дополнительной по сравнению с 1-м режимом ошибки расчета, причем с увеличением времени она стремится к некоторому установившемуся значению, определяемому характеристиками системы. Если же температура рабочего пространства изменяется по экспоненте, то дополнительная ошибка расчета растет с течением времени уже неограниченно [14]. Таким образом, применение экспоненциальных моделей для случаев линейного и экспоненциального изменения тем-

пературы рабочего пространства вряд ли допустимо.

Выводы

Показано, что экспоненциальная модель нагрева слябов в методических печах обуславливается (с некоторой погрешностью) самой физикой процесса нагрева, описываемой дифференциальным уравнением теплопроводности. Указывается достаточно простая схема перехода от параметров модели, ядром которой является дифференциальное уравнение теплопроводности, к параметрам упрощенной модели для среднемассовой температуры. Результаты работы могут быть использованы при разработке и совершенствовании алгоритмического обеспечения АСУ ТП методических печей.